Cytogenetics

Cytogenetics is a study of structure, function, behavior and pathology of chromosomes.
Cytogenetics is a branch of genetics that is concerned with how the chromosomes relate to cell behaviour, particularly to their behaviour during mitosis and meiosis.[1]
Theoretical cytogenetics
[edit | edit source]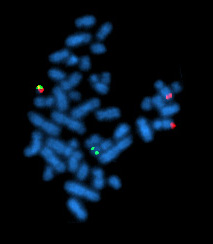
Def. the "branch of genetics that studies the relationships between the structure and number of chromosomes as seen in isolated cells and variation in genotype and phenotype"[2] is called cytogenetics.
Molecular cytogenetics
[edit | edit source]Molecular cytogenetics is a useful tool for the diagnosing and treatment of various malignancies such as brain tumors, haematological malignancies, etc.[3][4]
In Lilium longiflorum, Rad51 and Lim15 (an ortholog of Dmc1) co-localize on meiotic prophase I chromosomes where they form discrete foci.[5]
Rad51 and/or Lim15 proteins are components of early meiotic nodules that are involved in recombination related events.[6]
The stages of meiosis in which the co-localization of the Rad51 and Lim15 proteins occurs are the leptotene and zygotene stages, suggesting that meiotic recombination begins at the leptotene stage with the cooperation of these proteins and continues into zygotene.[5]
These proteins catalyze pairing of homologous chromosomes, DNA strand exchange, and recombinational repair of DNA damages.[7]
Major landmarks in human cytogenetics
[edit | edit source]- W.Waldeyer (1888) - Named chromosomes
- T.Boveri (1914) - Chromosome change could cause cancer
- Painter (1922) - Humans have 48 chromosomes
- Blakeslee and Avery (1937) - Colchicine as metaphase arrester
- T.C. Hsu (1952) - Hypotonic saline solution
- Tijo and Levan (1956) - Humans have 46 chromosomes
- J. Lejeune (1959)-Extra chromosome in Down Syndrome
- P. Nowell (1960) - Phytohemagglutinin (PHA) for lymphocyte culture
- Moorehead et al (1960) - Blood culture
- Caspersson et al (1968) - Q band
- Gall and Pardue (1969) - insitu hybridisation using radioactive probes
- Sumner et al (1971) - G banding
- Dutrillaux and Lejeune (1971) - R band
- P. Perry and S. Wolff (1974) - Sister Chromatid Exchange staining
- Goodpasture and Bloom (1975) - NOR silver staining
- Yunis et al (1979) - High resolution G banding
- P. R. Langer et al (1981) - Biotin Labeled probes in insitu hybridisation
- Spurbeck et al (1987) - Robotic Harvesting
- Ludecke (1989) - Microdissection of chromosomes
- Kallioniemi et al. (1991) - comparative genomic hybridisation (CGH)
- E. Schrock, Thomas Ried (1996) SKY technique
- M. Speicher (1996) - Multi color Fluorescence In Sity Hybridisation (M FISH)
- Chudoba I et al (1999) - Multicolor banding
- Nietzel A (2001) - centromere specific M FISH.
History of Classical Cytogenetics
[edit | edit source]- Walther Flemming published the first illustration of human chromosomes in 1882 and first used the term mitosis (Flemming, 1882). In 1888, Waldeyer introduced the term Chromosome, the Greek words for "colored body" (Waldeyer, 1888) soon after "chromosome theory of inheritance" came to an existence (Sutton, 1903; Boveri, 1902). Sutton combined two disciplines, cytology and genetics when he referred to the study of chromosome as cytogenetics. The ordered arrangement of chromosomes was termed as karyotype by Levitsky (Levitsky, 1924). A significant discovery in the field of cytogenetics was the use of "hypotonic shock" by Hsu and Pomerat to prepare a metaphase spread (Hsu and Pomerat, 1955). Later in the year, Ford and Hamerton used colchicine to accumulate dividing cells in metaphase (Ford and Hmerton, 1956). With all this technical advancement, Tijo and Levan found the human diploid chromosome number as 46 (Tijo and Levan, 1956) which was confirmed by subsequent studies. The technical advancements had continued with the use of mitogen by Nowell to stimulate peripheral blood lympocyte to divide (Nowell, 1960). Yet with this technical advancements the chromosomal rearrangments were not distinguishable until Caspersson's observation of plant chromosome stained with fluorescent quinacrine compunds where the chromosomes gave bright and dull patterns (Caspersson et al., 1968). In 1971, Caspersson and co-workers produced and reported a unique banding pattern for each human chromosome pair (Caspersson et al, 1971). The difficulties faced with the use of quinacrine were overcome when Drets and Shaw proposed a new method to produce similar banding pattern using an alkaline and saline pretreatment followed by staining with Giemsa (Drets and Shaw, 1971). With the ability to distinguish the human chromosomes with the specific banding pattern, the chromosomal rearrangments like chromosomal translocations, chromosomal inversions (including paracentric inversions), deletions, duplications, aneuploidies, microdeletions, insertions and mosaicisms had become identifiable.
History of Molecular Cytogenetics
[edit | edit source]- The first demonstration of in situ hybridization was carried out by Pardue and Gall in 1969 (Pardue and Gall 1969) using radiolabelled DNA on cytological preparation. Just after the success of their experiment they localized mouse satellite DNA onto mouse metaphase spreads (Pardue and Gall 1970). Over a decade later unique sequences were localized using cloned DNA (Harper and Saunders 1981; Harper et al 1981; Malcolm et al 1981). Due to the hazardous, complicated and slow experimental procedure the use of non-isotope labelling of DNA was sought (Bauman 1980; Bauman et al 1981). The most important development for the non isotope labelling of DNA was development of new method of conjugation of biotin to nucleotides (Langer et al 1981). Later on, biotin was incorporated in DNA or RNA enzymatically(Brigati et al 1983). The biotin labelled probes were detected using immunoflourescence (Albertson 1983) and by the use of fluoresceine isothiocyanate (FITC) conjugated avidin (Pinkel et al 1986) and the FISH technology emerged. Using fluorescence microscopes the hybridization can be visualized. With the use of recombinant nucleic acid technology and the ability to clone and amplify DNA segments in micro organisms has provided the richest source of probes for FISH. The types of probes used are mainly influenced by the nature of the target sequences and by the complexity of the cloned insert. For repeat sequence targest such as alphoid and satellite DNA, plasmid vectors are most commonly used while for the region specific or locus specific targets ranging from 1kb to just over 1 Mb Bacterial Artificial Chromosomes (BACs), P1 derived Artificial chromosomes (PACs), Yeast Artificial Chromosomes (YACs) or Cosmids are commonly used. Another breakthrough was a development of chromosome painting using flow sorted chromosome libraries (Cremer et al 1988a,b; Lichter et al 1988a,b; Pinkel et al 1988). Apart from flow sorting the whole chromosome painting probes (WCPs) can also be generated using chromosome microdissection (Guan et al 1994). In a sgnificant development, Nederlof presented simultaneous detection of more than three target sequences using FISH (Nederlof et al., 1990). Using this principle, the separation of all 24 different human chromosomes via multiplex fluorescence in situ hybridization (M-FISH) (Speicher et al., 1996, Eils et al., 1998), spectral karyotyping (SKY) (Schröck et al., 1996), Combined Binary RAtio labeling-FISH (COBRA FISH) (Tanke et al. 1999), color-changing karyotyping (CCK) (Henegariu et al. 1999) and IPM-FISH (Aurich-costa et al., 2001) has been established. However, these methods cannot detect pericentric and paracentric inversions and precisely identify chromosome breakpoints. To overcome the limitations of previously developed FISH techniques, a new high resolution multicolor banding (MCB) method was developed (Chudoba I et al., 1999) and tested on the example of chromosome 5. The major advantage of this technique is the MCB pattern, which can be aligned with the GTG banding (Lemke et al., 2001), is independent of the length of the analyzed chromosomes (Chudoba I et al, 1999) and a resolution higher than of GTG banding can be achieved. The advantages of the MCB technique was made available to all human chromosomes by developing 24 MCB probe sets, a specific one for each human chromosome( Liehr et al. 2001). As pointed out by Weise et al. (2003), MCB can be efficiently used for roughly mapping breakpoints or narrowing critical regions, but precise localization of breakpoints required subsequent BAC mapping. Later, MCB approach was used by Schmidt et al (2005) to narrow down the breakpoints of pericentric inversions.Weise et al. (2008) introduced Parental-origin-determination fluorescence in situ hybridization for distinguishing homologous human chromosomes on a single-cell level.
See also
[edit | edit source]References
[edit | edit source]- ↑ Rieger, R.; Michaelis, A.; Green, M.M. (1968), A glossary of genetics and cytogenetics: Classical and molecular, New York: Springer-Verlag, ISBN 9780387076683
- ↑ SemperBlotto (19 April 2008). "cytogenetics". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 28 March 2019.
{{cite web}}:|author=has generic name (help) - ↑ Kearney, Lyndal; Horsley, Sharon W. (September 2005). "Molecular cytogenetics in haematological malignancy: current technology and future prospects". Chromosoma 114 (4): 286–294. doi:10.1007/s00412-005-0002-z. ISSN 0009-5915. PMID 16003502.
- ↑ Bigner, S. H.; Schröck, E. (November 1997). "Molecular cytogenetics of brain tumors". Journal of Neuropathology and Experimental Neurology 56 (11): 1173–1181. ISSN 0022-3069. PMID 9370227.
- ↑ 5.0 5.1 Terasawa M, Shinohara A, Hotta Y, Ogawa H, Ogawa T. Localization of RecA-like recombination proteins on chromosomes of the lily at various meiotic stages. Genes Dev. 1995 Apr 15;9(8):925-34. PMID 7774810
- ↑ Anderson LK, Offenberg HH, Verkuijlen WM, Heyting C. RecA-like proteins are components of early meiotic nodules in lily. Proc Natl Acad Sci U S A. 1997 Jun 24;94(13):6868-73. PMID 11038554
- ↑ Harris Bernstein, Carol Bernstein and Richard E. Michod (2011). Meiosis as an Evolutionary Adaptation for DNA Repair. Chapter 19 pages 357-382 in "DNA Repair" (Inna Kruman editor). InTech Open Publisher. doi:10.5772/25117 ISBN 978-953-307-697-3 http://www.intechopen.com/books/dna-repair/meiosis-as-an-evolutionary-adaptation-for-dna-repair
External links
[edit | edit source]- Association for clinical cytogeneticists
- European cytogeneticists association (ECA)
- GenomeNet KEGG database
- Home - Gene - NCBI
- Atlas of Genetics and Cytogenetics in Oncology and Hematology
- Chromosomal variation in man
- Mitelman Database of Chromosome Aberrations in Cancer
- Online Mendelian Inheritance in Man
- FISH guide and troubleshooting
- List of articles on multicolor FISH
- Resources for molecular cytogenetics
- Cytogenetic Resources
- BLAST human sequences
- Ensembl project
- Map viewer
- Repeat masker
- UCSC Genome browser
- Online open access journal
