Geochronology/Radiocarbon dating

This is a natural reserve of peat at Frasne, France. Credit: Jeffdelonge.{{free media}}

Radiocarbon dating is a geochronology and archaeology technique that benefits from radiocarbon capture from the atmosphere and spallation creation of radiocarbon below the atmosphere especially and perhaps in the atmosphere as well.

Neutron astronomy

Main resource: Radiation/Neutrons

This image shows a Bonner Ball Neutron Detector which is housed inside the small plastic ball when the top is put back on. Credit: NASA.

Around EeV (10¹⁸ eV) energies there may be associated ultra high energy neutrons “observed in anisotropic clustering ... because of the relativistic neutrons boosted lifetime.” “[A]t E_n = 10²⁰ eV, [these neutrons] are flying a Mpc, with their directional arrival (or late decayed proton arrival) ... more on-line toward the source.” Although “neutron (and anti-neutron) life-lengths (while being marginal or meaningless at tens of Mpcs, the growth of their half-lives with energy may naturally explain an associated, showering neutrino halo.”

The Bonner Ball Neutron Detector "BBND ... determined that galactic cosmic rays were the major cause of secondary neutrons measured inside ISS. The neutron energy spectrum was measured from March 23, 2001 through November 14, 2001 in the U.S. Laboratory Module of the ISS. The time frame enabled neutron measurements to be made during a time of increased solar activity (solar maximum) as well as observe the results of a solar flare on November 4, 2001."

"BBND results show the overall neutron environment at the ISS orbital altitude is influenced by highly energetic galactic cosmic rays, except in the South Atlantic Anomaly (SAA) region where protons trapped in the Earth's magnetic field cause a more severe neutron environment. However, the number of particles measured per second per square cm per MeV obtained by BBND is consistently lower than that of the precursor investigations. The average dose-equivalent rate observed through the investigation was 3.9 micro Sv/hour or about 10 times the rate of radiological exposure to the average US citizen. In general, radiation damage to the human body is indicated by the amount of energy deposited in living tissue, modified by the type of radiation causing the damage; this is measured in units of Sieverts (Sv). The background radiation dose received by an average person in the United States is approximately 3.5 milliSv/year. Conversely, an exposure of 1 Sv can result in radiation poisoning and a dose of five Sv will result in death in 50 percent of exposed individuals. The average dose-equivalent rate observed through the BBND investigation is 3.9 micro Sv/hour, or about ten times the average US surface rate. The highest rate, 96 microSv/hour was observed in the SAA region."

Neutron colors

Main resource: Radiation astronomy/Colors

The neutron detection temperature, also called the neutron energy, indicates a free neutron's kinetic energy, usually given in electron volts. The term temperature is used, since hot, thermal and cold neutrons are moderated in a medium with a certain temperature. The neutron energy distribution is then adopted to the Maxwellian distribution known for thermal motion. Qualitatively, the higher the temperature, the higher the kinetic energy is of the free neutron. Kinetic energy, speed and wavelength of the neutron are related through the De Broglie relation.

Moderated and other, non-thermal neutron energy distributions or ranges are

• Fast neutrons: kinetic energies greater than 1 eV, 0.1 MeV or approximately 1 MeV, depending on the definition.
• Slow neutrons: a kinetic energy less than or equal to 0.4 eV.
• Epithermal neutrons: an energy from 1 eV to 10 keV.
• Hot neutrons: an energy of about 0.2 eV.
• Thermal neutrons: an energy of about 0.025 eV. This is the most probable energy, while the average energy is 0.038 eV.
• Cold neutrons: an energy from 5 × 10⁻⁵ eV to 0.025 eV.
• Very cold neutrons: an energy from 3 × 10⁻⁷ eV to 5 × 10⁻⁵ eV.
• Ultra cold neutrons: an energy less than 3 × 10⁻⁷ eV.
• Continuum region neutrons: an energy from 0.01 MeV to 25 MeV.
• Resonance region neutrons: an energy from 1 eV to 0.01 MeV.
• Low energy region neutrons: an energy less than 1 eV.

Fast neutrons

The ¹⁴
C produced by fast neutrons in the reaction ¹⁶O(n,³He)¹⁴C in the stratosphere depends on oxygen composing 28 % of the atmosphere; i.e. 25-28 % more ¹⁴
C is likely to be produced because fast neutrons are much more plentiful in the stratosphere. This ¹⁴
C may be produced even before neutrons thermalize for the expected reaction.

"THE first suggestion that appreciable ¹⁴
C might be produced in situ in polar ice was made by Fireman and Norris¹, who studied ¹⁴
C in CO₂ extracted from both accumulation and ablation samples. In some ablation samples they observed ¹⁴
C activities between four and six times higher than those expected due to trapped atmospheric CO₂."

"The ¹⁴C is produced mainly by nuclear spallations of oxygen in ice. The observed concentration of ¹⁴C in ablation ice samples is 1–3 x 10³ atom per g ice, three orders of magnitude higher than expected from the amount of trapped atmospheric CO₂ in this ice."

"The in situ ¹⁴C has a unique signature: about 60% exists as ¹⁴CO and the remainder as ¹⁴CO₂."

"Significant in situ production of radiocarbon by fast neutrons is restricted to the first ~15 m of firn, while the pore closure at this site occurs at 71 m depth [7]. So it is to be expected that most of the in situ produced ¹⁴
CO
₂ and ¹⁴
CO will diffuse out of the firn matrix and subsequently escape via the pores before these are closed, although a small fraction may stay behind."

"The ¹⁴
C activities of the CO fractions are close to the background value for CO blanks. A mean concentration of 9 ± 6 molecules ¹⁴
CO/g ice was deduced for the three ice samples. The relatively large error is primarily caused by the observed fluctuations in the background level. When this result is combined with the in situ ¹⁴
CO
₂/¹⁴
CO ratio of 3.8 [4], this leads to approximately 40 in situ produced ¹⁴
C atoms per gram of ice. For ice still containing all in situ produced ¹⁴
C atoms (no escape before pore closure), the ¹⁴
C concentration can be calculated using the model by Lal et al. [1]. For the altitude, latitude and meteorological data [7,9] of the present location we find approximately 2400 at./g. So we observe that ~98% of the in situ produced ¹⁴
C escaped from the firn before pore closure. This result compares well with the ~3% retained in situ ¹⁴
C, obtained by Wilson and Donahue [5] on two ice samples of the GISP ice core."

Disregarding "in situ production of radiocarbon would make the correlation worse: the radiocarbon ages would become younger. The large uncertainty in radiocarbon AD age for the youngest samples is mainly caused by the radio- carbon calibration curve."

"To compare our radiocarbon ages with ages derived from volcanic horizon identification with di-electrical profiling (DEP)/electrical DC conductivity (ECM) measurements, the age difference between trapped air and the ice matrix must be known. The age of the ice matrix at pore closure, at this site, can be calculated from the accumulation rate (62 mm water equivalent/yr), the -10 m temperature (-38.5°C) and the initial density of the snow pack (325 kg/m³) [7,9,11], which leads to 740 yr. According to Schwander and Stauffer [12], the average age difference between the air captured in the ice and the ice matrix is equal to the age of the ice matrix at a density of 815 kg/m³. For this site [Dronning Maud Land, Antarctica], this leads to 670 yr (estimated error ± 100 yr), [...]. (At 815 kg/m³ ca. 50% of the air which will be eventually in the ice has been trapped.)"

The "results obtained at this site by radiocarbon dating of ice at shallow depth cannot compete in accuracy with those obtained by the DEP/ECM methods. However, for drill sites with very low accumulation rates, sites where hiati exist, or at greater depth where stratigraphical methods become more uncertain due to layer thinning, ¹⁴
C measurements can provide absolute age estimates of the captured air from which ages of the ice matrix can be approximated."

"The Earth's magnetic field deflects incoming charged particles so that the equatorial cosmic-ray flux is four times less than the polar flux [...]."

"Spallation of atmospheric oxygen nuclei might contribute up to 20% to production of ¹⁴
C produced in the atmosphere (Lal and Peters 1967)."

"The fraction of cosmogenic ¹⁴
C produced below the atmosphere at the earth’s surface is estimated to be less than 0.1% of the total (Lal 1988a, 1992b)."

Slow neutrons

"The sharp dependence on energy of the cadmium cross section for neutrons of energies near 0.35 eV [slow neutrons] has been used to investigate the energy distribution of 0.35-ev neutrons scattered through 90° by lead, aluminum, diamond, and graphite."

Thermal neutrons

A thermal neutron is a free neutron with a kinetic energy of about 0.025 eV (about 4.0×10⁻²¹ J or 2.4 MJ/kg, hence a speed of 2.2 km/s), which is the most probable energy at a temperature of 290 K (17 °C or 62 °F), the mode of the Maxwell–Boltzmann distribution for this temperature.

After a number of collisions with nuclei (scattering) in a medium (neutron moderator) at this temperature, neutrons arrive at about this energy level, provided that they are not absorbed.

Thermal neutrons have a different and sometimes much larger effective neutron absorption cross-section for a given nuclide than fast neutrons, and can therefore often be absorbed more easily by an atomic nucleus, creating a heavier, often unstable isotope of the chemical element as a result (neutron activation).

Neutron sources

Main resource: Radiation astronomy/Sources

Neutron emitters to left of lower dashed line

Z →	0	1	2
n ↓	n	H	He	3	4
0		1H		Li	Be	5	6
1	1n	2H	3He	4Li	5Be	B	C	7
2	2n	3H	4He	5Li	6Be	7B	8C	N	8
3		4H	5He	6Li	7Be	8B	9C	10N	O	9
4	4n	5H	6He	7Li	8Be	9B	10C	11N	12O	F	10
5		6H	7He	8Li	9Be	10B	11C	12N	13O	14F	Ne	11
6		7H	8He	9Li	10Be	11B	12C	13N	14O	15F	16Ne	Na	12
		7	9He	10Li	11Be	12B	13C	14N	15O	16F	17Ne	18Na	Mg	13
		8	10He	11Li	12Be	13B	14C	15N	16O	17F	18Ne	19Na	20Mg	Al	14
			9	12Li	13Be	14B	15C	16N	17O	18F	19Ne	20Na	21Mg	22Al	Si
				10	14Be	15B	16C	17N	18O	19F	20Ne	21Na	22Mg	23Al	24Si
					11	16B	17C	18N	19O	20F	21Ne	22Na	23Mg	24Al	25Si
						12	18C	19N	20O	21F	22Ne	23Na	24Mg	25Al	26Si
							13	20N	21O	22F	23Ne	24Na	25Mg	26Al	27Si
								14	22O	23F	24Ne	25Na	26Mg	27Al	28Si

Neutrons are produced when alpha particles impinge upon any of several low atomic weight isotopes including isotopes of lithium, beryllium, carbon and oxygen.

Gamma radiation with an energy exceeding the neutron binding energy of a nucleus can eject a neutron. Two examples and their decay products:

⁹Be + >1.7 Mev photon → 1 neutron + 2 ⁴He

²H (deuterium) + >2.26 MeV photon → 1 neutron + ¹H

Traditional particle accelerators with hydrogen (H), deuterium (D), or tritium (T) ion sources may be used to produce neutrons using targets of deuterium, tritium, lithium, beryllium, and other low-Z materials. Typically these accelerators operate with voltages in the > 1 MeV range.

Neutrons (so-called photoneutrons) are produced when photons above the nuclear binding energy of a substance are incident on that substance, causing it to undergo giant dipole resonance after which it either emits a neutron (photodisintegration) or undergoes fission (photofission). The number of neutrons released by each fission event is dependent on the substance. Typically photons begin to produce neutrons on interaction with normal matter at energies of about 7 to 40 MeV, which means that megavoltage photon radiotherapy facilities may produce neutron radiation as well, and require special shielding for it. In addition, electrons of energy over about 50 MeV may induce giant dipole resonance in nuclides by a mechanism which is the inverse of internal conversion, and thus produce neutrons by a mechanism similar to that of photoneutrons.

A spallation source is a high-flux source in which protons that have been accelerated to high energies hit a target material, prompting the emission of neutrons.

Nuclear fusion, the combining of the heavy isotopes of hydrogen, also has the potential to produce large quantities of neutrons.

Neutron emission is a type of radioactive decay of atoms containing excess neutrons, in which a neutron is simply ejected from the nucleus. Two examples of isotopes which emit neutrons are beryllium-13 (mean life 2.7x10^-21 sec) and helium-5 (7x10^-22 sec).

Neutron emission usually happens from nuclei that are in an excited state, such as the excited O-17* produced from the beta decay of N-17. The neutron emission process itself is controlled by the nuclear force and therefore is extremely fast, sometimes referred to as "nearly instantaneous." The ejection of the neutron may be as a product of the movement of many nucleons, but it is ultimately mediated by the repulsive action of the nuclear force that exists at extremely short-range distances between nucleons. The life time of an ejected neutron inside the nucleus before it is emitted is usually comparable to the flight time of a typical neutron before it leaves the small nuclear "potential well," or about 10^-23 seconds. A synonym for such neutron emission is "prompt neutron" production, of the type that is best known to occur simultaneously with induced nuclear fission. Many heavy isotopes, most notably californium-252, also emit prompt neutrons among the products of a similar spontaneous radioactive decay process, spontaneous fission.

Most neutron emission outside prompt neutron production associated with fission (either induced or spontaneous), is from neutron-heavy isotopes produced as fission products. These neutrons are sometimes emitted with a delay, giving them the term delayed neutrons, but the actual delay in their production is a delay waiting for the beta decay of fission products to produce the excited-state nuclear precursors that immediately undergo prompt neutron emission. Thus, the delay in neutron emission is not from the neutron-production process, but rather its precursor beta decay which is controlled by the weak force, and thus requires a far longer time. The beta decay half lives for the precursors to delayed neutron-emitter radioisotopes, are typically fractions of a second to tens of seconds.

Cosmic rays

Main resource: Radiation/Cosmic rays

The flux of cosmic-ray particles is a function of their energy. Credit: Sven Lafebre, after Swordy.

Cosmic rays cause spallation when a ray particle (e.g. a proton) impacts with matter, including other cosmic rays. The result of the collision is the expulsion of large numbers of nucleons (protons and neutrons) from the object hit.

At right is an image indicating the range of cosmic-ray energies. The flux for the lowest energies (yellow zone) is mainly attributed to solar cosmic rays, intermediate energies (blue) to galactic cosmic rays, and highest energies (purple) to extragalactic cosmic rays.

Here's a quote from Bowman's "Radiocarbon Dating" book from 1990, p. 19: "High sunspot activity increases the weak magnetic field that exists between the planets, and at such times there is a greater deflection of cosmic rays and hence ¹⁴C decreases."

"Cosmic rays originate from the Sun as well as from galactic sources."

Here's a quote from Aitken's "Radiocarbon Dating" article from 2000, "Cosmic-ray variations are associated with changes in the strength of the Earth's magnetic field. A weak field allows more cosmic radiation to reach the upper atmosphere, and the production of carbon-14 is consequently enhanced--causing raw radiocarbon ages to be underestimates of calendar ages. The short-term wiggles mentioned above are associated with sunspot activity."

"Direct observations of cosmic rays within the heliosphere over several decades have revealed a great deal of information about the acceleration and propagation of cosmic radiation through the interstellar space and the heliosphere. We now know that the cosmic radiation incident at the top of the earth’s atmosphere comes to us through several “filters”:

1. Galactic magnetic fields,
2. Interstellar magnetic fields,
3. Solar magnetic plasma within the heliosphere, regulated by solar activity, and finally,
4. the Terrestrial geomagnetic field."

"Additionally, cosmic ray particles are frequently accelerated by the sun, and sometimes in a nearby supernova to make an appreciable difference in the total cosmic ray flux at the earth!"

"Since fairly extensive cosmic-ray data on primary and secondary cosmic rays are available for more than the past five decades, covering five solar cycles, it is fairly easy to make reliable calculations of the magnitude of variations in cosmogenic production rates in terrestrial solids due to solar modulation of galactic cosmic-ray flux. This exercise is based on a study of relative changes in the primary cosmic-ray flux at the top of the atmosphere, and flux of low energy neutrons as measured by neutron monitors. Solar modulation of galactic cosmic-ray flux is conveniently described in terms of a modulation potential, ∅, which is a phase-lagged function of solar activity (see Castagnoli and Lal 1980; Lal 1988b, 2000 and references therein). Continuous data are available for several neutron monitors at sea-level and mountain altitudes located at different latitudes, and these data have been analyzed in terms of transfer functions relating changes in the secondary nucleon fluxes in the atmosphere to those in the primary cosmic-ray spectra (cf. Webber and Lockwood 1988; Nagashima et al. 1989). For a recent discussion on changes in cosmic-ray fluxes as measured on spacecrafts and in neutron monitor counting rates, the reader is referred to Lal (2000). The manner in which the primary and secondary cosmic-ray flux changes occur with the march of solar activity is described in detail by Lal and Peters (1967), who also estimate the changes in the isotope production rates as a function of altitude and latitude during 1956 (a period of solar minimum) and 1958 (a period of unusually high solar activity). Using this approach, and using the neutron monitor data available to date, one can improve on the earlier estimates of solar temporal variations in cosmogenic nuclide production rates at sea level and at mountain altitudes. We must mention here that several direct experiments are also being made at present by exposing targets to cosmic radiation at different altitudes and latitudes (cf. Lal 2000)."

Solar cosmic rays

This image shows an overview of the space weather conditions over several solar cycles including the relationship between sunspot numbers and cosmic rays. Credit: Daniel Wilkinson.

File:Solar magnetic flux.png

Comparison shows the observed (solar irradiance and sunspot number, symbols) and modeled (solid line) total magnetic flux Credit: Luis Eduardo A. Vieira and Sami K. Solanki.{{fairuse}}

"A persistent problem of solar cosmic-ray research has been the lack of observations bearing on the timing and conditions in which protons that escape to the interplanetary medium are first accelerated in the corona."

For solar cosmic-rays, the apparent lack of proton acceleration in the corona seems justified, in contrast to the electrons, proton bremsstrahlung and gyrosynchrotron emission are negligible. This suggests a transit time anomaly, ΔT_A, defined as follows:

ΔT_A = ΔT_onset - 11 min,

where ΔT_onset is the deduced Sun-Earth transit time for the first arriving relativistic protons and 11 min is the nominal transit time for a ~2 GeV proton traversing a 1.3 AU Archimedes spiral path." "The solar wind is a stream of charged particles ejected from the upper atmosphere of the Sun. It mostly consists of electrons and protons with energies usually between 1.5 and 10 keV.

ΔT_A may have values from "7-19 min for a small sample of well-connected ... cosmic-ray flares." The transit time anomaly may be explained by a rise time associated with the ground-level events (GLEs). "The average GLE rise time ... for well-connected ... events ... defined to be the time from event onset to maximum as measured by the neutron monitor station showing the largest increase and whose asymptotic cone of acceptance ... includes the nominal direction of the Archimedean spiral path, is 21.3 min."

"Data from an extensive air shower detector of ultrahigh-energy cosmic rays shows shadowing of the cosmic-ray flux by the Moon and the Sun with significance of 4.9 standard deviations. This is the first observation of such shadowing."

"The ... solar proton flare on 20 April 1998 at W 90° and S 43° (9:38 UT) was measured by the GOES-9-satellite (Solar Geophysical Data 1998), as well as by other experiments on WIND ... and GEOTAIL. Protons were accelerated up to energies > 110 MeV and are therefore able to hit the surface of Mercury."

Solar winds

"Energetic photons, ions and electrons from the solar wind, together with galactic and extragalactic cosmic rays, constantly bombard surfaces of planets, planetary satellites, dust particles, comets and asteroids."

The solar wind is divided into two components, respectively termed the slow solar wind and the fast solar wind. The slow solar wind has a velocity of about 400 km/s, a temperature of 1.4–1.6×10⁶ K and a composition that is a close match to the corona. By contrast, the fast solar wind has a typical velocity of 750 km/s, a temperature of 8×10⁵ K and it nearly matches the composition of the Sun's photosphere. The slow solar wind is twice as dense and more variable in intensity than the fast solar wind. The slow wind also has a more complex structure, with turbulent regions and large-scale structures.

The slow solar wind appears to originate from a region around the Sun's equatorial belt that is known as the "streamer belt". Coronal streamers extend outward from this region, carrying plasma from the interior along closed magnetic loops. Observations of the Sun between 1996 and 2001 showed that emission of the slow solar wind occurred between latitudes of 30–35° around the equator during the solar minimum (the period of lowest solar activity), then expanded toward the poles as the minimum waned. By the time of the solar maximum, the poles were also emitting a slow solar wind.

The fast solar wind is thought to originate from coronal holes, which are funnel-like regions of open field lines in the Sun's magnetic field. Such open lines are particularly prevalent around the Sun's magnetic poles. The plasma source is small magnetic fields created by convection cells in the solar atmosphere. These fields confine the plasma and transport it into the narrow necks of the coronal funnels, which are located only 20,000 kilometers above the photosphere. The plasma is released into the funnel when these magnetic field lines reconnect.

Galactic cosmic rays

File:NeutronMonitor.GIF

Cosmic Ray Intensity (blue) and Sunspot Number (green) is shown from 1951 to 2006 Credit: University of New Hampshire.{{fairuse}}

The graph on the right shows an inverse correlation between sunspot numbers (solar activity) and neutron production from galactic cosmic rays.

Cosmic-ray astronomy

Main resource: Radiation/Cosmic rays

"Cosmic rays arise from galactic source accelerators."

Cosmic rays may be upwards of a ZeV (10²¹ eV).

About 89% of cosmic rays are simple protons or hydrogen nuclei, 10% are helium nuclei of alpha particles, and 1% are the nuclei of heavier elements. Solitary electrons constitute much of the remaining 1%.

Def. cosmic rays that originate from astrophysical sources are called primary cosmic rays.

Def. cosmic rays that are created when primary cosmic rays interact with interstellar matter are called secondary cosmic rays.

Def. low energy cosmic rays associated with solar flares are called solar cosmic rays.

Cosmic rays are not charge balanced; that is, positive ions heavily outnumber electrons. The positive ions are

1. free protons,
2. alpha particles (helium nuclei),
3. lithium nuclei,
4. beryllium nuclei, and
5. boron nuclei.

Def. a nuclear reaction in which a nucleus fragments into many nucleons is called spallation.

Cosmic rays cause spallation when a ray particle (e.g. a proton) impacts with matter, including other cosmic rays. The result of the collision is the expulsion of large numbers of nucleons (protons and neutrons) from the object hit.

Carbon and oxygen nuclei collide with interstellar matter to form lithium, beryllium and boron in a process termed cosmic ray spallation. Spallation is also responsible for the abundances of scandium, titanium, vanadium, and manganese ions in cosmic rays produced by collisions of iron and nickel nuclei with interstellar matter.

Carbons

Carbon-14 is produced in the upper layers of the troposphere and the stratosphere by thermal neutrons absorbed by nitrogen atoms. When cosmic rays enter the atmosphere, they undergo various transformations, including the production of neutrons. The resulting neutrons (¹n) participate in the following reaction:

n + ¹⁴
₇N
→ ¹⁴
₆C
+ p

The highest rate of carbon-14 production takes place at altitudes of 9 to 15 km (30,000 to 49,000 ft) and at high geomagnetic latitudes.

"¹⁴
C is produced in the upper atmosphere by the bombardment of ¹⁴
N by thermal neutrons [...], mainly initiated by high energy galactic cosmic rays, although less energetic solar cosmic rays also contribute to the production of ¹⁴
C (Libby, 1946). These primary cosmic rays lose energy through ionization of molecules and interactions with atomic nuclei as they travel through the Earth’s atmosphere, forming secondary particles: mainly neutrons, protons and muons (Tuniz et al., 1998; Muziker et al., 2003). A proportion of secondary particles, known as fast neutrons, lose further energy through nuclear collisions to form thermal neutrons, which are in vibrational equilibrium with atmospheric gases (Gosse and Phillips, 2001)."

"Rapid circulation of atmospheric ¹⁴
CO
₂, on the order of 4-10 years (Craig, 1957a; Nydal and Lövseth, 1970), ensures an almost uniform global atmospheric ¹⁴
C concentration at any point in time, although certain factors can influence the rate of production of ¹⁴
C (and consequently ¹⁴
CO
₂) over time, including latitude, altitude and solar activity. Understanding these variations in ¹⁴
C concentration is fundamental to the calculation of accurate ¹⁴
C ages, and their subsequent interpretation."

"Magnetic fields induced by solar activity also affect ¹⁴
C production, as high solar activity increases the flux of solar magnetic particles that deflect cosmic rays away from the Earth, thus decreasing ¹⁴
C production rates in the Earth’s atmosphere (Stuiver et al., 1997). Changes in solar activity therefore correlate with ¹⁴
C activity, and the periodicity is evident throughout the solar cycles that affect irradiance on the Earth. Therefore, regular variations in the flux of high energy galactic cosmic rays are evident in the ¹⁴
C record. 11 year Schwabe variations involve one cycle of increasing/decreasing sunspot activity and one reversal of the solar magnetic field, with ¹⁴
C production reaching a maximum of 1.15 times the normal production rate during periods of minimum solar activity (Masarik and Beer, 1999). 210 year Suess cycles (Masuda et al., 2009) and 2300 year Hallstatt cycles (Tobias et al., 2004; Clilverd et al., 2003, 2004) have similar effects, modulating ¹⁴
C production in inverse proportion to solar activity."

"One such [atmospheric] variation is the 56 ± 24 ¹⁴
C yr offset noted between the Northern and Southern Hemispheres (McCormac et al., 2004). This offset remains broadly constant, although some temporal variations do occur. Known as the North/South Hemisphere effect, it occurs because the Southern Hemisphere contains an area of ocean c 40% greater than that of the Northern (Aitken, 1990, Levin et al., 1987). This results in the Southern Hemisphere having a greater area of ocean / air interface available for exchange between atmospheric CO
₂ and oceanic bicarbonate. Oceanic bicarbonate is depleted in ¹⁴
C relative to atmospheric CO
₂ because of the extended residence time of ¹⁴
C in the marine environment known as the marine reservoir effect (MRE). [...] This is accounted for during the calibration process with separate calibration curves (IntCal09 for the Northern Hemisphere (Reimer et al., 2009), SHCal04 for the Southern Hemisphere (McCormac et al., 2004))."

"Separate calibration curves have been constructed for the atmospheric (terrestrial) environment (INTCAL09 (Reimer et al., 2009)) and the marine environment (MARINE 09 (Reimer et al., 2009) [MARINE 13 calibration dataset (Reimer et al., 2013)]) to account for the large offset in ¹⁴
C concentration between the two reservoirs caused by the MRE."

The rate of ¹⁴C production can be modelled and is between 16,400 and 18,800 atoms ¹⁴C m⁻²s⁻¹, which agrees with the global carbon budget that can be used to backtrack, but attempts to directly measure the production rate in situ were not very successful. Production rates vary because of changes to the cosmic ray flux caused by the heliospheric modulation (solar wind and solar magnetic field), and due to variations in the Earth's magnetic field. The latter can create significant variations in ¹⁴C production rates, although the changes of the carbon cycle can make these effects difficult to tease out. Occasional spikes may occur; for example, there is evidence for an unusually strong increase of the production rate in AD 774–775, caused by an extreme solar energetic particle event, strongest for the last ten millennia. Another "extraordinarily large" ¹⁴C increase (20‰) has been recently (2017) associated with the 5480 BC event, which is however unlikely to be a solar energetic particle event.

Carbon-14 may also be produced by lightning bolts but in the amounts negligible compared to cosmic rays.

	→ 8 C	→ 9 C	→ 10 C	→ 11 C	→ 12 C	→ 13 C	→ 14 C	→ 15 C	→ 16 C	→ 17 C	→ 18 C	→ 19 C	→ 20 C	→ 21 C	→ 22 C
(p,?)		10 N + p? → 9 C + p		11 B + p → 11 C + ?			13 C + n → 14 C + γ
(p,d)			11 N + p? → 10 C + p	12 C + p → 11 C + d			13 C + n → 14 C + γ
(p,α)				14 N + p → 11 C + α			13 C + n → 14 C + γ
(n,γ)							13 C + n → 14 C + γ
(n,p)				11 B			14 N + n → 14 C + p
(n,p)					12 B + p → 12 C		14 N + n → 14 C + p
(n,d)							15 N + n → 14 C + d
(n?,e+)					12 N + n? → 12 C + e+	13 N + n? → 13 C + e+
(n,d)							15 N + n → 14 C + d
(n,e-)					16 N + n? → 12 C + e-	17 N + n? → 13 C + e-	18 N + n? → 14 C + e-
(n,3 He)							16 O + n → 14 C + 3 He
(n,α)							17 O + n → 14 C + α
(d,?)				10 B + d → 11 C + ?			17 O + n → 14 C + α

Carbon-14 can also be produced by ¹⁶O(n,³He)¹⁴C with fast neutrons.

The ¹⁴
C produced by fast neutrons in the reaction ¹⁶O(n,³He)¹⁴C in the stratosphere depends on oxygen composing 28 % of the atmosphere; i.e. 25-28 % more ¹⁴
C is likely to be produced because fast neutrons are much more plentiful in the stratosphere. This ¹⁴
C may be produced even before neutrons thermalize for the expected reaction.

Carbon-14 may also be radiogenic (cluster decay of ²²³Ra, ²²⁴Ra, ²²⁶Ra). However, this origin is extremely rare.

¹⁴C production routes

Parent isotope	Natural abundance, %	Cross section for thermal neutron capture, barns	Reaction
13 C	1.103	0.0009	13 C(n,γ)14 C
14 N	99.634	1.81	14 N(n,p)14 C
16 O	99.9627?	0.235?	16 O(n,3 He)14 C
17 O	0.0383	0.235	17 O(n,α)14 C

Radiocarbon half-life

In 1952, the "weighted mean of these three determinations, 5568 ± 30, is probably accurate to within 50 years and almost certainly within 100 years."

With ¹⁴C, Libby's team did not obtain the correct half-life the first time. So now a convention has been set up to convert older ages to correct ages. This convention uses 8267 and 8033 as absolute values into their respective equations.

But in 1949, "The half-life of C¹⁴ has been found to be 5720 ± 47 years by means of the use of mass spectrometrically analyzed C¹⁴O₂ as a part of the counter gas in brass wall Geiger counters."

In 1962, "A more accurate half-life has been measured as 5730 ± 40 years (Godwin, 1962)."

"The neutrons in the air being formed by the energetic cosmic rays possess energy themselves, probably of the order of 5-10 mev (million electron volts) on the average when first formed. After birth they then collide with air molecules and lose their energy by collision, either elastic or inelastic, either reacting on one of these collisions and so being absorbed or finally attaining thermal energies where they are quite certain to be absorbed to form radiocarbon by Reaction 1 [n + ¹⁴
₇N
→ ¹⁴
₆C
+ ¹
₁H
]. Laboratory studies of the effects of energetic neutrons on air again indicate that the nitrogen is the more reactive constituent."

"The determination of the half-life of carbon-14 has been a major problem. In 1949, Libby, in collaboration with A. G. Engelkemeir, W. H. Hamil, and M.G. Inghram (Engelkemeir et al., 1949; Engelkemeir and Libby, 1950) measured the half-life of carbon-14 and found it to be 5568 ± 45 years. At about that time independently obtained values of 5589 ± 75 (Jones, 1948) and 5513 ± 165 (Miller et al., 1950) also gave 5568 ± 30 when weighted according to the inverse square of the errors. Although these independently derived determinations seemed to confirm the 5568 year half-life and this value became the standard for measurement, a determination by W. B. Mann and W. F. Marlow of the National Bureau of Standards yielded a value of 5760 years (Finney, 1961). The present best estimate resulting from three additional determinations is 5730 ± 40 years (Godwin, 1962, p. 984)."

Two experimentally determined values from the early 1950s were not included in the value Libby used: ~6,090 years [Jenks and Sweeton, 1952], and 5900 ± 250 years [Caswell et al.].

Soil organic matter

"During the last decade radiocarbon dating has been used extensively in distinct regions of Brazil to provide information about soil chronology in paleoenvironmental studies. This paper presents ¹⁴C data of soil organic matter (SOM), humin fraction, and charcoal in several soil profiles under natural vegetation from different Brazil locations (north, central, and southeast regions). The main objective is to compare the obtained ¹⁴C dating of total SOM with humin, the oldest fraction of SOM. In order to validate the humin ages these data are compared with the age of charcoal collected at similar depths. The ¹⁴C ages obtained on charcoal were, in most of the cases, in agreement with the humin fraction considering the experimental errors, or 20% older in average. The dates obtained from total SOM showed significantly younger ages than the humin fraction indicating contamination by younger carbon. These results show the humin fraction is considered a reliable material for ¹⁴C dating in soils."

Humic acids

"The reliability of radiocarbon ages based on soil organic matter (SOM) from Holocene buried soils in Middle Park, Colorado, is assessed by comparison with ages of charcoal. On average, ¹⁴
C ages of SOM from buried surface horizons are 880 ± 230 ¹⁴
C yr younger than charcoal ages from the same horizon. Humic acid (HA) and low-temperature (400 °C) combustion residue (LT) fractions are 390 ± 230 and 1290 ± 230 ¹⁴
C yr younger than charcoal ages, respectively, and HA ages are on average 860 ± 140 ¹⁴
C yr older than LT fractions."

Humins

"Volcanic ash soils (Andosols) may offer great opportunities for paleoecological studies, as suggested by their characteristic accumulation of organic matter (OM). However, understanding of the chronostratigraphy of soil organic matter (SOM) is required. Therefore, radiocarbon dating of SOM is necessary, but unfortunately not straightforward. Dating of fractions of SOM obtained by alkali-acid extraction is promising, but which fraction (humic acid or humin) renders the most accurate ¹⁴
C dates is still subject to debate. To determine which fraction should be used for ¹⁴
C dating of Andosols and to evaluate if the chronostratigraphy of SOM is suitable for paleoecological research, we measured ¹⁴
C ages of both fractions and related calibrated ages to soil depth for Andosols in northern Ecuador. We compared the time frames covered by the Andosols with those of peat sequences nearby to provide independent evidence. Humic acid (HA) was significantly older than humin, except for the mineral soil samples just beneath a forest floor (organic horizons), where the opposite was true. In peat sections, ¹⁴
C ages of HA and humin were equally accurate. In the soils, calibrated ages increased significantly with increasing depth. Age inversions and homogenization were not observed at the applied sampling distances. [In] Andosols lacking a thick organic horizon, dating of HA renders the most accurate results, since humin was contaminated by roots. On the other hand, in mineral soil samples just beneath a forest floor, humin ages were more accurate because HA was then contaminated by younger HA illuviated from the organic horizons."

Peats

"In peats, a number of possible techniques for dating are available. Short-lived radioisotopes (²¹⁰
Pb, ²⁴¹
Am, ¹³⁷
Cs) are the most commonly used (Appleby et al. 1997), but this approach has shown variable results in some situations and often needs to be cross-checked with other chronological markers (Oldfield et al. 1995). Stable isotopes of lead have also been used successfully, especially to provide age markers in the 20th century (Martínez-Cortizas et al. 1999). Other useful age markers are spheroidal carbonaceous particles (SCPs; Yang et al. 2001), historical tephras (Schoning et al. 2005), and pollen markers (Barber et al. 1998). Used together, these techniques can provide a high-quality chronology for the last 100–150 yr. However, the quality of chronologies tends to decline for the early 20th and late 19th century, and dating is reliant on only a few markers before AD 1850. In addition, radiocarbon dating of single samples is of limited value for sediments from between AD 1650 and 1950 because of the plateau in the relationship between ¹⁴
C activity and calendar age over this period. One approach to extend peat chronologies back to around AD 1600, as well as to provide a cross-check on other techniques from AD 1850–1950, is to apply wiggle matching to a series of ¹⁴
C ages. This technique has been used with success in older peats (Kilian et al. 2000; Kilian et al. 1995; Mauquoy et al. 2002; Speranza et al. 2000), but has been attempted rather infrequently for more recent peats (Clymo et al. 1990; Gedye 1998)."

Lignites

"A particular source of potential contamination by old carbon occurs locally in the Babeldaob landscape in the form of soft lignite and dark gray organic clay within the kaolinitic Airai clay formation of upper Tertiary age, overlying the volcanic bedrock and saprolite. Indeed, kaolinitic Airai clay seen at three fairly extensive exposures (Nerassa, Oikull, Ulimang) was found to be flecked, commonly with black organic material, and to grade into dark gray organic clay overlying or underlying lignitic beds. The Airai clay is very suitable for pottery and is said to have been used in traditional Palauan manufacture near Oikull (Vince Blaiyok, personal communication). This is supported by Instrumental Neutron Activation Analysis (INAA) which identified Oikull and Ngimis as likely sources of clay used for making prehistoric pottery (Pavlish et al. 1986). [...] Considering that much of the clay is carbonaceous, it seems likely that ancient carbon could be retained in low-temperature pottery made from it."

"Old-carbon contamination of archaeological materials could occur also if they had been infused by groundwater which was carrying organic compounds derived from the lignite, or if a site was built up of materials that included the lignite. In contrast, mobilization of organic compounds derived from today’s soil could lead to young-carbon contamination. Contamination by both old and young carbon, either from lignitic sources or from soil charcoals of unknown age and derivation, could also occur, of course, through erosion and runoff into sedimentary basins."

"Since lignite deposits and dispersed fragments in saprolites could be mistaken for charcoal incorporated in pottery or deposited in sedimentary basins, there is a significant possibility of confusion in Palauan 14C dating."

Bituminous coals

"Bituminous coal, previously suspected as a contaminant in radiocarbon samples, has now been demonstrated to be a source of dating error in archaeological and geological samples. Standard laboratory procedures are inadequate to recognize or remove coal from samples, but techniques for identifying coal particles include paleo-botanical and reflectance analyses, and possibly accelerator dating."

Coals

"AMS-radiocarbon dating of specific organic fractions is used to evaluate sources of errors in dating of organic-poor lake sediment from Linnévatnet, a proglacial arctic lake. Dates on undifferentiated (bulk) organic matter are much too old because of contamination from detrital coal. Attempts to remove coal from other organic matter were only partially successful, a consequence of the wide grain-size distribution of the coal. Even if coal contamination is fully removed, the bulk of the remaining organic matter is of aquatic origin and is unsuitable for ¹⁴C dating because the lake waters are depleted in ¹⁴ C due to dissolution of carbonate minerals. Terrestrial plant macrofossils provide the only reliable material to date the lake sediment; however, this material is present in sufficient quantity for AMS-radiocarbon dating only in cores proximal to the main inlet streams. Paired dates on terrestrial plants and aquatic insects from the same core level and paired dates on modern aquatic and terrestrial vegetation indicate differences in carbon reservoir activities of 1000 and 3000 years. In hard-water lakes, coring is recommended in inlet-proximal areas where inwashed terrestrial vegetation is most concentrated. Chronologies established in proximal cores can be transferred to central-basin cores using litho or chemo-stratigraphic indices."

Charcoals

"Two fire-history parameters (time-since-fire [TSF] and fire extent) were related to three landscape parameters (landform [hill slope or terrace], aspect, and forest composition) at 83 sites in a 730-ha low-elevation (less than ∼200 m) area of a mountainous watershed. We dated fires using tree rings (18 sites) and 120 soil-charcoal radiocarbon dates (65 sites). Comparisons among multiple radiocarbon dates indicated a high probability that the charcoal dated at each site represented the most recent fire, though we expect greater error in TSF estimates at sites where charcoal was very old (>6000 yr) and was restricted to mineral soil horizons. TSF estimates ranged from 64 to ∼12 220 yr; 45% of the sites have burned in the last 1000 yr, whereas 20% of the sites have not burned for over 6000 yr. Differences in median TSF were more significant between landform types or across aspects than among forest types. Median TSF was significantly greater on terraces (4410 yr) than on hill slopes (740 yr). On hill slopes, all south-facing and southwest-facing sites have burned within the last 1000 yr compared to only 27% of north- and east-facing sites burning over the same period. Comparison of fire dates among neighboring sites indicated that fires rarely extended >250 m. During the late Holocene, landform controls have been strong, resulting in the bias of fires to south-facing hillslopes and thus allowing late-successional forest structure to persist for thousands of years in a large portion of the watershed. In contrast, the early Holocene regional climate and forest composition likely resulted in larger landscape fires that were not strongly controlled by landform factors."

"Radiocarbon age determinations of wood charcoal are commonly used to date past forest fire events, even though such ages should be greater than the fire event due to the age of the wood at the time of burning. The difference in the ¹⁴C-derived age of charcoal and the time-since-fire (the “inbuilt age”) may be considerable in some vegetation types and thus must be estimated before interpreting fire dates. Two methods were used to estimate the potential range of inbuilt age of soil charcoal dated to determine ages of forest fires on the west coast of Vancouver Island (Canada). First, 26 ¹⁴C ages on charcoal in surficial soil were compared directly with ages of forest fire determined by tree-ring counts, suggesting inbuilt ages of 0–670 years. Second, a simulation model that uses estimated fuel loads, fuel consumption, charcoal production, and the ages of charred wood (time since wood formation), suggests that the combination of slow growth rates and slow decay rates of certain species can account for inbuilt ages of more than 400 years in this forest type. This level of inbuilt age is large enough such that the actual age of a fire may not occur within the 2σ confidence interval of a calibrated charcoal ¹⁴C age determination, and thus significantly affect the interpretation of fire dates. A method is presented to combine the error of a calibrated ¹⁴C age determination with the error due to inbuilt age such that the larger adjusted error encompasses the actual age of the fire."

"Radiocarbon dating of early Pre-Pottery Neolithic B (PPNB) deposits at the site of Motza, Israel, was achieved by first prescreening many charcoal and bone samples in order to identify those that are in the most suitable state of preservation for dating. For assessing bone preservation, we determined the collagen contents, and by infrared spectroscopy the collagen purity. The collagen samples of the best preserved bones were then further characterized by their C/N ratios and amino acid compositions. Prescreening of the charcoal samples involved monitoring the changes in infrared and Raman spectra during the acid-alkali-acid treatments. In some samples, we noted that the clay content increased with additional alkali treatments. These samples were rejected, as this could result in erroneous dates. No differences were observed in the ¹⁴C dates between charcoal and bone collagen samples. The dates range from 10,600–10,100 cal BP, which is consistent with dates for the early PPNB from other sites."

"Subsamples of charcoal from a number of different excavation contexts at the early modern human (Homo sapiens) site of Niah Great Cave (Malaysia) were accelerator mass spectrometry (AMS) ¹⁴C dated. Samples were prepared using one of a number of different methods: untreated (control); acid–base–acid (ABA); and acid–base–wet oxidation with stepped combustion (ABOX-SC) after Bird et al. (1999). The results show that for material younger than ∼25 ka BP there is little difference between the two chemical pretreatment methods and the control. For charcoal beyond ∼25 ka BP, however, there are differences of up to 4000 a, with ABOX-SC ages being consistently older. This is argued to be a more effective pretreatment method for decontaminating charcoal samples prior to radiocarbon dating. For radiocarbon dating charcoals greater than ∼25 ka BP, the ABOX-SC pretreatment and combustion approach appears to be the most rigorous method for developing a robust chronological framework for tropical sequences and should be more widely applied in contexts where the material being dated is likely to be ancient. The new chronology developed for Niah Cave based on this technique suggests that the earliest human evidence dates back to at least 45 ka BP and may extend significantly earlier than this based on the recent discovery of lithics 50 cm below the earliest dated charcoal."

Graphites

"Graphite in various forms has become the standard target for accelerator ¹⁴C dating. Graphite has been made by catalytic graphitization of charcoals (Lowe, 1984). Thin films of graphite have also been produced by thermal cracking (Beukens & Lee, 1981), electric discharge (Andrée et al, 1984; Wand, Gillespie & Hedges, 1984). Vogel et al (1984) pointed out the ease of graphite formation on iron from CO₂ and H₂ mixtures at ca 600°C. The deposition reactions of carbon from the CO, H₂, and CO₂ equilibria are well known (Wagman et al, 1945) and well studied. Formation of graphite from CO₂ was discussed extensively by Boudouard (1902) and Schenck and Zimmerman (1903), and was known to chemists in France in 1851. We have used a related method, where graphite forms away from the iron, by using a higher temperature, and reduction of CO₂ to CO over Zn in the presence of H₂ (Jull et al, 1986) as an alternative to the use of Fe alone."

Nitrogens

Main resource: Chemicals/Nitrogens

"The disintegration of nitrogen by slow neutrons has been studied in photographic emulsions of different sensitivity, which enable an unambiguous distinction to be made between the emission of α-particles and protons. Evidence has been obtained that the disintegration takes place according to the reaction

¹n + ¹⁴
₇N
→ ¹⁴
₅B
+ ⁴
₂He

with a cross-section of about 10−24 cm²."

"The fast neutrons from uranium fission can be moderated by elastic collision with graphite or heavy water in a nuclear reactor until their velocity is reduced to that of thermal energies (average 2200 meters/sec= 0.025 electron volts); such very slow neutrons are called thermal neutrons. Unlike fast neutrons, whose principal reaction with matter is one of scattering, thermal neutrons because of their very low energy and velocity are more likely to be captured than scattered by the atoms they encounter. Most of the reactions of biological elements with thermal neutrons are capture reactions. After an atom captures a neutron, it forms a new compound nucleus with an excess of energy. This new compound nucleus may then:

1.) emit a gamma ray immediately to form a stable isotope, e.g.,¹

¹
₁H
+ ¹n → [²
₁H
] → ²
₁H
+ γ;

2.) emit a heavy particle immediately to form a stable isotope, e.g.,

¹⁰
₅B
+ ¹n → [¹¹
₅B
] → ⁷
₃Li
+ α;

3.) emit immediately a capture radiation to form a radioactive daughter which subsequently emits beta or gamma rays at a rate characteristic for the isotope formed, e.g.,

¹⁴
₇N
+ ¹n → [¹⁵
₇N
] → ¹⁴
₆C
* + p (half life = 6,000 years) → ¹⁴
₇N
+ β^-."

"Once produced, the ¹⁴
C quickly combines with the oxygen in the atmosphere to form carbon dioxide (CO
₂)."

Atmospheric (tropospheric or stratospheric) nitrogen is in the form of N
₂. The fusional thermal neutron creates ¹⁴N¹⁵N, which likely goes to H¹⁴C*¹⁴N (hydrogen cyanide).

The hydrogen cyanide ¹⁴N¹⁴C*H + 2O
₂ → (CO
₂) + HNO₂ (nitrous acid).

Hydrogen cyanide gas in air is explosive at concentrations over 5.6%.

Possible reactions:

1. HCN + O₂ ⟶ CO₂ + NH.
2. 4NH + O₂ ⟶ 2H₂O + 2N₂.
3. NH + O₂ ⟶ OH + NO, or HNO₂.

"Initially, the ¹⁴
C atoms get oxidized to ¹⁴
CO, primarily (Pandow et al. 1960; MacKay et al. (1963):"

1. C(g) + O₂ ⟶ CO + O: ∆H = –138.96kcal

"In the atmosphere, initially 90–100% of the ¹⁴
C produced is oxidized to ¹⁴
CO (Pandow et al. 1960)."

"In the atmosphere, the main removal process for ¹⁴
CO is oxidation by OH radicals (cf. Jockel et al. 1999). Because of the low abundance of CO in the atmosphere, and the formation of ¹⁴
CO initially, the ¹⁴
C/¹²
C ratio in the atmospheric CO is much higher than in the atmospheric CO
₂; by about two orders of magnitude in the lower stratosphere (Brenninkmeijer et al. 1995)."

Perhaps,

1. ¹⁴N¹⁴C*H + O
   ₂ → ¹⁴
   CO + HNO.

Stratospheres

The diagram shows a possible proton collision with an atmosphere molecule. Credit: SyntaxError55.{{free media}}

The stratosphere (~ 20 % by mass) and the troposphere below it contain approximately 95 % by mass of the Earth's atmosphere.

"Large air samples were collected in the lower stratosphere (10–12 km) from 43° to 85°S in June 1993, using a special compressor system. For the important trace gases CO, CH₄ and CO₂, concentration and isotopic analyses were carried out and significant correlations were discovered. The ¹⁴CO isotope is considerably in excess of tropospheric levels with very high values from 40 to 120 ¹⁴CO molecules/cm³ STP (corresponding to 12,500 percent modern carbon, at 30 ppbv), and is negatively correlated with CO. The linear relationship is used to estimate OH to be 2.9×10⁵ cm⁻³. The ¹⁸O/¹⁶O ratios for CO are the lowest ever measured and reflect the inverse kinetic isotope effect in the oxidation of CO by OH. The ¹³C/¹²C ratios for CO are not much different from tropospheric values and confirm that fractionation is small but also that the in situ contribution from CH₄ oxidation is minor. For CH₄ a correlation between δ¹³C and concentration exists from which a fractionation factor for the sink reaction (k₁₂/k₁₃) of about 1.012 is calculated, well in excess of results from laboratory experiments for OH +CH₄. The most plausible explanation presently is the removal of approximately 9% of CH₄ by Cl atoms, which, as laboratory experiments have just confirmed, induces a very large fractionation. We also reveal a linear correlation between ¹⁴CO and ¹⁴CO₂, precursor and product."

The ¹⁴
C produced by fast neutrons in the reaction ¹⁶O(n,³He)¹⁴C in the stratosphere isn't mentioned. As oxygen composes 28 % of the atmosphere, 25-28 % more ¹⁴
C is likely to be produced because fast neutrons are much more plentiful higher up.

"Spallation of atmospheric oxygen nuclei might contribute up to 20% to production of ¹⁴
C produced in the atmosphere (Lal and Peters 1967)."

Lal is an expert on in situ ¹⁴
C, otherwise known as ¹⁴
C produced by "spallation of atmospheric oxygen". I don't have access to Lal and Peters 1967. To me the phrase "might contribute up to 20% to production of ¹⁴
C produced in the atmosphere" means no one has tested the atmosphere in the stratosphere for ¹⁴
C produced by "spallation of atmospheric oxygen", but Lal and Peters know of no reason this method of producing ¹⁴
C won't occur in rough correspondence with the oxygen concentration in the stratosphere. Another way of writing it is "Spallation of atmospheric oxygen nuclei may produce up to 20% (oxygen percent of the stratosphere) of ¹⁴
C in the atmosphere."

The cross section for thermal neutron capture, in barns, for ¹⁷
O is 0.235 for the reaction ¹⁷O(n,α)¹⁴C, whereas for ¹⁴N it is 1.81 for the reaction ¹⁴N(n,p)¹⁴C. These are for the absorption of thermalized (approximately the same temperature as the gases) neutrons. The knock-on reaction for fast neutrons likely has a cross section even smaller than 0.235. This suggests that the reaction ¹⁴N(n,p)¹⁴C is about 8 times more likely to occur than the reaction ¹⁶
O(n,³
He)¹⁴
C for equal atomic concentrations, but nitrogen is 2.5 times more prevalent than oxygen. So the likely amount of ¹⁴
C produced from oxygen, which does not like neutrons like nitrogen does, may be as low or lower than 5 %. Not insignificant but small within any error analysis. If this "back-of-the-envelope" calculation is close, it would explain part of it. Lal estimates 13 such knock-on collisions on average before thermalization per neutron. That's only a 0.65 probability of success per neutron per the reaction ¹⁶
O(n,³
He)¹⁴
C. This is probably why Lal stated such knock-on reactions might produce up to 20 % of ¹⁴
C. "the main pathway" is a good compromise without experimental support. Many balloon flights have measured the main pathway production at latitudes and altitudes, but none appear to have tested the spallation reaction anywhere.

Tropospheres

The orange layer is the troposphere, the white layer is the stratosphere, and the blue layer is the mesosphere. Credit: NASA/Crew of Expedition 22.

"Since 1965 [and earlier nuclear tests] the excess of artificial ¹⁴C in the troposphere has been decreasing. The ¹⁴C that appears in the atmosphere as radioactive CO₂ disappears into the ocean and the terrestrial vegetation. Our calculation in based on a residence time for CO₂ in the atmosphere of 4–6 years. The exchange between the atmosphere and the mixed layer of the ocean occurs according to a residence time of 5–10 years. In the mixed layer of the ocean ¹⁴C is removed much faster than was earlier expected. It is assumed that ¹⁴C in this layer has reached its maximum level (10–15% above normal) and will decrease. With an assumed decrease according to a decrease coefficient of 0.1–0.05 year⁻¹ in the mixed layer, the atmospheric ¹⁴C level is calculated for further years according to a two-term exponential function. The calculation predicts that a normal ¹⁴C level in the atmosphere will be reached in about 30 years."

"Radiocarbon levels in annual plants provide a means to map out regional and continental-scale fossil fuel plumes in surface air. We collected corn (Zea mays) across North America during the summer of 2004. Plants from mountain regions of western North America showed the smallest influence of fossil fuel-derived CO₂ with a mean Δ¹⁴C of 66.3‰ ±1.7‰. Plants from eastern North America and from the Ohio-Maryland region showed a larger fossil fuel influence with a mean Δ¹⁴C of 58.8‰ ± 3.9‰ and 55.2‰ ± 2.3‰, respectively, corresponding to 2.7 ppm ± 1.5 ppm and 4.3 ppm ± 1.0 ppm of added fossil fuel CO₂ relative to the mountain west."

Dendrochronology

Main resource: Geochronology/Dendrochronology

Dates from dendrochronology can be used as a calibration and check of radiocarbon dating.

Conventional radiocarbon age

During its life, a plant or animal is in equilibrium with its surroundings by exchanging carbon either with the atmosphere, or through its diet. It will therefore have the same proportion of ¹⁴
C as the atmosphere, or in the case of marine animals or plants, with the ocean. Once it dies, it ceases to acquire ¹⁴
C, but the ¹⁴
C within its biological material at that time will continue to decay, and so the ratio of ¹⁴
C to ¹²
C in its remains will gradually decrease. Because ¹⁴
C decays at a known rate, the proportion of radiocarbon can be used to determine how long it has been since a given sample stopped exchanging carbon – the older the sample, the less ¹⁴
C will be left.

The equation governing the decay of a radioactive isotope is:

$N=N_{0}e^{-\lambda t}\,$

where N₀ is the number of atoms of the isotope in the original sample (at time t = 0, when the organism from which the sample was taken died), and N is the number of atoms left after time t. λ is a constant that depends on the particular isotope; for a given isotope it is equal to the reciprocal of the mean-life – i.e. the average or expected time a given atom will survive before undergoing radioactive decay. The mean-life, denoted by τ, of ¹⁴
C is 8,267 years, so the equation above can be rewritten as:

$t=8267\cdot \ln(N_{0}/N){\text{ years}}$

The sample is assumed to have originally had the same ¹⁴
C/¹²
C ratio as the ratio in the atmosphere, and since the size of the sample is known, the total number of atoms in the sample can be calculated, yielding N₀, the number of ¹⁴
C atoms in the original sample. Measurement of N, the number of ¹⁴
C atoms currently in the sample, allows the calculation of t, the age of the sample, using the equation above.

The half-life of a radioactive isotope (usually denoted by t_1/2) is a more familiar concept than the mean-life, so although the equations above are expressed in terms of the mean-life, it is more usual to quote the value of ¹⁴
C's half-life than its mean-life. The currently accepted value for the half-life of ¹⁴
C is 5,730 ± 40 years. This means that after 5,730 years, only half of the initial ¹⁴
C will remain; a quarter will remain after 11,460 years; an eighth after 17,190 years; and so on.

The above calculations make several assumptions, such as that the level of ¹⁴
C in the atmosphere has remained constant over time. In fact, the level of ¹⁴
C in the atmosphere has varied significantly and as a result the values provided by the equation above have to be corrected by using data from other sources. This is done by calibration curves (discussed below), which convert a measurement of ¹⁴
C in a sample into an estimated calendar age. The calculations involve several steps and include an intermediate value called the "radiocarbon age", which is the age in "radiocarbon years" of the sample: an age quoted in radiocarbon years means that no calibration curve has been used − the calculations for radiocarbon years assume that the atmospheric ¹⁴
C/¹²
C ratio has not changed over time.

Calculating radiocarbon ages also requires the value of the half-life for ¹⁴
C. In Libby's 1949 paper he used a value of 5720 ± 47 years, based on research by Engelkemeir et al. This was remarkably close to the modern value, but shortly afterwards the accepted value was revised to 5568 ± 30 years, and this value was in use for more than a decade. It was revised again in the early 1960s to 5,730 ± 40 years, which meant that many calculated dates in papers published prior to this were incorrect (the error in the half-life is about 3%). For consistency with these early papers, it was agreed at the 1962 Radiocarbon Conference in Cambridge (UK) to use the “Libby half-life” of 5568 years. Radiocarbon ages are still calculated using this half-life, and are known as "Conventional Radiocarbon Age". Since the calibration curve (IntCal) also reports past atmospheric ¹⁴
C concentration using this conventional age, any conventional ages calibrated against the IntCal curve will produce a correct calibrated age. When a date is quoted, the reader should be aware that if it is an uncalibrated date (a term used for dates given in radiocarbon years) it may differ substantially from the best estimate of the actual calendar date, both because it uses the wrong value for the half-life of ¹⁴
C, and because no correction (calibration) has been applied for the historical variation of ¹⁴
C in the atmosphere over time.

The term "conventional radiocarbon age" is also used. The definition of radiocarbon years is as follows: the age is calculated by using the following standards: a) using the Libby half-life of 5568 years, rather than the currently accepted actual half-life of 5730 years; (b) the use of an NIST standard known as HOxII to define the activity of radiocarbon in 1950; (c) the use of 1950 as the date from which years "before present" are counted; (d) a correction for fractionation, based on a standard isotope ratio, and (e) the assumption that the ¹⁴
C/¹²
C ratio has not changed over time.

Little Ice Age

Main resource: History/Recent/Little Ice Age

Changes in the ¹⁴C record, which are primarily (but not exclusively) caused by changes in solar activity, are graphed over time. Credit: Leland McInnes.{{free media}}

File:Dynamic-solar-system-the-actual-effects-of-climate-change113.JPG

The periods of highest ¹⁴C production as measured from tree rings coincide with the periods of highest cooling during the past 1200 years. Credit: Max-Planck-Institut für Aeronomie Katlenburg-Lindau.{{fairuse}}

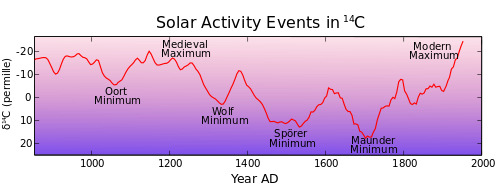
The Little Ice Age (LIA) appears to have lasted from about 1218 (782 b2k) to about 1878 (122 b2k).

The second image down shows the ¹⁴C data obtained from tree rings. The lower the solar activity, the higher the cosmic radiation, which determines the isotope content. The periods of highest ¹⁴C production as measured from tree rings coincide with the periods of highest cooling during the past 1200 years.

Late Middle Ages

The Shroud of Turin: modern photo of the face, is shown positive left, digitally processed image right. Credit: Dianelos Georgoudis.{{free media}}

The Late Middle Ages extends from about 700 b2k to 500 b2k.

Italian humanism began in the first century of the late Middle Ages (c.1350-1450).

The processed image at the right in the images on the right is the product of the application of digital filters. Digital filters are mathematical functions that do not add any information to the image, but transform it in such a way that information already present in it becomes more visible or easier to appreciate by the naked eye. The processed image was produced by inverting the brightness of the pixels in the positive image but without inverting their hue, and then by increasing both the brightness contrast and the hue saturation. Finally noise and so-called “salt and pepper” filters automatically removed the noisy information from the original image which hinders the appreciation of the actual face. To my knowledge the resulting image is the best available and indeed the only one that reveals the color information hidden in the original.

Radiocarbon dating of a corner piece of the shroud placed it between the years 1260 and 1390, in the High to Late Middle Ages, which is consistent with "its first recorded exhibition in France in 1357."

Medieval Warm Period

"A proof-of-concept self-calibrating chronology [based upon the Irish Oak chronology] clearly demonstrates that third order polynomials provide a series of statistical calibration curves that highlight lacunae in the samples."

Early Middle Ages

File:Carbon-14-chronology-lacunae.gif

Third order polynomials provide a series of statistical calibration curves that highlight lacunae in the carbon-14 samples. Credit: Gunnar Heinsohn.

File:Carbon-14-chronology.gif

The Δ¹⁴C values in a chronology can clearly be used to identify apparent catastrophic gaps and catastrophic rises in carbon-14. Credit: Gunnar Heinsohn.

The time profile of the carbon-14 spike around 774 AD. The colored dots represent the measurements in Japanese (M12) and German (Oak) trees, while the black lines represent the modeled profile corresponding to the instant production of carbon-14. Credit: Isosik.

The AD 774/5 event shows in ¹⁰Be, ¹⁴C and ³⁶Cl. Credit: Florian Mekhaldi, Raimund Muscheler, Florian Adolphi, Ala Aldahan, Jürg Beer, Joseph R. McConnell, Göran Possnert, Michael Sigl, Anders Svensson, Hans-Arno Synal, Kees C. Welten & Thomas E. Woodruff.

The Early Middle Ages date from around 1,700 to 1,000 b2k.

At left is an attempt to correlate the change in ¹⁴C with time before 1950. The different data sets are shown with different colored third order polynomial fits to each data set.

"The Δ¹⁴C values in a chronology can clearly be used to identify catastrophic gaps and catastrophic rises in carbon-14."

The first four gaps have a jump up in ¹⁴C with a fairly quick return to the calibration curve shown in the figure on the second left. However, from about 2000 b2k there is a steady rise in the Δ¹⁴C values.

The 993–994 carbon-14 spike was a rapid increase in carbon-14 content from tree rings, and followed the 774–775 carbon-14 spike. This event is also confirmed by a sharp increase of beryllium-10 and hence considered as solar-origin. It may have come from a massive solar storm as a series of auroral observations are known to be observed in late 992.

The 774–775 Carbon-14 Spike is an observed increase of 1.2% in the concentration of carbon-14 isotope in tree rings dated to the years 774 or 775 AD (1226 or 1225 b2k), which is about 20 times as high as the normal background rate of variation. It was discovered during a study of Japanese cedar trees, with the year of occurrence determined through dendrochronology. A surge in beryllium isotope ¹⁰Be, detected in Antarctic ice cores, has also been associated with the 774–775 event.

The event appears to have been global, with the same carbon-14 signal found in tree rings from Germany, Russia, the United States, and New Zealand.

The signal exhibits a sharp increase of ~1.2% followed by a slow decline (see Figure 1), which is typical for an instant production of carbon-14 in the atmosphere, indicating that the event was short in duration. The globally averaged production of carbon-14 for this event is calculated as Q = (1.1–1.5)×10⁸ atoms/cm².

Several possible causes of the event have been considered.

"This year the Northumbrians banished their king, Alred, from York at Easter-tide; and chose Ethelred, the son of Mull, for their lord, who reigned four winters. This year also appeared in the heavens a red crucifix, after sunset; the Mercians and the men of Kent fought at Otford; and wonderful serpents were seen in the land of the South-Saxons."

A "red crucifix" was recorded by the Anglo-Saxon Chronicle as appearing in the skies of Britain for the year 774; since no supernova remnant has been found for this year, it is interpreted as red Sprite lightning.

In China, there are no clear references to an aurora in the mid 770s, as happened on 762; and "comet"-sightings of the 770s do not match the expected atmospheric phenomena. Instead an anomalous "thunderstorm" was recorded for 775.

The common paradigm is that the event was caused by a solar-particle event (SPE), or a consequences of events as often happen, from a very strong solar flare(s), perhaps the strongest ever known, but still within the Sun's abilities.

Another discussed scenario of the event origin, involving a gamma-ray burst, appears unlikely, since the event was also observed in isotopes ¹⁰Be and ³⁶Cl.

The event of 774 is the strongest spike over the last 11,000 years in the record of cosmogenic isotopes, but it is not unique. A similar event occurred in 993 or 994 (1007 or 1006 b2k), but it was only 0.6 times as strong. Several other events of the same kind are also suspected to have occurred during the Holocene epoch.

From these statistics, one may expect that such strong events occur once per tens of millennia, while weaker events may occur once per millennium or even century. The event of 774 did not cause catastrophic consequences for life on Earth, but had it happened in modern times, it may have produced catastrophic damage to modern technology, particularly to communication and space-borne navigation systems. In addition, a solar flare capable of producing the observed isotopic effect would pose considerable risk to astronauts.

As of 2017, there is "little understanding" of ¹⁴C past variations because annual-resolution measurements are only available for a few periods (e.g., the AD 774-775). In 2017, another "extraordinarily large" ¹⁴C increase (20‰) has been associated with the 5480 BC event, but it is not associated with a solar event because of its long duration, but rather to an unusually fast grand minimum of solar activity.

"The Roman Climate Optimum [RCO] (sometimes called the "Roman Warm Period") [dates] ca. 200 BC--AD 150, […]. Buoyed by high levels of insolation and weak volcanic activity, the RCO was a period of warm, wet, and stable climate across much of the vast Roman Empire.⁴⁶ [The] RCO was a phase of high and stable solar activity. Between a grand solar minimum centered at 360 BC and another at 690 AD, solar radiation fluctuated within a modest band, reaching one peak at a grand maximum around AD 305.⁴⁸"

Iron Age

The iron age history period began between 3,200 and 2,100 b2k.

"After a typological analysis and a cross-dating of bronze artifacts recovered north and south of the Alps, the Roman school of Peroni set the 1020 [3020 b2k] as the beginning of the Iron Age (De Marinis 2005, p. 21; Pacciarelli 2005). The date is in agreement with the chronology supported by Lothar Sperber (Sperber 1987). The recent works of Nijboer based on the analysis of radiocarbon dates from Latial contexts agree with this high chronology (Nijboer et al. 1999-2000; Nijboer & Van der Plicht 2008; Van der Plicht et al. 2009)."

Subatlantic period

The "calibration of radiocarbon dates at approximately 2500-2450 BP [2500-2450 b2k] is problematic due to a "plateau" (known as the "Hallstatt-plateau") in the calibration curve [...] A decrease in solar activity caused an increase in production of ¹⁴C, and thus a sharp rise in Δ ¹⁴C, beginning at approximately 850 cal (calendar years) BC [...] Between approximately 760 and 420 cal BC (corresponding to 2500-2425 BP [2500-2425 b2k]), the concentration of ¹⁴C returned to "normal" values."

"The main discontinuity in the climatic condition during the Bronze Age and Iron Age transition can be identified in the boundary from Subatlantic to Subboreal (2800-2500 BP; 996/914-766/551 2σ cal. BC). Such period “has globally been identified as a time of marked climatic change. Stratigraphical, paleobotanical and archaeological evidence point to a change from a dry and warm to a more humid and cool climate in central and northwestern Europe” (Tinner et al. 2003). The climatic deterioration which characterizes this chronological range is directly responsible of the plateau in the calibration curve between 760 and 420 BC (2500-2425 BP) (see chapter 4.3.2.1). The climatic oscillation around 2700 BP (896/813 2σ cal. BC) has been detected worldwide. Van Geel et al. (1996, 1998) and Speranza et al. (2002) found an abrupt shift around 850 BC in changing species composition of peat-forming mosses in European Holocene raised bog deposits. The change was from mosses preferring warm conditions to those preferring colder and wetter environments. Archaeological evidence supports such a change. Bronze Age settlements located in the Netherlands were suddenly abandoned after a long period of occupation which last around one millennium (Dergachev et al. 2004). Other studies confirmed the climatic discontinuity; Schilman et al. (2001) studied δ18O and δ13C in deposits from the southeastern Mediterranean, off Israel, and recognized the presence of two humid events in the time ranges of 3500-3000 BP (1884/1772-1263/1215 2σ cal. BC) and 1700-1000 BP (332/389-1016/1030 2σ cal. AD) and a period of arid conditions between 3000 and 1700 BP (1263/1215 2σ cal. BC- 332/389 2σ cal. AD). Barber and Langdon (2001) identified three main long climatic deteriorations 2900-2830 BP (1119/1037-1012/934 2σ cal. BC), 2630-2590 BP (810/797-801/788 2σ cal. BC) and 1550-1400 BP (430/549-637/658 2σ cal. AD) through the analysis of plant macrofossils in a peat deposit of Walton Moss located in Northern England and comparing such data with a temperature reconstruction based on chironomids in the sediment of a nearby lake."

"Hallstatt disaster"

File:Hallstatt Plateau IntCal13 calibration curve.png

"Hallstatt disaster" refers to the plateau located in the calibration curve between 760 and 420 cal BC (2500-2425 BP). Credit: Giacomo Capuzzo.{{fairuse}}

"With the term “Hallstatt disaster” the scientific community refers to the plateau located in the calibration curve between 760 and 420 cal BC (2500-2425 BP) [the graph on the right]. The term is due to the chronological analogy to the Hallstatt society which developed in the late Bronze Age and the beginning of Iron Age in the northern part of the Alps (Austria). The flat shape of the calibration curve in this time-span is the result of the decrease, and hence the return to normal values, of the percentage of ¹⁴C after a period characterized by an increase in the concentration of radiocarbon in the atmosphere, which is mirrored in the calibration curve as a sharp descent between 850 and 760 BC (2700-2450 BP) (Speranza et al. 2000). As asserted by many authors (Van Geel et al. 1996; Van Geel et al. 1998; Tinner et al. 2003; Dergachev et al. 2004; Van der Plicht et al. 2004; Swindles et al. 2007) the chronological range 850-760 BC is characterized by an abrupt increase of the amount of ¹⁴C in the atmosphere and it corresponds chronologically to the boundary from Subatlantic to Subboreal (2800-2500 BP), which “has globally been identified as a time of marked climatic change. Stratigraphical, paleobotanical and archaeological evidence point to a change from a dry and warm to a more humid and cool climate in central and northwestern Europe” (Tinner et al. 2003)."

Subboreal period

The "period around 850-760 BC [2850-2760 b2k], characterised by a decrease in solar activity and a sharp increase of Δ ¹⁴C [...] the local vegetation succession, in relation to the changes in atmospheric radiocarbon content, shows additional evidence for solar forcing of climate change at the Subboreal - Subatlantic transition."

The "apparent reality of social equality testified by LBA urnfield burials can be definitely discarded at the Iron Age transition by the archaeological excavation at the Hexenbergle site, near Wehringen in Bayern (Germany). The monumental radiocarbon dated mound with a cremation burial of an adult male accompanied by a great amount of objects, including a sword, elements decorating a wagon and an extensive set of painted pottery (Hennig 1995). The dendrochronological date obtained on the wagon (778±5BC) provides a precise temporal location for an upper-class deceased with sepulchral paraphernalia in the Hallstatt period (Friedrich & Henning 1995, 1996)."

Late Bronze Ages

The Late Bronze Ages begin about 3550 b2k and end about 2900 b2k.

The "abandonment of lakeshore Swiss pile-dwellings has been dated to around 1520 BC [3520 b2k] (Menotti 2001). [Slightly] "later in time episodes of flood events and lake-level highstand at 3100 BP (1415/1311 2σ cal. BC) and 2800 BP (996/914 2σ cal. BC) have been recently detected in the Southern Alps, in the sediment cores extracted from the Lake Ledro, located in the province of Trento (Joannin et al. 2014)."

Radiocarbon "data indicate that the New Kingdom of Egypt started between 1570 and 1544 B.C.E [3270 - 3544 b2k]."

Middle Bronze Ages

Fresco of The Fisherman is from Akrotiri, Santorini, Greece at a height of 1.10 m. Credit: Yann Forget.{{free media}}

The Middle Bronze Ages begin about 4100 b2k and end about 3550 b2k.

The Fisherman is a Minoan Bronze Age fresco from Akrotiri, on the Aegean island of Santorini (classically Thera), dated to the Neo-Palatial period (c. 1640–1600 BC). The settlement of Akrotiri was buried in volcanic ash (dated by radiocarbon dating to c. 1627 BC [c. 3626 b2k]) by the Minoan eruption on the island, which preserved many Minoan frescoes like this.

High precision radiocarbon dating of 18 samples from Jericho, including six samples of carbonized cereal from the burnt stratum, gave the age of the strata as 1562 BC, with a margin of error of 38 years [3562 ± 38 b2k].

Atlantic period

The "Atlantic period [is] 4.6–6 ka [4,600-6,000 b2k]."

Boreal transition

File:5480 event.png

These are measured results [Δ¹⁴
C: defined in Stuiver and Polach (29)] of four series that were measured at different AMS laboratories. Credit: Fusa Miyakea, A. J. Timothy Jull, Irina P. Panyushkina, Lukas Wacker, Matthew Salzer, Christopher H. Baisan, Todd Lange, Richard Cruz, Kimiaki Masuda, and Toshio Nakamura.{{fairuse}}

"In recent years, the German oak chronology has been extended to 7938 BC [9938 b2k]. For earlier intervals, tree-ring chronologies must be based on pine, because oak re-emigrated to central Europe at the Preboreal/Boreal transition, at about 8000 BC [10,000 b2k]."

"The age range, 7145-7875 BC [9145-9875 b2k], is represented by the oak chronology, 'Main9'."

"The age range, 7833-9439 BC [9833-11439 b2k], is covered by the 1784-yr pine chronology."

In the image on the right: the upper graph shows measured results of Δ¹⁴
C: defined in Stuiver and Polach (1977) from three series at different AMS laboratories (Arizona, Nagoya, and ETH [Swiss Federal Institute of Technology]). The lower shows a comparison of bristlecone pine (diamonds), with the original datasets of the IntCal and the IntCal13 curve.

"Grand solar minima are defined as the periods when the solar activity is at a very low level, i.e., it is defined as the group sunspot number becoming less than 15 during at least two consecutive decades, according to Usoskin et al. (18). In a grand solar minimum, the ¹⁴
C content increases largely due to a reduction of the solar modulation parameter Φ. It is estimated that Φ was ∼160 MV during the Maunder Minimum, while the present-day value varies between 400 MV and 1,000 MV (19)."

"On average, the increase rate of the [Maunder, the Spörer, the Oort, the AD seventh century, and the fourth century BC] grand solar minima, where [there is] annual resolution ¹⁴
C data (5, 20–22) [of] about 0.3‰/y. Against the normal grand solar minima, the increase rate of the 5480 BC event is 2‰/y. Although the total ¹⁴
C increment of the 5480 BC event is almost equal to the other minima (∼20‰), the 5480 BC event increases much faster than the others."

"To explain a rapid and large ¹⁴
C increase, a dramatic decrease of the solar magnetism, or extreme [solar proton events] SPEs, is necessary."

"Over ∼3,000 y from ca. 6000 BC to 3000 BC, the geomagnetic dipole field was ∼0.9 times smaller than today’s field, and had an almost constant value (23)."

Hypotheses:

1. special state of the grand solar minimum,
2. successive extreme SPEs over ∼20 y, or
3. a combination of some extreme SPEs and a normal grand solar minimum (or solar magnetic activities).

Regarding hypothesis 1: "The structure of the 5480 BC event indicates a rapid increase in ¹⁴
C after 5470 BC followed by a gradual plateau-like increase for the next 15 y and then a gradual decay. Although the initial increase in ¹⁴
C for this event is different from the behavior in a normal grand solar minima, the time scale of the plateau and the following decay is consistent with the Maunder Minimum [assuming the Maunder Minimum is a standard variation of a grand solar minimum]."

Regarding hypothesis 2: It "is less likely that the plateau and the following decay can be explained by only [successive] SPEs."

It "is difficult to divide ¹⁴
C variations into the contribution by solar magnetic activities and that by SPEs".

Either "(i) several SPEs occurred during the early normal grand solar minimum, or (ii) several SPEs occurred, and then the solar magnetic activity became gradually higher."

Aassume the "SPEs only occurred in the increasing period 5481–5468 BC. Knowing that a ¹⁴
C production rate during the Maunder Minimum varies between 2.1 atoms per square centimeter per second and 2.6 atoms per square centimeter per second (19), we can accept that a production rate for the low solar magnetic activity during the increasing ¹⁴
C period is an average of upper values, 2.35 atoms per square centimeter per second. In contrast, [...] the average production rate of ¹⁴
C during normal solar magnetic activity is 1.8 atoms per square centimeter per second. Based on these hypotheses, a total ¹⁴
C production by SPEs above 2.35 and 1.8 atoms per square centimeter per second during the increase can be shown to be 6.0 ± 2.4 and 10.5 ± 3.0 atoms per square centimeter per second, respectively. The total production rate of the AD 775 event has been estimated to be 3.9 atoms per square centimeter per second to 6.9 atoms per square centimeter per second (8, 10, 11, 14). Then, it is possible that the total production by SPEs of the event is comparable to or larger than the AD 775 event."

"From direct measurements of the sun, [...] solar flares tend to occur during a solar maximum, e.g., the number of SPEs increases in solar maximum periods (27). Also, the two annual ¹⁴
C events (AD 774–775 and AD 993–994) occurred in higher solar activity periods, or at least did not occur during grand solar minimum periods (7). Thus, [hypothesis 1] (several SPEs occurred in the grand solar minimum) seems less plausible; however, the viability of one scenario over another is currently limited by our poor understanding of the mechanism for occurrence of extreme SPEs."

"In the observation of solar-type stars by the Kepler telescope, stars where several superflares occurred over several years were detected (28). Such observations of solar-type stars may support an extreme SPE origin of the 5480 BC event. Further investigations of the ¹⁴
C record, or of other radionuclides such as annual ¹⁰
Be data in ice cores, may turn up similar events, which would help to further discussion of the cause of this event. In any case, the ¹⁴
C variation of the 5480 BC event indicates an unprecedented anomaly in solar activity compared to other periods."

See also

• Dominant group/History
• Geochronology/Archaeology
• Geochronology/Cenozoic
• Geochronology/Cenozoic/Quiz
• Geochronology/Classics
• Geochronology/Dates
• Geochronology/Dendrochronology
• Geochronology/Dye 3
• Geochronology/Dye 3/Quiz
• Geochronology/Geomagnetic Polarity Time Scale
• Geochronology/Ice cores
• Geochronology/Ice cores/Black ice
• Geochronology/Ice cores/Brittle ice
• Geochronology/Ice cores/Clear ice
• Geochronology/Ice cores/Firn
• Geochronology/Ice cores/Firns
• Geochronology/Ice cores/Quiz
• Geochronology/Ice cores/Sea ice
• Geochronology/Medieval Warm Period
• Geochronology/Mesozoic
• Geochronology/Mesozoic/Quiz
• Geochronology/Middle Ages
• Geochronology/Neoglaciations
• Geochronology/Optically stimulated luminescence
• Geochronology/Paleontology
• Geochronology/Paleozoic
• Geochronology/Paleozoic/Quiz
• Geochronology/Palynology
• Geochronology/Precambrian
• Geochronology/Radiocarbon dating
• Geochronology/Radiocarbon dating/Quiz
• Geochronology/Stratigraphy
• Geochronology/Stratigraphy/Quiz
• Geochronology/Tephra layer
• Geochronology/Tephra layers
• Geochronology/Tephra layers/Quiz
• Geochronology/Uranium-thorium dating
• History of Europe to 1648
• Radiation astrohistory
• Radiocarbon dating

External links

• The SAO/NASA Astrophysics Data System

{{Anthropology resources}}

{{Humanities resources}}{{Geology resources}}