Mathematics/Astronomy

Although most of the mathematics needed to understand the information acquired through astronomical observation comes from physics, there are special needs from situations that intertwine mathematics with phenomena that may not yet have sufficient physics to explain the observations. These two uses of mathematics make mathematical astronomy a continuing challenge.
Astronomers use math all the time. One way it is used is when we look at objects in the sky with a telescope. The camera, specifically its charge-coupled device (CCD) detector, that is attached to the telescope basically converts or counts photons or electrons and records a series of numbers (the counts) - those numbers might correspond to how much light different objects in the sky are emitting, what type of light, etc. In order to be able to understand the information that these numbers contain, we need to use math and statistics to interpret them.
An initial use of mathematics in astronomy is counting entities, sources, or objects in the sky.
Objects may be counted during the daytime or night.
One use of mathematics is the calculation of distance to an object in the sky.
Notations
[edit | edit source]Notation: let the symbol indicate the Earth.
Notation: let the symbol ʘ or indicate the Sun.
Notation: let the symbol indicate the total solar irradiance.
Notation: let the symbol indicate the solar visible luminosity.
Notation: let the symbol indicate the solar bolometric luminosity.
Notation: let the symbol indicate the solar bolometric luminosity.
Notation: let the symbol represent the bolometric magnitude, the total energy output.
Notation: let the symbol represent the visual magnitude.
Notation: let the symbol indicate the solar mass.
Notation: let the symbol represent the net solar charge.
Notation: let the symbol indicate the Earth's radius.
Notation: let the symbol indicate the radius of Jupiter.
Notation: let the symbol indicate the solar radius.
Notational locations Weight Oversymbol Exponent Coefficient Variable Operation Number Range Index
For each of the notational locations around the central Variable, conventions are often set by consensus as to use. For example, Exponent is often used as an exponent to a number or variable: 2-2 or x2.
In the Notations at the top of this section, Index is replaced by symbols for the Sun (ʘ), Earth (), or can be for Jupiter (J) such as .
A common Oversymbol is one for the average .
Operation may be replaced by a function, for example.
All notational locations could look something like
bx x = n a f(x) n → ∞
where the center line means "a x Σ f(x)" for all added up values of f(x) when x = n from say 0 to infinity with each term in the sum before summation multiplied by bn, then divided by n for an average whenever n is finite.
Abstractions
[edit | edit source]A nomy (Latin nomia) is a "system of laws governing or [the] sum of knowledge regarding a (specified) field."[1] Nomology is the "science of physical and logical laws."[1]
Def. the quality of dealing with ideas rather than events is called abstraction.
Def. the act of the theoretical way of looking at things; something that exists only in idealized form is called abstraction.
Relations
[edit | edit source]Notation: let the relation symbol ≠ indicate that two expressions are different.
For example, 2 x 3 ≠ 5 x 7.
Notation: let the relation symbol ~ represent similar to.
For example, depending on the scale involved, 7 ~ 8 on a scale of 10, 7/10 = 0.7 and 8/10 = 0.8. relative to numbers between 0.5 and 1.0, 0.7 ~ 0.8, but 0.2 ≁ 0.7.
Similarity may be close such as 0.7 ≈ 0.8, but 0.5 ~ 0.8. Or similarity may include equality, 5 ± 3 ≃ 4 ± 2. When the degree of equality is greater than the degree of similarity, the symbol ≅ is used. The reverse is represented by ≊.
Differences
[edit | edit source]Here's a theoretical definition:
Def. an abstract relation between identity and sameness is called a difference.
Notation: let the symbol represent difference in.
Order
[edit | edit source]Ordering numbers may mean listing them in increasing value. For example, 2 is less than 3 so that in increasing order 2,3 is the list.
Notation: let the symbol > represent greater than.
For example, the integer five (5) is greater than the integer (2): 5 > 2.
Notation: let the symbol < represent less than.
For, example, 2 < 3.
Numbers
[edit | edit source]
Scientific notation (more commonly known as standard form) is a way of writing numbers that are too big or too small to be conveniently written in decimal form. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians and engineers.
| Standard decimal notation | Normalized scientific notation |
|---|---|
| 2 | 2×100 |
| 300 | 3×102 |
| 4,321.768 | 4.321768×103 |
| -53,000 | −5.3×104 |
| 6,720,000,000 | 6.72×109 |
| 0.2 | 2×10−1 |
| 0.000 000 007 51 | 7.51×10−9 |
A metric prefix or SI prefix is a unit prefix that precedes a basic unit of measure to indicate a decadic multiple or fraction of the unit. Each prefix has a unique symbol that is prepended to the unit symbol.
| Metric prefixes | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A significant figure is a digit in a number that adds to its precision. This includes all nonzero numbers, zeroes between significant digits, and zeroes indicated to be significant.
Leading and trailing zeroes are not significant because they exist only to show the scale of the number. Therefore, 1,230,400 has five significant figures—1, 2, 3, 0, and 4; the two zeroes serve only as placeholders and add no precision to the original number.
When a number is converted into normalized scientific notation, it is scaled down to a number between 1 and 10. All of the significant digits remain, but all of the place holding zeroes are incorporated into the exponent. Following these rules, 1,230,400 becomes 1.2304 x 106.
It is customary in scientific measurements to record all the significant digits from the measurements, for example, 1,230,400, but the measurement may have introduced an error which when calculated indicates the last significant digit has a range of values where the most likely one is the "4". The range may be 3-5 so that the last significant digit plus this error may be written as (4,1) meaning 4-1=3 and 4+1=5.
Another example of significant digits is the speed of all massless particles and associated fields—including electromagnetic radiation such as light—in vacuum ... [The most accurate value is] 299792.4562±0.0011 [km/s].[2] The magnitude of the speed is 299792.4562 and the actual measured variation is ±0.0011 so that the last two significant digits "62" are most likely within a variation from "51" to "73".
Most calculators and many computer programs present very large and very small results in E notation. The letter E or e is often used to represent times ten raised to the power of (which would be written as "x 10b") [where b represents a number] and is followed by the value of the exponent.
Def. any real number that cannot be expressed as a ratio of two integers is called an irrational number.
Def. incapable of being put into one-to-one correspondence with the natural numbers or any subset thereof is called uncountable.
An uncountable set of numbers such as the irrational numbers lies somewhere between a finite set of numbers, for example, the set of natural factors of 6: {1,2,3,6}, and an infinite set of numbers such as the natural numbers.
Def. the branch of pure mathematics concerned with the properties of integers is called number theory.
Arithmetics
[edit | edit source]Arithmetic involves the manipulation of numbers.
Theory of arithmetic
[edit | edit source]Def. the mathematics of numbers (integers, rational numbers, real numbers, or complex numbers) under the operations of addition, subtraction, multiplication, and division is called an arithmetic.
Def. a symbol ( = ) used in mathematics to indicate that two values are the same is called equals, or equal to.
Consider the integers: 1 and 2. The statement, "1 + 2 = 3", contains the operation + (addition) and the relation = (equals).
Exponentials
[edit | edit source]The exponential can require a different operator of arithmetic.
The number is an important mathematical constant, approximately equal to 2.71828, that is the base of the natural logarithm.[3]
- e2 + e3 ≠ e5. Yet
- e2 x e3 = e(2 + 3) = e5.
Logarithms
[edit | edit source]Def. For a number [...], the [exponent or power] to which a given base number must be raised in order to obtain [the number] is called a logarithm.
Consider 103, the base number is 10. The exponent is 3. The number itself is 1000. Using logarithm notation
For 24,
For e4,
Notation: let the symbol dex represent the difference between powers of ten.
An order or factor of ten, dex is used both to refer to the function and the number of (possibly fractional) orders of magnitude separating two numbers. When dealing with log to the base 10 transform of a number set, the transform of 10, 100, and 1 000 000 is , , and , so the difference between 10 and 100 in base 10 is 1 dex and the difference between 1 and 1 000 000 is 6 dex.
Mathematics
[edit | edit source]Def. an abstract representational system used in the study of numbers, shapes, structure and change and the relationships between these concepts is called mathematics.
Def. the branches of mathematics used in the study of astronomy, astrophysics and cosmology is called astromathematics.
Changes
[edit | edit source]Def. the act or instance of making, or the process of becoming different is called change.
Revolutions
[edit | edit source]Def. the traversal of one body through an orbit around another body is called a revolution.
Operations
[edit | edit source]However, attempting to add 1 dome to 1 telescope may have little or no meaning. The operation of addition would be similar to the operation of construction.
If 1 G2V star is added to 1 M2V star the result may be a double star. The operation of addition here usually requires an explanation (a theory). Astronomers use math all the time. One way it is used is when we look at objects in the sky with a telescope. The camera that is attached to the telescope basically records a series of numbers - those numbers might correspond to how much light different objects in the sky are emitting, what type of light, etc. In order to be able to understand the information that these numbers contain, we need to use math and statistics to interpret them.
Inclinations
[edit | edit source]
Def. the angle of intersection of a reference plane is called an inclination.
"The orbital inclination [i] [of Mercury] varies between 5° and 10° with a 106 yr period with smaller amplitude variations with a period of about 105 yr."[4]
Dimensional analyses
[edit | edit source]Def. a single aspect of a given thing is called a dimension.
Usually, in astronomy, a number is associated with a dimension or aspect of an entity. For example, the Earth is 1.50 x 108 km on average from the Sun. Kilometer (km) is a dimension and 1.50 x 108 is a number.
Def. the study of the dimensions of quantities; used to obtain information about large complex systems, and as a means of checking equations is called dimensional analysis.
Prefixed values cannot be multiplied or divided together, and they have to be converted into non-prefixed standard form for such calculations. For example, 5 mV × 5 mA ≠ 25 mW. The correct calculation is: 5 mV × 5 mA = 5 × 10−3 V × 5 × 10−3 A = 25 x 10−6 W = 25 µW = 0.025 mW.
Prefixes corresponding to an exponent that is divisible by three are often recommended. Hence "100 m" rather than "1 hm" (hectometre) or "10 dam" (decametres). The "non-three" prefixes (hecto-, deca-, deci-, and centi-) are however more commonly used for everyday purposes than in science.
When units occur in exponentiation, for example, in square and cubic forms, any size prefix is considered part of the unit, and thus included in the exponentiation.
- 1km2 means one square kilometre or the size of a square of 1000 m by 1000 m and not 1000 square metres.
- 2Mm3 means two cubic megametre or the size of two cubes of 1000000m by 1000000m by 1000000m or 2×1018 m3, and not 2000000cubic metres (2×106 m3).
- Examples
- 5 cm = 5×10−2 m = 5×0.01m = 0.05m
- 3 MW = 3×106 W = 3×1000000W = 3000000W
Astronomical units
[edit | edit source]Def. "1 day (d)" is called the astronomical unit of time.[5]
Def. "the distance from the centre of the Sun at which a particle of negligible mass, in an unperturbed circular orbit, would have an orbital period of 365.2568983 days" is called the Astronomical Unit (AU).[5]
Def. "the distance at which one Astronomical Unit subtends an angle of one arcsecond" is called the parsec (pc).[5]
Def. "365.25 days" is called a Julian year.[5]
Def. "36,525 days" is called a Julian century.[5]
| Dimension | Astronomy | Symbol | Physics | Symbol | Conversion |
|---|---|---|---|---|---|
| time | 1 day | d | 1 second | s | 1 d = 86,400 s[5] |
| time | 1 "Julian year"[6] | J | 1 second | s | 1 J = 31,557,600 s |
| distance | 1 astronomical unit | AU | 1 meter | m | 1 AU = 149,597,870.691 km[5] |
| mass | 1 Sun | Mʘ | 1 kilogram | kg | 1 Mʘ = 1.9891 x 1030 kg[5] |
| luminosity | 1 Sun | Lʘ | 1 watt | W | 1 Lʘ = 3.846 x 1026 W[7] |
| angular distance | 1 parsec | pc | 1 meter | m | 1 pc ~ 30.857 x 1012 km[5] |
Regions
[edit | edit source]
A region is a division or part of a space having definable characteristics but not always fixed boundaries.
Def. any considerable and connected part of a space or surface; specifically, a tract of land or sea of considerable but indefinite extent; a country; a district; in a broad sense, a place without special reference to location or extent but viewed as an entity for geographical, social or cultural reasons is called a region.
Region is most commonly found as a term used in terrestrial and astrophysics sciences also an area, notably among the different sub-disciplines of geography, studied by regional geographers. Regions consist of subregions that contain clusters of like areas that are distinctive by their uniformity of description based on a range of statistical data, for example demographic, and locales.
Def. a subset of that is open (in the standard Euclidean topology), connected and non-empty is called a region, or region of , where is the n-dimensional real number system.
Areas
[edit | edit source]
In the figure on the right, an area is the difference in the x-direction times the difference in the y-direction.
This rectangle cornered at the origin of the curvature represents an area for the curve.
Orbits
[edit | edit source]
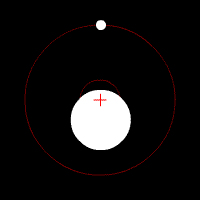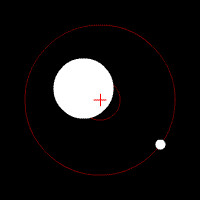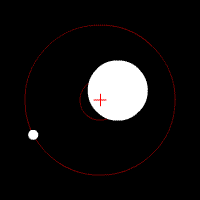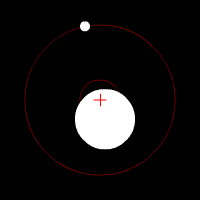


Def. a circular or elliptical path of one object around another object is called an orbit.
Historically, the apparent motions of the planets were first understood geometrically (and without regard to gravity) in terms of epicycles, which are the sums of numerous circular motions.[8] Theories of this kind predicted paths of the planets moderately well, until Johannes Kepler was able to show that the motions of planets were in fact (at least approximately) elliptical motions.[9]
In the geocentric model of the solar system, the celestial spheres model was originally used to explain the apparent motion of the planets in the sky in terms of perfect spheres or rings, but after the planets' motions were more accurately measured, theoretical mechanisms such as deferent and epicycles were added. Although it was capable of accurately predicting the planets' position in the sky, more and more epicycles were required over time, and the model became more and more unwieldy.
In theoretical astronomy, whether the Earth moves or not, serving as a fixed point with which to measure movements by objects or entities, or there is a solar system with the Sun near its center, is a matter of simplicity and calculational accuracy. Copernicus's theory provided a strikingly simple explanation for the apparent retrograde motions of the planets—namely as parallactic displacements resulting from the Earth's motion around the Sun—an important consideration in Johannes Kepler's conviction that the theory was substantially correct.[10] "[Kepler] knew that the tables constructed from the heliocentric theory were more accurate than those of Ptolemy"[10] with the Earth at the center. Using a computer, this means that for competing programs, one written for each theory, the heliocentric program finishes first (for a mutually specified high degree of accuracy).
Orbits come in many shapes and motions. The simplest forms are a circle or an ellipse.
Infinitesimals
[edit | edit source]Notation: let the symbol represent an infinitesimal difference in.
Notation: let the symbol represent an infinitesimal difference in one of more than one.
Distances
[edit | edit source]
Def. the amount of space between two points, usually geographical points, usually (but not necessarily) measured along a straight line is called a distance.
Distance (or farness) is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria (e.g. "two counties over"). In mathematics, a distance function or metric is a generalization of the concept of physical distance. A metric is a function that behaves according to a specific set of rules, and provides a concrete way of describing what it means for elements of some space to be "close to" or "far away from" each other.
Def.
- a series of interconnected rings or links usually made of metal,
- a series of interconnected links of known length, used as a measuring device,
- a long measuring tape,
- a unit of length equal to 22 yards. The length of a Gunter's surveying chain. The length of a cricket pitch. Equal to 20.12 metres. Equal to 4 rods. Equal to 100 links.
- a totally ordered set, especially a totally ordered subset of a poset,
- iron links bolted to the side of a vessel to bold the dead-eyes connected with the shrouds; also, the channels, or
- the warp threads of a web
is called a chain.
Def. a unit of length equal to 220 yards or exactly 201.168 meters, now only used in measuring distances in horse racing is called a furlong.
Def.
- a trench cut in the soil, as when plowed in order to plant a crop or
- any trench, channel, or groove, as in wood or metal
is called a furrow.
Def. the distance that a person can walk in one hour, commonly taken to be approximately three English miles (about five kilometers) is called a league.
Then,
Cosmic distance ladders
[edit | edit source]The apparent magnitude, or the magnitude as seen by the observer, can be used to determine the distance D to the object in kiloparsecs (where 1 kpc equals 1000 parsecs) as follows:
where m the apparent magnitude and M the absolute magnitude.
Diameters
[edit | edit source]Def. the length of any straight line between two points on the circumference of a circle that passes through the centre/center of the circle is called a diameter.
Arithmetic dimensional analysis
[edit | edit source]Usually, pure arithmetic only involves numbers. But, when arithmetic is used in a science such as radiation astronomy, dimensional analysis is also applicable.
To build an observatory usually requires adding components together.
For example: 1 dome + 1 telescope + 1 outbuilding + 1 control room + 1 laboratory + 1 observation room may = 1 observatory.
Yet,
- 1 + 1 + 1 + 1 + 1 + 1 = 6 components in 1 simple observatory.
Obliquities
[edit | edit source]Def. the quality of being oblique in direction, deviating from the horizontal or vertical; or the angle created by such a deviation is called obliquity.
Axial tilt (also called obliquity) is the angle between an object's rotational axis, and a line perpendicular to its orbital plane. The planet Venus has an axial tilt of 177.3° because it is rotating in retrograde direction, opposite to other planets like Earth. The planet Uranus is rotating on its side in such a way that its rotational axis, and hence its north pole, is pointed almost in the direction of its orbit around the Sun. Hence the axial tilt of Uranus is 97°.[11]
The obliquity of the Earth's axis has a period of about 41,000 years.[12]
Inverses
[edit | edit source]Def. the set of points that map to a given point (or set of points) under a specified function is called an inverse image.
Under the function given by , the inverse image of 4 is , as is the inverse image of .
Antapex
[edit | edit source]Def. the point to which the Sun appears to be moving with respect to the local stars is called the solar apex.
An antapex is a point that an astronomical object's total motion is directed away from. It is opposite to the apex.
The local standard of rest or LSR follows the mean motion of material in the Milky Way in the neighborhood of the Sun.[13] The path of this material is not precisely circular.[14] The Sun follows the solar circle (eccentricity e < 0.1 ) at a speed of about 220 km/s in a clockwise direction when viewed from the galactic north pole at a radius of ≈ 8 kpc about the center of the galaxy near Sgr A*, and has only a slight motion, towards the solar apex, relative to the LSR.[15] The Sun's peculiar motion relative to the LSR is 13.4 km/s.[16][17] The LSR velocity is anywhere from 202–241 km/s.[18]
Algebras
[edit | edit source]Notation: let the symbol * designate an as yet unspecified operation.
Notation: let the symbol R designate an as yet unspecified relation.
Def. a system for computation using letters or other symbols to represent numbers, with rules for manipulating these symbols is called an algebra.
Fundamentally, algebra uses letters to represent as yet unspecified numbers. The numbers may be integers, rational numbers, irrational numbers, or any real number or complex number. As an experimentalist, eventually you must find a way to change unspecified numbers into specified ones. But, as a theoretician, first you are free to leave the numbers in some algebraic form, then to have your theory tested by any experimentalist you need to relate the algebraic terms of your theory to real or complex numbers.
Consider the lower case letters of the English alphabet: a and n. The statement, "a * n R an", contains the operation * (followed by) and the relation R (spells the word).
The manipulations of these symbols are performed using operations.
Def. a procedure for generating a value from one or more other values (the operands; the value for any particular [operand] is unique) is called an operation.
Notation: let the symbol represent the summation of many terms.
Notation: let the symbol represent the product of many terms.
The results are recorded using statements of relation.
Def. a relation in which each element of the domain is associated with exactly one element of the codomain is called a function.
Geometries
[edit | edit source]
Def. of geometrical figures including triangles, squares, ellipses, arcs and more complex figures, having the same shape but possibly different size, rotational orientation, and position; in particular, having corresponding angles equal and corresponding line segments proportional; such that one can be had from the other using a sequence of operations of rotation, translation and scaling is called similar.
Def. a branch of mathematics that studies solutions of systems of algebraic equations using both algebra and geometry is called algebraic geometry.
Def. a branch of mathematics that investigates properties of figures through the coordinates of their points is called analytic geometry.
Def. a branch of mathematics that investigates those properties of figures that are invariant when projected from a point to a line or plane is called projective geometry.
Def. a set along with a collection of finitary functions and relations is called a structure.
Def.
- a set of points with some added structure,
- distance between things,
- physical extent a range of values or locations across two or three dimensions,
- physical extent in all directions, seen as an attribute of the universe,
- a set of points, each of which is uniquely specified by a number (the dimensionality) of coordinates,
- a generalized construct or set whose members have some property in common; typically there will be a geometric metaphor allowing these members to be viewed as "points",
- a gap; an empty place,
- a (chiefly empty) area or volume with set limits or boundaries,
is called a space.
The universe as often perceived may be described spatially, sometimes with plane geometry, other occasions with spherical geometry.
Coordinates
[edit | edit source]
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the [positive and negative numbers] signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0,0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.
Triclinic coordinates
[edit | edit source]
A triclinic coordinate system has coordinates of different lengths (a ≠ b ≠ c) along x, y, and z axes, respectively, with interaxial angles that are not 90°. The interaxial angles α, β, and γ vary such that (α ≠ β ≠ γ). These interaxial angles are α = y⋀z, β = z⋀x, and γ = x⋀y, where the symbol "⋀" means "angle between".
Monoclinic coordinates
[edit | edit source]
In a monoclinic coordinate system, a ≠ b ≠ c, and depending on setting α = β = 90° ≠ γ, α = γ = 90° ≠ β, α = 90° ≠ β ≠ γ, or α = β ≠ γ ≠ 90°.
Orthorhombic coordinates
[edit | edit source]
In an orthorhombic coordinate system α = β = γ = 90° and a ≠ b ≠ c.
Tetragonal coordinates
[edit | edit source]
A tetragonal coordinate system has α = β = γ = 90°, and a = b ≠ c.
Rhombohedral coordinates
[edit | edit source]
A rhombohedral system has a = b = c and α = β = γ < 120°, ≠ 90°.
Hexagonal coordinates
[edit | edit source]
A hexagonal system has a = b ≠ c and α = β = 90°, γ = 120°.
Triangles
[edit | edit source]
Def. a polygon with three sides and three angles is called a triangle.
Curvatures
[edit | edit source]The graph at the top of areas shows a curve or curvature.
Conic sections
[edit | edit source]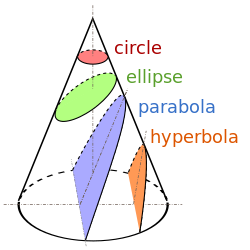

Def. any of the four distinct shapes that are the intersections of a cone with a plane, namely the circle, ellipse, parabola and hyperbola is called a conic section.
In mathematics, a conic section (or just conic) is a curve obtained as the intersection of a cone (more precisely, a right circular conical surface) with a plane.
Various parameters are associated with a conic section, as shown in the following table. (For the ellipse, the table gives the case of a>b, for which the major axis is horizontal; for the reverse case, interchange the symbols a and b. For the hyperbola the east-west opening case is given. In all cases, a and b are positive.)
| conic section | equation | eccentricity (e) | linear eccentricity (c) | semi-latus rectum (ℓ) | focal parameter (p) |
|---|---|---|---|---|---|
| circle | |||||
| ellipse | |||||
| parabola | |||||
| hyperbola |
The general parabola equation with a vertical axis
is solved in terms of the constants a, b, and c for x by
The general conic equation in a Cartesian plane (x,y) is
where
For parabolas,
where A and C are not both zero.
Variations
[edit | edit source]Def. a partial change in the form, position, state, or qualities of a thing or a related but distinct thing is called a variation.
Precessions
[edit | edit source]Def. any of several slow changes in an astronomical body's rotational or orbital parameters such as the slow gyration of the Earth’s axis around the pole of the ecliptic is called a precession.
Def. the slow westward shift of the equinoxes along the plane of the ecliptic, resulting from precession of an object's axis of rotation, and causing the equinoxes to occur earlier each year is called the precession of the equinoxes.
The equinoxes of Earth precess with a period of about 21,000 years.[12]
Rotations
[edit | edit source]
Def. the act of turning around a centre or an axis is called a rotation.
A rotation is a circular movement of an object around a center (or point) of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation about an external point, e.g. the Earth about the Sun, is called a revolution or orbital revolution.
Axes of rotation can be multiple:
- one-fold - ⨀, ⦺, ⧀
- two-fold - ⨸,
- three-fold - ▲,
- four-fold - ◈,
- five-fold - ✪, or
- six-fold - ✱.
Higher-fold axes of rotation are possible. As the number-fold of axes increases, the polyhedron approaches a circle. Or, in three dimensions, a sphere.
Mirror planes
[edit | edit source]A mirror plane reflects on the other side the handedness that is on the initial side:
- ⨴ | ⨵, the plane between is the mirror so that on either side is the reflection of the other, here an axis of rotation out of the plane of the paper could place the reflection on top of the object on the other side of the mirror plane,
- ∀ | ∀, here such an axis of rotation would not work,
- ⊆ | ⊇, this one is like number two,
- ⊕ | ⊕, here rotational symmetry is preserved, and
- ⨫ | ⨬, here rotation axes exist in the plane of the paper.
Resonances
[edit | edit source]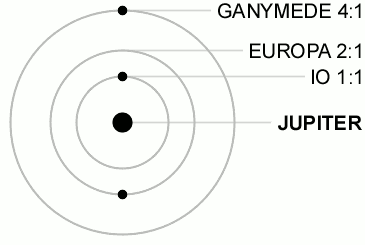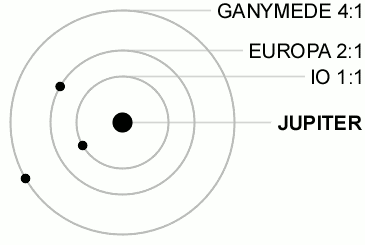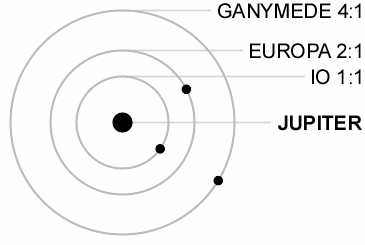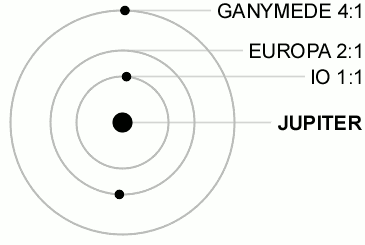
An orbital resonance occurs when two orbiting bodies exert a regular, periodic gravitational influence on each other, usually due to their orbital periods being related by a ratio of two small integers. The physics principle behind orbital resonance is similar in concept to pushing a child on a swing, where the orbit and the swing both have a natural frequency, and the other body doing the "pushing" will act in periodic repetition to have a cumulative effect on the motion. Orbital resonances greatly enhance the mutual gravitational influence of the bodies, i.e., their ability to alter or constrain each other's orbits. In most cases, this results in an unstable interaction, in which the bodies exchange momentum and shift orbits until the resonance no longer exists. Under some circumstances, a resonant system can be stable and self-correcting, so that the bodies remain in resonance. Examples are the 1:2:4 resonance of Jupiter's moons Ganymede, Europa and Io, and the 2:3 resonance between Pluto and Neptune. Unstable resonances with Saturn's inner moons give rise to gaps in the rings of Saturn. The special case of 1:1 resonance (between bodies with similar orbital radii) causes large Solar System bodies to eject most other bodies sharing their orbits; this is part of the much more extensive process of clearing the neighbourhood, an effect that is used in the current definition of a planet.
Eccentricities
[edit | edit source]Def. the ratio, constant for any particular conic section, of the distance of a point from the focus to its distance from the directrix is called the eccentricity.
For an ellipse, the eccentricity is the ratio of the distance from the center to a focus divided by the length of the semi-major axis.
"Mercury's orbit eccentricity [e] varies between about 0.11 and 0.24 with the shortest time lapse between the extremes being about 4 x 105 yr".[4] "Smaller amplitude variations occur with about a 105 yr period."[4]
Spherical geometries
[edit | edit source]
Def. the non-Euclidean geometry on the surface of a sphere is called spherical geometry.
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy.
A sphere [suggested by the image of the Earth at right] is not a Euclidean space, but locally the laws of the Euclidean geometry are good approximations. In a small triangle on the face of the earth, the sum of the angles is very nearly 180. The surface of a sphere can be represented by a collection of two dimensional maps. Therefore it is a two dimensional manifold.
The great-circle or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere (as opposed to going through the sphere's interior). Because spherical geometry is different from ordinary Euclidean geometry, the equations for distance take on a different form. The distance between two points in Euclidean space is the length of a straight line from one point to the other. On the sphere, however, there are no straight lines. In non-Euclidean geometry, straight lines are replaced with geodesics. Geodesics on the sphere are the great circles (circles on the sphere whose centers are coincident with the center of the sphere).
Through any two points on a sphere which are not directly opposite each other, there is a unique great circle. The two points separate the great circle into two arcs. The length of the shorter arc is the great-circle distance between the points. A great circle endowed with such a distance is the Riemannian circle.
Logical laws
[edit | edit source]
Kepler's laws of planetary motion:
- The orbit of every planet is an ellipse with the Sun at one of the two foci.
- A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.[19]
- The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
The diagram at the right illustrates Kepler's three laws of planetary orbits: (1) The orbits are ellipses, with focal points ƒ1 and ƒ2 for the first planet and ƒ1 and ƒ3 for the second planet. The Sun is placed in focal point ƒ1. (2) The two shaded sectors A1 and A2 have the same surface area and the time for planet 1 to cover segment A1 is equal to the time to cover segment A2. (3) The total orbit times for planet 1 and planet 2 have a ratio a13/2 : a23/2.
The simplest description of the paths astronomical objects may take when passing each other includes a hyperbolic and parabolic pass. When capture occurs it usually produces an elliptical orbit.
Horizontal coordinate system
[edit | edit source]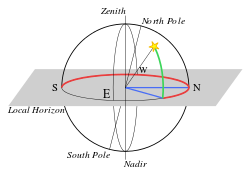
The altitude of an entity in the sky is given by the angle of the arc from the local horizon to the entity.
The horizontal coordinate system is a celestial coordinate system that uses the observer's local horizon as the fundamental plane. This coordinate system divides the sky into the upper hemisphere where objects are visible, and the lower hemisphere where objects cannot be seen since the earth is in the way. The great circle separating hemispheres [is] called [the] celestial horizon or rational horizon. The pole of the upper hemisphere is called the zenith. The pole of the lower hemisphere is called the nadir.[20]
The horizontal coordinates are:
- Altitude (Alt), sometimes referred to as elevation, is the angle between the object and the observer's local horizon. It is expressed as an angle between 0 degrees to 90 degrees.
- Azimuth (Az), that is the angle of the object around the horizon, usually measured from the north increasing towards the east.
- Zenith distance, the distance from directly overhead (i.e. the zenith) is sometimes used instead of altitude in some calculations using these coordinates. The zenith distance is the complement of altitude (i.e. 90°-altitude).
Fixed point in the sky
[edit | edit source]

The observations require precise measurement and adaptations to the movements of the Earth, especially when and where, for a time, an object or entity is available.
With the creation of a geographical grid, an observer needs to be able to fix a point in the sky. From many observations within a period of stability, an observer notices that patterns of visual objects or entities in the night sky repeat. Further, a choice is available: is the Earth moving or are the star patterns moving? Depending on latitude, the observer may have noticed that the days vary in length and the pattern of variation repeats after some number of days and nights. By choosing an equal day/night position among the fixed objects in the night sky, the observer can measure equatorial coordinates: declination (Dec) and right ascension (RA).
Once these can be determined, the apparent absolute positions of objects or entities are available in a communicable form. The repeat pattern of (day/night)s allows the observer to calculate the RA and Dec at any point during the cycle for a new object, or approximations are made using RA and Dec for recognized objects.
Independent of the choice made (Earth moves or not), the pattern of objects is the same for days or nights of the repeating length once a year. The vernal equinox is a day/night of equal length and the same pattern of objects in the night sky. The autumnal equinox is the other equal length day/night with its own pattern of objects in the night sky.
The projection of the Earth's equator and poles of rotation, or if the observer hasn't concluded as yet that it's the Earth that's rotating, the circulating pattern of stars in ever smaller circles heading in specific directions, is the celestial sphere.
Trigonometries
[edit | edit source]Def. the relationships between the sides and the angles of triangles and the calculations based on them is called trigonometry.
Trigonometry ... studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves.
Angular displacement
[edit | edit source]For the speeds in units of c, β = v/c, "[i]n the usual interpretation of superluminal motion, the apparent velocity is given by
where βjetc is the jet velocity, and the jet makes an angle Φ to the line of sight."[21]
Radius of the Earth
[edit | edit source]Because the Earth is not perfectly spherical, no single value serves as its natural radius. Earth radius is used as a unit of distance, especially in astronomy and geology. Any radius a distance from a point on the surface to the center falls between the polar minimum of about 6,357 km and the equatorial maximum of about 6,378 km (≈3,950 – 3,963 mi).
Equations for great-circle distance can be used to roughly calculate the shortest distance between points on the surface of the Earth (as the crow flies), and so have applications in navigation.
Let be the geographical latitude and longitude of two points (a base "standpoint" and the destination "forepoint"), respectively, and their absolute differences; then , the central angle between them, is given by the spherical law of cosines:
The distance d, i.e. the arc length, for a sphere of radius r and given in
This arccosine formula above can have large rounding errors if the distance is small (if the two points are a kilometer apart the cosine of the central angle comes out 0.99999999). An equation known as the haversine formula is numerically better-conditioned for small distances:[22]
A formula that is accurate for all distances is the following special case (a sphere, which is an ellipsoid with equal major and minor axes) of the Vincenty formula (which more generally is a method to compute distances on ellipsoids):[23]
When programming a computer, one should use the atan2() function rather than the ordinary arctangent function (atan()), in order to simplify handling of the case where the denominator is zero, and to compute unambiguously in all quadrants. Also, make sure that all latitudes and longitudes are in radians (rather than degrees) if that is what your programming language's sin(), cos() and atan2() functions expect (1 radian = 180 / π degrees, 1 degree = π / 180 radians).
Distance computation
[edit | edit source]
Distance measurement by parallax is a special case of the principle of triangulation, which states that one can solve for all the sides and angles in a network of triangles if, in addition to all the angles in the network, the length of at least one side has been measured. Thus, the careful measurement of the length of one baseline can fix the scale of an entire triangulation network. In parallax, the triangle is extremely long and narrow, and by measuring both its shortest side (the motion of the observer) and the small top angle (always less than 1 arcsecond,[24] leaving the other two close to 90 degrees), the length of the long sides (in practice considered to be equal) can be determined.
Assuming the angle is small (see derivation below), the distance to an object (measured in parsecs) is the reciprocal of the parallax (measured in arcseconds): For example, the distance to Proxima Centauri is 1/0.7687=1.3009 parsecs (4.243 ly).[25]
Distance to the Moon
[edit | edit source]Any distance to the Moon is often initially calculated as a multiple of the Earth radius .
Parallaxes
[edit | edit source]Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines."[26]"Astron. Apparent displacement, or difference in the apparent position, of an object, caused by actual change (or difference) of position of the point of observation; spec. the angular amount of such displacement or difference of position, being the angle contained between the two straight lines drawn to the object from the two different points of view, and constituting a measure of the distance of the object."[27]
Nearby objects have a larger parallax than more distant objects when observed from different positions, so parallax can be used to determine distances.
Astronomers use the principle of parallax to measure distances to celestial objects including to the Moon, the Sun, and to stars beyond the Solar System.
Diurnal parallax
[edit | edit source]Diurnal parallax is a parallax that varies with rotation of the Earth or with difference of location on the Earth. The Moon and to a smaller extent the terrestrial planets or asteroids seen from different viewing positions on the Earth (at one given moment) can appear differently placed against the background of fixed stars."[28][29]
Lunar parallax
[edit | edit source]

Lunar parallax (often short for lunar horizontal parallax or lunar equatorial horizontal parallax), is a special case of (diurnal) parallax: the Moon, being the nearest celestial body, has by far the largest maximum parallax of any celestial body, it can exceed 1 degree.[30]
The diagram (above) for stellar parallax can illustrate lunar parallax as well, if the diagram is taken to be scaled right down and slightly modified. Instead of 'near star', read 'Moon', and instead of taking the circle at the bottom of the diagram to represent the size of the Earth's orbit around the Sun, take it to be the size of the Earth's globe, and of a circle around the Earth's surface. Then, the lunar (horizontal) parallax amounts to the difference in angular position, relative to the background of distant stars, of the Moon as seen from two different viewing positions on the Earth:- one of the viewing positions is the place from which the Moon can be seen directly overhead at a given moment (that is, viewed along the vertical line in the diagram); and the other viewing position is a place from which the Moon can be seen on the horizon at the same moment (that is, viewed along one of the diagonal lines, from an Earth-surface position corresponding roughly to one of the blue dots on the modified diagram).
The lunar (horizontal) parallax can alternatively be defined as the angle subtended at the distance of the Moon by the radius of the Earth[31] -- equal to angle p in the diagram when scaled-down and modified as mentioned above.
The lunar horizontal parallax at any time depends on the linear distance of the Moon from the Earth. The Earth-Moon linear distance varies continuously as the Moon follows its perturbed and approximately elliptical orbit around the Earth. The range of the variation in linear distance is from about 56 to 63.7 earth-radii, corresponding to horizontal parallax of about a degree of arc, but ranging from about 61.4' to about 54'.[30] The Astronomical Almanac and similar publications tabulate the lunar horizontal parallax and/or the linear distance of the Moon from the Earth on a periodical e.g. daily basis for the convenience of astronomers (and formerly, of navigators), and the study of the way in which this coordinate varies with time forms part of lunar theory.
Parallax can also be used to determine the distance to the Moon.
One way to determine the lunar parallax from one location is by using a lunar eclipse. A full shadow of the Earth on the Moon has an apparent radius of curvature equal to the difference between the apparent radii of the Earth and the Sun as seen from the Moon. This radius can be seen to be equal to 0.75 degree, from which (with the solar apparent radius 0.25 degree) we get an Earth apparent radius of 1 degree. This yields for the Earth-Moon distance 60 Earth radii or 384,000 km. This procedure was first used by Aristarchus of Samos[32] and Hipparchus, and later found its way into the work of Ptolemy. The diagram at right shows how daily lunar parallax arises on the geocentric and geostatic planetary model in which the Earth is at the centre of the planetary system and does not rotate. It also illustrates the important point that parallax need not be caused by any motion of the observer, contrary to some definitions of parallax that say it is, but may arise purely from motion of the observed.
Another method is to take two pictures of the Moon at exactly the same time from two locations on Earth and compare the positions of the Moon relative to the stars. Using the orientation of the Earth, those two position measurements, and the distance between the two locations on the Earth, the distance to the Moon can be triangulated:
Calculuses
[edit | edit source]Calculus uses methods originally based on the summation of infinitesimal differences.
It includes the examination of changes in an expression by smaller and smaller differences.
Derivatives
[edit | edit source]Def. a result of an operation of deducing one function from another according to some fixed law is called a derivative.
Let
be a function where values of may be any real number and values resulting in are also any real number.
- is a small finite difference in which when put into the function produces a .
These small differences can be manipulated with the operations of arithmetic: addition (), subtraction (), multiplication (), and division ().
Dividing by and taking the limit as → 0, produces the slope of a line tangent to f(x) at the point x.
For example,
as and go towards zero,
This ratio is called the derivative.
Partial derivatives
[edit | edit source]Let
then
where z is held constant and
where x is held constant.
Gradients
[edit | edit source]Notation: let the symbol be the gradient, i.e., derivatives for multivariable functions.
Area under a curve
[edit | edit source]Consider the curve in the graph in the section about areas. The x-direction is left and right, the y-direction is vertical.
For
the area under the curve shown in the diagram at right is the light purple rectangle plus the dark purple rectangle in the top figure
Any particular individual rectangle for a sum of rectangular areas is
The approximate area under the curve is the sum of all the individual (i) areas from i = 0 to as many as the area needed (n):
Integrals
[edit | edit source]Def. a number, the limit of the sums computed in a process in which the domain of a function is divided into small subsets and a possibly nominal value of the function on each subset is multiplied by the measure of that subset, all these products then being summed is called an integral.
Notation: let the symbol represent the integral.
This can be within a finite interval [a,b]
when i = 0 the integral is evaluated at and i = n the integral is evaluated at . Or, an indefinite integral (without notation on the integral symbol) as n goes to infinity and i = 0 is the integral evaluated at x = 0.
Theoretical calculus
[edit | edit source]Def. a branch of mathematics that deals with the finding and properties ... of infinitesimal differences [or changes] is called a calculus.
Calculus focuses on limits, functions, derivatives, integrals, and infinite series.
Although calculus (in the sense of analysis) is usually synonymous with infinitesimal calculus, not all historical formulations have relied on infinitesimals (infinitely small numbers that are nevertheless not zero).
Line integrals
[edit | edit source]Def. an integral the domain of whose integrand is a curve is called a line integral.
"The pulsar dispersion measures [(DM)] provide directly the value of
along the line of sight to the pulsar, while the interstellar Hα intensity (at high Galactic latitudes where optical extinction is minimal) is proportional to the emission measure"[33]
Vectors
[edit | edit source]
For standard basis, or unit, vectors (i, j, k) there may be vector components of a (ax, ay, az).
Def. a directed quantity, one with both magnitude and direction; the signed difference between two points is called a vector.
"An observed time series consists of N data values x(tα) taken at a set of N discrete times {tα}. Hence it defines an N-dimensional contravariant vector in sampling space, by taking as the αth component of the vector, the value of the data at time tα, i.e.,
This representation is the canonical basis for sampling space."[34]
Tensors
[edit | edit source]Def. a mathematical object consisting of a set of components with n indices each of which range from 1 to m where n is the rank and m is the dimension is called a tensor.
"An impressive array of time series analysis methods are equivalent to treating the data as a vector in function space, then projecting the data vector onto a subspace of low dimension. A geometric approach isolates and exposes many of the important features of time series techniques, directly adapts to irregular time spacing, and easily accommodates variable statistical weights. Tensor notation provides an ideal formalism for these techniques. It is quite convenient for distinguishing a variety of different vector spaces, and is the most compact notation for all the sums which arise in the analysis."[34]
"[T]he generally invariant line element
[contains] the spacetime metric tensor [which] plays a dual role: on the one hand it determines the spacetime geometry, on the other it represents the (ten components of the) gravitational potential, and is thus a dynamical variable."[35]
Electronic computers
[edit | edit source]Def. a programmable electronic device that performs mathematical calculations and logical operations, especially one that can process, store and retrieve large amounts of data very quickly; now especially, a small one for personal or home use employed for manipulating text or graphics, accessing the Internet, or playing games or media is called a computer.
A computer is a general purpose device that can be programmed to carry out a finite set of arithmetic or logical operations. Since a sequence of operations can be readily changed, the computer can solve more than one kind of problem.
Programmings
[edit | edit source]A computer program (also software, or just a program) is a sequence of instructions written to perform a specified task with a computer.[36] A computer requires programs to function, typically executing the program's instructions in a central processor.[37]
Computer programming (often shortened to programming or coding) is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs.
Probabilities
[edit | edit source]Def. a number, between 0 and 1, expressing the precise likelihood of an event happening is called a probability.
Probability is a measure of the expectation that an event will occur or a statement is true. Probabilities are given a value between 0 (will not occur) and 1 (will occur).[38] The higher the probability of an event, the more certain we are that the event will occur.
Statistics
[edit | edit source]Def. a mathematical science concerned with data collection, presentation, analysis, and interpretation is called statistics.
Statistics is the study of the collection, organization, analysis, interpretation, and presentation of data.[39][40] It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments.[39]
"Statistics of projections are derived under a number of different null hypotheses."[34]
Hypotheses
[edit | edit source]- Each mathematical approach requires a proof of concept.
See also
[edit | edit source]References
[edit | edit source]- ↑ 1.0 1.1 Philip B. Gove, ed (1963). Webster's Seventh New Collegiate Dictionary. Springfield, Massachusetts: G. & C. Merriam Company. pp. 1221.
- ↑ Evenson, KM (1972). "Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser". Physical Review Letters 29 (19): 1346–49. doi:10.1103/PhysRevLett.29.1346.
- ↑ Oxford English Dictionary, 2nd ed.: natural logarithm
- ↑ 4.0 4.1 4.2 Peale, S. J. (June 1974). "Possible histories of the obliquity of Mercury". Astronomical Journal 79 (6): 722-44. doi:10.1086/111604.
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 P. K. Seidelmann (1976). Measuring the Universe The IAU and astronomical units. International Astronomical Union. http://www.iau.org/public/measuring/. Retrieved 2011-11-27.
- ↑ International Astronomical Union "SI units" accessed February 18, 2010. (See Table 5 and section 5.15.) Reprinted from George A. Wilkins & IAU Commission 5, "The IAU Style Manual (1989)" (PDF file) in IAU Transactions Vol. XXB
- ↑ David R. Williams (September 2004). Sun Fact Sheet. Greenbelt, MD: NASA Goddard Space Flight Center. http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html. Retrieved 2011-12-20.
- ↑ Encyclopaedia Britannica, 1968, vol. 2, p. 645
- ↑ M Caspar, Kepler (1959, Abelard-Schuman), at pp.131–140; A Koyré, The Astronomical Revolution: Copernicus, Kepler, Borelli (1973, Methuen), pp. 277–279
- ↑ 10.0 10.1 Christopher M. Linton (2004). From Eudoxus to Einstein—A History of Mathematical Astronomy. Cambridge: Cambridge University Press. ISBN 978-0-521-82750-8.
- ↑ David R. Williams. Planetary Fact Sheet Notes. http://nssdc.gsfc.nasa.gov/planetary/factsheet/planetfact_notes.html.
- ↑ 12.0 12.1 J. D. Hays; John Imbrie; N. J. Shackleton (December 1976). "Variations in the Earth's Orbit: Pacemaker of the Ice Ages". Science 194 (4270). http://www.whoi.edu/science/GG/paleoseminar/ps/hays76.ps. Retrieved 2011-11-08.
- ↑ Frank H Shu (1982). The Physical Universe. University Science Books. p. 261. ISBN 0935702059. http://books.google.com/?id=v_6PbAfapSAC&pg=PA261.
- ↑ James Binney; Michael Merrifield (1998). Galactic Astronomy. Princeton University Press. p. 536. ISBN 0691025657. http://books.google.com/?id=arYYRoYjKacC&pg=PA536.
- ↑ Mark Reid (2008). "Mapping the Milky Way and the Local Group". In F. Combes, Keiichi Wada. Mapping the Galaxy and Nearby Galaxies. Springer. pp. 19–20. ISBN 0387727671. http://books.google.com/?id=bP9hZqoIfhMC&pg=PA19.
- ↑ Binney J.; Merrifield M.. "§10.6". op. cit.. ISBN 0691025657.
- ↑ E.E. Mamajek (2008). "On the distance to the Ophiuchus star-forming region". Astron. Nachr. AN 329: 12. doi:10.1002/asna.200710827.
- ↑ Steven R. Majewski (2008). "Precision Astrometry, Galactic Mergers, Halo Substructure and Local Dark Matter". Proceedings of IAU Symposium 248 3. doi:10.1017/S1743921308019790.
- ↑ Bryant, Jeff; Pavlyk, Oleksandr. "Kepler's Second Law", Wolfram Demonstrations Project. Retrieved December 27, 2009.
- ↑ James Schombert. Earth Coordinate System. University of Oregon Department of Physics. http://abyss.uoregon.edu/~js/ast121/lectures/lec03.html. Retrieved 19 March 2011.
- ↑ D. C. Gabuzda; J. F. C. Wardle; D. H. Roberts (January 15, 1989). "Superluminal motion in the BL Lacertae object OJ 287". The Astrophysical Journal 336 (1): L59-62. doi:10.1086/185361.
- ↑ R.W. Sinnott, "Virtues of the Haversine", Sky and Telescope, vol. 68, no. 2, 1984, p. 159
- ↑ Vincenty, Thaddeus (1975-04-01). "Direct and Inverse Solutions of Geodesics on the Ellipsoid with Application of Nested Equations" (PDF). Survey Review (Kingston Road, Tolworth, Surrey: Directorate of Overseas Surveys) 23 (176): 88–93. http://www.ngs.noaa.gov/PUBS_LIB/inverse.pdf. Retrieved 2008-07-21.
- ↑ Zeilik & Gregory 1998, p. 44.
- ↑ Benedict, G. Fritz et al. (1999). "Interferometric Astrometry of Proxima Centauri and Barnard's Star Using HUBBLE SPACE TELESCOPE Fine Guidance Sensor 3: Detection Limits for Substellar Companions". The Astronomical Journal 118 (2): 1086–1100. doi:10.1086/300975.
- ↑ Shorter Oxford English Dictionary. 1968. "Mutual inclination of two lines meeting in an angle"
- ↑ Oxford English Dictionary (Second ed.). 1989. http://dictionary.oed.com/cgi/entry/50171114?single=1&query_type=word&queryword=parallax&first=1&max_to_show=10.
- ↑ P. Kenneth Seidelmann (2005). Explanatory Supplement to the Astronomical Almanac. University Science Books. pp. 123–125. ISBN 1891389459.
- ↑ Cesare Barbieri (2007). Fundamentals of astronomy. CRC Press. pp. 132–135. ISBN 0750308869.
- ↑ 30.0 30.1 Astronomical Almanac e.g. for 1981, section D
- ↑ Astronomical Almanac, e.g. for 1981: see Glossary; for formulae see Explanatory Supplement to the Astronomical Almanac, 1992, p.400
- ↑ Gutzwiller, Martin C. (1998). "Moon-Earth-Sun: The oldest three-body problem". Reviews of Modern Physics 70 (2): 589. doi:10.1103/RevModPhys.70.589.
- ↑ R. J. Reynolds (May 1, 1991). "Line Integrals of ne and at High Galactic Latitude". The Astrophysical Journal 372 (05): L17-20. doi:10.1086/186013. http://adsabs.harvard.edu/full/1991ApJ...372L..17R. Retrieved 2013-12-17.
- ↑ 34.0 34.1 34.2 Grant Foster (January 1996). "Time Series Analysis by Projection. II. Tensor Methods for Time Series Analysis". The Astronomical Journal 111 (1): 555-65. http://adsabs.harvard.edu/full/1996AJ....111..555F. Retrieved 2013-12-16.
- ↑ Jiří Bičák (2000). "Selected Solutions of Einstein's Field Equations: Their Role in General Relativity and Astrophysics, In: Einstein’s Field Equations and Their Physical Implications". Lecture Notes in Physics (Berlin: Springer Berlin Heidelberg) 540: 1-126. doi:10.1007/3-540-46580-4_1. ISBN 978-3-540-67073-5. http://arxiv.org/pdf/gr-qc/0004016. Retrieved 2013-07-04.
- ↑ Stair, Ralph M. (2003). Principles of Information Systems, Sixth Edition. Thomson Learning, Inc.. pp. 132. ISBN 0-619-06489-7.
- ↑ Silberschatz, Abraham (1994). Operating System Concepts, Fourth Edition. Addison-Wesley. pp. 58. ISBN 0-201-50480-4.
- ↑ William Feller (1968). An Introduction to Probability Theory and its Applications. 1. ISBN 0-471-25708-7.
- ↑ 39.0 39.1 Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 0-19-920613-9
- ↑ The Free Online Dictionary
Further reading
[edit | edit source]- William Marshall Smart; Robin Michael Green (July 7, 1977). Textbook on Spherical Astronomy, Sixth Edition. Cambridge: University of Cambridge. pp. 431. ISBN 0 521 21516 1. http://books.google.com/books?id=W0f2vc2EePUC&lr=&source=gbs_navlinks_s. Retrieved 2012-05-18.
- Tenorio-Tagle G; Bodenheimer P (1988). "Large-scale expanding superstructures in galaxies". Annual Review of Astronomy and Astrophysics 26: 145–97. http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1988ARA%26A..26..145T.
External links
[edit | edit source]- Bing Advanced search
- Google Books
- Google scholar Advanced Scholar Search
- International Astronomical Union
- JSTOR
- Lycos search
- NASA/IPAC Extragalactic Database - NED
- NASA's National Space Science Data Center.
- Questia - The Online Library of Books and Journals
- SAGE journals online
- The SAO/NASA Astrophysics Data System
- Scirus for scientific information only advanced search
- SDSS Quick Look tool: SkyServer
- SIMBAD Astronomical Database
- Spacecraft Query at NASA
- SpringerLink
- Taylor & Francis Online
- Universal coordinate converter
- Wiley Online Library Advanced Search
- Yahoo Advanced Web Search
{{Principles of radiation astronomy}}{{Radiation astronomy resources}}




































































































![{\displaystyle \Delta x*\Delta y=[f(x+\Delta x)-f(x)]*\Delta x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c87941451bfff5016af8c18139a939d5f95302e2)










![{\displaystyle x^{\alpha }=[x({t_{1}}),x({t_{2}}),...,x({t_{N}})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1add046244106341cafc36c0974056652731c1d3)


