Distance to the Moon

Lunar nearside, major maria and craters are labeled. Credit: Peter Freiman, Cmglee, and background photograph by Gregory H. Revera.

This laboratory is an activity for you to determine a distance to the Moon.

Some suggested entities to consider are right ascension, declination, circular orbit, longitude, and latitude.

Evaluation Main resources: Judgments/Evaluations and Evaluations evaluation activity

Okay, this is an astronomy distance, or displacement, laboratory.

Yes, this laboratory is structured.

I will provide an example of calculations of the distance to the Moon. The rest is up to you.

Questions, if any, are best placed on the discussion page.

Control groups

For measuring a distance to the Moon, what would make an acceptable control group? Think about a control group to compare your experimental results and calculations to.

Sampling

This is a Landsat image of the Barringer Meteor Crater from space. Credit: National Map Seamless Server, NASA Earth Observatory.

Crater Copernicus is imaged on the Moon. Credit: NASA (image by Lunar Reconnaissance Orbiter).{{free media}}

One way to calculate an estimate for the distance to the Moon is to use a feature that occurs both on Earth and on the Moon. Subject to size and magnification, the distance should be a function of perceived size. The diameter of the Meteor Crater in the image is 35 mm. For an observer at the level of the crater, it is 1,186 m in diameter. The angle between the observer's path vertically decreases from 90° as the distance of the observer from the crater rim increases from 593 m for an observer starting level with the crater rim at the center.

Landsat 1 has a periapsis of 897 km and an apoapsis of 917 km, for an average of 907 km. If the Barringer Meteor Crater was photographed by Landsat 1, it produced a 35 mm diameter image at 907 km. This suggests a photographic "shrink factor". As the perceived size shrinks with distance from the crater, the "shrink factor" should remain constant until the camera onboard can no longer image the crater (spatial resolutions ranging from 15 to 60 meters). The tangent of the angle is 593 m / 907,000 m or about 6 x 10^-4.

For the Meteor Crater image:

$imagesize=1186m{\frac {593m}{907,000m\times 2}}=593m\times {\frac {593m}{distancem}}.$

For example, if the size of a crater in the image at the top of the page is 1 mm and the image was taken by the same Landsat 1 camera, then the distance to the crater is approximately 35 times the distance of Landsat 1 above the Meteor Crater or 35,000 km.

If there are 11 pixels/mm, then a comparable crater of one pixel diameter corresponds to a distance of 385,000 km, for a Moon at an average distance of 384,000 km.

"A lunar observation by Landsat could provide improved radiometric and geometric calibration of both the Thematic Mapper and the Multispectral Scanner in terms of absolute radiometry, determination of the modulation transfer function, and sensitivity to scattered light. A pitch of the spacecraft would be required."

Therefore, Landsat can take an image of the Moon. If its minimal image size corresponds to a crater comparable to the Meteor Crater, then such a Landsat image would yield a value for the distance to the Moon.

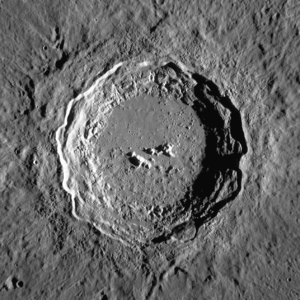
The crater Copernicus is 93 km in diameter or 78 times the size of the Meteor crater which would be about 78 pixels in the Landsat 1 image from Earth orbit (see the Copernicus crater in the Moon image at the top right) giving a distance of about 386,000 km.

Verification

File:Supermoon by Landsat 8.jpg

The supermoon is seen by Landsat 8. Credit: U.S. Geological Survey.{{fairuse}}

"The moon has an elliptical orbit that carries it between 363,000 and 406,000 kilometers from Earth. A so-called supermoon happens when a full moon coincides with the moon's closest approach to Earth. Original image data was obtained as dated on or about July 12, 2014."

Copernicus crater is upper left center.

Report

A distance to the Moon

by Marshallsumter

Abstract

Many methods can be used to calculate a distance to the Moon including using lunar parallax. Here a comparison of similar shaped craters is used with the Landsat system in orbit of Earth.

Introduction

Landsat 1 has imaged the Meteor crater. By calculating the tangent of the angle subtended by the satellite and assuming stable optics a calculation can be made using the Copernicus crater on the Moon.

Experiment

The size of the Meteor Crater was measured on the Earth. The size of the Copernicus crater was measured by the Lunar Reconnaissance Orbiter. A shrink factor calculation was made using the radius of the Meteor crater and an average distance of Landsat 1 from the rocky surface of Earth. To calculate an estimated distance to the Moon at Copernicus crater, a likely pixel density was matched to the ratio of sizes.

Results

A distance estimate of about 386,000 km was obtained.

Discussion

Exact parameters for the Landsat 8 calibration using a recent super Moon were not obtained. An estimated pixel diameter of 78 corresponded to the size ratio and appears close. Quality of optics of the Landsat series was assumed constant.

Conclusion

A reasonable distance to the Moon can be obtained by comparing similar Earth and Moon features.

Evaluation

To assess your calculations, including your justification, analysis and discussion, I will provide such an assessment of my example for comparison.

Evaluation

Exact photometric parameters such as focal length, magnification, and resolution were not used that could have better explained the approach. Shrink factor with distance is an unfamiliar term.

Hypotheses

Main resource: Hypotheses

1. The width of a feature decreases perceptively the further away vertically the observer travels.

External links

• African Journals Online
• Bing Advanced search
• Google Books
• Google scholar Advanced Scholar Search
• International Astronomical Union
• JSTOR
• Lycos search
• NASA's National Space Science Data Center
• Office of Scientific & Technical Information
• Questia - The Online Library of Books and Journals
• SAGE journals online
• The SAO/NASA Astrophysics Data System
• Scirus for scientific information only advanced search
• SpringerLink
• Taylor & Francis Online
• Universal coordinate converter
• Wiley Online Library Advanced Search
• Yahoo Advanced Web Search

{{History of science resources}}{{Reasoning resources}}