Skewness

From Wikiversity

Skewness refers to asymmetry (or "tapering") in the distribution of sample data:

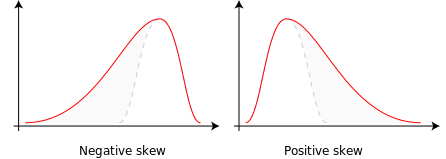
1. negative skew: The left tail is longer; the mass of the distribution is concentrated on the right of the figure. It has a few relatively low values. The distribution is said to be left-skewed. In such a distribution, the mean is lower than median which in turn is lower than the mode (i.e.; mean < median < mode); in which case the skewness is lower than zero.
2. positive skew: The right tail is longer; the mass of the distribution is concentrated on the left of the figure. It has a few relatively high values. The distribution is said to be right-skewed. In such a distribution, the mean is greater than median which in turn is greater than the mode (i.e.; mean > median > mode); in which case the skewness is greater than zero.

In a skewed (unbalanced, lopsided) distribution, the mean is farther out in the long tail than is the median. If there is no skewness or the distribution is symmetric like the bell-shaped normal curve then the mean = median = mode.

[edit] See also

• Kurtosis
• Statistics
• Research