Superconductivity
"Superconductivity is the complete disappearance of electrical resistance in certain materials, which occurs when they are cooled below a characteristic transition temperature, TC."[1]
Theoretical superconductivity
[edit | edit source]Def. the "property of a material whereby it has no resistance to the flow of an electric current"[2] is called superconductivity.
Def. "a pair of electrons, of opposite spin, that are thought to be the basis of superconductivity according to BCS theory"[3] are called a Cooper pair.
Materials
[edit | edit source]Def. matter "which may be shaped or manipulated, particularly in making something"[4] is called a material.
Properties
[edit | edit source]Def. an "[attribute or][5] abstract quality associated with an [individual][6], object or [concept][6]"[7] or "attribute or abstract quality which is characteristic of a class of objects"[6] is called a property.
Electrical resistances
[edit | edit source]Def. the "opposition offered by an electrical conductor to the flow of a current through itself,[8] resulting in a conversion of electrical energy into heat and radiation"[9] is called an electrical resistance.
Def. a "material constant denoting propensity for electrical resistance"[10] is called a resistivity.
Four-point probes
[edit | edit source]

The 4-point method can be used to measure the resistivity of a thin layer. It is necessary to place the 4 points away from the edges of the layer to be characterized, and to align them. See the diagram on the right. The current is sent by a current generator between the points 1 and 4, while the voltage is measured between the points 2 and 3. The ratio of the measured voltage to the current that passes through the sample gives the resistance of the section between probes 2 and 3.
Four-point probes are used to measure sheet resistance of thin films (particularly semiconductor thin films).[11]
The four-terminal technique is recommended for accurate measurement of resistance below 100 ohms.[12]
Electric currents
[edit | edit source]Def. "a net unidirectional movement of electrons, [or other charge carriers],[13] caused by a potential difference"[14] or "the net charge that passes through some cross-section of a conducting material (in one direction), divided by the time elapsed"[14] is called an electric current, or electrical current.
Superconducting materials
[edit | edit source]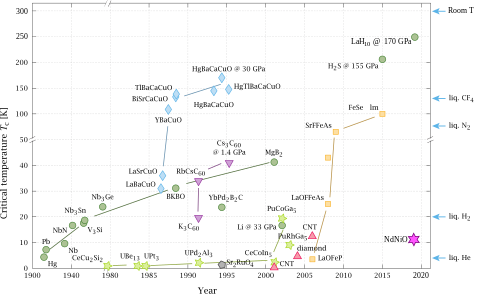
Colors represent different classes of materials:
"In a hydrogen-packed compound squeezed to ultra-high pressures, scientists have observed electrical current with zero resistance tantalizingly close to room temperature."[15]
"[L]anthanum hydride (or LaH
10, made up of one lanthanum atom and 10 hydrogen atoms), when under extreme pressure, is superconducting at temperatures as “warm” as -10 degrees Fahrenheit (-23 degrees Celsius)."[15]
In "2015, [...] a superconducting hydride (hydrogen sulfide, also called sulfur hydride or H
3S) [was first discovered]."[15]
"In superconductivity, electrons travel with perfect efficiency: Unlike in normal metals such as copper, there is no loss of energy through heat when the electrons move."[15]
"[L]anthanum hydride was coaxed to near-room-temperature superconductivity at 170 gigapascals (upwards of 24 million pounds per square inch), a pressure far higher than at the bottom of the ocean. Although such un-Earth-like conditions can only be fabricated using special equipment in a laboratory, the experiments suggest that room-temperature superconductivity could one day be possible under normal atmospheric pressure."[16]
"There's nothing in nature that prevents you from bringing superconductivity to room temperature. That's the conceptual relevance here."[16]
"To create the incredibly high pressures needed to form lanthanum hydride, they had to put very small amounts of the raw materials between two miniscule diamonds inside a tiny device called a diamond anvil cell. Then, with the turn of a wee screw, they upped the pressure."[17]
The "BCS theory accounted for lanthanum hydride’s superconducting state with two types of measurements. At the National MagLab, they put the compound inside a magnet and subjected it to magnetic fields, which, like other extreme environments such as very low or high temperatures, can affect a material’s properties. The way in which the lanthanum hydride's superconductivity varied as a function of magnetic field strength indicated that it is a conventional superconductor. In addition, at Max Planck, the compound passed the so-called isotope test. In that experiment, scientists substituted the hydrogen in one sample with deuterium, an isotope of hydrogen with a slightly different atomic mass. The temperature at which this modified compound stopped being superconducting (called the critical temperature) was different from that in the original compound."[17]
"If you see that critical temperature changes — usually it decreases — then this is a signature that it is conventional superconductivity."[18]
Meissner effect
[edit | edit source]
Def. "the total expulsion of magnetic flux from the interior of a superconducting metal when it is cooled in a magnetic field below a critical temperature, near absolute zero, at which the transition to superconductivity takes place"[19] is called the Meissner effect.
All "superconductors, whether 'conventional' or 'unconventional', exhibit the Meissner effect."[20]
There "is a single mechanism of superconductivity for all materials, that explains the Meissner effect and differs from the conventional mechanism in several fundamental aspects: it says that superconductivity is driven by lowering of kinetic rather than potential energy of the charge carriers, it requires conduction by holes rather than electrons in the normal state, and it predicts a non-homogeneous rigid charge distribution and an electric field in the interior of superconductors."[20]
The "Meissner effect can only be explained if: (i) superconductivity is driven by lowering of the kinetic energy of the charge carriers[6], and (ii) superconductors expel negative charge from the interior to the surface in the transition to superconductivity[7]. This physics results in a macroscopically inhomogeneous charge distribution[8] and in the existence of macroscopic zero-point motion which manifests itself in the form of a spin current[9] in the ground state of superconductors."[20]
"The points (i) and (ii) are intimately connected. Kinetic energy lowering means, e.g. via Heisenberg’s uncertaintly principle, expansion of the electronic wave function which in turn implies outward motion of negative charge. That outward motion of negative charge explains the generation of the Meissner current is immediately seen from the action of the Lorentz force[10]. That the Meissner effect is impossible in the absence of outward motion of charge is immediately seen from the equations of motion[11] and from the fact that there is no other source of electromotive force[12]. That kinetic energy lowering drives superconductivity follows from the fact that the Meissner effect cannot occur unless there is outward motion of negative charge; outward motion of negative charge implies charge separation, hence increase in potential energy, so the 'emf' driving it[12] has to be lowering of kinetic energy."[20]
The "close relationship that is known to exist between superconductors and superfluids, e.g. 4
He[13]. Both are macroscopic quantum phenomena[13]. Both exhibit frictionless flow with vanishing generalized vorticity. Kinetic energy lowering drives the superfluid transition in 4
He[14], so it is natural to conclude that it also drives the superconducting transition in superconductors."[20]
From "the preface of London’s book on superfluids, Vol. II[13]: “That something strange happens to liquid helium at about 2.2°K was noticed by Kammerlingh Onnes as early as 1911. He found that when the liquid is cooled below that temperature it starts expanding instead of continuing to contract, thus deviating from the behavior of most substances”. Indeed, the expansion of 4
He below the critical temperature is clear indication that the transition is driven by kinetic energy lowering, and it parallels[14] the wavefunction expansion and charge expulsion that [...] exists in superconductors, also driven by kinetic energy lowering."[20]
In "the preface of London’s book on superconductivity[13], [...] he writes: “It is not necessarily a configuration close to the minimum of the potential energy (lattice order) which is the most advantageous one for the energy balance, since by virtue of the uncertainty relation the kinetic energy also comes into play. If the resultant forces are sufficiently weak and act between sufficiently light particles, then the structure possessing the smallest total energy would be characterized by a good economy of the kinetic energy”."[20]
"Since the early days of the theory of hole superconductivity [...] it was clear that electron-hole asymmetry was intimately related to kinetic energy: the pairing interaction (correlated hopping) was termed ∆t[16], indicating its relation with the hopping amplitude t and kinetic energy (in contrast to other works[17–19]). The relation between kinetic energy lowering, wavefunction expansion and charge asymmetry became clearer when it was realized that superconductors expel negative charge from their interior to the surface[7, 8]. Experimentally, evidence for kinetic energy lowering was found in optical properties of cuprates and pnictides[20] as predicted theoretically several years before the experiments[21]."[20]
Electromotive forces
[edit | edit source]Def. "[potential][21] energy (not force) per unit electric charge [divided by electric charge][21] in a circuit; measured in volts"[22] is called an electromotive force.
An electromotive force, abbreviated emf (denoted and measured in volts),[23] is the electrical action produced by a non-electrical source.[24] A device that converts other forms of energy into electrical energy (a "transducer"),[25] such as a battery (converting chemical energy) or electric generator (converting mechanical energy),[24] provides an emf as its output.[25] Sometimes an analogy to water "pressure" is used to describe electromotive force.[26]
In electromagnetic induction, emf can be defined around a closed loop of electrical conductor as the electromagnetic work that would be done on an electric charge (an electron in this instance) if it travels once around the loop.[27] For a time-varying magnetic flux linking a loop, the electric potential scalar field is not defined due to a circulating electric vector field, but an emf nevertheless does work that can be measured as a virtual electric potential around the loop.[28]
Devices that can provide emf include electrochemical cells, thermoelectric devices, solar cells, photodiodes, electrical generators, electrical transformers and even Van de Graaff generators.[28][29]
In the case of a battery, the charge separation that gives rise to a voltage difference between the terminals is accomplished by chemical reactions at the electrodes that convert chemical potential energy into electromagnetic potential energy.[30][31] A voltaic cell can be thought of as having a "charge pump" of atomic dimensions at each electrode, that is:[32]
"A source of emf can be thought of as a kind of charge pump that acts to move positive charge from a point of low potential through its interior to a point of high potential. … By chemical, mechanical or other means, the source of emf performs work dW on that charge to move it to the high potential terminal. The emf ℰ of the source is defined as the work dW done per charge dq: ℰ = dW/dq."[32]
Inside a source of emf that is open-circuited, the conservative electrostatic field created by separation of charge exactly cancels the forces producing the emf. Thus, the emf has the same value but opposite sign as the integral of the electric field aligned with an internal path between two terminals A and B of a source of emf in open-circuit condition (the path is taken from the negative terminal to the positive terminal to yield a positive emf, indicating work done on the electrons moving in the circuit).[33]
Mathematically:
where Ecs is the conservative electrostatic field created by the charge separation associated with the emf, dℓ is an element of the path from terminal A to terminal B, and ‘·’ denotes the vector dot product.
Only the electric field that results from charge separation caused by the emf is counted. While a solar cell has an electric field that results from a contact potential (see contact potentials and solar cells), this electric field component is not included in the integral. Only the electric field that results from charge separation caused by photon energy is included.
This equation applies only to locations A and B that are terminals, and does not apply to paths between points A and B with portions outside the source of emf. This equation involves the electrostatic electric field due to charge separation Ecs and does not involve (for example) any non-conservative component of electric field due to Faraday's law of induction.
In the case of a closed path in the presence of a varying magnetic field, the integral of the electric field around a closed loop may be nonzero; one common application of the concept of emf, known as "induced emf" is the voltage induced in such a loop.[34] The "induced emf" around a stationary closed path C is:
where E is the entire electric field, conservative and non-conservative, and the integral is around an arbitrary but stationary closed curve C through which there is a varying magnetic field. The electrostatic field does not contribute to the net emf around a circuit because the electrostatic portion of the electric field is conservative (i.e., the work done against the field around a closed path is zero, see Kirchhoff's voltage law, which is valid, as long as the circuit elements remain at rest and radiation is ignored[35]).
This definition can be extended to arbitrary sources of emf and moving paths C:[36]
which is a conceptual equation mainly, because the determination of the "effective forces" is difficult.
Electrochemical thermodynamics
[edit | edit source]When multiplied by an amount of charge dQ the emf ℰ yields a thermodynamic work term ℰdQ that is used in the formalism for the change in Gibbs free energy when charge is passed in a battery:
where G is the Gibb's free energy, S is the entropy, V is the system volume, P is its pressure and T is its absolute temperature.
The combination ( ℰ, Q ) is an example of a conjugate pair of variables. At constant pressure the above relationship produces a Maxwell relation that links the change in open cell voltage with temperature T (a measurable quantity) to the change in entropy S when charge is passed isothermally and isobarically. The latter is closely related to the reaction entropy of the electrochemical reaction that lends the battery its power. This Maxwell relation is:[37]
If a mole of ions goes into solution (for example, in a Daniell cell, as discussed below) the charge through the external circuit is:
where n0 is the number of electrons/ion, and F0 is the Faraday constant and the minus sign indicates discharge of the cell. Assuming constant pressure and volume, the thermodynamic properties of the cell are related strictly to the behavior of its emf by:[37]
where ΔH is the standard enthalpy of reaction. The quantities on the right are all directly measurable.
Electrical voltage differences
[edit | edit source]An electrical voltage difference is sometimes called an emf.[38][39][40][41][42] The points below illustrate the more formal usage, in terms of the distinction between emf and the voltage it generates:
- For a circuit as a whole, such as one containing a resistor in series with a voltaic cell, electrical voltage does not contribute to the overall emf, because the voltage difference on going around a circuit is zero. (The ohmic IR voltage drop plus the applied electrical voltage sum to zero. See Kirchhoff's voltage law). The emf is due solely to the chemistry in the battery that causes charge separation, which in turn creates an electrical voltage that drives the current.
- For a circuit consisting of an electrical generator that drives current through a resistor, the emf is due solely to a time-varying magnetic field within the generator that generates an electrical voltage that in turn drives the current. (The ohmic IR drop plus the applied electrical voltage again is zero. See Kirchhoff's Law)
- A transformer coupling two circuits may be considered a source of emf for one of the circuits, just as if it were caused by an electrical generator; this example illustrates the origin of the term "transformer emf".
- A photodiode or solar cell may be considered as a source of emf, similar to a battery, resulting in an electrical voltage generated by charge separation driven by light rather than chemical reaction.[43]
- Other devices that produce emf are fuel cells, thermocouples, and thermopiles.[44]
In the case of an open circuit, the electric charge that has been separated by the mechanism generating the emf creates an electric field opposing the separation mechanism. For example, the chemical reaction in a voltaic cell stops when the opposing electric field at each electrode is strong enough to arrest the reactions. A larger opposing field can reverse the reactions in what are called reversible cells.[45][46]
The electric charge that has been separated creates an electric potential difference that can be measured with a voltmeter between the terminals of the device. The magnitude of the emf for the battery (or other source) is the value of this 'open circuit' voltage. When the battery is charging or discharging, the emf itself cannot be measured directly using the external voltage because some voltage is lost inside the source.[39]
It can, however, be inferred from a measurement of the current I and voltage difference V, provided that the internal resistance r already has been measured: ℰ = V + Ir.
Electrochemical cells
[edit | edit source]

The question of how batteries (galvanic cells) generate an emf occupied scientists for most of the 19th century. The "seat of the electromotive force" was eventually determined in 1889 by Walther Nernst[48] to be primarily at the interfaces between the electrodes and the electrolyte.[49]
Atoms in molecules or solids are held together by chemical bonding, which stabilizes the molecule or solid (i.e. reduces its energy). When molecules or solids of relatively high energy are brought together, a spontaneous chemical reaction can occur that rearranges the bonding and reduces the (free) energy of the system.[50] [51] In batteries, coupled half-reactions, often involving metals and their ions, occur in tandem, with a gain of electrons (termed "reduction") by one conductive electrode and loss of electrons (termed "oxidation") by another (reduction-oxidation or redox reactions). The spontaneous overall reaction can only occur if electrons move through an external wire between the electrodes. The electrical energy given off is the free energy lost by the chemical reaction system.[50]
As an example, a Daniell cell consists of a zinc anode (an electron collector) that is oxidized as it dissolves into a zinc sulfate solution. The dissolving zinc leaving behind its electrons in the electrode according to the oxidation reaction (s = solid electrode; aq = aqueous solution):
The zinc sulfate is the electrolyte in that half cell. It is a solution which contains zinc cations , and sulfate anions with charges that balance to zero.
In the other half cell, the copper cations in a copper sulfate electrolyte move to the copper cathode to which they attach themselves as they adopt electrons from the copper electrode by the reduction reaction:
which leaves a deficit of electrons on the copper cathode. The difference of excess electrons on the anode and deficit of electrons on the cathode creates an electrical potential between the two electrodes. (A detailed discussion of the microscopic process of electron transfer between an electrode and the ions in an electrolyte may be found in Conway.)[52] The electrical energy released by this reaction (213 kJ per 65.4 g of zinc) can be attributed mostly due to the 207 kJ weaker bonding (smaller magnitude of the cohesive energy) of zinc, which has filled 3d- and 4s-orbitals, compared to copper, which has an unfilled orbital available for bonding.[50]
If the cathode and anode are connected by an external conductor, electrons pass through that external circuit (light bulb in figure), while ions pass through the salt bridge to maintain charge balance until the anode and cathode reach electrical equilibrium of zero volts as chemical equilibrium is reached in the cell. In the process the zinc anode is dissolved while the copper electrode is plated with copper.[53] The so-called "salt bridge" has to close the electrical circuit while preventing the copper ions from moving to the zinc electrode and being reduced there without generating an external current. It is not made of salt but of material able to wick cations and anions (a dissociated salt) into the solutions. The flow of positively charged cations along the "bridge" is equivalent to the same number of negative charges flowing in the opposite direction.
If the light bulb is removed (open circuit) the emf between the electrodes is opposed by the electric field due to the charge separation, and the reactions stop.
For this particular cell chemistry, at 298 K (room temperature), the emf ℰ = 1.0934 V, with a temperature coefficient of dℰ/dT = −4.53×10−4 V/K.[37]
Voltaic cells
[edit | edit source]Volta developed the voltaic cell about 1792, and presented his work March 20, 1800.[54] Volta correctly identified the role of dissimilar electrodes in producing the voltage, but incorrectly dismissed any role for the electrolyte.[55] Volta ordered the metals in a 'tension series', “that is to say in an order such that any one in the list becomes positive when in contact with any one that succeeds, but negative by contact with any one that precedes it.”[56] A typical symbolic convention in a schematic of this circuit ( –||– ) would have a long electrode 1 and a short electrode 2, to indicate that electrode 1 dominates. Volta's law about opposing electrode emfs implies that, given ten electrodes (for example, zinc and nine other materials), 45 unique combinations of voltaic cells (10 × 9/2) can be created.
The electromotive force produced by primary (single-use) and secondary (rechargeable) cells is usually of the order of a few volts. The figures quoted below are nominal, because emf varies according to the size of the load and the state of exhaustion of the cell.
| EMF | Cell chemistry | Common name | ||
|---|---|---|---|---|
| Anode | Solvent, electrolyte | Cathode | ||
| 1.2 V | Cadmium | Water, potassium hydroxide | NiO(OH) | nickel–cadmium battery |
| 1.2 V | Mischmetal (hydrogen absorbing) | Water, potassium hydroxide | Nickel | nickel–metal hydride battery |
| 1.5 V | Zinc | Water, ammonium or zinc chloride | Carbon, manganese dioxide | zinc-carbon battery |
| 2.1 V | Lead | Water, sulfuric acid | Lead dioxide | Lead–acid battery |
| 3.6 V to 3.7 V | Graphite | Organic solvent, Li salts | LiCoO2 | lithium-ion battery |
| 1.35 V | Zinc | Water, sodium or potassium hydroxide | HgO | Mercury cell |
Contact potentials
[edit | edit source]When solids of two different materials are in contact, thermodynamic equilibrium requires that one of the solids assume a higher electrical potential than the other. This is called the contact potential.[57] Dissimilar metals in contact produce what is known also as a contact electromotive force or Galvani potential. The magnitude of this potential difference is often expressed as a difference in Fermi levels in the two solids when they are at charge neutrality, where the Fermi level (a name for the chemical potential of an electron system[58][59]) describes the energy necessary to remove an electron from the body to some common point (such as ground).[60] If there is an energy advantage in taking an electron from one body to the other, such a transfer will occur. The transfer causes a charge separation, with one body gaining electrons and the other losing electrons. This charge transfer causes a potential difference between the bodies, which partly cancels the potential originating from the contact, and eventually equilibrium is reached. At thermodynamic equilibrium, the Fermi levels are equal (the electron removal energy is identical) and there is now a built-in electrostatic potential between the bodies.
The original difference in Fermi levels, before contact, is referred to as the emf.[61] The contact potential cannot drive steady current through a load attached to its terminals because that current would involve a charge transfer. No mechanism exists to continue such transfer and, hence, maintain a current, once equilibrium is attained.
One might inquire why the contact potential does not appear in Kirchhoff's law of voltages as one contribution to the sum of potential drops. The customary answer is that any circuit involves not only a particular diode or junction, but also all the contact potentials due to wiring and so forth around the entire circuit. The sum of all the contact potentials is zero, and so they may be ignored in Kirchhoff's law.[62][63]
Meissner effects
[edit | edit source]"An electromotive force is a non-electric force that moves electric charges against the direction dictated by electric fields. In a voltaic cell, an electromotive force moves positive charges from the negative to the positive electrode (raising their electric potential energy). Similarly in the Meissner effect an electromotive force is needed to accelerate the electric charges near the surface carrying the developing Meissner current in direction opposite to that dictated by the electric force generated by Faraday’s law as the magnetic field lines are moving out[22]."[20]
"A quantum particle confined to a finite volume exerts “quantum pressure” against the confining walls. This quantum pressure, times the area over which it acts, gives us a force. [This] is the electromotive force that explains both the physics of voltaic cells and the Meissner effect."[20]
In the diagram on the right, the essence of superconductivity is described as an "electron in an expanding orbit with fixed angular momentum [L] lowers its kinetic energy (Ks < Kn), increases its diamagnetic susceptibility and causes expulsion of negative charge. The top orbit represents the normal state, with , the bottom one the superconducting state, with rs = ."[20]
See also
[edit | edit source]References
[edit | edit source]- ↑ AxelBoldt (13 October 2001). "Superconductivity". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ Moglex (2 November 2006). "superconductivity". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ SemperBlotto (16 March 2006). "Cooper pair". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ Dmh (6 September 2004). "material". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ DCDuring (19 November 2007). "property". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ 6.0 6.1 6.2 Verbo (13 March 2009). "property". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ Dmh (10 September 2004). "property". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ Saltmarsh (15 December 2005). electrical resistance. San Francisco, California: Wikimedia Foundation, Inc. https://en.wiktionary.org/wiki/electrical_resistance. Retrieved 2014-02-13.
- ↑ Tohru (30 December 2006). electrical resistance. San Francisco, California: Wikimedia Foundation, Inc. https://en.wiktionary.org/wiki/electrical_resistance. Retrieved 2014-02-13.
- ↑ Gamren (8 April 2016). "resistivity". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ Chandra, H., et al. Open-Source Automated Mapping Four-Point Probe. Materials 2017, 10(2), 110. doi: 10.3390/ma10020110
- ↑ Manual for the Racal-Dana Databridge 9343M: "If the resistance value is low, less than 100 ohms, make a four-terminal connection..."
- ↑ Latrissium (19 November 2017). "electric current". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ 14.0 14.1 Gamren (10 April 2017). "electric current". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ 15.0 15.1 15.2 15.3 Mikhail Eremets (22 May 2019). ""Superhydride" shows superconductivity at record-warm temperature". Tallahassee, Florida USA: National High Magnetic Field Laboratory. Retrieved 23 May 2019.
- ↑ 16.0 16.1 Luis Balicas (22 May 2019). ""Superhydride" shows superconductivity at record-warm temperature". Tallahassee, Florida USA: National High Magnetic Field Laboratory. Retrieved 23 May 2019.
- ↑ 17.0 17.1 Kristen Coyne (22 May 2019). ""Superhydride" shows superconductivity at record-warm temperature". Tallahassee, Florida USA: National High Magnetic Field Laboratory. Retrieved 23 May 2019.
- ↑ Shirin Mozaffari (22 May 2019). ""Superhydride" shows superconductivity at record-warm temperature". Tallahassee, Florida USA: National High Magnetic Field Laboratory. Retrieved 23 May 2019.
- ↑ SemperBlotto (12 April 2006). "Meissner effect". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ 20.00 20.01 20.02 20.03 20.04 20.05 20.06 20.07 20.08 20.09 20.10 J. E. Hirsch (March 2012). "The origin of the Meissner effect in new and old superconductors". Physica Scripta 85 (3, article id. 035704): 11. doi:10.1088/0031-8949/85/03/035704. https://arxiv.org/pdf/1201.0139. Retrieved 23 May 2019.
- ↑ 21.0 21.1 Dormy Carla (3 July 2009). "electromotive force". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ SemperBlotto (13 August 2005). "electromotive force". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 23 May 2019.
{{cite web}}:|author=has generic name (help) - ↑ emf. (1992). American Heritage Dictionary of the English Language 3rd ed. Boston:Houghton Mifflin.
- ↑ 24.0 24.1 Stewart, Joseph V. (2001). Intermediate electromagnetic theory. World Scientific. p. 389.
- ↑ 25.0 25.1 Tipler, Paul A. (January 1976). Physics. New York, NY: Worth Publishers, Inc.. p. 803. ISBN 978-0-87901-041-6.
- ↑ Irving Langmuir (1916). "The Relation Between Contact Potentials and Electrochemical Action". Transactions of the American Electrochemical Society (The Society) 29: 175. https://books.google.com/books?id=OW0SAAAAYAAJ&pg=PA172.
- ↑ David M. Cook (2003). The Theory of the Electromagnetic Field. Courier Dover. p. 157. ISBN 978-0-486-42567-2. https://books.google.com/books?id=bI-ZmZWeyhkC&pg=PA157.
- ↑ 28.0 28.1 Lawrence M Lerner (1997). Physics for scientists and engineers. Jones & Bartlett Publishers. pp. 724–727. ISBN 978-0-7637-0460-5. https://books.google.com/books?id=Nv5GAyAdijoC&pg=PA727.
- ↑ Paul A. Tipler; Gene Mosca (2007). Physics for Scientists and Engineers (6 ed.). Macmillan. p. 850. ISBN 978-1-4292-0124-7. https://books.google.com/books?id=BMVR37-8Jh0C&pg=PA850.
- ↑ Alvin M. Halpern; Erich Erlbach (1998). Schaum's outline of theory and problems of beginning physics II. McGraw-Hill Professional. p. 138. ISBN 978-0-07-025707-8. https://books.google.com/books?id=vN2chIay624C&pg=PA138.
- ↑ Robert L. Lehrman (1998). Physics the easy way. Barron's Educational Series. p. 274. ISBN 978-0-7641-0236-3. https://books.google.com/books?id=wMhCxOsPNE8C&pg=PA274.
- ↑ 32.0 32.1 Singh, Kongbam Chandramani (2009). "§3.16 EMF of a source". Basic Physics. Prentice Hall India. p. 152. ISBN 978-81-203-3708-4. https://books.google.com/books?id=oS_vSI-3yuwC.
- ↑ David J Griffiths (1999). Introduction to Electrodynamics (3rd ed.). Pearson/Addison-Wesley. p. 293. ISBN 978-0-13-805326-0.
- ↑ Richard P. Olenick; Tom M. Apostol; David L. Goodstein (1986). Beyond the mechanical universe: from electricity to modern physics. Cambridge University Press. p. 245. ISBN 978-0-521-30430-6. https://books.google.com/books?id=Ht4T7C7AXZIC&pg=RA1-PA245&dq=define+electromotive-force+around-a-closed-path.
- ↑ McDonald, Kirk T. (2012). "Voltage Drop, Potential Difference and EMF" (PDF). Physics Examples. Princeton University. p. 1, fn. 3.
- ↑ David M. Cook (2003). The Theory of the Electromagnetic Field. Courier Dover. p. 158. ISBN 978-0-486-42567-2. https://books.google.com/books?id=bI-ZmZWeyhkC&pg=PA158.
- ↑ 37.0 37.1 37.2 Colin B P Finn (1992). Thermal Physics. CRC Press. p. 163. ISBN 978-0-7487-4379-7. https://books.google.com/books?id=BTMPThGxXQ0C&pg=PA162.
- ↑ M. Fogiel (2002). Basic Electricity. Research & Education Association. p. 76. ISBN 978-0-87891-420-3. https://books.google.com/books?id=_DapslzANfwC&pg=PA76.
- ↑ 39.0 39.1 David Halliday; Robert Resnick; Jearl Walker (2008). Fundamentals of Physics (6th ed.). Wiley. p. 638. ISBN 978-0-471-75801-3. https://books.google.com/books?id=VXlEQlznCO0C&pg=PA638.
- ↑ Roger L Freeman (2005). Fundamentals of Telecommunications (2nd ed.). Wiley. p. 576. ISBN 978-0-471-71045-5. https://books.google.com/books?id=6_yQ-dEGc5wC&pg=PA576.
- ↑ Terrell Croft (1917). Practical Electricity. McGraw-Hill. p. 533. https://books.google.com/books?id=zuZMAAAAMAAJ&pg=PA533.
- ↑ Leonard B Loeb (2007). Fundamentals of Electricity and Magnetism (Reprint of Wiley 1947 3rd ed.). Read Books. p. 86. ISBN 978-1-4067-0733-5. https://books.google.com/books?id=zw-3icfx9qAC&pg=PA86.
- ↑ Jenny Nelson (2003). The Physics of Solar Cells. Imperial College Press. p. 7. ISBN 978-1-86094-349-2. https://books.google.com/books?id=s5NN34HLWO8C&pg=PA6.
- ↑ John S. Rigden, (editor in chief), Macmillan encyclopedia of physics. New York : Macmillan, 1996.
- ↑ J. R. W. Warn; A. P. H. Peters (1996). Concise Chemical Thermodynamics (2 ed.). CRC Press. p. 123. ISBN 978-0-7487-4445-9. https://books.google.com/books?id=oCTRVcJ1mqYC&pg=PA123.
- ↑ Samuel Glasstone (2007). Thermodynamics for Chemists (Reprint of D. Van Nostrand Co (1964) ed.). Read Books. p. 301. ISBN 978-1-4067-7322-4. https://books.google.com/books?id=oW5XqmTSXyEC&pg=RA1-PA301.
- ↑ Nikolaus Risch (2002). "Molecules - bonds and reactions". In L Bergmann. Constituents of Matter: Atoms, Molecules, Nuclei, and Particles. CRC Press. ISBN 978-0-8493-1202-1. https://books.google.com/books?id=mGj1y1WYflMC&printsec=frontcover#PPA374,M1.
- ↑ Nernst, Walter (1889). "Die elektromotorische Wirksamkeit der Ionen". Z. Phys. Chem. 4: 129.
- ↑ Florian Cajori (1899). A History of Physics in Its Elementary Branches: Including the Evolution of Physical Laboratories. The Macmillan Company. pp. 218–219. https://books.google.com/books?id=ICASAAAAYAAJ&pg=PA219.
- ↑ 50.0 50.1 50.2 Schmidt-Rohr, K. (2018). "How Batteries Store and Release Energy: Explaining Basic Electrochemistry" ‘’J. Chem. Educ.’’ 95: 1801-1810. http://dx.doi.org/10.1021/acs.jchemed.8b00479
- ↑ The brave reader can find an extensive discussion for organic electrochemistry in Christian Amatore (2000). "Basic concepts". Organic electrochemistry (4 ed.). CRC Press. ISBN 978-0-8247-0430-8. https://books.google.com/books?id=tBxxZclgKyMC&pg=PA23.
- ↑ BE Conway (1999). "Energy factors in relation to electrode potential". Electrochemical supercapacitors. Springer. p. 37. ISBN 978-0-306-45736-4. https://books.google.com/books?id=8yvzlr9TqI0C&pg=PA37.
- ↑ R. J. D. Tilley (2004). Understanding Solids. Wiley. p. 267. ISBN 978-0-470-85275-0. https://books.google.com/books?id=ZVgOLCXNoMoC&pg=PA267.
- ↑ Paul Fleury Mottelay (2008). Bibliographical History of Electricity and Magnetism (Reprint of 1892 ed.). Read Books. p. 247. ISBN 978-1-4437-2844-7. https://books.google.com/books?id=9vzti90Q8i0C&pg=RA1-PA247.
- ↑ Helge Kragh (2000). "Confusion and Controversy: Nineteenth-century theories of the voltaic pile". Nuova Voltiana:Studies on Volta and His Times (Università degli studi di Pavia). Archived from the original on 2009-03-20. https://web.archive.org/web/20090320064922/http://ppp.unipv.it/Collana/Pages/Libri/Saggi/NuovaVoltiana_PDF/sei.pdf.
- ↑ Linnaus Cumming (2008). An Introduction to the Theory of Electricity (Reprint of 1885 ed.). BiblioBazaar. p. 118. ISBN 978-0-559-20742-6. https://books.google.com/books?id=Nrb8723u4WEC&pg=PA118.
- ↑ George L. Trigg (1995). Landmark experiments in twentieth century physics (Reprint of Crane, Russak & Co 1975 ed.). Courier Dover. p. 138 ff. ISBN 978-0-486-28526-9. https://books.google.com/books?id=YOQ9fi5yQ4sC&pg=PA138.
- ↑ Angus Rockett (2007). "Diffusion and drift of carriers". Materials science of semiconductors. New York, NY: Springer Science. p. 74 ff. ISBN 978-0-387-25653-5. https://books.google.com/books?id=n5zMiMfw6ZUC&pg=PA74.
- ↑ Charles Kittel (2004). "Chemical potential in external fields". Elementary Statistical Physics (Reprint of Wiley 1958 ed.). Courier Dover. p. 67. ISBN 978-0-486-43514-5. https://books.google.com/books?id=5sd9SAoRjgQC&pg=PA67.
- ↑ George W. Hanson (2007). Fundamentals of Nanoelectronics. Prentice Hall. p. 100. ISBN 978-0-13-195708-4. https://books.google.com/books?id=L7AUi7ltCksC&pg=PA100.
- ↑ Norio Sato (1998). "Semiconductor photoelectrodes". Electrochemistry at metal and semiconductor electrodes (2nd ed.). Elsevier. p. 110 ff. ISBN 978-0-444-82806-4. https://books.google.com/books?id=olQzaXNgM74C&pg=PA110.
- ↑ Richard S. Quimby (2006). Photonics and lasers. Wiley. p. 176. ISBN 978-0-471-71974-8. https://books.google.com/books?id=82f-gIvtC7wC&pg=PA176.
- ↑ Donald A. Neamen (2002). Semiconductor physics and devices (3rd ed.). McGraw-Hill Professional. p. 240. ISBN 978-0-07-232107-4. https://books.google.com/books?id=9oEifMuMAVsC&pg=PA240.
External links
[edit | edit source]- 4 wire resistance measurement tutorial video (HD)
- Four-Point Techniques for Measuring Electrical Conductivity and Resistivity
- Explanatory Video about Four Wire Resistance Measurement in Energy Systems using Kelvin Clamps




![{\displaystyle {\mathcal {E}}=\oint _{C}\left[{\boldsymbol {E}}+{\boldsymbol {v}}\times {\boldsymbol {B}}\right]\cdot \mathrm {d} {\boldsymbol {\ell }}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3a083633dbacbcd81038a0eddb7a886e690bfe9)











