Charges/Interactions/Weak
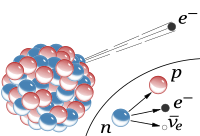
The weak interaction is expressed with respect to nuclear electrons and the continuous β-ray emission spectrum of β decay.[1]
Theoretical weak interactions
[edit | edit source]
"If Egrav is the gravitational energy of a star and Etherm is its total thermal energy, then the binding energy of the star is given by Ebind = Egrav + Etherm < 0, where Egrav is negative and Etherm is positive. The temperature of the cores of stars is determined by the balance between the gravitational attraction and the gas pressure. Since the gravitational energy determines the gravitational force and the thermal energy determines the gas pressure, it is obvious that there exists a relation between the two. If the gas in the star behaves like an ideal gas, then 2Etherm + Egrav = 0, a result which is known as the viral theorem.14 The theorem is extremely simple and can be derived in just 6 lines.15"[2]
"14Poincaré, H., Lecons sur les hypothéses cosmogoniques, Librarie Scientifique, A. Hermann, 1811. This theorem is also the basis for the negative effective specific heat of stars. Only at this point do we need the Clausius connection between kinetic energy and temperature [Clausius, R.J.E., Phil. Mag. 2, 1 (1851); ibid. 102; ibid. 12, 81 (1856)]. The temperature is given by the kinetic energy divided by the Boltzmann constant. If the star loses energy L, it must contract, i.e., reduce its radius, and consequently lower its negative gravitational energy Egrav. The kinetic energy T is then more positive, so the temperature rises. In this way the star can lose energy and increases its temperature, in contrast to normal matter. This is one of Eddington's famous paradoxes about stars: they lose energy and heat up."[2]
"15 See Jeans, Astronomy and Cosmogony, Cambridge University Press, 1929, p. 67."[2]
In the theoretical diagram on the right, the suggested quarks are shown as up (u), down (d), strange (s), charm (c), top (t) and bottom (b).
Electromagnetic interactions
[edit | edit source]Electromagnetic interactions act over a distance (r) by
Neutrons
[edit | edit source]"In 1937, Gamow and Teller36 postulated an extremely important addition to Fermi's β-decay theory. They realized that there are cases where the Fermi theory fails to explain the decays. Consequently, Gamow and Teller proposed an ad hoc solution to explain the discrepancy. [... simplifying] the difference between the Fermi and Gamow-Teller interactions as they are expressed in the reaction relevant to stars, namely p + p → 2D + e+ + ν. In a Fermi interaction which converts a proton into a neutron and vice versa, the sum of all spins of the particles does not change. In a Gamow-Teller interaction, the total spin must change by one unit."[2]
"What Gamow and Teller actually discovered was that the weak force, which is responsible for the β-decay, has two different components which behave and act differently and have different strengths. A good example is the electromagnetic force which can appear as a Coulomb force between electric charges or as a magnetic force acting on moving charges. The electric and magnetic components behave differently. Fierz37 generalized the theory by combining the Fermi and Gamow-Teller conditions into a unified theory of this complicated force."[2]
"37Fierz, M., Zeit. für Phys. 194, 553 (1937)."[2]
"When two particles are very close, the mutual screening [gives] rise to a short-range strong force which is of the right strength to hold protons and neutrons within the atomic nuclei. [...] The same process originates also a short-range "weak" force on the electron [of the simple deuterium nucleus] closely orbiting a proton, giving rise to the neutron structure which undergoes β- decay."[3]
Experimentally, for the β- decay of 60Co:
- subsequently
Protons
[edit | edit source]Part of the pp chain is
- where subsequently
Experimentally, for the β+ decay of 11C:
- subsequently
Also experimentally, for the β+ decay of 12Mg:
- subsequently
"Because parity symmetry (invariance under the spatial inversion (x, y, z) → (−x, −y, −z)) is violated only in the weak interaction, it provides a tool with which to isolate the weak interaction and thus to measure the proton’s weak charge1. Here we report the value 0.0719 ± 0.0045, where the uncertainty is one standard deviation, derived from our measured parity-violating asymmetry in the scattering of polarized electrons on protons, which is −226.5 ± 9.3 parts per billion (the uncertainty is one standard deviation)."[4]
Beta particles
[edit | edit source]"In radiation theory, the total number of light quanta is not constant. Light quanta are created when they are emitted from an atom, and are annihilated when they are absorbed."[1]
By analogy to radiation theory, "The total number of electrons [and neutrinos] is not necessarily constant. Electrons (or neutrinos) can be created or annihilated. This ... is not analogous to the creation or annihilation of an electron-positron pair."[1]
"[E]ach transition from a neutron to a proton is associated with the creation of an electron and a neutrino. The reverse process (change of a proton into a neutron) must be associated with the annihilation of an electron and a neutrino."[1]
"The Z boson may be studied as a resonance"[5]
The "observation of four electron-positron pairs and one muon pair [...] have the signature of a two-body decay of a particle of mass ~ 95 GeV/c2. These events fit well the hypothesis that they are produced by the process p¯ + p --> Z0 + X (with Z0 --> 1+ + 1-), where Z0 is the Intermediate Vector Boson postulated by the electroweak theories as the mediator of weak neutral currents."[6]
β decay
[edit | edit source]"A β decay is the process by which a nuclear neutron changes into a proton at the same time as an electron, which is observed as a β ray, and a neutrino are emitted"[1].
Electrons
[edit | edit source]Nuclear electrons apparently may be bound in orbits of nuclear dimensions.[1]
"[A] nucleus [may consist] only of heavy particles - protons and neutrons."[1]
Neutrinos
[edit | edit source]As part of the Mikheyev–Smirnov–Wolfenstein effect, "The presence of electrons in matter [affects neutrino propagation] due to charged current coherent forward scattering of the electron neutrinos (i.e., weak interaction). The coherent forward scattering is analogous to the electromagnetic process leading to the refractive index of light in a medium. ... With antineutrinos, the ... effective charge that the weak interaction couples to (called weak isospin) has an opposite sign."[7]
Opticals
[edit | edit source]"The observation of a neutrino burst within 3 h of the associated optical burst from supernova 1987A in the Large Magellanic Cloud provides a new test of the weak equivalence principle, by demonstrating that neutrinos and photons follow the same trajectories in the gravitational field of the galaxy."[8]
Intergalactic medium
[edit | edit source]The "decrease of the size of extended source with the increase of energy allows to measure weak magnetic fields with magnitudes in the range from ≤ 10−16 G to 10−12G if they exist in the voids of the Large Scale Structure."[9]
Physics
[edit | edit source]The weak interaction of the weak force acts over a distance (r) given by
Hypotheses
[edit | edit source]- As different charges begin to mix, the electromagnetic interaction becomes weaker.
See also
[edit | edit source]References
[edit | edit source]- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Fred L. Wilson (December 1968). "Fermi's Theory of Beta Decay". American Journal of Physics 36 (12): 1150-60. http://microboone-docdb.fnal.gov/cgi-bin/RetrieveFile?docid=953;filename=FermiBetaDecay1934.pdf;version=1. Retrieved 2012-06-24.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Giora Shaviv (2013). Giora Shaviv. ed. Towards the Bottom of the Nuclear Binding Energy, In: The Synthesis of the Elements. Berlin: Springer-Verlag. pp. 169-94. doi:10.1007/978-3-642-28385-7_5. ISBN 978-3-642-28384-0. http://link.springer.com/chapter/10.1007/978-3-642-28385-7_5#page-1. Retrieved 2013-12-19.
- ↑ Maurizio Michelini (October 2008). "The Common Physical Origin of the Gravitational, Strong and Weak Forces". Apeiron 15 (4): 440-64. http://www.rxiv.org/pdf/0810.0003v1.pdf. Retrieved 2013-11-07.
- ↑ The Jefferson Lab Qweak Collaboration (09 May 2018). "Precision measurement of the weak charge of the proton". Nature 557: 207–211. doi:10.1038/s41586-018-0096-0. https://www.nature.com/articles/s41586-018-0096-0. Retrieved 2018-5-10.
- ↑ Tord Riemann (December 1997). "Study of the Z Boson at LEP". arXiv. http://arxiv.org/pdf/hep-ph/9712435.pdf. Retrieved 2015-08-08.
- ↑ G. Arnison, A. Astbury, B. Aubert, C. Bacci, G. Bauer, A. Bézaguet, R. Böck, T. J. V. Bowcock, M. Calvetti, P. Catz, P. Cennini, S. Centro, F. Ceradini, S. Cittolin, D. Cline, C. Cochet, J. Colas, M. Corden, D. Dallman, D. Dau, M. Debeer, M. Della Negra, M. Demoulin, D. Denegri, A. di Ciaccio, D. Dibitonto, L. Dobrzynski, J. D. Dowell, K. Eggert, E. Eisenhandler, N. Ellis, P. Erhard, H. Faissner, M. Fincke, G. Fontaine, R. Frey, R. Frühwirth, J. Garvey, S. Geer, C. Ghesquière, P. Ghez, K. Giboni, W. R. Gibson, Y. Giraud-Héraud, A. Givernaud, A. Gonidec, G. Grayer, T. Hansl-Kozaecka, W. J. Haynes, L. O. Hertzberger, C. Hodges, D. Hoffmann, H. Hoffmann, D. J. Holthuizen, R. J. Homer, A. Honma, W. Jank, G. Jorat, P. I. P. Kalmus, V. Karimäki, R. Keeler, I. Kenyon, A. Kernan, R. Kinnunen, W. Kozanecki, D. Kryn, F. Lacava, J.-P. Laugier, J.-P. Lees, H. Lehmann, R. Leuchs, A. Lévêque, D. Linglin, E. Locci, J.-J. Malosse, T. Markiewicz, G. Maurin, T. McMahon, J.-P. Mendiburu, M.-N. Minard, M. Mohammadi, M. Moricca, K. Morgan, H. Muirhead, F. Muller, A. K. Nandi, L. Naumann, A. Norton, A. Orkin-Lecourtois, L. Paoluzi, F. Pauss, G. Piano Mortari, E. Pietarinen, M. Pimiä, A. Placci, J. P. Porte, E. Radermacher, J. Ransdell, H. Reithler, J.-P. Revol, J. Rich, M. Rijssenbeek, C. Roberts, J. Rohlf, P. Rossi, C. Rubbia, B. Sadoulet, G. Sajot, G. Salvi, G. Salvini, J. Sass, J. Saudraix, A. Savoy-Navarro, D. Schinzel, W. Scott, T. P. Shah, M. Spiro, J. Strauss, J. Streets, K. Sumorok, F. Szoncso, D. Smith, C. Tao, G. Thompson, J. Timmer, E. Tscheslog, J. Touminiemi, B. van Eijk, J.-P. Vialle, J. Vrana, V. Vuillemin, H. D. Wahl, P. Watkins, J. Wilson, C. Wulz, G. Y. Xie, M. Yvert, and E. Zurfluh (July 1983). "Experimental observation of lepton pairs of invariant mass around 95 GeV/c2 at the CERN SPS collider". Physics Letters B 126 (5): 398-410. doi:10.1016/0370-2693(83)90188-0. http://adsabs.harvard.edu/abs/1983PhLB..126..398A. Retrieved 2015-08-08.
- ↑ "Mikheyev–Smirnov–Wolfenstein effect, In: Wikipedia". San Francisco, California: Wikimedia Foundation, Inc. July 23, 2012. Retrieved 2012-08-23.
- ↑ Lawrence M. Krauss, Scott Tremaine (January 1988). "Test of the Weak Equivalence Principle for Neutrinos and Photons". Physical Review Letters 60 (3): 176–7. doi:10.1103/PhysRevLett.60.176. http://link.aps.org/doi/10.1103/PhysRevLett.60.176.
- ↑ A. Elyiv, A. Neronov, D.V. Semikoz (2009). "Gamma-ray induced cascades and magnetic fields in intergalactic medium". Physical Review D 80 (2): 11. doi:10.1103/PhysRevD.80.023010. http://prd.aps.org/abstract/PRD/v80/i2/e023010. Retrieved 2014-02-12.
- ↑ 70.109.186.143 (28 July 2011). Fundamental interaction. San Francisco, California: Wikimedia Foundation, Inc. http://en.wikipedia.org/wiki/Fundamental_interaction. Retrieved 2013-06-29.
Further reading
[edit | edit source]- Fred L. Wilson (December 1968). "Fermi's Theory of Beta Decay". American Journal of Physics 36 (12): 1150-60. http://microboone-docdb.fnal.gov/cgi-bin/RetrieveFile?docid=953;filename=FermiBetaDecay1934.pdf;version=1. Retrieved 2012-06-24.
External links
[edit | edit source]- Bing Advanced search
- Google Books
- Google scholar Advanced Scholar Search
- JSTOR
- Lycos search
- NASA's National Space Science Data Center
- NCBI All Databases Search
- Office of Scientific & Technical Information
- Questia - The Online Library of Books and Journals
- SAGE journals online
- The SAO/NASA Astrophysics Data System
- Scirus for scientific information only advanced search
- SpringerLink
- Taylor & Francis Online
- Wiley Online Library Advanced Search
- Yahoo Advanced Web Search
{{Radiation astronomy resources}}
{{Repellor vehicle}}









