Energy phantoms/Lecture

File:M87 jet Hubble.gif

The two images are a top panel of Hubble Space Telescope image showing the M87 jet streaming out from the galaxy's nucleus (bright round region at far left) and a bottom panel which contains a sequence of Hubble images showing motion of something at six times the speed of light. Credit: John Biretta/NASA/ESA/Space Telecsope Science Institute.

An energy phantom is an observational phenomenon that can be described in general terms of distances and times.

In the images at right are the effects of charged particles apparently moving six times the speed of light.

"We see almost a dozen clouds which appear to be moving out from the galaxy's center at between four and six times the speed of light. These are all located in a narrow [relativistic] jet of gas streaming out from the region of the black hole at the galaxy's center".

"We believe this apparent speed translates into an actual velocity just slightly below that of light itself."

"The speeds reported are two to three times faster than the fastest motions previously recorded in M87, the only nearby galaxy to show evidence for superluminal motion."

"This discovery goes a long way towards confirming that radio galaxies, quasars and exotic BL Lac objects are basically the same beast, powered by super massive black holes, and differ only in orientation with respect to the observer".

"Here we have, for the first time, a fairly normal radio galaxy with both excellent evidence for a super-massive black hole, as well as superluminal jet speeds similar to those seen in distant quasars and BL Lac objects."

"This is the first time superluminal motion has been seen with any optical telescope, and this discovery was made possible by the extremely fine resolution obtained by Hubble".

"The structure of relativistic jets in [active galactic nuclei] AGN on scales of light days reveals how energy propagates through jets, a process that is fundamental to galaxy evolution."

Positions

The SI derived "mechanical"
(that is, not electromagnetic or thermal)
units with kg, m and s

position	m
angular position/angle	unitless (radian)
velocity	m·s−1
angular velocity	s−1
acceleration	m·s−2
angular acceleration	s−2
jerk	m·s−3
"angular jerk"	s−3
specific energy	m2·s−2
absorbed dose rate	m2·s−3
moment of inertia	kg·m2
momentum	kg·m·s−1
angular momentum	kg·m2·s−1
force	kg·m·s−2
torque	kg·m2·s−2
energy	kg·m2·s−2
power	kg·m2·s−3
pressure and energy density	kg·m−1·s−2
surface tension	kg·s−2
spring constant	kg·s−2
irradiance and energy flux	kg·s−3
kinematic viscosity	m2·s−1
dynamic viscosity	kg·m−1·s−1
density (mass density)	kg·m−3
density (weight density)	kg·m−2·s−2
number density	m−3
action	kg·m2·s−1

In pre-Einstein relativity (known as Galilean relativity), time is considered an absolute, i.e., the time interval that is observed to elapse between any given pair of events is the same for all observers.

In addition to relying on absolute time, classical mechanics assumes Euclidean geometry for the structure of space.

Theoretical classical mechanics

Def. an "[amount of] intervening space between two points, usually geographical points, usually (but not necessarily) measured along a straight line" is called a distance.

Def. the "inevitable progression into the future with the passing of present events into the past" or the "inevitable passing of events from future to present then past" is called time.

Def. the "quantity of matter which a body contains, irrespective of its bulk or volume" or a "quantity of matter cohering together so as to make one body, or an aggregation of particles or things which collectively make one body or quantity" is called a mass.

Def. the "rate of motion or action, specifically the magnitude of the velocity; the rate distance is traversed in a given time" is called the speed.

Vectors

Main resources: Distances/Vectors and Vectors

The angular velocity of the particle at P with respect to the origin O is determined by the perpendicular component of the velocity vector v. Credit: Krishnavedala.

The angular velocity describes the speed of rotation and the orientation of the instantaneous axis about which the rotation occurs. The direction of the angular velocity pseudovector is along the axis of rotation; in this case (counter-clockwise rotation) the vector points up. Credit: dnet.

Def. the product of a body's mass and velocity is called momentum.

Def. the rotary inertia of a system [such as] an isolated rigid body is a measure of the extent to which an object will continue to rotate in the absence of an applied torque is called angular momentum.

Motions

The analysis of projectile motion is a part of classical mechanics. Credit: AntanO.

Essentially, motion boils down to where an object is, how fast it is going, and how fast it is changing how fast it is going.

In strict physical terms, these quantities are:

Position: the location of an object (generally from its centre of gravity) in relation to all other objects in a system.

Velocity: the rate at which the position changes.

Acceleration: The rate at which the object's velocity changes.

The units used to describe these quantities are:

• meter (m): the standard unit for distance in one direction. A meter is about 39 inches, or slightly more the three feet.
• second (s): the standard unit for time. a second is the time that elapses during 9,192,631,770 vibrations of the cesium 133 atom.

These relate to each other as follows:

Position = x (in meters)

Speeds and velocity

Velocity = change in position (distance d) divided by change in time (t)

$\mathbf {v} ={\mathrm {d} \mathbf {r} \over \mathrm {d} t}\,\!$.

The velocity of the first object as seen by the second object is

$\mathbf {u} '=\mathbf {u} -\mathbf {v} \,.$

Similarly, the first object sees the velocity of the second object as

$\mathbf {v'} =\mathbf {v} -\mathbf {u} \,.$

When both objects are moving in the same direction, this equation can be simplified to

$\mathbf {u} '=(u-v)\mathbf {d} \,.$

Or, by ignoring direction, the difference can be given in terms of speed only:

$u'=u-v\,.$

Angular momentum

This diagram describes the relationship between force (F), torque (τ), momentum (p), and angular momentum (L) vectors in a rotating system. 'r' is the radius. Credit: Yawe.

Angular momentum and energy are concepts developed to try to understand everyday reality.

An angular momentum L of a particle about an origin is given by

$\mathbf {L} =\mathbf {r} \times \mathbf {p}$

where r is the radius vector of the particle relative to the origin, p is the linear momentum of the particle, and × denotes the cross product (r · p sin θ). Theta is the angle between r and p.

Accelerations

Acceleration = change in velocity (v) divided by change in time

a = (change in v)/t

for example, if I were to walk in a straight line 10 m, and it took me 5 s to do this, my velocity would be:

v = (change in d)/t

v = 10 m/5 s

v = 2 m/s

my velocity was 2 m/s

In a similar fashion, if you knew my initial velocity to be 2 m/s and after a 20 s stretch, my velocity was 42 m/s, my acceleration would be

a = (change in v)/t

a = (42 m/s - 2 m/s)/20 s

a = (40 m/s)/20 s

a = 2 m/s²

my acceleration was 2 m/s²

Torques

Def. a rotational or twisting effect of a force is called a torque.

Def. a turning effect of a force applied to a rotational system at a distance from the axis of rotation is called a moment of force.

The moment is equal to the magnitude of the force multiplied by the perpendicular distance between its line of action and the axis of rotation.

A torque and a moment of force are the same. Each is a "unit of work done, or energy expended.

For an object with a fixed mass that is rotating about a fixed symmetry axis, the angular momentum is expressed as the product of the moment of inertia of the object and its angular velocity vector:

$\mathbf {L} =I{\boldsymbol {\omega }}$

where I is the moment of inertia of the object (in general, a tensor quantity), and ω is the angular velocity.

The moment of inertia is the mass property of a rigid body that defines the torque needed for a desired angular acceleration about an axis of rotation. Moment of inertia depends on the shape of the body and may be different around different axes of rotation. A larger moment of inertia around a given axis requires more torque to increase the rotation, or to stop the rotation, of a body about that axis. Moment of inertia depends on the amount and distribution of its mass, and can be found through the sum of moments of inertia of the masses making up the whole object, under the same conditions.

In two dimensions the angular velocity ω is given by

$\omega ={\frac {d\phi }{dt}}$

This is related to the cross-radial (tangential) velocity by:

$\mathrm {v} _{\perp }=r\,{\frac {d\phi }{dt}}$

An explicit formula for v_⊥ in terms of v and θ is:

$\mathrm {v} _{\perp }=|\mathrm {\mathbf {v} } |\,\sin(\theta )$

"Combining the above equations gives a formula for ω:

$\omega ={\frac {|\mathrm {\mathbf {v} } |\sin(\theta )}{|\mathrm {\mathbf {r} } |}}$

Energies

Main resources: Physics/Energies and Energies

Def. a "quantity that denotes the ability to do work and is measured in a unit dimensioned in mass × distance²/time² (ML²/T²) or the equivalent" is called energy.

Def. "[a] physical quantity that denotes ability to push, pull, twist or accelerate a body which is measured in a unit dimensioned in mass × distance/time² (ML/T²): SI: newton (N); CGS: dyne (dyn)" is called force.

In astronomy we estimate distances and times when and where possible to obtain forces and energy.

The key values to determine in both force and energy are (L/T²) and (L²/T²). Force (F) x distance (L) = energy (E), L/T² x L = L²/T². Force and energy are related to distance and time using proportionality constants.

Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them:
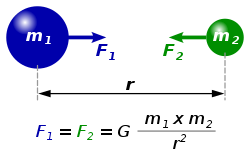
$F=G{\frac {m_{1}m_{2}}{r^{2}}}\$, where: F is the force between the masses, G is the gravitational constant, m1 is the first mass, m2 is the second mass, and r is the distance between the centers of the masses.	The diagram shows two masses attracting one another. Credit: .

In the International System of Units (SI) units, F is measured in newtons (N), m₁ and m₂ in kilograms (kg), r in meters (m), and the constant G is approximately equal to 6.674×10⁻¹¹
 N m² kg⁻².

Observationally, we may not know the origin of the force.

Coulomb's law states that the electrostatic force $F$ experienced by a charge, $q$ at position $r_{q}$, in the vicinity of another charge, $Q$ at position $r_{Q}$, in vacuum is equal to:

$F={qQ \over 4\pi \varepsilon _{0}}{1 \over {r^{2}}},$

where $\varepsilon _{0}$ is the electric constant and $r$ is the distance between the two charges.

Coulomb's constant is

$k_{e}=1/(4\pi \varepsilon _{0}\varepsilon ),$

where the constant $\varepsilon _{0}$ is called the permittivity of free space in SI units of C² m⁻² N⁻¹.

For reality, $\varepsilon$ is the relative (dimensionless) permittivity of the substance in which the charges may exist.

The energy $E$ for this system is

$E=F\cdot D,$

where $D$ is the displacement.

Unknown forces

Newton's second law of motion is that $F=ma$, where $F$ is the force applied, $m$ is the mass of the object receiving the force, and $a$ is the acceleration observed for the astronomical object. The newton is therefore:

${1~{\rm {N}}=1~{\rm {kg}}{\frac {\rm {m}}{{\rm {s}}^{2}}}}$

where:

N: newton

kg: kilogram

m: metre

s: second.

In dimensional analysis:

${\mathsf {F}}={\frac {\mathsf {ML}}{{\mathsf {T}}^{2}}}$

where

M: mass

L: length

T: time.

But, for a force of unknown type, mass or charge may be meaningless until proven applicable.

So that

${\mathsf {A}}={\mathsf {F/M}}={\frac {\mathsf {L}}{{\mathsf {T}}^{2}}},$

${\mathsf {A}}={\mathsf {F/Q}}={\frac {\mathsf {L}}{{\mathsf {T}}^{2}}},$

${\mathsf {P}}={\mathsf {E/M}}={\frac {{\mathsf {L}}^{2}}{{\mathsf {T}}^{2}}},$

and

${\mathsf {P}}={\mathsf {E/Q}}={\frac {{\mathsf {L}}^{2}}{{\mathsf {T}}^{2}}},$

where ${\mathsf {P}}$ may be called an energy phantom, or astronomical energy phantom.

Hypotheses

Main resource: Hypotheses

1. Positive and negative effective mass may be a representation of an electromagnetic type interaction that produces all four fundamental interactions.

See also

• Angular momentum and energy
• Column densities
• Energy phantoms, a problem set.
• Furlongs per fortnight
• Unknown coordinate systems
• Unusual units
• Vectors and coordinates

External links

{{Physics resources}}{{Radiation astronomy resources}}