Problems/Astronomy

Problems designed for astronomy help the student, the teacher, and the researcher to understand the astrophysics and astromathematics involved in astronomy.

Notations

Notation: let the symbol $R_{\oplus }$ indicate the Earth's radius.

Notation: let the symbol $R_{J}$ indicate the radius of Jupiter.

Notation: let the symbol $R_{\odot }$ indicate the solar radius.

Energy phantoms

This is an optical image in the visual range of Theta Ursae Majoris. It is listed in SIMBAD as an F7V spectral type star with a parallax of 74.19 mas. Credit: Aladin at SIMBAD.

Students start from specific situations of motion, determine how to calculate energy and convert units, then evaluate types of energy.

Energies

Def. a "quantity that denotes the ability to do work and is measured in a unit dimensioned in mass × distance²/time² (ML²/T²) or the equivalent"^[1] is called energy.

Def. a "physical quantity that denotes ability to push, pull, twist or accelerate a body which is measured in a unit dimensioned in mass × distance/time² (ML/T²): SI: newton (N); CGS: dyne (dyn)"^[2] is called force.

In astronomy we estimate distances and times when and where possible to obtain forces and energy.

The key values to determine in both force and energy are (L/T²) and (L²/T²). Force (F) x distance (L) = energy (E), L/T² x L = L²/T². Force and energy are related to distance and time using proportionality constants.

Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them:^[3]

F=G{\frac {m_{1}m_{2}}{r^{2}}}\

,

where:

F is the force between the masses,
G is the gravitational constant,
m₁ is the first mass,
m₂ is the second mass, and
r is the distance between the centers of the masses.

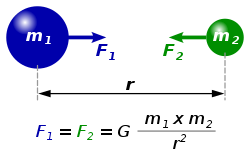
The diagram shows two masses attracting one another. Credit: .

In the International System of Units (SI) units, F is measured in newtons (N), m₁ and m₂ in kilograms (kg), r in meters (m), and the constant G is approximately equal to 6.674×10⁻¹¹
N m² kg⁻².^[4]

Observationally, we may not know the origin of the force.

Coulomb's law states that the electrostatic force $F$ experienced by a charge, $q$ at position $r_{q}$ , in the vicinity of another charge, $Q$ at position $r_{Q}$ , in vacuum is equal to:

F={qQ \over 4\pi \varepsilon _{0}}{1 \over {r^{2}}},

where $\varepsilon _{0}$ is the electric constant and $r$ is the distance between the two charges.

Coulomb's constant is

k_{e}=1/(4\pi \varepsilon _{0}\varepsilon ),

where the constant $\varepsilon _{0}$ is called the permittivity of free space in SI units of C² m⁻² N⁻¹.

For reality, $\varepsilon$ is the relative (dimensionless) permittivity of the substance in which the charges may exist.

The energy $E$ for this system is

E=F\cdot D,

where $D$ is the displacement.

Unknown forces

Newton's second law of motion is that $F=ma$ , where $F$ is the force applied, $m$ is the mass of the object receiving the force, and $a$ is the acceleration observed for the astronomical object. The newton is therefore:^[5]

{1~{\rm {N}}=1~{\rm {kg}}{\frac {\rm {m}}{{\rm {s}}^{2}}}}

where:

N: newton

kg: kilogram

m: metre

s: second.

In dimensional analysis:

{\mathsf {F}}={\frac {\mathsf {ML}}{{\mathsf {T}}^{2}}}

where

M: mass

L: length

T: time.

But, for a force of unknown type, mass or charge may be meaningless until proven applicable.

So that

{\mathsf {A}}={\mathsf {F/M}}={\frac {\mathsf {L}}{{\mathsf {T}}^{2}}},

{\mathsf {A}}={\mathsf {F/Q}}={\frac {\mathsf {L}}{{\mathsf {T}}^{2}}},

{\mathsf {P}}={\mathsf {E/M}}={\frac {{\mathsf {L}}^{2}}{{\mathsf {T}}^{2}}},

and

{\mathsf {P}}={\mathsf {E/Q}}={\frac {{\mathsf {L}}^{2}}{{\mathsf {T}}^{2}}},

where ${\mathsf {P}}$ may be called an energy phantom, or astronomical energy phantom.

Problem 1

The image is an optical negative centered on the SIMBAD coordinates J2000.0 for Van Maanen's star. Image is from the Palomar 48-inch Schmidt reflecting telescope. Van Maanen's star is the largest black dot center top right. Credit: NASA/IPAC Extragalactic Database.

The SIMBAD image is in natural color of Van Maanen's star. Credit: Aladin at SIMBAD.

In the image at right Van Maanen's star (largest dark spot) is not at the center of the coordinates where expected, but as a high proper motion star it is actually off-center to the center top right. This is an example of the change in radiation flux to a specific location of observation by a source undergoing a change in location for observation (but staying within the observation field of view) within an observable change in radiation flux (the star did not move close enough to blacken the entire frame nor change intensity sufficiently to disappear into the background of the detector).

Using a meter stick or smaller measuring device, measure the distance in mm that the star is displaced from the center of the negative. The image is 5' x 5' and may be considered from May 1.0, 1994.

According to SIMBAD, Van Maanen's star (designated VAN MAANEN STAR), is at optical coordinates: 00^h 49^m 09.902^s +05° 23' 19.01".^[6]

a. If the SIMBAD coordinates for the center of the image are the star's current position, how many milliarcseconds (mas) has the star moved since the above image was taken?

b. If the only direction of motion for the star is in the plane of the image, and the star is 14.1 ± 0.1 ly away, how fast is it moving?

c. The image at SIMBAD for the star [at left], also called Gliese 35, shows a split color image of the star (assume the position of the star is between the two color spots), where the image is 2.4' x 2.4'. The star is not at the coordinates but along the line of travel. If the star slowed down between these two images, what is its speed in the SIMBAD image?

d. Using the two speeds from above, calculate the deceleration, or acceleration, the star may have experienced.

Problem 2

In Problem 1, let the acceleration you've calculated be applied at the same magnitude over the entire time from the star's initial position to its position in the visual image at left. What is the value of the energy phantom for Van Maanen's star?

Problem 3

If the sole influence on Van Maanen's star is another star at the Sun's distance and mass, directly behind Van Maanen's star in the plane of the image, what is the force of gravity applied by this star to Van Maanen's star at its initial position in the image? Let the mass of Van Maanen's star be 0.68 ± 0.02 M_ʘ.

Is this gravitational force enough to account for the deceleration?

Problem 4

If the sole influence on Van Maanen's star is another star at the Sun's distance directly in front of Van Maanen's star in the plane of the image, what is the force of electrostatics applied by this star to Van Maanen's star at its initial position in the image? Let the charge of the star be Q_S = -0.3 x 10²⁸ e.s.u. and the amount of charge on Van Maanen's star be 0.68 ± 0.02 Q_S.

Is this electrostatic force enough to account for the deceleration?

Which is stronger, the gravitational force or the electrostatic force?

Problem 5

How much closer would the star have to be to produce the deceleration of Van Maanen's star for each force?

Furlongs per fortnight

Furlongs per fortnight is a problem set with a contained quiz that focuses on the fundamentals of observational and deductive astronomy. In the activity Energy phantoms you learned about the value of distance, or displacement, and motion, speed, velocity, and acceleration. Here, you can practice and test yourself on converting from units that may or have occurred in the literature to units popular today.

Physical units

Both physics and astronomy use units and dimensions to describe observations.

Units of Physics and Astronomy
Dimension	Astronomy	Symbol	Physics	Symbol	Conversion
time	1 day	d	1 second	s	1 d = 86,400 s^[7]
time	1 "Julian year"^[8]	J	1 second	s	1 J = 31,557,600 s
distance	1 astronomical unit	AU	1 meter	m	1 AU = 149,597,870.691 km^[7]
angular distance	1 parsec	pc	1 meter	m	1 pc ~ 30.857 x 10¹² km^[7]

Theoretical units

Perhaps the first step in deciphering ancient presumably astronomical records is determining what the unit is.

Def.

a "series of interconnected rings or links usually made of metal",^[9]
a "series of interconnected links of known length, used as a measuring device",^[9]
a "long measuring tape",^[9]
a "unit of length equal to 22 yards. The length of a Gunter's surveying chain. The length of a cricket pitch. Equal to 20.12 metres. Equal to 4 rods. Equal to 100 links.",^[9]
a "totally ordered set, especially a totally ordered subset of a poset",^[9]
iron "links bolted to the side of a vessel to bold the dead-eyes connected with the shrouds; also, the channels",^[9] or
the "warp threads of a web"^[9]

is called a chain.

Def. a "period of fourteen nights; two weeks"^[10] is called a fortnight.

Def. a "unit of length equal to 220 yards or exactly 201.168 meters, now only used in measuring distances in horse racing"^[11] is called a furlong.

Def. a "trench cut in the soil, as when plowed in order to plant a crop"^[12] or any "trench, channel, or groove, as in wood or metal"^[12] is called a furrow.

Def. the "distance that a person can walk in one hour, commonly taken to be approximately three English miles (about five kilometers)"^[13] is called a league.

Def. a "period of seven nights; a week"^[14] is called a sennight.

Def.

any "period of seven consecutive days",^[15]
a "period of seven days beginning with Sunday or Monday",^[15]
a "subdivision of the month into longer periods of work days punctuated by shorter weekend periods of days for markets, rest, or religious observation such as a sabbath",^[15] or
seven "days after (sometimes before) a specified date"^[15]

is called a week.

Problem 1

A local farmer has spotted what she believes is an astronomical object moving in the sky at night.

As the ox-plow travels using the apparently fixed points of light in the night sky, the object has covered 0.214 furlongs in her field over 1.631 fortnights.

Her field is 16.421 furlongs from horizon to horizon in the direction the object is traveling. The amount of the total sky (360° if the Earth were not in the way) her field actually views in 10.123°.

How many arcseconds has the astronomical object traversed in the night sky?

How fast is the object traveling in degrees/hour?

If after the first night of travel, the object appears to cover about 0.250 less distance, is the object accelerating or decelerating and by how much in kilometers/sec²?

If the object turns out to be 0.313 of the mean distance to the Moon away, what are its actual speed and acceleration in km and sec?

Problem 2

Like the farmer in problem 1, a sailor aboard an oil tanker heading northeast across the mid-Atlantic has noticed an apparent astronomical entity traveling north against the fixed stars. Using another nearby ship, the sailor estimates that relative to those stars the entity has traveled 20,000 leagues due north along the surface of the ocean.

Using the radius of the Earth to the North Pole, how many arcseconds has the entity traversed, if the period of movement is a tunti?

What is the entity's speed in km/sec?

What is its speed in arcsecs per minute?

At the end of the observing period, the sailor notices the entity make a 22° change in direction to the east in about four diba'igaans.

If after the change in direction the entity is observed to be traveling at the same speed, what acceleration has been applied to the entity?

Problem 3

An astronaut on the surface of the Moon is observing the Earth at night. While watching the Earth she notices a source of visible white light traveling perpendicular to the direction of the Earth's rotation.

In the time it takes North America to rotate into view from just before it's visible the source travels a linear arc approximately equivalent to the arc from the Tropic of Cancer to the Tropic of Capricorn.

About how many arcminutes has the source traveled?

If it is as far away as the Earth from the Moon, what is its speed in km/hr?

Relative to the Earth's rotational axes, is the object traveling northward or southward?

Quiz

Radiation mathematics problem set

This radiation mathematics/problem set is a series of mathematical problems that use dimensions.

Problem 1

R_{\odot }(equatorial)=696,342km

R_{J}(equatorial)=71,492km

R_{S}(equatorial)=60,268km

R_{U}(equatorial)=25,559km

R_{N}(equatorial)=24,764km

Then,

R_{J}(equatorial)=F_{J}*R_{\odot }(equatorial),

R_{S}(equatorial)=F_{S}*R_{\odot }(equatorial),

R_{U}(equatorial)=F_{U}*R_{\odot }(equatorial),

R_{N}(equatorial)=F_{N}*R_{\odot }(equatorial),

what is the value of F_J?
if R_J has 5 significant digits and R_⊙ has 6, how many significant digits should F_J have?
if the angular size of the Sun (equatorial) is 32.7', what would be the angular size of Jupiter if it were the same distance from the Earth as the Sun?
let R_S (equatorial) represent the equatorial radius of Saturn, what is the value of F_S?
if R_S has 5 significant digits and R_⊙ has 6, how many significant digits should F_S have?
what would be the angular size of Saturn if it were the same distance from the Earth as the Sun?
let R_U (equatorial) be the equatorial radius of Uranus, what is the value of F_U?
if R_U has 5 significant digits and R_⊙ has 6, how many significant digits should F_U have?
what would be the angular size of Uranus if it were the same distance from the Earth as the Sun?
let R_N (equatorial) be the equatorial radius of Neptune, what is the value of F_N?
if R_N has 5 significant digits and R_⊙ has 6, how many significant digits should F_N have?
what would be the angular size of Neptune if it were the same distance from the Earth as the Sun?
using the equatorial radii of the four gas giants (J, S, U, and N), if these four giants combined to form one approximately spherical object (T), without loss of matter and assuming each has the same particle density, what are the values of R_T and F_T?
if the object (T) is the same distance from the Earth as the Sun, what is its angular size?

Problem 2

\rho _{\odot }=1.408kg/m^{3}

\rho _{J}=1.326g/cm^{3}

\rho _{S}=0.687g/cm^{3}

\rho _{U}=1.27g/cm^{3}

\rho _{N}=1.638g/cm^{3}

\rho _{H_{2}}(0^{\circ }C,101.325kPa)=0.08988g/L

what is the density of the Sun in g/cm³?
if the standard atomic weight of hydrogen is 1.008 and there are 6.022 x 10²³ hydrogen atoms in one gram of monatomic hydrogen, how many molecules of H₂ are there in 1 gram of the diatomic gas?
if 1 L (liter) is 10^-3 m³, how many cm³ is 1 L?
if each of the classical planets is only made of diatomic hydrogen gas, how many particles of diatomic hydrogen are within each astronomical object, using the radii from problem 1?
how many diatomic hydrogen particles are in T?
using R_T, what is the H₂ particle density of T, ρ_T,H₂, in number of particles cm^-3?

Problem 3

Using the density of H₂ gas at 0°C and 101.325 kPa,

calculate the H₂ particle density for this pressure,
if the particle density scales with the inverse of the pressure, at what pressure would T have the same particle density as H₂ gas at 0°C and 101.325 kPa?
using the density of the Sun in g/cm³ calculated in Problem 2, what is the H₂ particle density for the Sun?
if the particle density scales with the inverse of the pressure, at what pressure would the Sun have the same particle density as H₂ gas at 0°C and 101.325 kPa?
what would R_T have to be so that T has the same H₂ particle density as the Sun?

Problem 4

T_J = 165 K

T_S = 135 K

T_U = 76 K

T_N = 72 K

Let the particle density scale approximately with temperature in kelvin. For example, 0°C equals 273.15 K. As the temperature increases for the same volume, the particle density remains constant but the pressure increases. In order for the temperature to have an effect, let the volume increase as the temperature increases.

the effective surface temperature of the Sun is 5778 K, use the H₂ particle density and the above temperatures to calculate the radii when these temperatures are increased to the surface temperature of the Sun.
use the new radii for the gas giants to combine them into a T', what is R_T'?
using R_T', what is its particle density and F_T'?
if the object T' is at the same distance from the Earth as the Sun, what is its angular size?

Problem 5

As temperature increases in an astronomical object composed of H₂, the molecules begin to dissociate.

"At a temperature of 8000 K, hydrogen gas is 99.99 percent monatomic."^[16]

\rho _{H}=\rho _{H_{0}}e^{E_{T}/{kT}},

where $\rho _{H_{0}}$ is an initial concentration [H] at low temperatures as partial particle density, $E_{T}$ is the dissociation energy 4.52 eV, k is Boltzmann's contant (8.6173324(78)×10⁻⁵ eV K^-1), and T is temperature in K.

Using

[H]=70400e^{-4.52/(0.00008617T)}

what is the concentration of H ([H]) at T = 8000 K?
what is [H] at T = 800 K?
at what temperature is [H] = 1?
what is [H] at T = 5778 K?

Radiation astronomy problem set

This is a visual image of beta Virginis. Its effective surface temperature is 6,132 K. Credit: Aladin at SIMBAD.

Students start from a specific observational situation, notice changes, and calculate what's happening.

An astronomical radio source is detected on January 3, 2004. Over a period of 10 hours (hrs) of observation the detector records 1,000 counts (cts). The source's position is RA 10^h 10^m 10^s Dec -10° 10' 10". Its distance is 3 AU.

Problem 1

One month later an observer looks in the same location and the source is gone. Changing telescope orientation, the observer believes she's found the same source at RA 10^h 10^m 50^s Dec -10° 10' 50". The distance to the source is still 3 AU. Over a period of 10 hrs the detector records 2,000 cts radio and 1,000 cts of submillimeter photons.

How many km has the apparent source moved?

If this second radio source is not the same as the first, what type of source is it?

If this second source is the same as the first how fast was it going?

What is the change in radio output?

Problem 2

Another month goes by before the observer can use the telescope and its detector. Of course, the source is not at either earlier position. She believes she's located it again at RA 10^h 11^m 50^s Dec -10° 10' 50". The distance to the source is still 3 AU. Over a period of 5 hrs of observation the detector records 3,000 cts of radio, 2,000 cts of submillimeter, and 1,000 cts of infrared.

How many km has it moved?

How fast was it going between position 2 and now?

What is its acceleration?

What is its radio output?

What is the acceleration in the radio output?

If the acceleration between position 2 and now occurred over the distance traveled, what is the source's energy phantom?

In terms of total photon output what is the source's acceleration in photon counts?

If this acceleration in total photon counts occurred over the entire time between position 2 and now, what is the source's photon phantom?

Problem 3

Power is said to be the rate of change of energy. The rate of change of a phantom may be called a power phantom.

Once again the observer has been given access to the telescope and its detector. She believes the source is now at RA 10^h 13^m 50^s Dec -10° 11' 50".

The distance to the source is still 3 AU. Over a period of 3 hrs of observation the detector records 3,000 cts of radio, 2,000 cts of submillimeter, 1,000 cts of infrared, and 500 cts of red.

Fortunately, a new particle counter is online, it records 200 electrons and 50 protons from the source during the same period.

Between position 3 and now,

How many km has it moved?

How fast was it going between position 3 and now?

What is its acceleration?

What is its spectral output?

What is the acceleration in the spectral output?

If the acceleration between position 3 and now occurred over the distance traveled, what is the source's energy phantom?

In terms of total photon output what is the source's acceleration in photon counts?

If this acceleration in total photon counts occurred over the entire time between position 3 and now, what is the source's photon phantom?

Using the changes in energy and photon phantoms what are the respective power phantoms.

If at position 1 and position 3 the source is the same source, but not at position 2, what kind of source is it?

What current was received from the source during the observation period?

If the resistance between the detector and the source is 15 ohms, what is the voltage between the two?

Problem 4

Power is said to be the rate of change of energy. The rate of change of a phantom may be called a power phantom.

What would a change of power be called?

Again the observer has been given access to the telescope and its detector. She believes the source is now at RA 10^h 15^m 50^s Dec -10° 11' 55".

The distance to the source is still 3 AU. Over a period of 7 hrs of observation the detector records 12,000 cts of radio, 5,000 cts of submillimeter, 4,000 cts of infrared, 2,500 cts of red, and 4,000 cts of orange.

Fortunately, a new particle counter is online, it records 400 electrons, 20 positrons, and 250 protons from the source during the same period.

Between position 4 and now,

How many km has it moved?

How fast was it going between position 4 and now?

What is its acceleration?

What is its spectral output?

What is the acceleration in the spectral output?

If the acceleration between position 4 and now occurred over the distance traveled, what is the source's energy phantom?

In terms of total photon output what is the source's acceleration in photon counts?

If this acceleration in total photon counts occurred over the entire time between position 4 and now, what is the source's photon phantom?

Using the changes in energy and photon phantoms what are the respective power phantoms.

If at position 1 and position 4 the source is the same source, but not at positions 2 or 3, what kind of source is it?

What current was received from the source during the observation period?

If the resistance between the detector and the source has changed to 35 ohms, what is the voltage between the two?

What are the current, voltage, and resistance changes?

What are the changes in the power phantoms?

Vectors and coordinates

This problem set is devoted to a variety of vector situations and coordinates for evaluation.

Problem 1

For standard basis, or unit, vectors (i, j, k) and vector components of a (a_x, a_y, a_z), what are the right ascension, declination, and value of a:

If the x-axis is the longitude of the Greenwich meridian, and a_x equals a_y, then RA equals?

If a_x equals a_y equals a_z, then the declination is?

The value of a is given by?

Problem 2

For standard basis, or unit, vectors (i, j, k) and vector components of a (a_x, a_y, a_z), what are the right ascension, declination, and value of a:

for a_x equals a_y equals a_z

If the x-axis is the longitude of the Greenwich meridian, and the object is at a_x and 2a_y, then RA equals?

a_x and 2a_y and 3a_z, then the declination is?

The value of a is given by?

Problem 3

For standard basis, or unit, vectors (i, j, k) and vector components of a (a_x, a_y, a_z), what are the right ascension, declination, and value of a:

for a_x equals a_y equals a_z

If the x-axis is the longitude of the Greenwich meridian, and the object is at 3a_x and 4a_y, then RA equals?

3a_x and 4a_y and 5a_z, then the declination is?

The value of a is given by?

Problem 4

For standard basis, or unit, vectors (i, j, k) and vector components of a (a_x, a_y, a_z), what are the right ascension, declination, and value of a:

for a_x equals 2a_y equals 3a_z

If the x-axis is the longitude of the Greenwich meridian, and the object is at 3a_x and 4a_y, then RA equals?

3a_x and 4a_y and 5a_z, then the declination is?

The value of a is given by?

Problem 5

An object has RA 10^h 10^m 10^s Dec -20° 20' 20" and r = 23 lyrs.

What are a_x, a_y, and a_z?

What are ℓ and b?

What are the ecliptic longitude and latitude?

What are J1855 and B1855?

What are J2100 and B2100?

Problem 6

An object has coordinates: 125.678 -85.678 and r = 110 pc.

What are RA and Dec?

What are a_x, a_y, and a_z?

What are ℓ and b?

What are the ecliptic longitude and latitude?

What are J1800 and B1800?

What are J2075 and B2075?

Problem 7

For standard basis, or unit, vectors (i, j, k) and vector components of a (a_x, a_y, a_z), for a_x equals 2a_y equals 3a_z:

If the x-axis is the longitude of the Greenwich meridian, and the object is at a = 3a_x and b = 4a_y, then what is

a\times b?

a\cdot b?

Problem 8

Standard basis, or unit, vectors are (i, j, k) for vector components of a (a_x, a_y, a_z).

Let a_x equal 3a_y equal 4a_z.

What are

[5a_{x},6a_{y},7a_{z}]\cdot [5a_{x},6a_{y},7a_{z}]?

If a = [5a_x, 6a_y, 7a_z] and b = [8a_x, 9a_y, 10a_z], then

a\times b?

Unknown coordinate systems

This is an optical or visual image of Aldebaran. Credit: NASA, ESA and STScI

At present the geographic coordinates on Earth of latitude and longitude translate to right ascension and declination from the Greenwich meridian and the equator as projected on the celestial sphere.

But, other records may exist even here on Earth that use specific stars or bright lights in the sky especially at night that appear fixed relative to others.

This problem set is an attempt to acquaint you with alternative coordinate systems that use standard stars such as those in constellations to preserve a record of celestial events.

From your understanding of the unusual or unknown coordinate system try to determine the target star or the likely RA and Dec intended.

Angles between known RA and Dec for two stars or other objects may be found using NASA's Object Position Finder, Coordinate Converter, and Separation Calculator.

Problem 1

A triclinic coordinate system has coordinates of different lengths (a ≠ b ≠ c) along x, y, and z axes, respectively, with interaxial angles that are not 90°. The interaxial angles α, β, and γ vary such that (α ≠ β ≠ γ). These interaxial angles are α = y⋀z, β = z⋀x, and γ = x⋀y, where the symbol "⋀" means "angle between".

An observer has spotted an unknown object in the heavens. In the location of the observer and perhaps in time, the now common RA and Dec system is not available. In order to record this object, the observer constructs a device to indicate the objects position in the heavens relative to three well-known and easily seen stars. Once three rods are in place, each pointing to a specific star the observer marks off lengths on each rod until the combination of the three lengths locates the unknown object.

With the three lengths along each axis as a_x ~ 5, a_y ~ 6, and a_z ~ 8 marked, the observer measures the three interaxial angles at α = 26°, β = 82°, and γ = 64°.

The x-axis is pointing to Achernar. The y-axis is pointing to Rigel. And, the z-axis is pointing to Aldebaran.

Using pointers attached to each rod at ninety swinging into the space between each rod, which star or stars are closest to the mutual point or points. What constellation(s) are they in. Use diagrams to justify your answer.

What is the RA Dec of the target?

Problem 2

In a monoclinic coordinate system, a ≠ b ≠ c, and depending on setting α = β = 90° ≠ γ, α = γ = 90° ≠ β, α = 90° ≠ β ≠ γ, or α = β ≠ γ ≠ 90°.

As in problem 1, an observer has spotted a luminous object and is attempting to fix its location in the sky using known stars.

The x-rod is pointing at Beta Librae (Zubeneschamali). The y-rod points at epsilon Ursa Major (eps UMa). And, the z-rod points at Altair. The angle between y and z is approximately 90°. Between z and x, β = 78°. Between x and z, γ = 76°. The angled pointers are 6 units along the x-axis and 8 units along the y and z-axes.

What constellation is the target object in?

What star or stars may be the target?

What is the RA Dec of the target?

Problem 3

An observer has located an object of interest using Betelgeuse, Arcturus, and Spica at equal units along each rod. What are the angles between the axes and the RA and Dec of the object?

Problem 4

An observer has spotted the Large Magellanic Cloud, find three stars to set up a coordinate system.

What are the angles between your three stars and the approximate units to pinpoint the LMC?

What is the RA Dec of your three stars?

Problem 5

In an orthorhombic coordinate system α = β = γ = 90° and a ≠ b ≠ c.

An observer has located an object of interest at proportionately a = 6, b = 5, and c = 7 units along axes pointed at Altair, Alioth (epsilon Ursa Major, eps UMa), and Betelgeuse, where the angles between these stars are all approximately 90°.

What is the possible object of interest?

What are the errors on the angles between these stars?

What constellations are each star in?

What is the RA Dec of the target?

Locate three other bright stars that have interaxial angles of 90°.

Problem 6

A tetragonal coordinate system has α = β = γ = 90°, and a = b ≠ c.

Using Betelgeuse, Altair, an epsilon Ursa Major (Alioth), an observer has decided an object of interest has axes proportional units of 6 = a = b, c = 2.

What is the likely object and its RA and Dec?

What constellation is it in?

Problem 7

A rhombohedral system has a = b = c and α = β = γ < 120°, ≠ 90°.

Find three bright stars in which α = β = γ < 120°, ≠ 90°.

Find an object relative to these three stars where a = b = c, approximately.

Problem 8

A hexagonal system has a = b ≠ c and α = β = 90°, γ = 120°.

Find three stars where α = β = 90°, γ = 120°. For example, Polaris and Delta Orionis (Mintaka) are 90° apart.

Locate an object along these three rods where proportionately a = b ≠ c.

Unusual units

This problem set like furlongs per fortnight deals with unusal or what may seem to be less common or seldom used units. The challenge is to convert the astronomers/observers findings into more common units. You may need to locate definitions of either to determine how to setup and solve the problem.

Problem 1

A farmer has been reading several of the lectures on Wikiversity about radiation astronomy. He has several acres of clover that will not be planted for at least six months. Having become enthusiastic about neutron astronomy he decides to build an acre-sized neutron detector over a one-acre area in a clover field.

Each of his 38 detectors is exactly 100 arshin on a side. He has judiciously designed each so that the direction as well as the energy of each incoming neutron can be determined. He has attached the best pulse-counting electronics he can purchase.

Each detector has been carefully placed level to the ground within 23.3'. But, because his field isn't perfectly level he places his collection of level detectors throughout 1.47 acre-feet.

Each of these detectors has about its own area between itself and the next detector so that some light gets through to grow his clover.

Next, he estimates that his total dedicated detector field samples 64.7 % of the sky over head, which in turn due to local geography is probably not more than 7.63 % of the total celestial sphere.

When he has sufficient power to run the detector, he turns on the array and collects as many neutron counts as possible. Because he has directional determination, neutrons from below the detectors are not counted. During 2 h 12 m 8 s of counting he records a total of 1023 neutrons. At another time later, he counts for 3 h 28 m 16 s and records 4435 neutrons. A third counting period of 1 h 57 m yields 768 neutrons.

From the above information, what is the average neutron flux in neutrons cm^-2 s^-1 sr^-1?

If the average energy of each neutron is 150 MeV, what is the average wavelength in nm?

Problem 2

The significant other of the farmer in Problem 1 stops by upon occasion and has become interested in neutrons.

She has discovered a unit called a barn. Using the unit she calculates the radius, approximate surface area, and volume of a ²³⁸U nucleus. Calculate these yourself.

As the neutrons in problem 1 are being accelerated through the detector by gravity, what is the neutron pressure over the average surface area of the detector?

What is the neutron pressure in bars?

Problem 3

How fast are the neutrons going on average as they go through or into the detector?

How fast in knots?

How fast in furlongs per fortnight?

Problem 4

A hydrogen atom is about 0.11 nm in diameter.

The "relative motion in a hydrogen atom in crossed electric and magnetic fields leads to peculiar quasi-ionized states with an electron localized very far from a proton."^[17] Let this peculiar quasi-ionized state be about the diameter of a hydrogen atom.

What is the electric dipole moment of such a hydrogen atom?

If this state or something similar existed within a neutron, what would be the neutron's electric dipole moment?

Problem 5

If a neutrino is subject to an electric dipole moment formed in the same way as described above for a hydrogen atom, what is the electric dipole moment of a neutrino?

Let a neutrino be on the order of an electron in size; i.e., a radius of 2.8 x 10^-15 m.

What is the electric dipole moment of a neutrino in Coulomb meters?

Some units

Def. a "unit of surface area (symbol a. or ac.), originally as much as a yoke of oxen could plough in a day; later defined as an area 1 chain (22 yd) by 1 furlong (220 yd), or 4,840 square yards. Equivalent to about 4,046.86 square metres."^[18] is called an acre.

Def. a "unit of volume equal to an acre times a foot, about 1233.5 kiloliters, or 66 feet by 660 feet by 1 foot"^[19] is called an acre-foot.

Def. "the force associated with a magnetic field and that produces magnetic flux; it is the work required to carry a magnetic monopole of unit strength once round a magnetic circuit; measured in ampere-turns"^[20] is called a magnetomotive force.

Def. "the unit of magnetomotive force"^[21] is called an ampere-turn.

Def. a "specific gravity scale measuring the relative density of various petroleum liquids, expressed in degrees"^[22] is called an API gravity, where API may stand for the American Petroleum Institute.

Def. a "Russian length unit, equal to 71.12 centimeters"^[23] is called an arshin.

A barn (symbol b) is a unit of area. A barn is defined as 10⁻²⁸ m² (100 fm²) and is approximately the cross sectional area of a uranium nucleus.

Conversion to SI units
Unit	Symbol	m²	cm²
megabarn	Mb	10⁻²²	10⁻¹⁸
kilobarn	kb	10⁻²⁵	10⁻²¹
barn	b	10⁻²⁸	10⁻²⁴
millibarn	mb	10⁻³¹	10⁻²⁷
microbarn	μb	10⁻³⁴	10⁻³⁰
nanobarn	nb	10⁻³⁷	10⁻³³
picobarn	pb	10⁻⁴⁰	10⁻³⁶
femtobarn	fb	10⁻⁴³	10⁻³⁹
attobarn	ab	10⁻⁴⁶	10⁻⁴²
zeptobarn	zb	10⁻⁴⁹	10⁻⁴⁵
yoctobarn	yb ^[24]^[25]	10⁻⁵²	10⁻⁴⁸

Def. the "rate of transfer of energy (or another physical quantity) through a given surface, specifically electric flux, magnetic flux"^[26] is called a flux.

Def. a "unit of pressure equal to 100 pascals"^[27] is called a millibar.

Def. a "unit of speed, equivalent to one nautical mile per hour"^[28] is called a knot.

Def. a "unit of length corresponding approximately to one minute of arc of latitude along any meridian"^[29] is called a nautical mile.

Def. the "amount of electrostatic potential between two points in space"^[30] is called a voltage.

Def. the "time rate of flow of electric charge"^[31] is called a current.

Def. the "opposition offered by an electrical conductor to the flow of a current through itself, resulting in a conversion of electrical energy into heat and radiation"^[32] is called a resistance.

Telescopes and cameras

In most photography and all telescopy, where the subject is essentially infinitely far away, longer focal length (lower optical power) leads to higher magnification and a narrower angle of view; conversely, shorter focal length or higher optical power is associated with a wider angle of view.

Problem 1

This is a double-convex, thick lens diagram. Credit: .

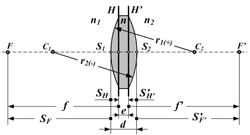
For the case of a double-convex lens of thickness d in air, and surfaces with radii of curvature R₁ and R₂, the effective focal length f is given by:

{\frac {1}{f}}=(n-1)\left[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-1)d}{nR_{1}R_{2}}}\right],

where n is the refractive index of the lens medium. The quantity 1/f is also known as the optical power of the lens.

What is the formula for a plano-convex lens?

Calculate the focal length of a double convex lens in which R₁ = 10 m and R₂ = 200 m. Let n = 1.732 and d = 2 cm.

What is the focal length of a hemispherical plano-convex lens of radius 10 m? Let n= 1.324 and d = 1 dm.

What is a likely focal length for a plano-convex lens where the convex surface is parabolic rather than spherical?

Problem 2

The f-number (sometimes called focal ratio, f-ratio, f-stop, or relative aperture^[33]) of an optical system is the ratio of the [optical] lens's focal length to the diameter of the entrance pupil [or aperture].^[34]

The f-number N is given by

N={\frac {f}{D}}\

where $f$ is the focal length, and $D$ is the diameter of the entrance pupil (effective aperture). It is customary to write f-numbers preceded by $f/$ ,^[34] which forms a mathematical expression of the entrance pupil diameter in terms of $f$ and N. For example, if a lens's focal length is 10 mm and its entrance pupil diameter is 5 mm, the f-number is 2 and the aperture size would be expressed as $f/2$ .

The brightness of the projected image (illuminance) relative to the brightness of the scene in the lens's field of view (luminance) decreases with the square of the f-number. Doubling the f-number decreases the relative brightness by a factor of four. To maintain the same photographic exposure when doubling the f-number, the exposure time would need to be four times as long.

An adjustable diaphragm changes the size of the aperture stop and thus the entrance pupil size. The entrance pupil diameter is not necessarily equal to the aperture stop diameter, because of the magnifying effect of lens elements in front of the aperture.

A 100 mm focal length f/4 lens has an entrance pupil diameter of 25 mm. A 200 mm focal length f/4 lens has an entrance pupil diameter of 50 mm. The 200 mm lens's entrance pupil has four times the area of the 100 mm lens's entrance pupil, and thus collects four times as much light from each object in the lens's field of view. But compared to the 100 mm lens, the 200 mm lens projects an image of each object twice as high and twice as wide, covering four times the area, and so both lenses produce the same illuminance at the focal plane when imaging a scene of a given luminance.

For a focal length of 100 mm, what are the aperture or entrance pupil diameters for each of the apertures shown if no optical components are between the entrance pupil and the aperture?

For a simple camera or telescope with an aperture lens diameter of 5 m, what is the focal length for each of the apertures or entrance pupil diameters in the diagram if no optical components are between the entrance pupil and the aperture?

For the following pairs of focal lengths and lens diameters, what would be the f-numbers? (a) 5 m, 3 m (b) 10 m, 3 mm (c) 50 cm, 2 m (d) 15 km, 25 m (e) 5,000 km, 16 cm.

Consider the calculations needed to build an optical telescope.

Problem 3

The lens in the image at right has an aperture range of $f/2.0$ to $f/22.$

The image lens at right uses a standard f-stop scale, which is an approximately geometric sequence of numbers that corresponds to the sequence of the powers of the square root of 2: $f/1,$ $f/1.4$ $f/2,$ $f/2.8,$ $f/4,$ $f/5.6,$ $f/8,$ $f/11,$ $f/16,$ [and] $f/22.$

The sequence above is obtained by approximating the following exact geometric sequence:

f/1={\frac {f/1}{({\sqrt {2}})^{0}}},

f/1.4={\frac {f/1}{({\sqrt {2}})^{1}}},

f/2={\frac {f/1}{({\sqrt {2}})^{2}}},

f/2.8={\frac {f/1}{({\sqrt {2}})^{3}}},

f/4=,

f/5.6=,

f/8=,

f/11=,

f/16=,

f/22=.

What are the missing terms?

Each "stop" is marked with its corresponding f-number, and represents a halving of the light intensity from the previous stop. This corresponds to a decrease of the pupil and aperture diameters by a factor of 1/ $\scriptstyle {\sqrt {2}}$ or about 0.7071, and hence a halving of the area of the pupil.

For a lens diameter of 35 mm, what is the focal length for each f-stop?

Problem 4

Shutter speeds are arranged so that each setting differs in duration by a factor of approximately two from its neighbour. Opening up a lens by one stop allows twice as much light to fall on the film in a given period of time. Therefore to have the same exposure at this larger aperture as at the previous aperture, the shutter would be opened for half as long (i.e., twice the speed). The film will respond equally to these equal amounts of light, since it has the property of reciprocity. This is less true for extremely long or short exposures, where we have reciprocity failure. Aperture, shutter speed, and film sensitivity are linked: for constant scene brightness, doubling the aperture area (one stop), halving the shutter speed (doubling the time open), or using a film twice as sensitive, has the same effect on the exposed image.

Shutter speed or exposure time is the length of time a camera's shutter is open when taking a photograph.^[35] The amount of light that reaches the film or image sensor is proportional to the exposure time.

Exposure value (EV) is a single quantity that accounts for the shutter speed and the f-number.

Multiple combinations of shutter speed and f-number can give the same exposure value.

Doubling the exposure time doubles the amount of light (subtracts 1 EV). Making the f-number one stop brighter (reducing the f-number by a factor of $\scriptstyle {\sqrt {2}}$ ) also doubles the amount of light. A shutter speed of 1/50 s with an $f/4.0$ lens gives the same exposure value as a 1/100 s shutter with an { $f/2.8$ lens, and also the same exposure value as a 1/200 s shutter with an $f/2.0$ lens.

A standardized 2:1 scale for shutter speed is such that opening one aperture stop and reducing the shutter speed by one step resulted in the identical exposure. The standards for shutter speeds are:^[36]

1/16000 s
1/12000 s
1/8000 s
1/4000 s
1/2000 s
1/1000 s
1/500 s
1/250 s
1/125 s
1/60 s
1/30 s
1/15 s
1/8 s
1/4 s
1/2 s
1 s

What are the other f-numbers that match the shutter speeds?

Exposure value (EV) is a number that represents a combination of a camera's shutter speed and f-number, such that all combinations that yield the same exposure have the same EV value (for any fixed scene luminance). Exposure value also is used to indicate an interval on the photographic exposure scale, with 1 EV corresponding to a standard power-of-2 exposure step, commonly referred to as a stop.

Exposure value is a base-2 logarithmic scale:

\mathrm {EV} =\log _{2}{\frac {N^{2}}{t}}\,,

where

N is the relative aperture (f-number)
t is the exposure time (“shutter speed”) in seconds.

In a mathematical expression involving physical quantities, it is common practice to require that the argument to a transcendental function (such as the logarithm) be dimensionless. The definition of EV ignores the units in the denominator and uses only the numerical value of the exposure time in seconds; EV is not the expression of a physical law, but simply a number for encoding combinations of camera settings.

Match up the shutter speeds with f-numbers to give the same EV.

Angular momentum and energy

This diagram describes the relationship between force (F), torque (τ), momentum (p), and angular momentum (L) vectors in a rotating system. 'r' is the radius. Credit: .

Angular momentum and energy are concepts developed to try to understand everyday reality.

An angular momentum L of a particle about an origin is given by

\mathbf {L} =\mathbf {r} \times \mathbf {p}

where r is the radius vector of the particle relative to the origin, p is the linear momentum of the particle, and × denotes the cross product (r · p sin θ). Theta is the angle between r and p.

Fundamentals

Def. a "quantity [...] cohering together so as to make one body, or an aggregation of particles or things which collectively make one body or quantity"^[37] is called a mass.

Mass is an idea.

Def. a "property of a body that resists any change to its uniform motion"^[38] is called inertia.

Mass and inertia are generally considered equivalent.

Isaac Newton's laws of motion contain the idea of inertia.

Newton's First law: "Every body persists in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by force impressed."^[39]

While motion in a straight line, or rectilinear motion can be produced over limited distances in a laboratory, it may not occur naturally.

Def. "the product of [a body's] mass and velocity"^[40] is called momentum.

Def. "the rotary inertia of a system [such as] an isolated rigid body [...] is a measure of the extent to which an object will continue to rotate in the absence of an applied torque"^[41] is called angular momentum.

Def. a "rotational or twisting effect of a force"^[42] is called a torque.

Def. a "turning effect of a force applied to a rotational system at a distance from the axis of rotation"^[43] is called a moment of force.

"The moment is equal to the magnitude of the force multiplied by the perpendicular distance between its line of action and the axis of rotation."^[43]

A torque and a moment of force are the same. Each is a "unit of work done, or energy expended"^[44]

For an object with a fixed mass that is rotating about a fixed symmetry axis, the angular momentum is expressed as the product of the moment of inertia of the object and its angular velocity vector:

\mathbf {L} =I{\boldsymbol {\omega }}

where I is the moment of inertia of the object (in general, a tensor quantity), and ω is the angular velocity.

The moment of inertia is the mass property of a rigid body that defines the torque needed for a desired angular acceleration about an axis of rotation. Moment of inertia depends on the shape of the body and may be different around different axes of rotation. A larger moment of inertia around a given axis requires more torque to increase the rotation, or to stop the rotation, of a body about that axis. Moment of inertia depends on the amount and distribution of its mass, and can be found through the sum of moments of inertia of the masses making up the whole object, under the same conditions.

In two dimensions the angular velocity ω is given by

\omega ={\frac {d\phi }{dt}}

This is related to the cross-radial (tangential) velocity by:^[45]

\mathrm {v} _{\perp }=r\,{\frac {d\phi }{dt}}

An explicit formula for v_⊥ in terms of v and θ is:

\mathrm {v} _{\perp }=|\mathrm {\mathbf {v} } |\,\sin(\theta )

Combining the above equations gives a formula for ω:

\omega ={\frac {|\mathrm {\mathbf {v} } |\sin(\theta )}{|\mathrm {\mathbf {r} } |}}

Problem 1

This is a visual image of the Sun with some sunspots visible on the photosphere. The two small spots in the middle have about the same diameter as our planet Earth. Credit: NASA.

Using the following values, and considering the Sun to be a rigid, solid object, answer the questions below. $R_{\odot eq}=696342km,$ $M_{\odot }=1.9891\times 10^{30}kg,$ and $V_{eqrot}=7.189\times 10^{3}km/h.$

What is the angular velocity of the Sun?

What is its moment of inertia?

What is the Sun's angular momentum?

Estimate how much torque is necessary to bring the Sun's rotational velocity down to zero?

What are the units of angular momentum for the Sun?

Problem 2

Using the following values, and considering the Jupiter to be a rigid, solid object, answer the questions below. $R_{Jeq}=71492km,$ $M_{J}=1.8986\times 10^{27}kg,$ and $V_{eqJ}=4.53\times 10^{4}km/h.$

What is the angular velocity of the Jupiter?

What is its moment of inertia?

What is the Jupiter's angular momentum from rotation?

Estimate how much torque is necessary to bring the Jupiter's rotational velocity down to zero?

Using a mean orbital radius between 8.16 x 10⁸ km and 7.41 x 10⁸ km, what's its angular momentum from revolution around the Sun?

Is the total angular momentum of Jupiter greater than the Sun's?

Problem 3

Using the following values, and considering the Jupiter to be a rigid, solid object, answer the questions below. $R_{Seq}=60268km,$ $M_{S}=5.6846\times 10^{24}kg,$ and $V_{eqS}=3.55\times 10^{4}km/h.$

What is the angular velocity of the Saturn?

What is its moment of inertia?

What is the Saturn's angular momentum from rotation?

Estimate how much torque is necessary to bring the Saturn's rotational velocity down to zero?

Using a mean orbital radius between 1.51 x 10⁹ km and 1.35 x 10⁹ km, what's its angular momentum from revolution around the Sun?

Is the total angular momentum of Saturn greater than the Sun's?

Problem 4

This is an image of the planet Uranus taken by the spacecraft Voyager 2 in 1986. Credit: NASA/JPL/Voyager mission.

Using the following values, and considering the Jupiter to be a rigid, solid object, answer the questions below. $R_{Ueq}=60268km,$ $M_{U}=5.6846\times 10^{24}kg,$ and $V_{eqU}=3.55\times 10^{4}km/h.$

What is the angular velocity of the Uranus?

What is its moment of inertia?

What is the Uranus's angular momentum from rotation?

Estimate how much torque is necessary to bring the Uranus's rotational velocity down to zero?

Using a mean orbital radius between 3.00 x 10⁹ km and 2.75 x 10⁹ km, what's its angular momentum from revolution around the Sun?

Is the total angular momentum of Uranus greater than the Sun's?

Problem 5

Using the following values, and considering the Jupiter to be a rigid, solid object, answer the questions below. $R_{Neq}=24764km,$ $M_{N}=1.0243\times 10^{26}kg,$ and $V_{eqN}=9.66\times 10^{4}km/h.$

What is the angular velocity of the Neptune?

What is its moment of inertia?

What is the Neptune's angular momentum from rotation?

Estimate how much torque is necessary to bring the Neptune's rotational velocity down to zero?

Using a mean orbital radius between 4.55 x 10¹⁰ km and 4.45 x 10¹⁰ km, what's its angular momentum from revolution around the Sun?

Is the total angular momentum of Neptune greater than the Sun's?

Angular momentum in electrodynamics

When describing the motion of a charged particle in an electromagnetic field [use] the canonical momentum P. P includes a contribution from the electric potential Φ(r,t) and vector potential A(r,t)

The canonical angular momentum L = r × P is given by

\mathbf {p} =m\mathbf {v} =\mathbf {P} -e\mathbf {A}

where e is the electric charge of the particle and A the magnetic vector potential of the electromagnetic field.

The Gauge theory angular momentum is given by

\mathbf {K} =\mathbf {r} \times (\mathbf {P} -e\mathbf {A} ).

Spin

What is a spin of 1/2?

Cosmic circuits

Voyager 1 has found only electrons streaming into the heliosphere from elsewhere in the galaxy. This problem set poses several problems to calculate the possibility that a simple electrical circuit is involved.

Circuits

The diagram at right suggests a simple electrical circuit.

Def. an enclosed "path of an electric current"^[46] is called a circuit.

In the diagram at right are three components:

a voltage (V), or current (i), source,
an enclosed path, and
a resistance, or resistor, (R).

According to Ohm's law:

V=iR.

With respect to an enclosed path, consider a path from outside the heliosphere, inward toward the Sun, and out again. Let the incoming electrons have 500 MeV of energy and a flux of 8.5 x 10⁴ e^- cm^-2 s^-1.

Def. a "time rate of flow of electric charge"^[31] is called a current.

Def. "that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 metre apart in vacuum, would produce between these conductors a force equal to 2 x 10^–7 newton per metre of length"^[47] is called an ampere.

Def. an "amount of electrostatic potential between two points in space"^[30] is called a voltage.

Problem 1

This is an image of a 105 W halogen light bulb. Credit: Reinraum.

Using the energy and electron flux described above, what is the apparent current in Amperes (A), flowing toward the Sun?

Considering the Sun to be a natural light source like the halogen light bulb at right, what is the resistance (R) and the voltage (V) of this circuit?

Problem 2

If the luminosity (in Watts, W) of the Sun is 3.846 x 10²⁶ W, pick a combination of resistance (R) and voltage (V) for this circuit.

Problem 3

If the total number of protons being carried away from the Sun by the solar wind is about 1.3×10³⁶ per second, with 10 keV of energy, what is the proton (p⁺) flux away from the Sun?

What is the amperage (A) of this solar wind?

Pick a combination of resistance (R) and voltage (V) for this circuit for the luminosity of the Sun.

Problem 4

Using your electron and proton currents calculated above, where the current vector toward the Sun is the same as away from the Sun as part of the circuit, does the proton current increase or decrease the total current?

In a household circuit, the voltage may be 110 V and the current 15 A, considering it a direct current circuit, what is the number of electrons per second for these 15 Amps?

If the Sun is a 110 V source, and the number of electrons leaving the Sun in all directions is 15 Amps, what is the resistance of the enclosed path?

Problem 5

The Voyager 1 data suggests that no electrons or protons are leaving the heliosphere into the galaxy. Some of the incoming electrons may be converted into neutrons. Some are being turned back toward the Sun as part of the circuit. If ten per cent of the incoming interstellar electrons are those leaving the Sun and being turned back toward the Sun, and another portion are being neutralized by the proton solar wind, what is the maximum number that may be turned into neutrons if no electrons are lost and only their energy is used to make the Sun luminescent?

If the only electrons leaving the Sun have the same numbers and energy of the protons leaving the Sun, how many electrons are being turned into radiant energy, if 50 % are being turned into neutrons?

If the radiant energy leaving the Sun combines with incoming interstellar gamma-rays at 500 MeV or greater, what gamma-ray flux is needed to complete the circuit if half are converted to electrons?

Columns

A column density is the number of units of matter observed along a line of sight that has an area of observation. This area has a height that is the distance to, or through which observation is taking place, an object.

"A region of the sky [at the right] called the "Lockman Hole", located in the constellation of Ursa Major, is one of the areas surveyed in infrared light by the Herschel Space Observatory. All of the little dots in this picture are distant galaxies. The pattern of their collective light is what's known as the cosmic infrared background. By studying this pattern, astronomers were able to measure how much dark matter it takes to create a galaxy bursting with young stars."^[48]

Column density

Def. a "total amount per unit area of a material suspended in a fluid or in a cloud in space, measured along the length of a column"^[49] is called a column density.

Usage notes:

"Quoted in terms of mass per (cross-sectional) area, or number per area".^[49]

Lockman Hole

"We have made a detailed 21 cm study of areas that have the smallest known amount of H I in the northern sky. These observations were corrected for stray radiation using a method described in an Appendix and have an estimated uncertainty in N_{H I} of ≤ 5 x 10¹⁸ cm^-2. The region of main interest, around α = 10^h45^m, δ = 57°20', has a minimum N_{H I} of 4.5 x 10¹⁹ cm^-2."^[50]

Probably "most of the [neutral] hydrogen is extended and not contained in very small, unresolved, clouds. For example, there would have to be ~100 small clouds in the ~0.2 deg² of the 43 m beam to produce the observed σ/〈N_{H I}〉≈ 0.1. At a distance of 100 pc, each would have a diameter ~0.1 pc and a density 〈n〉~ 200 cm^-3."^[50]

Problem 1

Using the numbers in the above section for the beam diameter at the antenna, the circular area at 100 pc, the number of clouds and the neutral hydrogen particle density, calculate the column density along the line of sight and compare it to the column density.

Problem 2

Using the uncertainty in the column density, calculate the approximate uncertainty in the hydrogen density.

Problem 3

Using the column density for the Lockman Hole, calculate the apparent neutral hydrogen flux in units of m^-2 sr^-1. Calculate the uncertainty in units of flux.

Problem 4

In regions like the Lockman Hole "the dust particles are small (radii a < 0.25 m)".^[51] The dust column density (D^T) is 0.44 MJy sr^-1 so that the D^T/N(H I) = 0.077.^[51]

Using this information, calculate the dust column density in number of dust grains cm^-2.

Problem 5

According to SIMBAD there are some 1217 objects within 30' radius of the centered position for the Lockman Hole. Although these are mostly astronomical infrared sources and galaxies, if these are large dust particles, calculate their column density.

Of these only 349 are X-ray sources, calculate their column density.

Spectrographs

File:AstroSurf Instrumentation.jpg

The image shows a cap-off view of the insides of a spectrograph. Credit: Buil/AstroSurf.

This problem set is designed for astronomy to help the student, teacher, and researcher understand the inner workings of a spectrograph.

Spectrography

Def. a "machine for recording spectra, producing spectrograms"^[52] is called a spectrograph.

Def. a "visual representation of the spectrum of a celestial body's radiation"^[53] is called a spectrogram.

A prism is a transparent optical element with flat, polished surfaces that refract light over a range of wavelengths. At least two of the flat surfaces must have an angle α between them. The exact angles between the surfaces depend on the application. The traditional geometrical shape is that of a triangular prism with a triangular base and rectangular sides, and in colloquial use "prism" usually refers to this type.

Ray angle deviation and dispersion through a prism can be determined by tracing a sample ray through the element and using Snell's law at each interface. For the prism shown at right, the indicated angles are given by

{\begin{aligned}\theta '_{0}&=\,{\text{arcsin}}{\Big (}{\frac {n_{0}}{n_{1}}}\,\sin \theta _{0}{\Big )}\\\theta _{1}&=\alpha -\theta '_{0}\\\theta '_{1}&=\,{\text{arcsin}}{\Big (}{\frac {n_{1}}{n_{2}}}\,\sin \theta _{1}{\Big )}\\\theta _{2}&=\theta '_{1}-\alpha \end{aligned}}

.

For a prism in air $n_{0}=n_{2}\simeq 1$ . Defining $n=n_{1}$ , the deviation angle $\delta$ is given by

\delta =\theta _{0}+\theta _{2}=\theta _{0}+{\text{arcsin}}{\Big (}n\,\sin {\Big [}\alpha -{\text{arcsin}}{\Big (}{\frac {1}{n}}\,\sin \theta _{0}{\Big )}{\Big ]}{\Big )}-\alpha

If the angle of incidence $\theta _{0}$ and prism apex angle $\alpha$ are both small, $\sin \theta \approx \theta$ and ${\text{arcsin}}x\approx x$ if the angles are expressed in radians. This allows the nonlinear equation in the deviation angle $\delta$ to be approximated by

\delta \approx \theta _{0}-\alpha +{\Big (}n\,{\Big [}{\Big (}\alpha -{\frac {1}{n}}\,\theta _{0}{\Big )}{\Big ]}{\Big )}=\theta _{0}-\alpha +n\alpha -\theta _{0}=(n-1)\alpha \ .

The deviation angle depends on wavelength through n, so for a thin prism the deviation angle varies with wavelength according to

\delta (\lambda )\approx [n(\lambda )-1]\alpha

.

Problem 1

The image at the top of this resource appears to have a deviation angle of 45°. The detector may be about 4 cm from the prism. Using a refractive index n = 1.732 and a representative wavelength for the optical colors calculate the width of each wavelength channel and the total detector width to capture the incoming photons. Use an apex angle of 35°.

Problem 2

Let the deviation angle be 30°, the detector distance be half a meter with the same refractive index and apex angle of 37.5°.

For the optical colors calculate the width of each wavelength channel and the total detector width to capture the incoming photons.

Problem 3

Using the configuration of Problem 2 and assuming a prism for X-rays and gamma rays existed, calculate the width of each wavelength channel, for five representative wavelengths of each, and the total detector width to capture the incoming photons.

Problem 4

Using the configuration of Problem 1 and representative wavelengths for each of the infrared bands described in infrared astronomy, calculate the width of each wavelength channel and the total detector width to capture the incoming photons.

Problem 5

Using each configuration of the problems above and representative wavelengths for submillimeter, microwave, and radio waves, calculate the width of each wavelength channel and the total detector width to capture the incoming photons.

Planck's equation

Planck's equation describes the amount of spectral radiance at a certain wavelength radiated by a black body in thermal equilibrium.

Electromagnetic radiation

In terms of wavelength (λ), Planck's [equation] is written as

B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\mathrm {B} }T}}-1}}

where B is the spectral radiance, T is the absolute temperature of the black body, k_B is the Boltzmann constant, h is the Planck constant, and c is the speed of light.

This form of the equation contains several constants that are usually not subject to variation with wavelength. These are h, c, and k_B. They may be represented by simple coefficients: c1 = 2h c² and c2 = h c/k_B.

By setting the first partial derivative of Planck's equation in wavelength form equal to zero, iterative calculations may be used to find pairs of (λ,T) that to some significant digits represent the peak wavelength for a given temperature and vice versa.

{\frac {\partial B}{\partial \lambda }}={\frac {c1}{\lambda ^{6}}}{\frac {1}{e^{\frac {c2}{\lambda T}}-1}}[{\frac {c2}{\lambda T}}{\frac {1}{e^{\frac {c2}{\lambda T}}-1}}e^{\frac {c2}{\lambda T}}-5]=0.

Or,

{\frac {c2}{\lambda T}}{\frac {1}{e^{\frac {c2}{\lambda T}}-1}}e^{\frac {c2}{\lambda T}}-5=0.

{\frac {c2}{\lambda T}}{\frac {1}{e^{\frac {c2}{\lambda T}}-1}}e^{\frac {c2}{\lambda T}}=5.

Use c2 = 1.438833 cm K.

Problem 1

For the wavelength, temperature pair (570 nm, 5260 K), and for a simple calculator,

y=(1.48833/(0.0000570*5260))*exp(1.48833/(0.0000570*5260))/(exp(1.48833/(0.0000570*5260))-1)-5, followed by print y, yields a value close to zero (-1.006663E-03). The closer to zero the more accurate the estimate.

sRGB rendering of the spectrum of visible light
Color	Frequency	Wavelength
violet	668–789 THz	380–450 nm
blue	631–668 THz	450–475 nm
cyan	606–630 THz	476–495 nm
green	526–606 THz	495–570 nm
yellow	508–526 THz	570–590 nm
orange	484–508 THz	590–620 nm
red	400–484 THz	620–750 nm

For each color band, pick a wavelength, and calculate the corresponding temperature to complete the pair.

Problem 2

The table below gives approximate ultraviolet wavelength bands. Pick a wavelength from each and calculate the corresponding temperature to complete the pair.

Name	Abbreviation	Wavelength range in nanometers	Energy per photon
Before UV spectrum	Visible light	above 400 nm	below 3.10 eV
Ultraviolet A, long wave, or black light	UVA	400 nm–315 nm	3.10–3.94 eV
Near	NUV	400 nm–300 nm	3.10–4.13 eV
Ultraviolet B or medium wave	UVB	315 nm–280 nm	3.94–4.43 eV
Middle	MUV	300 nm–200 nm	4.13–6.20 eV
Ultraviolet C, short wave, or germicidal	UVC	280 nm–100 nm	4.43–12.4 eV
Far	FUV	200 nm–122 nm	6.20–10.2 eV
Vacuum	VUV	200 nm–100 nm	6.20–12.4 eV
Low	LUV	100 nm–88 nm	12.4–14.1 eV
Super	SUV	150 nm–10 nm	8.28–124 eV
Extreme	EUV	121 nm–10 nm	10.2–124 eV
Beyond UV range	X-rays	below 10 nm	above 124 eV

Problem 3

X-rays span 3 decades in wavelength, frequency and energy. From 10 to 0.1 nanometers (nm) (about 0.12 to 12 keV) they are classified as soft X-rays, and from 0.1 nm to 0.01 nm (about 12 to 120 keV) as hard X-rays.

Super soft X-rays have energies in the 0.09 to 2.5 keV.

For each of the types of X-rays, pick a representative wavelength and calculate the temperature to complete the pair.

Gamma rays have wavelengths less than 10 picometers (less than the diameter of an atom).

10¹⁵ Hz = PHz petahertz

10¹⁸ Hz = EHz exahertz

10²¹ Hz = ZHz zettahertz

10²⁴ Hz = YHz yottahertz

Convert these frequencies to their corresponding wavelengths and calculate the temperature for each to complete the pair.

Problem 4

Astronomers often divide the infrared spectrum as follows:^[54]

Designation	Abbreviation	Wavelength
Near Infrared	NIR	(0.7–1) to 5 µm
Mid Infrared	MIR	5 to (25–40) µm
Far Infrared	FIR	(25–40) to (200–350) µm.

These are the approximate ranges for photon energies of the infrared bands:

Division Name	Wavelength	Photon Energy
Near-infrared	0.75-1.4 µm	0.9-1.7 eV
Short-wavelength infrared	1.4-3 µm	0.4-0.9 eV
Mid-wavelength infrared	3-8 µm	150-400 meV
Long-wavelength infrared	8–15 µm	80-150 meV
Far infrared	15 - 1,000 µm	1.2-80 meV

These are the main infrared atmospheric windows:

Wavelength range (micrometres)	Astronomical bands	Telescopes
0.65 to 1.0	R and I bands	All major optical telescopes
1.1 to 1.4	J band	Most major optical telescopes and most dedicated infrared telescopes
1.5 to 1.8	H band	Most major optical telescopes and most dedicated infrared telescopes
2.0 to 2.4	K band	Most major optical telescopes and most dedicated infrared telescopes
3.0 to 4.0	L band	Most dedicated infrared telescopes and some optical telescopes
4.6 to 5.0	M band	Most dedicated infrared telescopes and some optical telescopes
7.5 to 14.5	N band	Most dedicated infrared telescopes and some optical telescopes
17 to 25	Q band	Some dedicated infrared telescopes and some optical telescopes
28 to 40	Z band	Some dedicated infrared telescopes and some optical telescopes
330 to 370		Some dedicated infrared telescopes and some optical telescopes
450	submillimeter	Submillimeter telescopes

Commonly used sub-divisions are

Division Name	Abbreviation	Wavelength	Characteristics
Near-infrared	NIR, IR-A DIN	0.75-1.4 µm	Defined by the water absorption, and commonly used in fiber optic telecommunication because of low attenuation losses in the SiO₂ glass (silica) medium. Image intensifiers are sensitive to this area of the spectrum. Examples include night vision devices such as night vision goggles.
Short-wavelength infrared	SWIR, IR-B DIN	1.4-3 µm	Water absorption increases significantly at 1,450 nm. The 1,530 to 1,560 nm range is the dominant spectral region for long-distance telecommunications.
Mid-wavelength infrared	MWIR, IR-C DIN. Also called intermediate infrared (IIR)	3-8 µm	In guided missile technology the 3-5 µm portion of this band is the atmospheric window in which the homing heads of passive IR 'heat seeking' missiles are designed to work, homing on to the Infrared signature of the target aircraft, typically the jet engine exhaust plume
Long-wavelength infrared	LWIR, IR-C DIN	8–15 µm	This is the "thermal imaging" region, in which sensors can obtain a completely passive picture of the outside world based on thermal emissions only and requiring no external light or thermal source such as the sun, moon or infrared illuminator. Forward-looking infrared (FLIR) systems use this area of the spectrum. This region is also called the "thermal infrared."
Far infrared	FIR	15 - 1,000 µm	(see also far-infrared laser).

Pick a representative wavelength from each band and calculate its temperature to complete the pair.

Problem 5

Terahertz radiation refers to electromagnetic waves propagating at frequencies in the terahertz range. It is synonymously termed submillimeter radiation, terahertz waves, terahertz light, T-rays, T-waves, T-light, T-lux, THz. The term typically applies to electromagnetic radiation with frequencies between high-frequency edge of the microwave band, 300 gigahertz (3 x 10¹¹ Hz),"^[55] and the long-wavelength edge of far-infrared light, 3000 GHz (3 x 10¹² Hz or 3 THz). In wavelengths, this range corresponds to 0.1 mm (or 100 µm) infrared to 1.0 mm microwave.

Microwaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz (0.3 GHz) and 300 GHz.^[56] This broad definition includes both UHF and EHF (millimeter waves), and various sources use different boundaries.^[57] In all cases, microwave includes the entire SHF band (3 to 30 GHz, or 10 to 1 cm) at minimum, with RF engineering often putting the lower boundary at 1 GHz (30 cm), and the upper around 100 GHz (3 mm).

Radio waves have frequencies from 300 Gigahertz GHz to as low as 3 Kilohertz kHz, and corresponding wavelengths from 1 millimeter to 100 kilometers.

Pick representative wavelengths from each band or sub-band and calculate a matching temperature to complete the pair.

Problem 6

The first equation at top for the problem set allows the calculation of spectral radiance. Using a simple graphics routine calculate representative spectra for each wavelength, temperature pair.

Try integrating Planck's equation at the top of the resource to give the area under any such curve. Calculate the areas under each curve you've plotted. What is this area under the curve called?

Synchrotron radiation

This problem set is aimed at synchrotron radiation.

The functional form should be sufficient to use so that synchrotron radiation is as easy to compare to spectra as is Planck's equation for blackbody radiation.

"Synchrotron radiation is the electromagnetic radiation emitted when charged particles travel in curved paths. Because in most accelerators the particle trajectories are bent by magnetic fields, synchrotron radiation is also called Magneto-Bremsstrahlung. The emitted spectrum is broadband from the microwave (harmonics of the driving RF field) to x-ray spectral regions. The radiation is vertically collimated and polarized. The synchrotron radiation output can be calculated if the electron energy, bending radius, electron current, angle relative to the orbital plane, the distance to the tangent point and vertical and horizontal acceptance angles are known."^[58]

Problem 1

Using the derivative of Planck's equation, calculate the wavelength, temperature pair for 6000 K.

The reference "Uwe" in the list near the resource page bottom calculates synchrotron radiation spectra using the electron energy (MV), the bending radius (m), the angle relative to the orbital plane (Psi/mrad), a bandwidth (%), the electron beam current (mA), starting wavelength (nm), and ending wavelength (nm) for 256 points.

Vary the electron energy at "Calculate the Synchrotron Radiation Spectrum" to get the synchrotron peak to match the (wavelength,temperature) pair.

When you have a matching synchrotron spectrum, vary the magnetic field bending radius from just above 0.0 to 2.0 and record the changes in the peak wavelength and intensity.

Problem 2

Calculate the area under the curve for the Planck spectrum with the peak at the (wavelength,temperature) pair.

For your synchrotron spectrum with its matching (wavelength,electron energy) pair, convert the electron energy to temperature to see if they match.

Adjust the electron energy until the temperatures match.

Calculate the area under the curve and compare with the area from the Planck spectrum.

If the areas do not match, adjust the bending radius to optimize the area under the curve so that only a simple scale factor if any is needed.

If a scale factor is needed, increase or decrease the electron current.

Problem 3

For an electron energy of 700.0 MeV, adjust the bending radius until the peak in total nW again matches the (wavelength, temperature) pair.

If the bending radius is inversely proportional to the magnetic field, how much stronger does the magnetic field have to be?

Problem 4

Using the electron energy that matches the temperature, adjust the bending radius until the nW peak is again at the correct wavelength.

Problem 5

When the angle relative to the orbital plane is increased in small units from zero, what changes to the bending radius must be performed to keep the peak at the same wavelength?

Document some examples.

Radiation dosages

Various types of radiation including ionizing radiation may cause harm to people, researchers, and students under different situations.

This problem set is designed to help you calculate how much radiation and of what type you may be exposed to and how much damage it might cause.

The idea is forewarned is forearmed so that should you find yourself performing research requiring the use of radiation you will use proper and effective precaution.

Dosage and damage calculations for various types of subatomic particles.

Radiation sickness

Def. any "illness produced by ionizing radiation with symptoms ranging from nausea through to death"^[59] is called radiation sickness.

Dosages

Def. an "addition of a small measured amount of a substance to something"^[60] is called a dosage.

Def. a "quantity of an agent (not always active) substance or radiation administered at any one time"^[61] is called a dose.

Dose equivalents

The equivalent dose to a tissue is found by multiplying the absorbed dose, in gray, by a weighting factor (W_R). The relation between absorbed dose D and equivalent dose H is thus:

H=W_{R}\cdot D

.

The weighting factor (sometimes referred to as a quality factor) is determined by the radiation type and energy range.^[62]

H_{T}=\sum _{R}W_{R}\cdot D_{T,R}\ ,

where

H_T is the equivalent dose absorbed by tissue T

D_T,R is the absorbed dose in tissue T by radiation type R

W_R is the weighting factor defined by the following table

Radiation type and energy		W_R
electrons, muons, photons (all energies)		1
protons and charged pions		2
alpha particles, fission fragments, heavy ions		20
neutrons (function of linear energy transfer L in keV/μm)	L < 10	1
	10 ≤ L ≤ 100	0.32·L − 2.2
	L > 100	300 / sqrt(L)

Thus for example, an absorbed dose of 1 Gy by alpha particles will lead to an equivalent dose of 20 Sv. The maximum weight of 30 is obtained for neutrons with L = 100 keV/μm.

Effective doses

“The effective dose of radiation (E), absorbed by a person is obtained by averaging over all irradiated tissues with weighting factors adding up to 1:^[62]^[63]

E=\sum _{T}W_{T}\cdot H_{T}=\sum _{T}W_{T}\sum _{R}W_{R}\cdot D_{T,R}

.

Tissue type	W_T (each)	W_T (group)
Bone marrow, colon, lung, stomach, breast, remaining tissues	0.12	0.72
Gonads	0.08	0.08
Bladder, oesophagus, liver, thyroid	0.04	0.16
Bone surface, brain, salivary glands, skin	0.01	0.04
total		1.00.

Grays

The gray (symbol: Gy) is the SI derived unit of absorbed radiation dose of ionizing radiation (for example, X-rays), and is defined as the absorption of one joule of ionizing radiation by one kilogram of matter (usually human tissue).^[64] ... [T]he rad [is] equivalent to 0.01 Gy ...

One gray is the absorption of one joule of energy, in the form of ionizing radiation, per kilogram of matter.

1\ \mathrm {Gy} =1\ {\frac {\mathrm {J} }{\mathrm {kg} }}=1\ \mathrm {m} ^{2}\cdot \mathrm {s} ^{-2}

For X rays and gamma rays, these are the same units as the sievert (Sv). For alpha particles one sievert is twenty gray. To avoid any risk of confusion between the absorbed dose (by matter) and the equivalent dose (by biological tissues), one must use the corresponding special units, gray is used instead of the joule per kilogram for absorbed dose and the sievert instead of the joule per kilogram for the dose equivalent. The word "gray" is both the singular and plural spelling.

Backgrounds

Def. "ionizing radiation that is naturally present in the environment"^[65] is called background radiation.

Background radiation is the ubiquitous ionizing radiation that the general population is exposed to, including natural and artificial sources. Both natural and artificial background radiation varies by location.

The worldwide average natural [effective radiation] dose to humans is about 2.4 millisievert (mSv) per year.^[66]

The biggest source of natural background radiation is airborne radon, a radioactive gas that emanates from the ground. Radon and its isotopes, parent radionuclides, and decay products all contribute to an average inhaled dose of 1.26 mSv/a. Radon is unevenly distributed and variable with weather, such that much higher doses apply to many areas of the world, where it represents a significant health hazard. Concentrations over 500 times higher than the world average have been found inside buildings in Scandinavia, the United States, Iran, and the Czech Republic.^[67]

Terrestrial radiation usually only includes sources that remain external to the body. The major radionuclides of concern are potassium, uranium and thorium and their decay products, some of which, like radium and radon are intensely radioactive but occur in low concentrations.

An average human contains about 30 milligrams of potassium-40 (⁴⁰K) and about 10 nanograms (10⁻⁸ g) of carbon-14 (¹⁴C), which has a decay half-life of 5,730 years. Excluding internal contamination by external radioactive material, the largest component of internal radiation exposure from biologically functional components of the human body is from potassium-40. The decay of about 4,000 nuclei of ⁴⁰K per second^[68] makes potassium the largest source of radiation in terms of number of decaying atoms. The energy of beta particles produced by ⁴⁰K is also about 10 times more powerful than the beta particles from ¹⁴C decay. ¹⁴C is present in the human body at a level of 3700 Bq with a biological half-life of 40 days.^[69] There are about 1,200 beta particles per second produced by the decay of ¹⁴C. However, a ¹⁴C atom is in the genetic information of about half the cells, while potassium is not a component of DNA. The decay of a ¹⁴C atom inside DNA in one person happens about 50 times per second, changing a carbon atom to one of nitrogen.^[70] The global average internal dose from radionuclides other than radon and its decay products is 0.29 mSv/a, of which 0.17 mSv/a comes from ⁴⁰K, 0.12 mSv/a comes from the uranium and thorium series, and 12 μSv/a comes from ¹⁴C.^[66]

Background radiation may simply be any radiation that is pervasive, whether ionizing or not. A particular example of this is the cosmic microwave background radiation, a nearly uniform glow that fills the sky in the microwave part of the spectrum; stars, galaxies and other objects of interest in radio astronomy stand out against this background.

In a laboratory, background radiation refers to the measured value from any sources that affect an instrument when a radiation source sample is not being measured. This background rate, which must be established as a stable value by multiple measurements, usually before and after sample measurement, is subtracted from the rate measured when the sample is being measured.

Problem 1

A gamma-ray burst has occurred somewhere nearby to Earth. The burst at maximum intensity lasted 100 s. While gamma-rays are absorbed by the Earth's atmosphere, conditions are such that where you are walking outside, you receive and absorb 10 % of the intensity over the 100 s.

The gamma-rays are at 1.8 MeV to the ground. The flux upon you is 4 x 10³ photons · cm^-2 · s^-1 · MeV^-1.

What is your absorbed dose and your dose equivalent? Calculate your various effective doses and your dose rate.

Using the table below, describe your likely symptoms if any.

Phase	Symptom	Whole-body absorbed dose ([Gray] Gy)
Phase	Symptom	1–2 Gy	2–6 Gy	6–8 Gy	8–30 Gy	Greater Than 30 Gy
Immediate	Nausea and vomiting	5–50%	50–100%	75–100%	90–100%	100%
	Time of onset	2–6 h	1–2 h	10–60 min	< 10 min	Minutes
	Duration	< 24 h	24–48 h	< 48 h	< 48 h	N/A (patients die in < 48 h)
	Diarrhea	None	None to mild (< 10%)	Heavy (> 10%)	Heavy (> 95%)	Heavy (100%)
	Time of onset	—	3–8 h	1–3 h	< 1 h	< 1 h
	Headache	Slight	Mild to moderate (50%)	Moderate (80%)	Severe (80–90%)	Severe (100%)
	Time of onset	—	4–24 h	3–4 h	1–2 h	< 1 h
	Fever	None	Moderate increase (10-100%)	Moderate to severe (100%)	Severe (100%)	Severe (100%)
	Time of onset	—	1–3 h	< 1 h	< 1 h	< 1 h
	[Central nervous system] CNS function	No impairment	Cognitive impairment 6–20 h	Cognitive impairment > 24 h	Rapid incapacitation	Seizures, Tremor, Ataxia, Lethargy
Latent period		28–31 days	7–28 days	< 7 days	none	none
Illness		Mild to moderate Leukopenia Fatigue Weakness	Moderate to severe Leukopenia Purpura Hemorrhage Infections Epilation after 3 Gy	Severe leukopenia High fever Diarrhea Vomiting Dizziness and disorientation Hypotension Electrolyte disturbance	Nausea Vomiting Severe diarrhea High fever Electrolyte disturbance Shock	N/A (patients die in < 48h)
Mortality	Without care	0–5%	5–100%	95–100%	100%	100%
	With care	0–5%	5–50%	50–100%	100%	100%
	Death	6–8 weeks	4–6 weeks	2–4 weeks	2 days–2 weeks	1–2 days
Source:^[71]

A few minutes after you've calculated your condition, a special report comes through an emergency channel on your cell phone to tell you that the initial report mentioned above was in error. The actual flux received whole body is 10⁶ higher. Recalculate your situation and answer the above questions and calculations again. How are you doing? Will you live to get to Problem 2?

Problem 2

Gamma-ray bursts are often followed by an X-ray afterglow. Even though you are at high altitude for some skiing when the gamma-ray burst occurred, there is probably more than enough atmosphere to prevent any further damage from the X-rays. The afterglow lasts for two days at only 5 % of the final flux of gamma rays at 120 keV. If the atmosphere had not been there, answer the questions and calculations of Problem 1 for the X-rays.

Problem 3

This just isn't your day. On a separate military channel given to you by one of your Army buddies you find out that during the gamma ray burst about the same flux of protons and pions was received by you. Recalculate again and assess your condition. Do you need to know where the nearest hospital is?

Problem 4

Oh, yes, this just keeps getting better and better. One of the people in your skiing group has a contact at the local hospital. She has just learned that alpha particles at a comparable flux were included behind the gamma-ray burst for a day and a half. Re-assess your situation again. Will you live long enough to try that new restaurant in town?

Problem 5

A first aid worker was wearing a neutron detector and happen to fall ill near you. You glance at the detector and notice it has maxed out at L = 100 keV/µm. Before any of your fingers fall off you reassess your situation one last time. Are you still going to live?

Star jumping

This astronomy problem set is a bit of a fantasy wrapped into a reality. The speed of an object such as a space ship carrying you is calculated using applied acceleration.

A simple calculation is v = v₀ + a*t. Here a speed with a specific direction (called a velocity, v) is calculated by applying an acceleration for a specific amount of time (t).

Generally, you probably won't survive accelerations above a couple of g's.

Your ship is in orbit above the Earth and your shuttle has just uploaded you into your ship.

As an endorser of the limits of the speed of light you know it would take you at least 4.1 years to get to Proxima Centauri at just under the speed of light.

Connect the stars using NASA angle of separation and stellar distances from trigonometric parallax measurements with a finite jump fuel level.

Problem 1

The Earth's standard acceleration due to gravity is g = 9.80665 m/s². Using right ascension and declination, locate Proxima Centauri.

Your ship is now moving toward Proxima Centauri at 100 m/h. Your ship has sub-relativistic drive up to about 50% c. Begin applying a two g acceleration. How much time will it take your ship to reach 0.5 c? How close to Proxima Centauri are you?

If you are less than half way there you may want to cut in your field accelerator. This device converts the local electromagnetic environment into an acceleration inside a chamber much like a rocket engine.

The difference is that this engine's accelerational capability is subject to local fluctuations in the electromagnetic environment. Once you initiate it, you may continue to accelerate as before. It is fundamentally speed of light independent. What is the maximum speed your ship and you can reach before you need to start slowing down for your arrival at Proxima Centauri?

At sub-relativistic speeds your ship consumes nuclear fuel at the rate of 1 liter per one day application of this accelerating engine.

At above 50% c, your electromagnetic accelerating engine consumes about twice as much nuclear fuel equivalents.

Fuel sources can be obtained near stars by absorbing as much low atomic number gas as possible or by consuming through fission elements above iron.

Each liter of hydrogen gas absorbed is equivalent to your current fuel consumption. But, one gram of fissionable elements yields a year's supply of fuel.

How much fuel will your journey to Proxima Centauri consume?

Elements lower in atomic number than iron are consumed in the fusion process. These are approximately consumed as indicated for hydrogen.

Although I aimed your ship toward Proxima Centauri, now that you are there and know how your fuel is consumed you can return to Earth orbit if you wish and pick your own direction to proceed in.

Or, if you like Proxima Centauri you can finish taking on fuel and pick your next location.

Problem 2

File:Aladin2014.04.25-00-43-54.611.png

This is a diagram of the astronomical sources within 20 arc minutes of Proxima Centauri. Credit: Aladin at SIMBAD.

The round trip to Proxima Centauri at about 4.1 lyrs is a good estimate of the total fuels capacity of your vessel. If you dare to go elsewhere either from Earth orbit or from Proxima Centauri, you now know your various fuel consumption rates for sub-luminal, near-luminal, and super-luminal travel.

Refueling at Proxima Centauri depends on its neighborhood similarity to that of the Earth's regarding the Sun. Proxima Centauri has more of a proto-planetary disc so you may be able to refuel in 25 % of the time it would take to cruise around the solar system if no hominin bases were present.

Your next destination depends on the availability of local or on-the-way fuel sources and how far it is.

HD 126793 is at RA 14 30 12.65686 Dec -62 51 44.4650 and 176 lyrs from Earth, based on its trigonometric parallax. Can you find a way to travel to it?

How long would the trip take? How many times would you need to refuel?

If you could bring along reserve tanks where 1 % must be used to tow and each contains 100 times as much fuel as your ship similarly distributed in type, would one or two be enough?

If your ship can absorb from the ISM as you travel, how much additional fuel will this provide based on its column density?

At the right is a diagram of the astronomical sources within 20 arc minutes of Proxima Centauri (at the center). HD 126793 is almost due South and has an arrow leading out from it. The various symbols are circle with an arrow (a star), red square (a nebular, PN or SNR), red plus (HII region), red diamond (IR object), * (UV object), X (X-ray object), and Dk Neb is a dark nebula.

Problem 3

One major limitation of your ship is its limit on acceleration due to you and any of your friends inside. The inhabited planet around HD 126793 has a novel charge monitoring device that could be fitted into your ship. Its benefit is that for one field accelerator unit per 5 c units it can pull on all your internal and suit charge units so that you and each of your friends can accelerate with your ship without harm up to ten accelerations before needing to be recharged.

Do you want one?

If you can trade for one on the planet around HD 126793 with four fissionable units of such fuel, how much faster can you go returning to Earth orbit?

How much less time would the return trip take?

What is the maximum velocity you can attain considering that you can decelerate comparably?

Problem 4

You probably noticed in your trip to the star of your choice or from your knowledge of the ISM gained in this course that the ISM between any two stars is not empty. Depending on what's out there, your ship may need some kind of protection from radiation.

At the maximum speed you attained in problem 3, mass may be considered to calculate energy independent of relative speed. If your ship as presently configured can only withstand the equivalent of a kiloton of TNT, had you hit anything, would you have survived?

Vega is about 25 lyrs from Earth. A planet there in orbit may allow you to trade for a kind of deflector that will protect you up to speeds of 100 c for objects below 1 kg. Would this be worth several fissionable fuel units?

Problem 5

Problem 4 brought up a matter of great importance: the possible presence of ship-damaging particles between destinations.

While a good shielding system is clearly necessary, what about a forward looking sensory system?

When traveling at 100 c, regular radiation transceivers may not work. In addition to communication with home, how do you detect larger particles or denser particles?

Tachyonic radar may be a reasonable idea. Tachyonic infrared, X-ray, ultraviolet, and microwaves may work as well.

This technology is not available on Earth. Are there possible superluminal sources nearby that you can reach with your ship's current configuration? Perhaps an inhabited planet near such sources would be willing to trade such a detection or communication system.

From superluminal astronomy and your current location, find three to five nearby stars along the approximate line of sight to one of these superluminal sources or another you may have found. Plot an exploratory course to at least one.

Is your ship's present status sufficient to undertake such an exploration?

Lenses and focal lengths

Massless units

In addition to the energy phantoms, construct each physical unit without mass or charge and evaluate some problems where these have been used.

Superluminal problems

This problem set focuses on superluminal phenomena with an emphasis on optical illusions.

Hypotheses

Construction of a set of problems can induce students to learn how to solve all the problems in the set.

References

↑ Tohru (30 December 2005). energy. San Francisco, California: Wikimedia Foundation, Inc. http://en.wiktionary.org/wiki/energy. Retrieved 2013-07-14.
↑ force. San Francisco, California: Wikimedia Foundation, Inc. September 1, 2011. https://en.wiktionary.org/wiki/force. Retrieved 2013-12-04.
↑ - Proposition 75, Theorem 35: p.956 - I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton's Principia, by I.Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 ISBN 0-520-08817-4
↑ CODATA2006. http://www.physics.nist.gov/cgi-bin/cuu/Value?bg.
↑ Table 3. Coherent derived units in the SI with special names and symbols, In: The International System of Units (SI). International Bureau of Weights and Measures. 2006. http://www.bipm.org/en/si/si_brochure/chapter2/2-2/table3.html.
↑ F. Van Leeuwen (November 1, 2007). "Validation of the new Hipparcos reduction". Astronomy & Astrophysics 474 (2): 653-64. doi:10.1051/0004-6361:20078357. http://adsabs.harvard.edu/abs/2007A%26A...474..653V. Retrieved 2013-12-05.
↑ ^7.0 ^7.1 ^7.2 P. K. Seidelmann (1976). Measuring the Universe The IAU and astronomical units. International Astronomical Union. http://www.iau.org/public/measuring/. Retrieved 2011-11-27.
↑ International Astronomical Union "SI units" accessed February 18, 2010. (See Table 5 and section 5.15.) Reprinted from George A. Wilkins & IAU Commission 5, "The IAU Style Manual (1989)" (PDF file) in IAU Transactions Vol. XXB
↑ ^9.0 ^9.1 ^9.2 ^9.3 ^9.4 ^9.5 ^9.6 chain. San Francisco, California: Wikimedia Foundation, Inc. December 17, 2013. https://en.wiktionary.org/wiki/chain. Retrieved 2013-12-25.
↑ fortnight. San Francisco, California: Wikimedia Foundation, Inc. November 27, 2013. https://en.wiktionary.org/wiki/fortnight. Retrieved 2013-12-25.
↑ furlong. San Francisco, California: Wikimedia Foundation, Inc. December 10, 2013. https://en.wiktionary.org/wiki/furlong. Retrieved 2013-12-25.
↑ ^12.0 ^12.1 furrow. San Francisco, California: Wikimedia Foundation, Inc. December 10, 2013. https://en.wiktionary.org/wiki/furrow. Retrieved 2013-12-25.
↑ league. San Francisco, California: Wikimedia Foundation, Inc. December 10, 2013. https://en.wiktionary.org/wiki/league. Retrieved 2013-12-25.
↑ sennight. San Francisco, California: Wikimedia Foundation, Inc. December 12, 2013. https://en.wiktionary.org/wiki/sennight. Retrieved 2013-12-25.
↑ ^15.0 ^15.1 ^15.2 ^15.3 week. San Francisco, California: Wikimedia Foundation, Inc. November 27, 2013. https://en.wiktionary.org/wiki/week. Retrieved 2013-12-25.
↑ Paul A. Tipler, Gene Mosca (May 1, 2007). Physics for Scientists and Engineers. Macmillan. pp. 1172. ISBN 142920124X. http://books.google.com/books?id=AttDBYgLeZkC&pg=PA614&lpg=PA614&source=bl&ots=mDyTt5SY03&sig=-IdefwfOk591NKKnKm2iPsorRxo&hl=en&sa=X&ei=XkPGUs6UCdDqkAeeuYF4&ved=0CDAQ6AEwBA. Retrieved 2014-01-02.
↑ I. Dzyaloshinskii (May 1992). "Effects of the finite proton mass in a hydrogen atom in crossed magnetic and electric fields: a state with a giant electric dipole moment". Physics Letters A 165 (1): 69-71. doi:10.1016/0375-9601(92)91056-W. http://www.sciencedirect.com/science/article/pii/037596019291056W. Retrieved 2014-02-13.
↑ acre. San Francisco, California: Wikimedia Foundation, Inc. January 23, 2014. https://en.wiktionary.org/wiki/acre. Retrieved 2014-01-23.
↑ acre-foot. San Francisco, California: Wikimedia Foundation, Inc. November 9, 2012. https://en.wiktionary.org/wiki/acre-foot. Retrieved 2014-01-23.
↑ magnetomotive-force. San Francisco, California: Wikimedia Foundation, Inc. June 19, 2013. https://en.wiktionary.org/wiki/magnetomotive_force. Retrieved 2014-01-23.
↑ ampere-turn. San Francisco, California: Wikimedia Foundation, Inc. August 24, 2012. https://en.wiktionary.org/wiki/ampere-turn. Retrieved 2014-01-23.
↑ API gravity. San Francisco, California: Wikimedia Foundation, Inc. June 16, 2013. https://en.wiktionary.org/wiki/API_gravity. Retrieved 2014-01-23.
↑ arshin. San Francisco, California: Wikimedia Foundation, Inc. October 9, 2013. https://en.wiktionary.org/wiki/arshin. Retrieved 2014-01-23.
↑ Russ Rowlett (September 1, 2004). Units: S, In: How Many? A Dictionary of Units of Measurement. University of North Carolina at Chapel Hill. http://www.unc.edu/~rowlett/units/dictS.html. Retrieved 2009-12-14.
↑ Jonathon Green (December 1987). Dictionary of Jargon. Routledge Kegan & Paul. p. 487. ISBN 0-7100-9919-3. http://books.google.com/?id=P0QOAAAAQAAJ&pg=PA487. Retrieved 2009-12-14.
↑ flux. San Francisco, California: Wikimedia Foundation, Inc. January 24, 2014. https://en.wiktionary.org/wiki/flux. Retrieved 2014-01-25.
↑ millibar. San Francisco, California: Wikimedia Foundation, Inc. October 6, 2013. https://en.wiktionary.org/wiki/millibar. Retrieved 2014-02-13.
↑ knot. San Francisco, California: Wikimedia Foundation, Inc. February 1, 2014. https://en.wiktionary.org/wiki/knot. Retrieved 2014-02-13.
↑ nautical mile. San Francisco, California: Wikimedia Foundation, Inc. December 11, 2013. https://en.wiktionary.org/wiki/nautical_mile. Retrieved 2014-02-13.
↑ ^30.0 ^30.1 voltage. San Francisco, California: Wikimedia Foundation, Inc. January 25, 2014. https://en.wiktionary.org/wiki/voltage. Retrieved 2014-03-05.
↑ ^31.0 ^31.1 current. San Francisco, California: Wikimedia Foundation, Inc. January 10, 2014. https://en.wiktionary.org/wiki/current. Retrieved 2014-02-13.
↑ electrical resistance. San Francisco, California: Wikimedia Foundation, Inc. October 7, 2013. https://en.wiktionary.org/wiki/electrical_resistance. Retrieved 2014-02-13.
↑ Smith, Warren Modern Lens Design 2005 McGraw-Hill
↑ ^34.0 ^34.1 Smith, Warren Modern Optical Engineering, 4th Ed. 2007 McGraw-Hill Professional
↑ Sidney F. Ray (2000). "Camera Features". In Ralph Eric Jacobson. Manual of Photography: A Textbook of Photographic and Digital Imaging (Ninth ed.). Focal Press. pp. 131–2. ISBN 0-240-51574-9. http://books.google.com/books?id=HHX4xB94vcMC&pg=PA132&ots=7Gq_Az_-zl&sig=bQ5bvKIS-y1_Q4km6Pm-yCZDcGo.
↑ Cub Kahn (1999). Essential Skills for Nature Photography. Amherst Media. ISBN 1-58428-009-3. http://books.google.com/books?id=EZhNY--TZjIC&pg=PT21&ei=h0MHSejTFI_gswOh3eDzDQ.
↑ mass. San Francisco, California: Wikimedia Foundation, Inc. February 20, 2014. https://en.wiktionary.org/wiki/mass. Retrieved 2014-02-28.
↑ inertia. San Francisco, California: Wikimedia Foundation, Inc. February 20, 2014. https://en.wiktionary.org/wiki/inertia. Retrieved 2014-02-28.
↑ Isaac Newton, The Principia, A new translation by I.B. Cohen and A. Whitman, University of California press, Berkeley 1999.
↑ momentum. San Francisco, California: Wikimedia Foundation, Inc. January 30, 2014. https://en.wiktionary.org/wiki/momentum. Retrieved 2014-02-28.
↑ angular momentum. San Francisco, California: Wikimedia Foundation, Inc. October 9, 2013. https://en.wiktionary.org/wiki/angular_momentum. Retrieved 2014-02-28.
↑ torque. San Francisco, California: Wikimedia Foundation, Inc. January 10, 2014. https://en.wiktionary.org/wiki/torque. Retrieved 2014-02-28.
↑ ^43.0 ^43.1 moment of force. San Francisco, California: Wikimedia Foundation, Inc. December 10, 2013. https://en.wiktionary.org/wiki/moment_of_force. Retrieved 2014-02-28.
↑ foot-pound. San Francisco, California: Wikimedia Foundation, Inc. June 20, 2013. https://en.wiktionary.org/wiki/foot-pound. Retrieved 2014-02-28.
↑ Russell C. Hibbeler (2009). Engineering Mechanics. Upper Saddle River, New Jersey: Pearson Prentice Hall. pp. 314, 153. ISBN 978-0-13-607791-6. http://books.google.com/?id=tOFRjXB-XvMC&pg=PA314.
↑ circuit. San Francisco, California: Wikimedia Foundation, Inc. January 27, 2014. https://en.wiktionary.org/wiki/circuit. Retrieved 2014-03-05.
↑ ampere. San Francisco, California: Wikimedia Foundation, Inc. February 9, 2014. https://en.wiktionary.org/wiki/ampere. Retrieved 2014-03-05.
↑ Jamie Bock (February 16, 2011). Herschel's View of 'Lockman Hole'. Pasadena, California USA: Caltech. http://www.herschel.caltech.edu/image/nhsc2011-003a. Retrieved 2014-03-15.
↑ ^49.0 ^49.1 column density. San Francisco, California: Wikimedia Foundation, Inc. November 10, 2012. https://en.wiktionary.org/wiki/column_density. Retrieved 2014-03-15.
↑ ^50.0 ^50.1 Felix J. Lockman and Keith Jahoda and Dan McCammon (March 1, 1986). "The structure of galactic HI in directions of low total column density". The Astrophysical Journal 302 (03): 432-49. doi:10.1086/164002. http://adsabs.harvard.edu/abs/1986ApJ...302..432L. Retrieved 2014-03-15.
↑ ^51.0 ^51.1 David J. Schlegel and Douglas P. Finkbeiner and Marc Davis (June 20 1998). "Maps of Dust Infrared Emission for Use in Estimation of Reddening and Cosmic Microwave Background Radiation Foregrounds". The Astrophysical Journal 500 (2): 525-53. http://iopscience.iop.org/0004-637X/500/2/525/fulltext/. Retrieved 2014-03-15.
↑ spectrograph. San Francisco, California: Wikimedia Foundation, Inc. October 8, 2013. https://en.wiktionary.org/wiki/spectrograph. Retrieved 2014-03-24.
↑ spectrogram. San Francisco, California: Wikimedia Foundation, Inc. June 19, 2013. https://en.wiktionary.org/wiki/spectrogram. Retrieved 2014-03-24.
↑ IPAC Staff. Near, Mid and Far-Infrared. NASA ipac. http://www.ipac.caltech.edu/Outreach/Edu/Regions/irregions.html. Retrieved 2007-04-04.
↑ Hankwang (October 31, 2008). Terahertz radiation: Difference between revisions. http://en.wikipedia.org/w/index.php?title=Terahertz_radiation&diff=248835142&oldid=248831987. Retrieved 2012-08-05.
↑ Pozar, David M. (1993). Microwave Engineering Addison-Wesley Publishing Company. ISBN 0-201-50418-9.
↑ http://www.google.com/search?hl=en&defl=en&q=define:microwave&ei=e6CMSsWUI5OHmQee2si1DQ&sa=X&oi=glossary_definition&ct=title
↑ Uwe Arp (June 2003). Synchrotron Radiation. Gaithersburg, Maryland USA: National Institute of Standards and Technology NIST). http://physics.nist.gov/MajResFac/SURF/SURF/sr.html. Retrieved 2014-04-02.
↑ radiation sickness. San Francisco, California: Wikimedia Foundation, Inc. January 10, 2014. https://en.wiktionary.org/wiki/radiation_sickness. Retrieved 2014-04-10.
↑ dosage. San Francisco, California: Wikimedia Foundation, Inc. February 9, 2014. https://en.wiktionary.org/wiki/dosage. Retrieved 2014-04-10.
↑ dose. San Francisco, California: Wikimedia Foundation, Inc. March 27, 2014. https://en.wiktionary.org/wiki/dose. Retrieved 2014-04-10.
↑ ^62.0 ^62.1 The 2007 Recommendations. International Commission on Radiological Protection. http://www.icrp.org/docs/ICRP_Publication_103-Annals_of_the_ICRP_37(2-4)-Free_extract.pdf. Retrieved 2011-04-15.
↑ A D Wrixon. New ICRP recommendations. Journal on Radiological Protection. http://iopscience.iop.org/0952-4746/28/2/R02/pdf/0952-4746_28_2_R02.pdf. Retrieved 2011-04-15.
↑ The International System of Units (SI). Bureau International des Poids et Mesures (BIPM). http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf. Retrieved 2010-01-31.
↑ background radiation. San Francisco, California: Wikimedia Foundation, Inc. October 6, 2013. https://en.wiktionary.org/wiki/background_radiation. Retrieved 2014-04-10.
↑ ^66.0 ^66.1 United Nations Scientific Committee on the Effects of Atomic Radiation. Sources and effects of ionizing radiation 2008 (published 2010). New York: United Nations. p. 4. ISBN 978-92-1-142274-0. http://www.unscear.org/unscear/en/publications/2008_1.html. Retrieved 9 November 2012.
↑ United Nations Scientific Committee on the Effects of Atomic Radiation. "Annex E: Sources-to-effects assessment for radon in homes and workplaces". Effects of Ionizing Radiation 2006 (published 2008). II. New York: United Nations. ISBN 978-92-1-142263-4. http://www.unscear.org/docs/reports/2006/09-81160_Report_Annex_E_2006_Web.pdf. Retrieved 2 December 2012.
↑ S. C. Diroff (April 2011). Radioactive human body — Harvard University Natural Science Lecture Demonstrations. http://www.fas.harvard.edu/~scdiroff/lds/QuantumRelativity/RadioactiveHumanBody/RadioactiveHumanBody.html.
↑ http://www.ead.anl.gov/pub/doc/carbon14.pdf
↑ Isaac Asimov. "The Explosions Within Us". Only A Trillion (Revised and updated 1976 ed.). New York: ACE books. pp. 37–9. ISBN 1-157-09468-6.
↑ Radiation Exposure and Contamination. http://www.merckmanuals.com/professional/injuries_poisoning/radiation_exposure_and_contamination/radiation_exposure_and_contamination.html. Retrieved 2 June 2013.

External links

[EnergyWikt-1] Tohru (30 December 2005). energy. San Francisco, California: Wikimedia Foundation, Inc. http://en.wiktionary.org/wiki/energy. Retrieved 2013-07-14.

[ForceWikt-2] force. San Francisco, California: Wikimedia Foundation, Inc. September 1, 2011. https://en.wiktionary.org/wiki/force. Retrieved 2013-12-04.

[Newton1-3] - Proposition 75, Theorem 35: p.956 - I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton's Principia, by I.Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 ISBN 0-520-08817-4

[NISTgravity-4] CODATA2006. http://www.physics.nist.gov/cgi-bin/cuu/Value?bg.

[IBWM-5] Table 3. Coherent derived units in the SI with special names and symbols, In: The International System of Units (SI). International Bureau of Weights and Measures. 2006. http://www.bipm.org/en/si/si_brochure/chapter2/2-2/table3.html.

[Leeuwen-6] F. Van Leeuwen (November 1, 2007). "Validation of the new Hipparcos reduction". Astronomy & Astrophysics 474 (2): 653-64. doi:10.1051/0004-6361:20078357. http://adsabs.harvard.edu/abs/2007A%26A...474..653V. Retrieved 2013-12-05.

[Seidelmann-7] 7.0 ^7.1 ^7.2 P. K. Seidelmann (1976). Measuring the Universe The IAU and astronomical units. International Astronomical Union. http://www.iau.org/public/measuring/. Retrieved 2011-11-27.

[Wilkins-8] International Astronomical Union "SI units" accessed February 18, 2010. (See Table 5 and section 5.15.) Reprinted from George A. Wilkins & IAU Commission 5, "The IAU Style Manual (1989)" (PDF file) in IAU Transactions Vol. XXB

[ChainWikt-9] 9.0 ^9.1 ^9.2 ^9.3 ^9.4 ^9.5 ^9.6 chain. San Francisco, California: Wikimedia Foundation, Inc. December 17, 2013. https://en.wiktionary.org/wiki/chain. Retrieved 2013-12-25.

[FortnightWikt-10] fortnight. San Francisco, California: Wikimedia Foundation, Inc. November 27, 2013. https://en.wiktionary.org/wiki/fortnight. Retrieved 2013-12-25.

[FurlongWikt-11] furlong. San Francisco, California: Wikimedia Foundation, Inc. December 10, 2013. https://en.wiktionary.org/wiki/furlong. Retrieved 2013-12-25.

[FurrowWikt-12] 12.0 ^12.1 furrow. San Francisco, California: Wikimedia Foundation, Inc. December 10, 2013. https://en.wiktionary.org/wiki/furrow. Retrieved 2013-12-25.

[LeagueWikt-13] league. San Francisco, California: Wikimedia Foundation, Inc. December 10, 2013. https://en.wiktionary.org/wiki/league. Retrieved 2013-12-25.

[SennightWikt-14] sennight. San Francisco, California: Wikimedia Foundation, Inc. December 12, 2013. https://en.wiktionary.org/wiki/sennight. Retrieved 2013-12-25.

[WeekWikt-15] 15.0 ^15.1 ^15.2 ^15.3 week. San Francisco, California: Wikimedia Foundation, Inc. November 27, 2013. https://en.wiktionary.org/wiki/week. Retrieved 2013-12-25.

[Tipler-16] Paul A. Tipler, Gene Mosca (May 1, 2007). Physics for Scientists and Engineers. Macmillan. pp. 1172. ISBN 142920124X. http://books.google.com/books?id=AttDBYgLeZkC&pg=PA614&lpg=PA614&source=bl&ots=mDyTt5SY03&sig=-IdefwfOk591NKKnKm2iPsorRxo&hl=en&sa=X&ei=XkPGUs6UCdDqkAeeuYF4&ved=0CDAQ6AEwBA. Retrieved 2014-01-02.

[Dzyaloshinskii-17] I. Dzyaloshinskii (May 1992). "Effects of the finite proton mass in a hydrogen atom in crossed magnetic and electric fields: a state with a giant electric dipole moment". Physics Letters A 165 (1): 69-71. doi:10.1016/0375-9601(92)91056-W. http://www.sciencedirect.com/science/article/pii/037596019291056W. Retrieved 2014-02-13.

[AcreWikt-18] acre. San Francisco, California: Wikimedia Foundation, Inc. January 23, 2014. https://en.wiktionary.org/wiki/acre. Retrieved 2014-01-23.

[AcreFootWikt-19] acre-foot. San Francisco, California: Wikimedia Foundation, Inc. November 9, 2012. https://en.wiktionary.org/wiki/acre-foot. Retrieved 2014-01-23.

[MagnetomotiveForceWikt-20] magnetomotive-force. San Francisco, California: Wikimedia Foundation, Inc. June 19, 2013. https://en.wiktionary.org/wiki/magnetomotive_force. Retrieved 2014-01-23.

[AmpereTurnWikt-21] ampere-turn. San Francisco, California: Wikimedia Foundation, Inc. August 24, 2012. https://en.wiktionary.org/wiki/ampere-turn. Retrieved 2014-01-23.

[APIGravityWikt-22] API gravity. San Francisco, California: Wikimedia Foundation, Inc. June 16, 2013. https://en.wiktionary.org/wiki/API_gravity. Retrieved 2014-01-23.

[ArshinWikt-23] arshin. San Francisco, California: Wikimedia Foundation, Inc. October 9, 2013. https://en.wiktionary.org/wiki/arshin. Retrieved 2014-01-23.

[Rowlett-24] Russ Rowlett (September 1, 2004). Units: S, In: How Many? A Dictionary of Units of Measurement. University of North Carolina at Chapel Hill. http://www.unc.edu/~rowlett/units/dictS.html. Retrieved 2009-12-14.

[Green-25] Jonathon Green (December 1987). Dictionary of Jargon. Routledge Kegan & Paul. p. 487. ISBN 0-7100-9919-3. http://books.google.com/?id=P0QOAAAAQAAJ&pg=PA487. Retrieved 2009-12-14.

[FluxWikt-26] flux. San Francisco, California: Wikimedia Foundation, Inc. January 24, 2014. https://en.wiktionary.org/wiki/flux. Retrieved 2014-01-25.

[MillibarWikt-27] millibar. San Francisco, California: Wikimedia Foundation, Inc. October 6, 2013. https://en.wiktionary.org/wiki/millibar. Retrieved 2014-02-13.

[KnotWikt-28] knot. San Francisco, California: Wikimedia Foundation, Inc. February 1, 2014. https://en.wiktionary.org/wiki/knot. Retrieved 2014-02-13.

[NauticalMileWikt-29] nautical mile. San Francisco, California: Wikimedia Foundation, Inc. December 11, 2013. https://en.wiktionary.org/wiki/nautical_mile. Retrieved 2014-02-13.

[VoltageWikt-30] 30.0 ^30.1 voltage. San Francisco, California: Wikimedia Foundation, Inc. January 25, 2014. https://en.wiktionary.org/wiki/voltage. Retrieved 2014-03-05.

[CurrentWikt-31] 31.0 ^31.1 current. San Francisco, California: Wikimedia Foundation, Inc. January 10, 2014. https://en.wiktionary.org/wiki/current. Retrieved 2014-02-13.

[ElectricalResistanceWikt-32] electrical resistance. San Francisco, California: Wikimedia Foundation, Inc. October 7, 2013. https://en.wiktionary.org/wiki/electrical_resistance. Retrieved 2014-02-13.

[Smith2005-33] Smith, Warren Modern Lens Design 2005 McGraw-Hill

[ReferenceA-34] 34.0 ^34.1 Smith, Warren Modern Optical Engineering, 4th Ed. 2007 McGraw-Hill Professional

[ray-35] Sidney F. Ray (2000). "Camera Features". In Ralph Eric Jacobson. Manual of Photography: A Textbook of Photographic and Digital Imaging (Ninth ed.). Focal Press. pp. 131–2. ISBN 0-240-51574-9. http://books.google.com/books?id=HHX4xB94vcMC&pg=PA132&ots=7Gq_Az_-zl&sig=bQ5bvKIS-y1_Q4km6Pm-yCZDcGo.

[kahn-36] Cub Kahn (1999). Essential Skills for Nature Photography. Amherst Media. ISBN 1-58428-009-3. http://books.google.com/books?id=EZhNY--TZjIC&pg=PT21&ei=h0MHSejTFI_gswOh3eDzDQ.

[MassWikt-37] mass. San Francisco, California: Wikimedia Foundation, Inc. February 20, 2014. https://en.wiktionary.org/wiki/mass. Retrieved 2014-02-28.

[InertiaWikt-38] inertia. San Francisco, California: Wikimedia Foundation, Inc. February 20, 2014. https://en.wiktionary.org/wiki/inertia. Retrieved 2014-02-28.

[Newton-39] Isaac Newton, The Principia, A new translation by I.B. Cohen and A. Whitman, University of California press, Berkeley 1999.

[MomentumWikt-40] momentum. San Francisco, California: Wikimedia Foundation, Inc. January 30, 2014. https://en.wiktionary.org/wiki/momentum. Retrieved 2014-02-28.

[AngularMomentumWikt-41] angular momentum. San Francisco, California: Wikimedia Foundation, Inc. October 9, 2013. https://en.wiktionary.org/wiki/angular_momentum. Retrieved 2014-02-28.

[TorqueWikt-42] torque. San Francisco, California: Wikimedia Foundation, Inc. January 10, 2014. https://en.wiktionary.org/wiki/torque. Retrieved 2014-02-28.

[MomentOfForceWikt-43] 43.0 ^43.1 moment of force. San Francisco, California: Wikimedia Foundation, Inc. December 10, 2013. https://en.wiktionary.org/wiki/moment_of_force. Retrieved 2014-02-28.

[FootPoundWikt-44] foot-pound. San Francisco, California: Wikimedia Foundation, Inc. June 20, 2013. https://en.wiktionary.org/wiki/foot-pound. Retrieved 2014-02-28.

[Hibbeler-45] Russell C. Hibbeler (2009). Engineering Mechanics. Upper Saddle River, New Jersey: Pearson Prentice Hall. pp. 314, 153. ISBN 978-0-13-607791-6. http://books.google.com/?id=tOFRjXB-XvMC&pg=PA314.

[CircuitWikt-46] circuit. San Francisco, California: Wikimedia Foundation, Inc. January 27, 2014. https://en.wiktionary.org/wiki/circuit. Retrieved 2014-03-05.

[AmpereWikt-47] ampere. San Francisco, California: Wikimedia Foundation, Inc. February 9, 2014. https://en.wiktionary.org/wiki/ampere. Retrieved 2014-03-05.

[Bock2011-48] Jamie Bock (February 16, 2011). Herschel's View of 'Lockman Hole'. Pasadena, California USA: Caltech. http://www.herschel.caltech.edu/image/nhsc2011-003a. Retrieved 2014-03-15.

[ColumnDensityWikt-49] 49.0 ^49.1 column density. San Francisco, California: Wikimedia Foundation, Inc. November 10, 2012. https://en.wiktionary.org/wiki/column_density. Retrieved 2014-03-15.

[Lockman-50] 50.0 ^50.1 Felix J. Lockman and Keith Jahoda and Dan McCammon (March 1, 1986). "The structure of galactic HI in directions of low total column density". The Astrophysical Journal 302 (03): 432-49. doi:10.1086/164002. http://adsabs.harvard.edu/abs/1986ApJ...302..432L. Retrieved 2014-03-15.

[Schlegel-51] 51.0 ^51.1 David J. Schlegel and Douglas P. Finkbeiner and Marc Davis (June 20 1998). "Maps of Dust Infrared Emission for Use in Estimation of Reddening and Cosmic Microwave Background Radiation Foregrounds". The Astrophysical Journal 500 (2): 525-53. http://iopscience.iop.org/0004-637X/500/2/525/fulltext/. Retrieved 2014-03-15.

[SpectrographWikt-52] spectrograph. San Francisco, California: Wikimedia Foundation, Inc. October 8, 2013. https://en.wiktionary.org/wiki/spectrograph. Retrieved 2014-03-24.

[SpectrogramWikt-53] spectrogram. San Francisco, California: Wikimedia Foundation, Inc. June 19, 2013. https://en.wiktionary.org/wiki/spectrogram. Retrieved 2014-03-24.

[IPAC-54] IPAC Staff. Near, Mid and Far-Infrared. NASA ipac. http://www.ipac.caltech.edu/Outreach/Edu/Regions/irregions.html. Retrieved 2007-04-04.

[Hankwang-55] Hankwang (October 31, 2008). Terahertz radiation: Difference between revisions. http://en.wikipedia.org/w/index.php?title=Terahertz_radiation&diff=248835142&oldid=248831987. Retrieved 2012-08-05.

[Pozer-56] Pozar, David M. (1993). Microwave Engineering Addison-Wesley Publishing Company. ISBN 0-201-50418-9.

[googlegloss-57] ttp://www.google.com/search?hl=en&defl=en&q=define:microwave&ei=e6CMSsWUI5OHmQee2si1DQ&sa=X&oi=glossary_definition&ct=title

[Arp-58] Uwe Arp (June 2003). Synchrotron Radiation. Gaithersburg, Maryland USA: National Institute of Standards and Technology NIST). http://physics.nist.gov/MajResFac/SURF/SURF/sr.html. Retrieved 2014-04-02.

[RadiationSicknessWikt-59] radiation sickness. San Francisco, California: Wikimedia Foundation, Inc. January 10, 2014. https://en.wiktionary.org/wiki/radiation_sickness. Retrieved 2014-04-10.

[DosageWikt-60] dosage. San Francisco, California: Wikimedia Foundation, Inc. February 9, 2014. https://en.wiktionary.org/wiki/dosage. Retrieved 2014-04-10.

[DoseWikt-61] dose. San Francisco, California: Wikimedia Foundation, Inc. March 27, 2014. https://en.wiktionary.org/wiki/dose. Retrieved 2014-04-10.

[icrp103-62] 62.0 ^62.1 The 2007 Recommendations. International Commission on Radiological Protection. http://www.icrp.org/docs/ICRP_Publication_103-Annals_of_the_ICRP_37(2-4)-Free_extract.pdf. Retrieved 2011-04-15.

[Wrixon-63] A D Wrixon. New ICRP recommendations. Journal on Radiological Protection. http://iopscience.iop.org/0952-4746/28/2/R02/pdf/0952-4746_28_2_R02.pdf. Retrieved 2011-04-15.

[bipm-64] The International System of Units (SI). Bureau International des Poids et Mesures (BIPM). http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf. Retrieved 2010-01-31.

[BackgroundRadiationWikt-65] background radiation. San Francisco, California: Wikimedia Foundation, Inc. October 6, 2013. https://en.wiktionary.org/wiki/background_radiation. Retrieved 2014-04-10.

[UNSCEAR2008-66] 66.0 ^66.1 United Nations Scientific Committee on the Effects of Atomic Radiation. Sources and effects of ionizing radiation 2008 (published 2010). New York: United Nations. p. 4. ISBN 978-92-1-142274-0. http://www.unscear.org/unscear/en/publications/2008_1.html. Retrieved 9 November 2012.

[UNSCEAR2006E-67] United Nations Scientific Committee on the Effects of Atomic Radiation. "Annex E: Sources-to-effects assessment for radon in homes and workplaces". Effects of Ionizing Radiation 2006 (published 2008). II. New York: United Nations. ISBN 978-92-1-142263-4. http://www.unscear.org/docs/reports/2006/09-81160_Report_Annex_E_2006_Web.pdf. Retrieved 2 December 2012.

[Diroff-68] S. C. Diroff (April 2011). Radioactive human body — Harvard University Natural Science Lecture Demonstrations. http://www.fas.harvard.edu/~scdiroff/lds/QuantumRelativity/RadioactiveHumanBody/RadioactiveHumanBody.html.

[69] ttp://www.ead.anl.gov/pub/doc/carbon14.pdf

[Asimov-70] Isaac Asimov. "The Explosions Within Us". Only A Trillion (Revised and updated 1976 ed.). New York: ACE books. pp. 37–9. ISBN 1-157-09468-6.

[71] Radiation Exposure and Contamination. http://www.merckmanuals.com/professional/injuries_poisoning/radiation_exposure_and_contamination/radiation_exposure_and_contamination.html. Retrieved 2 June 2013.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

	students in the India must use Greenwich mean time
	about 5 x 10⁸ years ago
	a high-powered robotic telescope was lost on the shuttle Cambrian
	a student in Xinjiang has an abacus configured to the geologic time scale
	on-site use of two high-powered telescopes is available
	trilobites tried to communicate with Earth

	the presence of oceans on the Earth
	locally available carving tools
	light pollution
	most astronomical objects are observed at night
	currently dormant volcanoes seldom erupt
	human habitation increases near an astronomical observatory

	Chandra X-ray Observatory
	Big Bear
	TRACE
	Kodaikanal
	the Hubble
	Lomnický štít
	McMath-Pierce
	SOFIA
	Rosetta

	polyhedra
	globes
	hectares
	pyramid
	pathway
	furloughs

	cosmic-ray astronomy
	infrared astronomy
	neutrino astronomy
	proton astronomy
	ultraviolet astronomy
	electron astronomy

Point added for a correct answer:
Points for an incorrect answer:
Ignore the questions' coefficients:

	TRUE
	FALSE

	TRUE
	FALSE

	TRUE
	FALSE