Chemicals/Reactions

Chemical reactions are associated with some changes in the chemical nature/properties of substances. For example, under specific circumstances, when hydrogen chemically reacts with oxygen, water is formed. The chemical propeties of water are quite different from its constituent elements, i.e. hydrogen and oxygen.
Chemical reactions can be classified into two main types: endothermic and exothermic reactions. An endothermic reaction is sustained only when the required quantity of heat is continuously supplied to the reaction zone and the reation absorbs heat. Exothermic reactions release heat and require removal of heat from the reaction zone for sustenance.
Equations
[edit | edit source]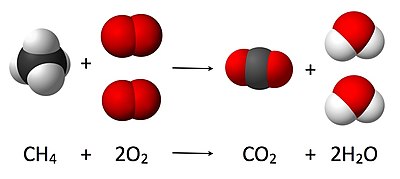
Centered above is a visual that shows how the law of conservation of atoms works: there must be the same number of atoms of each element for the reactants and the products.
Each term in the reaction equation has two parts: a coefficient indicating the number of molecules and a chemical formula for each molecule involved in the reaction.
A molecule of methane (CH4) is combined with two molecules of oxygen (O2) to produce a molecule of carbon dioxide (CO2) and two molecules of water vapor (H2O).
The physical state of the chemicals has not been included. Depending upon the conditions for which the equation records the reaction, all molecules could be gases. This may be represented as
where (g) stands for gas.
Written more generally,
Here, a = 1, A = CH4, b = 2 , B = O2, c = 1, C = CO2, d = 2, and D = H2O. Including the gaseous state of each molecule yields
The liquid methane/liquid oxygen reaction motor or engine pictured at the page top is probably preheating each right before the components enter the reaction chamber which is just above the exhaust manifold.
Thermodynamics
[edit | edit source]- .
- G: Gibbs free energy, H: enthalpy, T: temperature, S: entropy, Δ: difference (change between original and product).
At equilibrium, the Gibbs free energy is zero.
Exothermic reactions: ΔH is negative and energy is released (ΔG is negative).
Endothermic reactions: ΔS is positive, ΔT is positive, or ΔH is positive, and ΔG is positive.
- ;
ΔH° is zero at 1855 K. Above 1855 K the reaction is exothermic.
Above 1100 K the reaction is reversed.[1]
Internal energy:
- U: internal energy, S: entropy, p: pressure, μ: chemical potential, n: number of molecules, d: small differential change.
Reaction kinetics
[edit | edit source]Variables:
- reactant concentrations,
- surface area for contact between reactants,
- pressure,
- temperature,
- catalyst,
- electromagnetics, and
- activation energy (Ea).
The rate v of a reaction is given by
Integration yields
k has the dimension 1/time, [A](t) is concentration at a time t and [A]0 is the initial concentration.
The Arrhenius relation for the temperature dependence is
where kB is Boltzmann's constant.
Elementary reactions
[edit | edit source]
Def. a "reaction for which no reaction intermediates have been detected or need to be postulated in order to describe the chemical reaction on a molecular scale"[2] is called an elementary reaction.
"An elementary reaction is assumed to occur in a single step and to pass through a single transition state."[2]
The reaction at the top of this section shows trans-azobenzene being transformed into cis-azobenzene induced by light (hν) or heat (Δ). Trans means widely separated and cis means close by. The double arrow (⇌) indicates that the reaction is reversible.
Dissociation reactions
[edit | edit source]- Dissociation of a molecule AB into fragments A and B
Addition reactions
[edit | edit source]Metathesis reactions
[edit | edit source]for example,
Reaction types
[edit | edit source]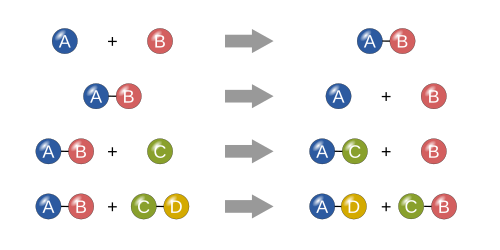
Synthesis reactions
[edit | edit source]Decomposition reactions
[edit | edit source]Single replacement reactions
[edit | edit source]- single replacement.
Double replacement reactions
[edit | edit source]- double replacement.
Oxidation and reduction
[edit | edit source]
Electron transfer reactions
[edit | edit source]
Sodium metal loses an electron to each fluorine atom so that
- by electron transfer.
Complexation
[edit | edit source]
A neutral iron (Fe) atom yields electrons to form a complex with two C5H5 ligands.
Acid-base reactions
[edit | edit source]Phosphate reactions
[edit | edit source]A phosphate reaction is a chemical reaction that leads to the transformation of one set of phosphates to another.
Def. "[a] colourless liquid, H3PO4"[3] is called phosphoric acid.
Def. "[o]rdinary phosphoric acid, H3PO4", after orthophosphoric acid, is called orthophosphoric acid.
"Orthophosphoric acid is a non-toxic, inorganic, rather weak triprotic acid, [that] is a very polar molecule ... soluble in water. ... Triprotic means that an orthophosphoric acid molecule can dissociate up to three times, giving up an H+ each time, which typically combines with a water molecule, H2O, as shown in these reactions:
- H3PO4(s) + H2O(l) <=> H3O+(aq) + H2PO4−(aq) Ka1= 7.25×10−3
- H2PO4−(aq)+ H2O(l) <=> H3O+(aq) + HPO42−(aq) Ka2= 6.31×10−8
- HPO42−(aq)+ H2O(l) <=> H3O+(aq) + PO43−(aq) Ka3= 3.98×10−13
The anion after the first dissociation, H2PO4−, is the dihydrogen phosphate anion. The anion after the second dissociation, HPO42−, is the hydrogen phosphate anion. The anion after the third dissociation, PO43−, is the phosphate or orthophosphate anion. For each of the dissociation reactions shown above, there is a separate acid dissociation constant, called Ka1, Ka2, and Ka3 given at 25 °C. Associated with these three dissociation constants are corresponding pKa1=2.12 , pKa2=7.21 , and pKa3=12.67 values at 25 °C."[4]
"For a given total acid concentration [A] = [H3PO4] + [H2PO4−] + [HPO42−] + [PO43−] ([A] is the total number of moles of pure H3PO4 which have been used to prepare 1 liter of solution), the composition of an aqueous solution of phosphoric acid can be calculated using the equilibrium equations associated with the three reactions described above together with the [H+][OH−] = 10−14 relation and the electrical neutrality equation. Possible concentrations of polyphosphoric molecules and ions is neglected. The system may be reduced to a fifth degree equation for [H+] which can be solved numerically, yielding:"[4]
| [A] (mol/L) | pH | [H3PO4]/[A] (%) | [H2PO4−]/[A] (%) | [HPO42−]/[A] (%) | [PO43−]/[A] (%) |
| 1 | 1.08 | 91.7 | 8.29 | 6.20×10−6 | 1.60×10−17 |
| 10−1 | 1.62 | 76.1 | 23.9 | 6.20×10−5 | 5.55×10−16 |
| 10−2 | 2.25 | 43.1 | 56.9 | 6.20×10−4 | 2.33×10−14 |
| 10−3 | 3.05 | 10.6 | 89.3 | 6.20×10−3 | 1.48×10−12 |
| 10−4 | 4.01 | 1.30 | 98.6 | 6.19×10−2 | 1.34×10−10 |
| 10−5 | 5.00 | 0.133 | 99.3 | 0.612 | 1.30×10−8 |
| 10−6 | 5.97 | 1.34×10−2 | 94.5 | 5.50 | 1.11×10−6 |
| 10−7 | 6.74 | 1.80×10−3 | 74.5 | 25.5 | 3.02×10−5 |
| 10−10 | 7.00 | 8.24×10−4 | 61.7 | 38.3 | 8.18×10−5 |
Phosphorylation
[edit | edit source]Def. "the process of transferring a phosphate group from a donor to an acceptor; often catalysed by enzymes"[5] is called phosphorylation.
- D-glucose + ATP → D-glucose-6-phosphate + ADP, Gibbs free energy (ΔG°) = −16.7 kJ/mol (° indicates measurement at standard condition)
Ubiquitylation
[edit | edit source]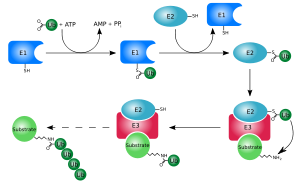
Ubiquitination (also known as ubiquitylation or ubiquitinylation) is an enzymatic post-translational modification in which a ubiquitin protein is attached to a substrate protein, most commonly to the last amino acid of ubiquitin (glycine 76) to a lysine residue on the substrate by an isopeptide bond between the carboxyl group (COO−) of the ubiquitin's glycine and the epsilon-amino group (ε-NH+
3) of the substrate's lysine.[6] Trypsin cleavage of a ubiquitin-conjugated substrate leaves a di-glycine "remnant" that is used to identify the site of ubiquitination.[7][8] Ubiquitin can also be bound to other sites in a protein which are electron-rich nucleophiles, termed "non-canonical ubiquitination".[9] This was first observed with the amine group of a protein's N-terminus being used for ubiquitination, rather than a lysine residue, in the protein MyoD[10] and has been observed since in 22 other proteins in multiple species,[11][12][13][14][15][16][17][18][19][20][21][22][23][24][25][26][27][12][28][29] including ubiquitin itself.[30][31] There is also increasing evidence for nonlysine residues as ubiquitination targets using non-amine groups, such as the thiol sulfhydryl group on cysteine,[26][27][32][33][34][35][36][37][38][39] and the hydroxyl group on threonine and serine.[26][27][32][38][39][40][41][42][43] The end result of this process is the addition of one ubiquitin molecule (monoubiquitination) or a chain of ubiquitin molecules (polyubiquitination) to the substrate protein.[44]
Ubiquitination requires three types of enzyme: ubiquitin-activating enzymes, ubiquitin-conjugating enzymes, and ubiquitin ligases, known as E1s, E2s, and E3s, respectively. The process consists of three main steps:
- Activation: Ubiquitin is activated in a two-step reaction by an E1 ubiquitin-activating enzyme, which is dependent on Adenosine triphosphate (ATP). The initial step involves production of a ubiquitin-adenylate intermediate. The E1 binds both ATP and ubiquitin and catalyses the acyl-adenylation of the C-terminus of the ubiquitin molecule. The second step transfers ubiquitin to an active site cysteine residue, with release of Adenosine monophosphate (AMP). This step results in a thioester linkage between the C-terminal carboxyl group of ubiquitin and the E1 cysteine thiol (sulfhydryl) group.[6][45] The human genome contains two genes that produce enzymes capable of activating ubiquitin: UBA1 and UBA6.[46]
- Conjugation: E2 ubiquitin-conjugating enzymes catalyse the transfer of ubiquitin from E1 to the active site cysteine of the E2 via a trans(thio)esterification reaction. In order to perform this reaction, the E2 binds to both activated ubiquitin and the E1 enzyme. Humans possess 35 different E2 enzymes, whereas other eukaryotic organisms have between 16 and 35. They are characterised by their highly conserved structure, known as the ubiquitin-conjugating catalytic (UBC) fold.[47]

- Ligation: E3 ubiquitin ligases catalyse the final step of the ubiquitination cascade. Most commonly, they create an isopeptide bond between a lysine of the target protein and the C-terminal glycine of ubiquitin. In general, this step requires the activity of one of the hundreds of E3s. E3 enzymes function as the substrate recognition modules of the system and are capable of interaction with both E2 and substrate. Some E3 enzymes also activate the E2 enzymes. E3 enzymes possess one of two domains: the homologous to the E6-AP carboxyl terminus (HECT) domain and the really interesting new gene RING finger domain (or the closely related U-box domain). HECT domain E3s transiently bind ubiquitin in this process (an obligate thioester intermediate is formed with the active-site cysteine of the E3), whereas RING domain E3s catalyse the direct transfer from the E2 enzyme to the substrate.[48] The anaphase-promoting complex (APC) and the SCF complex (for Skp1-Cullin-F-box protein complex) are two examples of multi-Protein subunit E3s involved in recognition and ubiquitination of specific target proteins for degradation by the proteasome.[49]
In the ubiquitination cascade, E1 can bind with many E2s, which can bind with hundreds of E3s in a hierarchical way. Having levels within the cascade allows tight regulation of the ubiquitination machinery.[50] Other ubiquitin-like proteins (UBLs) are also modified via the E1–E2–E3 cascade, although variations in these systems do exist.[51]
E4 enzymes, or ubiquitin-chain elongation factors, are capable of adding pre-formed polyubiquitin chains to substrate proteins.[52] For example, multiple monoubiquitylation of the tumor suppressor p53 by Mdm2[53] can be followed by addition of a polyubiquitin chain using P300-CBP coactivator family (p300 and CBP).[54][55]
Solubility
[edit | edit source]
2SO
4) in liquid water at high temperature is graphed. Credit: Stan J Klimas.
Under certain conditions, the equilibrium solubility can be exceeded to give a so-called supersaturated solution, which is metastable.[56]
According to the International Union of Pure and Applied Chemistry (IUPAC) definition,[57] solubility is the analytical composition of a saturated solution expressed as a proportion of a designated solute in a designated solvent. Solubility may be stated in various units of concentration such as molarity, molality, mole fraction, mole ratio, mass (solute) per volume (solvent) and other units.
The extent of solubility ranges widely, from infinitely soluble (without limit) (fully miscible[58]) such as ethanol in water, to poorly soluble, such as silver chloride in water. The term insoluble is often applied to poorly or very poorly soluble compounds. A number of other descriptive terms are also used to qualify the extent of solubility for a given application. For example, U.S. Pharmacopoeia gives the following terms:
| Term | Mass parts of solvent required to dissolve 1 mass part of solute[59] |
|---|---|
| Very soluble | <1 |
| Freely soluble | 1 to 10 |
| Soluble | 10 to 30 |
| Sparingly soluble | 30 to 100 |
| Slightly soluble | 100 to 1000 |
| Very slightly soluble | 1000 to 10,000 |
| Practically insoluble or insoluble | ≥ 10,000 |
The thresholds to describe something as insoluble, or similar terms, may depend on the application: one source states that substances are described as "insoluble" when their solubility is less than 0.1 g per 100 mL of solvent.[60]
Solubility (metastable, at concentrations approaching saturation) also depends on the physical size of the crystal or droplet of solute (or, strictly speaking, on the specific surface area or molar surface area of the solute).[61]
As the temperature is raised, gases usually become less soluble in water (to minimum, which is below 120 °C for most permanent gases[62]), but more soluble in organic solvents.[63]
The chart shows solubility curves for some typical solid inorganic salts (temperature is in degrees Celsius i.e. kelvins minus 273).[64] Many salts behave like barium nitrate and disodium hydrogen arsenate, and show a large increase in solubility with temperature. Some solutes (e.g., sodium chloride in water) exhibit solubility that is fairly independent of temperature. A few, such as calcium sulfate (gypsum) and cerium(III) sulfate, become less soluble in water as temperature increases.[65]
A few exceptions exist, such as certain cyclodextrins.[66]
For condensed phases (solids and liquids), the pressure dependence of solubility is typically weak and usually neglected in practice. Assuming an ideal solution, the dependence can be quantified as:
where the index i iterates the components, Ni is the mole fraction of the ith component in the solution, P is the pressure, the index T refers to constant temperature, Vi,aq is the partial molar volume of the ith component in the solution, Vi,cr is the partial molar volume of the ith component in the dissolving solid, and R is the universal gas constant.[67]
In the presence of small bubbles, the solubility of the gas does not depend on the bubble radius in any other way than through the effect of the radius on pressure (i.e., the solubility of gas in the liquid in contact with small bubbles is increased due to pressure increase by Δp = 2γ/r; see Young–Laplace equation).[68]
A popular aphorism used for predicting solubility is "like dissolves like" also expressed in the Latin language as "Similia similibus solventur".[69] This statement indicates that a solute will dissolve best in a solvent that has a similar chemical structure to itself. This view is simplistic, but it is a useful rule of thumb. The overall solvation capacity of a solvent depends primarily on its polarity.[70] For example, a very polar (hydrophilic) solute such as urea is very soluble in highly polar water, less soluble in fairly polar methanol, and practically insoluble in non-polar solvents such as benzene. In contrast, a non-polar or lipophilic solute such as naphthalene is insoluble in water, fairly soluble in methanol, and highly soluble in non-polar benzene.[71]
The rate of dissolution can be often expressed by the Noyes–Whitney equation or the Nernst and Brunner equation[72] of the form:
where:
- m = mass of dissolved material
- t = time
- A = surface area of the interface between the dissolving substance and the solvent
- D = diffusion coefficient
- d = thickness of the boundary layer of the solvent at the surface of the dissolving substance
- Cs = mass concentration of the substance on the surface
- Cb = mass concentration of the substance in the bulk of the solvent
Some substances may dissolve incongruently, whereby the composition of the solute in solution does not match that of the solid and is accompanied by alteration of the "primary solid" and possibly formation of a secondary solid phase, but in general, some primary solid also remains and a complex solubility equilibrium establishes; e.g. dissolution of albite may result in formation of gibbsite.[73]
- NaAlSi3O8(s) + H+ + 7H2O ⇌ Na+ + Al(OH)3(s) + 3H4SiO4.
The solubility of albite is expected to depend on the solid-to-solvent ratio, where it results in formation of metamorphic rocks.
Precipitation
[edit | edit source]
The diagram on the right shows the differences between a compound, a precipitate, a supernate, and a suspension.
Gas-solid interface reactions
[edit | edit source]Photochemical reactions
[edit | edit source]
Photoexcitation of a carbonyl group adds it to an olefin producing an oxetane.
Solid-state reactions
[edit | edit source]These reactions are usually governed by interdiffusion rates.
Hypotheses
[edit | edit source]- Chemical reactions often occur in small steps.
See also
[edit | edit source]References
[edit | edit source]- ↑ "Reaction Web".
- ↑ 2.0 2.1 M. Nic; J. Jirat; B. Kosata; A. Jenkins (24 February 2014). "IUPAC Gold Book". IUPAC. doi:10.1351/goldbook. ISBN 0-9678550-9-8. Retrieved 2015-08-08.
- ↑ "phosphoric acid". San Francisco, California: Wikimedia Foundation, Inc. June 17, 2013. Retrieved 2013-08-23.
- ↑ 4.0 4.1 "Phosphoric acid". San Francisco, California: Wikimedia Foundation, Inc. August 19, 2013. Retrieved 2013-08-22.
- ↑ SemperBlotto (17 May 2006). "phosphorylation, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 2017-09-17.
{{cite web}}:|author=has generic name (help) - ↑ 6.0 6.1 "Mechanisms underlying ubiquitination". Annual Review of Biochemistry 70: 503–33. 2001. doi:10.1146/annurev.biochem.70.1.503. PMID 11395416.
- ↑ "Direct identification of a G protein ubiquitination site by mass spectrometry". Biochemistry 41 (16): 5067–74. April 2002. doi:10.1021/bi015940q. PMID 11955054.
- ↑ "A proteomics approach to understanding protein ubiquitination". Nature Biotechnology 21 (8): 921–6. August 2003. doi:10.1038/nbt849. PMID 12872131.
- ↑ "Non-canonical ubiquitylation: mechanisms and consequences". The International Journal of Biochemistry & Cell Biology 45 (8): 1833–42. August 2013. doi:10.1016/j.biocel.2013.05.026. PMID 23732108.
- ↑ "A novel site for ubiquitination: the N-terminal residue, and not internal lysines of MyoD, is essential for conjugation and degradation of the protein". The EMBO Journal 17 (20): 5964–73. October 1998. doi:10.1093/emboj/17.20.5964. PMID 9774340. PMC 1170923. //www.ncbi.nlm.nih.gov/pmc/articles/PMC1170923/.
- ↑ "Proteasome-mediated degradation of p21 via N-terminal ubiquitinylation". Cell 115 (1): 71–82. October 2003. doi:10.1016/S0092-8674(03)00755-4. PMID 14532004.
- ↑ 12.0 12.1 "The ubiquitin-conjugating enzyme (E2) Ube2w ubiquitinates the N terminus of substrates". The Journal of Biological Chemistry 288 (26): 18784–8. June 2013. doi:10.1074/jbc.C113.477596. PMID 23696636. PMC 3696654. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3696654/.
- ↑ "The N-terminal domain of MyoD is necessary and sufficient for its nuclear localization-dependent degradation by the ubiquitin system". Proceedings of the National Academy of Sciences of the United States of America 105 (41): 15690–5. October 2008. doi:10.1073/pnas.0808373105. PMID 18836078. PMC 2560994. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2560994/.
- ↑ "N-Terminal ubiquitination of extracellular signal-regulated kinase 3 and p21 directs their degradation by the proteasome". Molecular and Cellular Biology 24 (14): 6140–50. July 2004. doi:10.1128/MCB.24.14.6140-6150.2004. PMID 15226418. PMC 434260. //www.ncbi.nlm.nih.gov/pmc/articles/PMC434260/.
- ↑ "N-terminal polyubiquitination and degradation of the Arf tumor suppressor". Genes & Development 18 (15): 1862–74. August 2004. doi:10.1101/gad.1213904. PMID 15289458. PMC 517406. //www.ncbi.nlm.nih.gov/pmc/articles/PMC517406/.
- ↑ "The tumor suppressor protein p16(INK4a) and the human papillomavirus oncoprotein-58 E7 are naturally occurring lysine-less proteins that are degraded by the ubiquitin system. Direct evidence for ubiquitination at the N-terminal residue". The Journal of Biological Chemistry 279 (40): 41414–21. October 2004. doi:10.1074/jbc.M407201200. PMID 15254040.
- ↑ "Lysine-independent turnover of cyclin G1 can be stabilized by B'alpha subunits of protein phosphatase 2A". Molecular and Cellular Biology 29 (3): 919–28. February 2009. doi:10.1128/MCB.00907-08. PMID 18981217. PMC 2630686. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2630686/.
- ↑ "Degradation of the E7 human papillomavirus oncoprotein by the ubiquitin-proteasome system: targeting via ubiquitination of the N-terminal residue". Oncogene 19 (51): 5944–50. November 2000. doi:10.1038/sj.onc.1203989. PMID 11127826.
- ↑ "Degradation of the epstein-barr virus latent membrane protein 1 (LMP1) by the ubiquitin-proteasome pathway. Targeting via ubiquitination of the N-terminal residue". The Journal of Biological Chemistry 275 (31): 23491–9. August 2000. doi:10.1074/jbc.M002052200. PMID 10807912.
- ↑ "Lysine-independent ubiquitination of Epstein-Barr virus LMP2A". Virology 300 (1): 153–9. August 2002. doi:10.1006/viro.2002.1562. PMID 12202215.
- ↑ "HSP70 protects BCL2L12 and BCL2L12A from N-terminal ubiquitination-mediated proteasomal degradation". FEBS Letters 583 (9): 1409–14. May 2009. doi:10.1016/j.febslet.2009.04.011. PMID 19376117.
- ↑ "N-terminal hemagglutinin tag renders lysine-deficient APOBEC3G resistant to HIV-1 Vif-induced degradation by reduced polyubiquitination". Journal of Virology 85 (9): 4510–9. May 2011. doi:10.1128/JVI.01925-10. PMID 21345952. PMC 3126286. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3126286/.
- ↑ "Ubiquitin-Proteasome-mediated degradation of Id1 is modulated by MyoD". The Journal of Biological Chemistry 279 (31): 32614–9. July 2004. doi:10.1074/jbc.M403794200. PMID 15163661.
- ↑ "Ubiquitin proteasome-dependent degradation of the transcriptional coactivator PGC-1{alpha} via the N-terminal pathway". The Journal of Biological Chemistry 285 (51): 40192–200. December 2010. doi:10.1074/jbc.M110.131615. PMID 20713359. PMC 3001001. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3001001/.
- ↑ "Degradation of the Id2 developmental regulator: targeting via N-terminal ubiquitination". Biochemical and Biophysical Research Communications 314 (2): 505–12. February 2004. doi:10.1016/j.bbrc.2003.12.116. PMID 14733935.
- ↑ 26.0 26.1 26.2 "Ubiquitylation on canonical and non-canonical sites targets the transcription factor neurogenin for ubiquitin-mediated proteolysis". The Journal of Biological Chemistry 284 (23): 15458–68. June 2009. doi:10.1074/jbc.M809366200. PMID 19336407. PMC 2708843. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2708843/.
- ↑ 27.0 27.1 27.2 "Non-canonical ubiquitylation of the proneural protein Ngn2 occurs in both Xenopus embryos and mammalian cells". Biochemical and Biophysical Research Communications 400 (4): 655–60. October 2010. doi:10.1016/j.bbrc.2010.08.122. PMID 20807509.
- ↑ "Ube2W conjugates ubiquitin to α-amino groups of protein N-termini". The Biochemical Journal 453 (1): 137–45. July 2013. doi:10.1042/BJ20130244. PMID 23560854. PMC 3778709. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3778709/.
- ↑ "Intrinsic disorder drives N-terminal ubiquitination by Ube2w". Nature Chemical Biology 11 (1): 83–9. January 2015. doi:10.1038/nchembio.1700. PMID 25436519. PMC 4270946. //www.ncbi.nlm.nih.gov/pmc/articles/PMC4270946/.
- ↑ "A proteolytic pathway that recognizes ubiquitin as a degradation signal". The Journal of Biological Chemistry 270 (29): 17442–56. July 1995. doi:10.1074/jbc.270.29.17442. PMID 7615550.
- ↑ "A ubiquitin ligase complex assembles linear polyubiquitin chains". The EMBO Journal 25 (20): 4877–87. October 2006. doi:10.1038/sj.emboj.7601360. PMID 17006537. PMC 1618115. //www.ncbi.nlm.nih.gov/pmc/articles/PMC1618115/.
- ↑ 32.0 32.1 "Ubiquitination of serine, threonine, or lysine residues on the cytoplasmic tail can induce ERAD of MHC-I by viral E3 ligase mK3". The Journal of Cell Biology 177 (4): 613–24. May 2007. doi:10.1083/jcb.200611063. PMID 17502423. PMC 2064207. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2064207/.
- ↑ "Ubiquitination on nonlysine residues by a viral E3 ubiquitin ligase". Science 309 (5731): 127–30. July 2005. doi:10.1126/science.1110340. PMID 15994556.
- ↑ "The specificities of Kaposi's sarcoma-associated herpesvirus-encoded E3 ubiquitin ligases are determined by the positions of lysine or cysteine residues within the intracytoplasmic domains of their targets". Journal of Virology 82 (8): 4184–9. April 2008. doi:10.1128/JVI.02264-07. PMID 18272573. PMC 2293015. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2293015/.
- ↑ "A conserved cysteine is essential for Pex4p-dependent ubiquitination of the peroxisomal import receptor Pex5p". The Journal of Biological Chemistry 282 (31): 22534–43. August 2007. doi:10.1074/jbc.M702038200. PMID 17550898.
- ↑ "Ubiquitination of mammalian Pex5p, the peroxisomal import receptor". The Journal of Biological Chemistry 282 (43): 31267–72. October 2007. doi:10.1074/jbc.M706325200. PMID 17726030.
- ↑ "A conserved cysteine residue of Pichia pastoris Pex20p is essential for its recycling from the peroxisome to the cytosol". The Journal of Biological Chemistry 282 (10): 7424–30. March 2007. doi:10.1074/jbc.M611627200. PMID 17209040. PMC 3682499. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3682499/.
- ↑ 38.0 38.1 "Apoptosis induction by Bid requires unconventional ubiquitination and degradation of its N-terminal fragment". The Journal of Cell Biology 179 (7): 1453–66. December 2007. doi:10.1083/jcb.200707063. PMID 18166654. PMC 2373500. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2373500/.
- ↑ 39.0 39.1 "Complex regulation controls Neurogenin3 proteolysis". Biology Open 1 (12): 1264–72. December 2012. doi:10.1242/bio.20121750. PMID 23259061. PMC 3522888. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3522888/.
- ↑ "Multilayered mechanism of CD4 downregulation by HIV-1 Vpu involving distinct ER retention and ERAD targeting steps". PLoS Pathogens 6 (4): e1000869. April 2010. doi:10.1371/journal.ppat.1000869. PMID 20442859. PMC 2861688. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2861688/.
- ↑ "Serine-threonine ubiquitination mediates downregulation of BST-2/tetherin and relief of restricted virion release by HIV-1 Vpu". Journal of Virology 85 (1): 51–63. January 2011. doi:10.1128/JVI.01795-10. PMID 20980512. PMC 3014196. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3014196/.
- ↑ "Serine residues in the cytosolic tail of the T-cell antigen receptor alpha-chain mediate ubiquitination and endoplasmic reticulum-associated degradation of the unassembled protein". The Journal of Biological Chemistry 285 (31): 23916–24. July 2010. doi:10.1074/jbc.M110.127936. PMID 20519503. PMC 2911338. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2911338/.
- ↑ "Ubiquitylation of an ERAD substrate occurs on multiple types of amino acids". Molecular Cell 40 (6): 917–26. December 2010. doi:10.1016/j.molcel.2010.11.033. PMID 21172657. PMC 3031134. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3031134/.
- ↑ "Ubiquitin ligases and beyond". BMC Biology 10: 22. March 2012. doi:10.1186/1741-7007-10-22. PMID 22420755. PMC 3305657. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3305657/.
- ↑ "Ubiquitin-like protein activation by E1 enzymes: the apex for downstream signalling pathways". Nature Reviews Molecular Cell Biology 10 (5): 319–31. May 2009. doi:10.1038/nrm2673. PMID 19352404. PMC 2712597. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2712597/.
- ↑ "Activating the ubiquitin family: UBA6 challenges the field". Trends in Biochemical Sciences 33 (5): 230–7. May 2008. doi:10.1016/j.tibs.2008.01.005. PMID 18353650.
- ↑ "The family of ubiquitin-conjugating enzymes (E2s): deciding between life and death of proteins". FASEB Journal 24 (4): 981–93. April 2010. doi:10.1096/fj.09-136259. PMID 19940261.
- ↑ "HECT and RING finger families of E3 ubiquitin ligases at a glance". Journal of Cell Science 125 (Pt 3): 531–7. February 2012. doi:10.1242/jcs.091777. PMID 22389392. PMC 3381717. //www.ncbi.nlm.nih.gov/pmc/articles/PMC3381717/.
- ↑ "Control of cell growth by the SCF and APC/C ubiquitin ligases". Current Opinion in Cell Biology 21 (6): 816–24. December 2009. doi:10.1016/j.ceb.2009.08.004. PMID 19775879. PMC 2805079. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2805079/.
- ↑ "Ubiquitin: structures, functions, mechanisms". Biochimica et Biophysica Acta 1695 (1–3): 55–72. November 2004. doi:10.1016/j.bbamcr.2004.09.019. PMID 15571809.
- ↑ "Modification of proteins by ubiquitin and ubiquitin-like proteins". Annual Review of Cell and Developmental Biology 22: 159–80. 2006. doi:10.1146/annurev.cellbio.22.010605.093503. PMID 16753028.
- ↑ "A novel ubiquitination factor, E4, is involved in multiubiquitin chain assembly". Cell 96 (5): 635–44. March 1999. doi:10.1016/S0092-8674(00)80574-7. PMID 10089879.
- ↑ "Human mdm2 mediates multiple mono-ubiquitination of p53 by a mechanism requiring enzyme isomerization". The Journal of Biological Chemistry 276 (33): 31357–67. August 2001. doi:10.1074/jbc.M011517200. PMID 11397792.
- ↑ "Polyubiquitination of p53 by a ubiquitin ligase activity of p300". Science 300 (5617): 342–4. April 2003. doi:10.1126/science.1080386. PMID 12690203.
- ↑ "CBP and p300 are cytoplasmic E4 polyubiquitin ligases for p53". Proceedings of the National Academy of Sciences of the United States of America 106 (38): 16275–80. September 2009. doi:10.1073/pnas.0904305106. PMID 19805293. PMC 2752525. //www.ncbi.nlm.nih.gov/pmc/articles/PMC2752525/.
- ↑ "Online Medical Dictionary". Newcastle University. January 25, 2009.
- ↑ International Union of Pure and Applied Chemistry (IUPAC) (1997). Solubility, In: Compendium of Chemical Terminology (2nd (the "Gold Book") ed.). http://goldbook.iupac.org/.
- ↑ Clugston M.; Fleming R. (2000). Advanced Chemistry (1st ed.). Oxford: Oxford Publishing. p. 108.
- ↑ "Pharmacopeia of the United States of America, 32nd revision, and the National Formulary, 27th edition," 2009, pp.1 to 12.
- ↑ Rogers, Elizabeth; Stovall, Iris (2000). "Fundamentals of Chemistry: Solubility". Department of Chemistry. University of Wisconsin. Retrieved 22 April 2015.
- ↑ G.T. Hefter, ed (2003). The Experimental Determination of Solubilities. Wiley-Blackwell. ISBN 0-471-49708-8.
- ↑ P. Cohen, ed (1989). The ASME handbook on Water Technology for Thermal Power Systems. The American Society of Mechanical Engineers. p. 442.
- ↑ John W. Hill, Ralph H. Petrucci, General Chemistry, 2nd edition, Prentice Hall, 1999.
- ↑ Handbook of Chemistry and Physics (27th ed.). Cleveland, Ohio: Chemical Rubber Publishing Co.. 1943.
- ↑ "What substances, such as cerium sulfate, have a lower solubility when they are heated?". Retrieved 28 May 2014.
- ↑ Salvatore Filippone; Frank Heimanna; André Rassat (2002). "A highly water-soluble 2+1 b-cyclodextrin–fullerene conjugate". Chem. Commun. 2002 (14): 1508–1509. doi:10.1039/b202410a.
- ↑ E.M. Gutman (1994). Mechanochemistry of Solid Surfaces. World Scientific Publishing Co..
- ↑ G.W. Greenwood (1969). "The Solubility of Gas Bubbles". Journal of Materials Science 4 (4): 320–322. doi:10.1007/BF00550401.
- ↑ Kenneth J. Williamson (1994). Macroscale and Microscale Organic Experiments (2nd ed.). Lexington, Massachusetts: D. C, Heath. p. 40. ISBN 0-669-19429-8.
- ↑ The solvent polarity is defined as its solvation power according to Reichardt
- ↑ Merck Index (7th ed.). Merck & Co.. 1960.
- ↑ Dokoumetzidis, Aristides; Macheras, Panos (2006). "A century of dissolution research: From Noyes and Whitney to the Biopharmaceutics Classification System". Int. J. Pharm. 321 (1–2): 1–11. doi:10.1016/j.ijpharm.2006.07.011. PMID 16920290. http://www.sciencedirect.com/science/article/pii/S0378517306005813.
- ↑ O.M. Saether, ed (1997). Geochemical processes, weathering and groundwater recharge in catchments. Rotterdam: Taylor & Francis. p. 6. ISBN 90-5410-641-7.









![{\displaystyle v=-{\frac {d[{\ce {A}}]}{dt}}=k\cdot [{\ce {A}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12291760fcaff20a02ff74abd0dfcb922664cddb)
![{\displaystyle {\ce {[A]}}(t)={\ce {[A]}}_{0}\cdot e^{-k\cdot t}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/498c37558508e2f7297604f93bb5408dcd8c3fd4)













