Talk:WikiJournal of Science/Spaces in mathematics
Add topic
WikiJournal of Science
Open access • Publication charge free • Public peer review • Wikipedia-integrated
Previous
Volume 1(1)
Volume 1(2)
Volume 2(1)
Volume 3(1)
Volume 4(1)
Volume 5(1)
Volume 6(1)
This article has been through public peer review.
It was adapted from the Wikipedia page Space_(mathematics) and contains some or all of that page's content licensed under a CC BY-SA license. Post-publication review comments or direct edits can be left at the version as it appears on Wikipedia.
First submitted:
Accepted:
Article text
PDF: Download
DOI: 10.15347/wjs/2018.002
QID: Q55120290
XML: Download
Share article
![]() Email
|
Email
| ![]() Facebook
|
Facebook
| ![]() Twitter
|
Twitter
| ![]() LinkedIn
|
LinkedIn
| ![]() Mendeley
|
Mendeley
| ![]() ResearchGate
ResearchGate
Suggested citation format:
Boris Tsirelson (1 June 2018). "Spaces in mathematics". WikiJournal of Science 1 (1): 2. doi:10.15347/WJS/2018.002. Wikidata Q55120290. ISSN 2470-6345. https://upload.wikimedia.org/wikiversity/en/c/cd/Spaces_in_mathematics.pdf.
Citation metrics
AltMetrics
Page views on Wikipedia
Wikipedia: This work is adapted from the Wikipedia article Space (mathematics) (CC BY-SA). Content has also subsequently been used to update that same Wikipedia article Space (mathematics).
License: ![]()
![]() This is an open access article distributed under the Creative Commons Attribution ShareAlike License, which permits unrestricted use, distribution, and reproduction, provided the original author and source are credited.
This is an open access article distributed under the Creative Commons Attribution ShareAlike License, which permits unrestricted use, distribution, and reproduction, provided the original author and source are credited.
Henry Hoff ![]() (handling editor) contact
(handling editor) contact
Markus Pössel ![]() contact
contact
Sylvain Ribault ![]() contact
contact
Article information
Plagiarism check
![]() Pass. WMF copyvio tool using TurnItIn.
Text found in external page but is attributed as quote, so not regarded as plagiarism. T.Shafee(Evo﹠Evo)talk 11:15, 9 January 2018 (UTC)
Pass. WMF copyvio tool using TurnItIn.
Text found in external page but is attributed as quote, so not regarded as plagiarism. T.Shafee(Evo﹠Evo)talk 11:15, 9 January 2018 (UTC)
First review
Comments by Marshall Sumter ,
- Space (mathematics) was submitted by IP 77.126.70.80 but authored by the Parent article editors. Who answers the reviews? w:User:Tsirel appears to be a major contributor with necessary and sufficient background to respond to the reviews. --Marshallsumter (discuss • contribs) 18:33, 5 June 2017 (UTC)
- The sentence ending in "compared to classical mathematics." has [citation needed]. The classical history period dates from around 2,000 to 1,000 b2k.
- Is a space defined as a universe, a class, or a set of points with some added structure?
- Since some structures do not change a set to a space, the phrase "some added structure" is vague. --Marshallsumter (discuss • contribs) 20:34, 1 May 2017 (UTC)
- "and the inner product is indicated enclosing in by angle brackets." to "and the inner product is indicated by enclosing in angle brackets."
- "In the ancient mathematics," should be "In ancient mathematics," --Marshallsumter (discuss • contribs) 23:03, 6 May 2017 (UTC)
- ""space" was a geometric abstraction of the three-dimensional space observed in the everyday life." to ""space" was a geometric abstraction of the three-dimensional space observed in everyday life."
- "The above-mentioned fixed point S is called homothetic center or center of similarity or center of similitude" to "The above-mentioned fixed point S is called the homothetic center, or center of similarity, or center of similitude." in w:Homothetic transformation.
Text comments:
The structure that every space has to be a space is called the norm. It is the real-valued function
This article should be demonstrating the relevance to science of mathematical spaces. --Marshallsumter (discuss • contribs) 23:01, 6 May 2017 (UTC)
w:Homothetic transformation should be condensed and included where "homotheties — into similar figures." are mentioned in w:Space (mathematics). --Marshallsumter (discuss • contribs) 21:09, 27 May 2017 (UTC)
There are 21 footnotes to Bourbaki and 3 to other authors. This article appears to be an abridged paraphrase of Bourbaki. --Marshallsumter (discuss • contribs) 00:10, 28 May 2017 (UTC)
You mention 65 spaces in the table at the bottom, but only describe 16 from the table in the article, some large numbers of times. An article on mathematical space should mention many more than 16 in some developmental form. --Marshallsumter (discuss • contribs) 01:25, 28 May 2017 (UTC)
Perhaps there is a bit more precise definition of a mathematical space:
Def. a "set along with a collection of finitary functions and relations"[1] is called a structure.
Def. "a set [of points] with [some] added structure",[2] is called a space. --Marshallsumter (discuss • contribs) 04:10, 8 June 2017 (UTC)
"In mathematics, a space is a set (sometimes called a universe) with some added structure." is from w:Space (mathematics), perhaps referring to w:Universe (mathematics). --Marshallsumter (discuss • contribs) 04:16, 8 June 2017 (UTC)
Perhaps w:WikiProject Mathematics can be contacted for responses to the reviews. --Marshallsumter (discuss • contribs) 19:14, 27 May 2017 (UTC)
Just FYI: here (Wikiversity) you can perform OR by synthesis or anyway you like! --Marshallsumter (discuss • contribs) 04:19, 8 June 2017 (UTC)
References
- ↑ Slimeknight (20 February 2010). structure. San Francisco, California: Wikimedia Foundation, Inc. https://en.wiktionary.org/wiki/structure. Retrieved 2017-06-07.
- ↑ Bkell (4 March 2008). Space (mathematics). San Francisco, California: Wikimedia Foundation, Inc. https://en.wikipedia.org/wiki/Space_(mathematics). Retrieved 2017-06-07.
To the editorial comments.
1. yes I do.
2. On Wikipedia I must avoid "Original Research", even OR by synthesis. Here I feel more free (hope I am not mistaken). That sentence is evidently true under any reasonable interpretation of "classical" and "modern". Well, 2000 to 1000 b2k. That time, "space" was roughly "the 3-dimensional Euclidean space" (in modern language, of course). Nowadays it means something completely different.
3. Universe? Do you mean "universe of cosmology", "mathematical universe", or what? Well, anyway: yes, a space is a set of points with some added structure.
4. Yes, I agree, it is vague. Probably, no one knows, why some mathematical structures are called spaces while others are not. This is an oddity of the natural language. It disappears when translating mathematics into a formal language (say, that of the set theory ZFC).
5, 6, 7, 8. Yes, thank you, I'll do these changes. Alas, I am not a native English speaker.
To the text comments.
A. Not every vector space is endowed with a norm. Try, for instance, the vector space of all real-valued functions on the real line. All functions! Generally, not bounded, not continuous, not measurable, etc. Using the choice axiom one can prove existence of (at least one) norm on this space. But can you choose one norm and say: this norm is inherent to this space? And, on the other hand: a norm makes no sense when a space is not (at least) a vector space; say, "a norm on a measure space" makes no sense.
B. Relevance to science? Hmmm... a challenge. I'll think.
C. Homotheties? Well, I'll try.
D. Yes, an abridged paraphrase of Bourbaki. Why not? This is not (and could not be) my research. I just want to explain to the perplexed, why these crazy mathematicians interpret the word "space" in a very strange way.
E. First, some spaces are more notable than others. Second, the table at the bottom is not mine, and I do not like it, since, for instance, "T2 space" is nothing but a topological space satisfying an additional condition; "Hausdorff space" is another name of the same notion; "Quotient space" is not a kind of space, but a collective name for a construction of spaces that emerges in the theory of topological spaces, as well as in the theory of vector spaces, etc etc.
Boris Tsirelson (discuss • contribs) 21:52, 6 June 2017 (UTC)
Imported; what now?
The article is imported hereto: Space (mathematics). It contains a lot of red links. What to do with them? Sometimes we have something appropriate here; for instance, I just changed [[Set (mathematics)|set]] to [[Set theory|set]]. What to do when we have nothing appropriate? Of course, I can change [[Euclid]] to [[w:Euclid|''Euclid'']] (using the slanted font as a hint on escape from Wikiversity), or just to Euclid (no link). What is better? Boris Tsirelson (discuss • contribs) 06:25, 8 June 2017 (UTC)
Also, I restored a table (Section "Differences") that was deleted as my OR by synthesis... Boris Tsirelson (discuss • contribs) 06:50, 8 June 2017 (UTC)
Comments by Marshall Sumter ,
- Is the Space (mathematics) that is here to be considered the submittal?
- Linking the red links to Wikipedia is okay, as is removing the links. It's your choice! --Marshallsumter (discuss • contribs) 23:05, 8 June 2017 (UTC)
1. Yes it is. (But I still change it.) Boris Tsirelson (discuss • contribs) 05:01, 9 June 2017 (UTC)
Linking to Wikipedia is a good choice. It can be replaced later if a learning resource exist. For the readers of the article it is sometimes important to look up the definition of mathematical expression. Therefore no learning resource in Wikiveristy is required in general for a specific term linked in the article. --Bert Niehaus (discuss • contribs) 12:44, 11 May 2018 (UTC)
Definition of mathematical space
According to Kevin Carlson:
- Neither of these words have a single mathematical definition. The English words can be used in essentially all the same situations, but you often think of a "space" as more geometric and a "structure" as more algebraic. The best approximation to a general "space" for many purposes is a topological space, but Grothendieck generalized further than that, to what are called topoi.
- In model theory a "structure" is a set in which we can interpret some logical language, which is to say a set with some distinguished elements and some functions and relations on it. Some of the most common languages structures interpret are those of groups, rings, and fields, which have no relations, functions are addition and/or multiplication, and distinguished identity elements for those operation. We also have the language of partially ordered sets, which has the relation ≤≤ and neither functions nor constants.
- So you could think of "structures" as places we do algebra, and "spaces" as places we do geometry. Then a lot of great mathematics has come from passing from structures to spaces and vice versa, as when we look at the fundamental group of a topological space or the spectrum of a ring. But in the end, the distinction is neither hard nor fast and only goes so far: many things are obviously both structures and spaces, some things are not obviously either, and some people might well disagree with everything I've said here.
Quoted from math.stackexchange, 2012 Boris Tsirelson (discuss • contribs) 08:04, 8 June 2017 (UTC)
Another source: Robert C. Reed, Review of Leo Corry, Modern Algebra and the Rise of Mathematical Structures. Some quotes:
- The book is therefore an attempt not merely to show how the concept of structure evolved, but to demonstrate that the concept itself is not strictly mathematical at all in the narrow sense [...] (p.183)
- Corry does not go so far as to call the rise of structure a scientific 'revolution' [...] but [...] it would not be too inaccurate to describe the theme of this book as the claim that the rise of structure can best be understood as a paradigm shift. (p. 184)
- In his book Corry uses italics to make a distinction between the structures Bourbaki defines formaly and the usual informal notion of structure. (p. 187)
- Corry does not seem to feel that any formal definition of structure could do justice to the use of the concept in actual mathematical practice [...] Corry's view could be summarized as the belief that 'structure' refers essentially to a way of doing mathematics, and is therefore a concept probably just as far from being precisely definable as the cultural artifact of mathematics itself. (p. 189, the end)
Boris Tsirelson (discuss • contribs) 08:30, 8 June 2017 (UTC)
The relevance to science and engineering
A quote from annotation to the book "Some Modern Mathematics for Physicists and Other Outsiders" (vol.1, 2014) by Paul Roman:
- The text then ponders on special algebraic systems, topological spaces, and topological spaces with special properties. Topics include complete metric spaces, compact spaces, separable and connected spaces, homeomorphism and isometry, convergence, continuity, general structure of topological spaces, rings and fields, linear spaces, linear algebras, and nonassociative algebras. The book elaborates on the theory of integration and measure spaces, including measurable spaces, general properties of the integral, and measureable functions.
- The publication is a valuable reference for theoretical physicists, research engineers, and scientists who are concerned with structural problems.
Boris Tsirelson (discuss • contribs) 19:53, 8 June 2017 (UTC)
A quote from Sect. 2.2 of "Mathematics and other disciplines" by V.G Masanja (2002):
- Examples of mathematical results that got inspired by physical ideas include Donaldson's proof of the existence of different differential structures on simply connected 4-dimensional manifolds. This has very deep consequences for quantum gravity [...] The new conservation laws developed in the last part of the 20th Century are believed to be the most fundamental in physics. The application of modern abstract mathematics in physics has resulted in astounding discoveries of the 20th Century in the physical sciences, the life sciences and technology.
Boris Tsirelson (discuss • contribs) 20:16, 8 June 2017 (UTC)
+ w:Simon_Donaldson + w:Exotic_R4 + w:Donaldson's theorem + Geometry and physics
And, of course, Hilbert spaces are indispensable in quantum physics, as well as Einstein spaces in general relativity (including black holes, Big Bang etc). Boris Tsirelson (discuss • contribs) 20:21, 8 June 2017 (UTC)
Also, mathematically, quantum gravity is a theory of a random metric space that is two-dimensional topologically, but four-dimensional metrically! See Quantum Gravity: the Mathematics of Random Metrics by Oded Schramm (2008). Boris Tsirelson (discuss • contribs) 20:32, 8 June 2017 (UTC)
Also, affine and projective spaces are used in computer vision and robotics, see the lecture Introduction to Computer Vision for Robotics of this course; and Chapter 7 "Algebraic curves in structure from motion" by Kaminski and Teicher, pp. 245–296 in book: Computer Vision and Robotics (ed. John X. Liu) Nova Publishers, 2006. Boris Tsirelson (discuss • contribs) 07:53, 9 June 2017 (UTC)
Revised
So, the manuscript is revised according to the first review. Boris Tsirelson (discuss • contribs) 20:18, 10 June 2017 (UTC)
First revision review
Comments by Marshall Sumter ,
In the table,
- "the space is three-dimensional" to "space is three-dimensional",
- "the space is the universe of geometry" to "space is the universe of geometry",
After the table,
- "in the axioms of the projective geometry" to "in the axioms of projective geometry",
- "in the Euclidean geometry but meaningless in the projective geometry." to "in Euclidean geometry but meaningless in projective geometry.",
- "The non-Euclidean hyperbolic geometry, introduced by" to "Non-Euclidean hyperbolic geometry, introduced by",
- "Analytic geometry made a great progress" to "Analytic geometry made great progress",
- "the heritage of the classical geometry was lost." to "the heritage of classical geometry was lost.",
- "(called also smooth manifold)" to "(also called smooth manifold)",
- "The question "what is the sum of the three angles of a triangle" makes sense in a Euclidean space but not in a projective space; these are spaces of different types." to "The question "what is the sum of the three angles of a triangle" makes sense in a Euclidean space but not in a projective space.",
- "Isomorphisms to itself are called automorphisms." to "An isomorphism to itself is called an automorphism.",
- Although you only use the term "functor" once, if the Wikipedia description of a "functor" is acceptable, a link to functor may be helpful,
- "A curve in a Riemann space has the length." to "A curve in a Riemann space has length.",
- "(called also standard Borel spaces)" to "(also called standard Borel spaces)",
- "but no infinite-dimensional Lebesgue measure." to "but no infinite-dimensional Lebesgue measures.",
- "A topological space becomes also a measurable space when endowed with the Borel σ-algebra." to "A topological space also becomes a measurable space when endowed with Borel σ-algebra.",
- "as when we look at the fundamental group of a topological space or the spectrum of a ring." to "as when we look at the fundamental group of a topological space or the w:spectrum of a ring.", if the Wikipedia description is acceptable, and
- "it embraces all types of spaces mentioned in Sect. 2.3" to "it embraces all types of spaces mentioned in Sect. 2.3[5]", if this is where "Sect. 2.3" is. --Marshallsumter (discuss • contribs) 00:41, 14 June 2017 (UTC)
General comments:
I like it! Take a look at the above to see if you agree, or not, with these suggestions, and change accordingly! --Marshallsumter (discuss • contribs) 00:41, 14 June 2017 (UTC)
- Nice. All done. Boris Tsirelson (discuss • contribs) 06:16, 14 June 2017 (UTC)
Second review
Review by anonymous peer reviewer ,
These assessment comments were submitted on , and refer to this previous version of the article
The following sorts of spaces might be worth mentioning. Their definitions are elaborate, so a complete description of each may not be advisable:
- Schemes
- Algebraic spaces (linked at the bottom, but otherwise omitted)
- Algebraic and Deligne-Mumford stacks
- Locales
These are important because:
- Algebraic spaces, algebraic stacks, Deligne-Mumford stacks, and locales do not literally have points! The first three get their "spacey-ness" by defining what an "algebraic map" from a scheme into the space is. The last gets its "spacey-ness" by imitating the lattice of open sets of a topological space.
- Schemes do have a set of points, but morphisms (therefore isomorphisms) of schemes are not determined by their values on points. For example, the scheme consists of a single point. There is only one function from a single point to a single point, but there are infinitely many isomorphisms : we get an isomorphism corresponding to each via the ring map fixing and taking to .
In other words, these kinds of spaces break - or at least do not make direct use of - the paradigm of mathematical spaces being solely sets of points with extra structure. What remains is that a mathematical space is something that can be described in the language of mathematics and which has a visual sense to it.
- True, the recent trend toward "pointless geometry" is (for now) outside the scope of this article. True, sometimes geometric intuition appears to be helpful even in the absence of points. True, the corresponding definitions tend to be prohibitively elaborate for this lightweight not-so-technical survey. Moreover, the (more accessible) definitions of "pointful" spaces are omitted here. The (formal, rigorous) definitions codify the preexisting (informal, non-rigorous) intuition. Here I try to convey the intuition; motivated readers can find definitions in linked more technical articles.
- I would be glad to convey the intuition behind "pointless spaces", too, but I cannot. This is beyond my competence. I never used such spaces in my research. I would be happy to have a coauthor able to enlarge this survey accordingly. Boris Tsirelson (discuss • contribs) 06:26, 3 November 2017 (UTC)
- In the absence of such coauthor I do my best by adding four paragraphs to Section "Spaces and structures". Boris Tsirelson (discuss • contribs) 09:00, 7 November 2017 (UTC)
- However, today w:User:Ozob added two relevant sections to w:Space (mathematics). Boris Tsirelson (discuss • contribs) 06:44, 24 November 2017 (UTC)
- To my regret, Ozob prefers to not disclose his real-life name. Thus I copy his two relevant (sub)sections to this preprint. Boris Tsirelson (discuss • contribs) 08:00, 25 November 2017 (UTC)
Editorial comment
Comments by Thomas Shafee ,
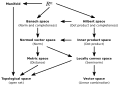
The good people at the Commons Graphic Lab have come up with two vectorised version of figure 1:
-
SVG
-
Alternative SVG
Comment on Diagram: "Topological Vector Spaces" instead of "Vectorspace". Looking at the diagram, it seems to me that, that "Vector Space" should be replaced by "Topological Vector Spaces" due to the fact that a vector space with a topology of open set is a topological vector space in which and are continuous. Then also an arrow from "Topological Vector Spaces" to "Topological Spaces" would be correct. --Bert Niehaus (discuss • contribs) 12:56, 11 May 2018 (UTC)
Please choose which you think is the most appropriate, or give further feedback for their improvement at this page. T.Shafee(Evo﹠Evo)talk 01:58, 4 November 2017 (UTC)
- Wow... Yes, the "Alternative SVG" version is better. Boris Tsirelson (discuss • contribs) 07:33, 4 November 2017 (UTC)
As an additional editorial recommendation whilst you're working on the other comments: I think that the article would benefit from more inline citations to the references. Some sections currently don't cite any references, making verification and followup by readers more difficult. In general there should be at least one citation per paragraph, even if the same reference is cited multiple times. I'm happy to compromise if this particularly conflicts with the expectations of your field. T.Shafee(Evo﹠Evo)talk 02:57, 8 November 2017 (UTC)
- Oops!
- Wikipedia
- succeeds as an encyclopedia due to,
- but fails as a learning resource because of,
- the following.
- On Wikipedia I am not an expert; I cannot say "this is true", but only "this is well-known, see these sources". In contrast, in a math journal, a textbook, or a popular science text, I can say "this is true", meaning "this is true according to my expertise, plus expertise of referee(s), plus expertise of editor(s)".
- "... we have to avoid injecting our own perspective and vision into articles we write here. But that perspective and vision is exactly what would be necessary to give a good course on a topic. We aren't trying to give a course here, though, just a reference." Carl 13:09, 20 October 2017
- "I do think that there is a difference between presenting a reference on a topic and presenting a textbook or expository essay. This difference is somewhat captured by the quote "The purpose of Wikipedia is to present facts, not to teach subject matter." from WP:NOT." Carl 20:21, 24 October 2017
- "Wiki seems to be a bad medium for writing textbooks or preparing learning materials ... the great courses and textbooks are about personal touches and visions." Taku 23:46, 29 October 2017
- Wikipedia (being encyclopedia) is tertiary; math journals are primary; textbooks are secondary. What about WikiJournal of Science? Is it primary? secondary? tertiary?
- "There is a big difference in the citation styles in academic literature and textbooks between history and mathematics. In history virtually every statement is someones interpretation and needs citations. In mathematics most basic information, like trigonometric identities are backed by mathematical proof so are not controversial. All text books will cite these without reference." Salix alba 12:12, 17 October 2017
- On Wikipedia I cannot explain a point that is not explained already (in reliable sources). What here? Boris Tsirelson (discuss • contribs) 07:02, 8 November 2017 (UTC)
- As far as I see, the "sections that don't cite any references" contain a lot of links to Wikipedia. Doesn't it help "verification and followup by readers"? Boris Tsirelson (discuss • contribs) 07:26, 8 November 2017 (UTC)
Comments by Thomas Shafee ,
My apologies for the slow response. You are correct that mathematical articles tend to be more sparsely sourced than the sciences (though some Wikipedia articles contain more references, example). For original research articles, only established information needs to be referenced. However for review articles, it is preferred that sources are given for as much of the text as possible (I've also updated the author guidelines to help clarify).
It is my opinion that citing sources is still useful in an encyclopedic review article, since the text is bringing together established work, even if the references would just be to basic textbooks, or other reviews. Indeed, my comment only really applies to the Types of spaces section, since I think that he others are adequately referenced. However, I will also consult the opinions of the other editorial board members. T.Shafee(Evo﹠Evo)talk 03:01, 25 November 2017 (UTC)
- Thank you for the clarification. The "Types of spaces" section is a survey with many subsections, and each subsection is a lightweight introduction into a topic treated in depth in one or several Wikipedia articles that are linked; these linked articles cite sources. The same can be said about my "w:Conditioning (probability)". There, the lead ends with the phrase "This article concentrates on interrelations between various kinds of conditioning, as shown mostly by examples. For systematic treatment (and corresponding literature) see more specialized articles mentioned below". This way it survives on Wikipedia since 2008. Also "Space (mathematics)" survives there since 2009. Well, I know that I am on the wedge of w:WP:SYNTH; my articles are somewhat encyclopedic, somewhat essays; they are in danger of attack, and indeed, "Conditioning (probability)" is marked by "Unsourced material may be challenged and removed. (May 2009)". Maybe they survive only by w:WP:IAR. And indeed, summary style does not relieve me of the duty of reliable sources. (This is why I seek alternative outlets for my explanatory essays.) On the other hand, facts presented in the "Types of spaces" section are of very basic nature, should be well-known to everyone already acquainted with the spaces considered, and contained in nearly every relevant textbook. Also, you wrote "references would just be to basic textbooks, or other reviews"; a link to a Wikipedia article, isn't it a reference to other review?
- So, I see such alternatives:
- Borrow sources from the linked Wikipedia articles and copy them hereto (leads to terribly long bibliography).
- Write in the lead "For systematic treatment (and corresponding literature) see more specialized articles mentioned below" and leave to wikipedians the decision to tolerate it or not.
- Proclaim the article to be an explanatory essay not intended for inclusion into Wikipedia.
- Your opinion? Boris Tsirelson (discuss • contribs) 10:16, 25 November 2017 (UTC)
Third review
Review by Gaëtan Borot , Max Planck Institut for Mathematics, Bonn
These assessment comments were submitted on , and refer to this previous version of the article
This article offers a historical and conceptual perspective on the meta-notion of space in mathematics. Such an entreprise is useful, first for mathematics practioners to reflect on the epistemology of their field and the state of things they live in and regularly use, second for scholars of other fields to have an introductory overview of the meta-notions used in mathematics, and third for non-specialists who are curious about the language used by mathematicians. In this respect, I find that the article reaches these goals and praise the author(s) for this reflection : it is rather accessible (at least for people who have some familiarity with abstraction) at the beginning, and progressive, and it is introductory (as a overview wiki article should be), avoiding lengthy discussions, with a good balance between examples, formalization of a meta-notion, and historical discussion.
If the targeted readership is supposed to be broad, it may be useful to test the article with a reviewer who is a scholar or a student of a very different field (for instance, from literature/philosophy/arts), which could possibly lead to some adjustments and give an idea of the perception by an outsider. In particular, there are many different species of spaces mentioned, and the way the vocabulary is formed and the notion are nested with each other, although familiar for people trained in mathematics and well done here for mathematical standards, may turn out to be a bit too opaque for non practitioners.
I list below detailed comments, following the order of appearance in the text. They point either typos, or suggest minor modifications or ask for disambiguation of meaning. I have only two strong recommendations - expand the mention of non-commutative geometry into a section (as it illustrates very well the limits of the notion of space and geometry, and would complete the description of the perspectives taken by mathematicians on space up to modern research) - erase or substantially rework the last section "Mathematical spaces in science and engineering", which is far below the standards of what can be expected for an encyclopedia article, even for an opening conclusion (see 38.) -- while I appreciated the quality of the rest of the article.
1. In ancient mathematics, "space" was a geometric abstraction of the three-dimensional space observed in everyday life : it is a bit unfortunate that the first sentence contains an auto-reference. Perhaps use a different word, e.g. "environment" or "world" ?
Ancient mathematics : was that abstraction put forward by the Greeks only (in that case it may be more accurate to say Ancient Greek mathematics, or also other ancient civilizations (e.g. Egyptians, Babylonians) ?
2. "Completely justified this theory" : could this be made more precise ? Is it meant "realized", or that hyperbolic geometry was not only a fancy of abstraction in regard to the more established euclidean geometry ?
3. The metaphor of theater actors afterwards is interesting, but what is meant by "only mimic" is not clear to me. To make the analogy more striking, perhaps say "while the nature of objects (the individual actors performing the play) is not."
4. Add French accentuation: Géométrie descriptive of Monge.
5. Figure 2 : the simplicity of the figure would make easy for the author to make its own for this wiki contribution, which is perhaps preferable (unless the author of the figure was itself a contributor to that article).
6. In the beginning of the paragraph "Golden age and afterwards : dramatic change", geometry itself has not been given a definition. Perhaps a comment on such a definition (as spaces are the main object that geometry aims to study) as well on the etymology (metría : measurement ; gê : earth). Although initially geometry was about studying the properties of the space we live in (and objects therein) and the globe, the use of this word was then extended widely (as the notion of space in question here).
7. I suggest to make additions about the notion of dimension, so that a reader with few mathematical training can have some rough idea of the concepts listed and avoiding the impressions he reads a list of existing concepts. For instance, "The algebraic concept of dimension applies to vector space, and captures the number of degrees of freedom/(how much information is needed to specify a point) in that space". Perhaps it should be mentioned that the other concepts of dimension like Hausdorff dimension or inductive dimension rather rely on the relative size of subregions compared to the size of their boundaries. And that all these notions agree in the case of (finite-dimensional) vector spaces.
8. In "Also, a three-dimensional projective space ... four-dimensional vector space": "is now defined non-classically" is a bit ambiguous. Maybe you want to say that the definition of three-dimensional projective space nowadays is different from the classical.
9. In the last paragraph before "Taxonomy of spaces", I feel the example given somehow artificial. First, what is meant by "more geometric than others" is ambiguous and subjective. Second, I suspect that the reason that a smooth manifold is not called differentiable space comes from the history of mathematics that led to isolate the notion of manifold: a rather particular kind of space, with definitions that could be disputed depending on the singular behavior one may want to allow, and many objects that are not manifolds with this definition and led to propose new definitions. It is only to avoid linguistic ambiguity that manifold was adopted instead of space -- not really in relation with the very content of the concept and the assumed properties of a "manifold" or the rich geometry it may host. Differential space sounds a correct name for a manifold for the intuition I have of modern taxonomy standards (also, beware of the linguistic abuse in identifying differentiable and smooth, whose extent may differ from language to language), and also as is commented on later in the article.
I also see another way to understand this paragraph as written by the author: namely it could point out that being called "space" is a sign of higher "geometricity", but it is not the case because other things that could have been called space were actually not for linguistic reasons. If this is what the author meant, the fact that it is so for linguistic reasons/necessity of disambiguation should be underlined.
At first read I understood something else, namely that some things called space are more geometric than others things that don't deserve to be called space due to what they actually are (subjectively ; if I want to specify what this subjectivity relies on : I would say some structure is "very geometric" if it can be equipped with a lot extra structures and with groups acting on them, and emphasizing that gives a lot of information on that structure). If I may try to dig an example to illustrate this: infinity categories are not called space (because it seems a higher level notion than that of space) but it can be argued this is a quite geometric notion, and some models used to define infinity categories are strongly based on simplicial sets and therefore geometric intuition (one such model for category is for instance called Segal space ...).
To conclude this comment, I would at least amend the sentence "One may expect ..." -- which I think is welcome here -- to say something like "are perceived more geometric than others" and choose another example, with a few explanations to disambiguate (or allow clear identifications of) the possible readings of this paragraph.
10. "Upper-level classification" is exemplified but not defined. I feel the need for some more formal of description of what it means, as infering what is meant from the examples is sometimes incomplete, and it seems to point to elements of classification could nevertheless be clearly verbalized here. I also say that because this "three level classification" does not come with any reference (only correspondence of the first two with Bourbaki), so I suppose (?) that it is a construction or reformulation of the author ; I am not a priori opposing this presentation, but a reformulation to be more precise would be necessary for the "upper-level" layer (I am content with the presentation of the two other layers). For instance, the statement "the third level classifies up to isomorphism" is rather clear, and I would like to see the same thing for the "upper-level". Also, for the exposition, it is perhaps more clear-cut to first write a short paragraph giving a brief description of the three layers (with no example). And then give details, examples and more explanation.
In the subsequent paragraph I find the distinction and comments about univalent vs multivalent theories very appropriate to be mentioned here.
11. "Motion and reflection": is motion a mathematical notion ? Shouldn't one rather say "rotations, reflections and compositions thereof" ?
12. "since each real number is also a complex number". I would add : "More generally, a vector space over a field also has the structure of a vector space over a subfield of that field".
13. "However, orthogonal ... ". I would add something like : "This is because no extra structure (like a scalar product) has been provided in a linear space to measure angles".
14. "Dimension of a topological space" > "The dimension of a topological space".
"... covering dimensions are used" > "can be used".
15. "manifolds ... locally isomorphic to Euclidean space". I would rather say : to finite-dimensional topological vector space (the Euclidean metric is a extra structure that does not a priori glue globally). And I would add : "and satisfying a few extra properties". I am thinking here about Hausdorff, second countable, etc. Same remark (linear instead of Euclidean) appears and should be corrected in the section about schemes.
16. "A straight line ... $(n+1)$-dimensional linear space". I find this presentation a bit confusing, in particular because what "its" is referring to is unclear (same remark for the projective space paragraph). Could it be reformulated ?
17. "Every incomplete space ..." : the information that incomplete spaces have a completion is missing. One may reformulate e.g. : "Every incomplete space has a (minimal) completion in which it is isometrically embedded".
18. "Linear topological spaces are complete ... in infinite dimensions" : this sentence should be moved at the end of the first paragraph, as it is odd to put it after the discussion of uniform spaces.
19. "Vectors in a Euclidean space are a linear space" : what does that mean (the verb "be" seem incorrect) ?
20. "it may be a polygon (on the plane)". I would add : "or more generally a polytope (in arbitrary dimensions)
21. "is its inner product to itself" > "with itself"
22. "An inner product space is a (real or complex) ". I would rather say "is a real (or complex)" to match with (or sesquilinear) afterwards.
23. that's forgotten > that forgot
24. "the length of the shortest curve is the distance" > "the length of the shortest curve between two points defines the distance between these two points"
25. "pseudo-Riemann spaces very important for GR" > "pseudo-Riemann spaces, which are very important for GR".
26. "A measure generalizes area, etc." > "A measure generalizes the notion of area, etc."
27. Could one (or two) remarks be added to say why standard measurable (probability) spaces are especially useful ?
28. when endowed with Borel sigma-algebra > with the Borel sigma-algebra
29. defined by the basic arithmetic operations > defined from
30. a commutative ring, the global sections ... > a commutative ring, namely the ring of global sections ...
31. an enormous number of interesting schemes > I would favor a more neutral formulation, like "many interesting schemes"
32. In DM stacks: I am not sure that the qualificative "non-algebraic" for the singularities is appropriate (in light of the example). A -orbifold singularity looks algebraic to me (it occurs in the curve of equation ). What I would call non algebraic is with irrational.
33. It would be necessary to justify the statement that "Grothendieck considered topoi his greatest achievement" by a reference.
34. "and infinitely many types to be used (or not) in the future" : the statement looks bold and I would tame it by saying foreseeable future.
35. not even used by Bourbaki himself: do you mean here participants to the Bourbaki group, or in the mathematical treaties written by Bourbaki?
36. A comment: the question of denomination space vs. structure bears some analogy to the question of denomination particles vs. waves in modern physics. Interestingly this has not caused to formulation of any paradox by mathematics practitioners -- as opposed to the debates in early quantum physics.
37. The discussion feels incomplete without a section (or at least a paragraph) of its own describing non-commutative geometry. Besides, rather than a Mathoverflow discussion, a more appropriate reference about the nature of non-commutative geometry would be to Connes. I also raise the question whether online forum discussions are suitable for references in a wiki article, because 1) of the possible instability of this reference with time (would it be (freely) accessible in 5 years, 10 years, etc. ?) -- the answer is not necessarily negative as for instance the arxiv established itself as a stable online resource over a period of 30 years, but deserves to be analyzed case by case ; 2) of the possible (lack of) authority/knowledgeability of the forum contributors or evaluation thereof ; 3) the possible future evolution of forum discussions. It does not pose any problem when the full quotation is written down (like Carlson's quote), as it is just the matter of fair attribution. I however find it problematic how "discussed on Mathoverflow" appears at the end of this article.
38. The content of "Mathematical spaces in science and engineering" is too light and fuzzy in my taste to be included in a wiki article. I suggest to erase it or it should be completely rewritten with the same seriousness as the rest of the article. The examples given in the engineering paragraph raise the question (only online courses, fairly recent): why those examples and references (and not others) ? what will be their relevance time passing ? I do not understand either the information brought by the content of the paragraph "engineering and science". The last paragraph "Contemporary theoretical physics" is too light and vague to add any value to the article. The writing style used for the last sentence has a taste of (empty) sensationalism which the reader of a wiki can be spared. Given the scarcity of references used in the whole article (which I did not feel unjustified for such an introductory article), I am tempted to see the inclusion of 2 references on Liouville quantum gravity alone as counterproductive name dropping. It could certainly make sense to include Liouville quantum gravity when moduli spaces are mentioned earlier in the text, as an example of moduli space where points themselves describe certain spaces or geometric structures in order to emphasize the nestings of abstraction that can be hidden in the concept of space (projective spaces and moduli space of algebraic curve, but they could emphasize this remark). If Liouville quantum gravity is to be mentioned, it should be placed in the context of current research, and in a broader (and more fundamental) context of random metric spaces. Liouville gravity being a (though interesting) trendy topic since 15 years in modern research is perhaps the only (in my opinion, bad) reason why it has been included here. Choosing it as the single example given to illustrate the use spaces in modern theoretical physics is rather narrowminded and at odds with the higher perspective and generality embraced by all the previous paragraphs. Besides, the logical link between the two sentences of this very last paragraph is weak.
- Thank you! Quite helpful.
- Everything is done (hopefully), except for the following items.
- 15. "manifolds ... locally isomorphic to Euclidean space" – Not quite so; rather, it is written "manifolds ... locally homeomorphic to Euclidean space". Thus, only the topology of the Euclidean space is relevant. The Euclidean metric is as irrelevant as the affine structure. It is not about w:piecewise linear manifold versus "piecewise Euclidean manifold". Surely we can write "to finite-dimensional topological vector space", but this is a bit longer, a bit less accessible, and ultimately equivalent.
- 18. "it is odd to put it after the discussion of uniform spaces" – A linear topological space need not be metrizable; completeness makes sense for uniform (rather than topological) spaces; the phrase "Every linear topological space ... is also a uniform space" precedes the discussion of its completeness.
- 34: "the statement looks bold and I would tame it by saying foreseeable future" – Really? As for me, "to be used (or not)" is not a statement at all (being trivially true anyway); and I doubt that "infinitely many types" are to be used in a finite time. :-)
- 32, 33, 37: I need the help of the co-author ("Ozob"). I try to contact him, but he does not answer yet. :-(
- Boris Tsirelson (discuss • contribs) 19:52, 7 April 2018 (UTC)
- Update: a new subsection "Non-commutative geometry" is created by Ozob. Item 37 now done. Boris Tsirelson (discuss • contribs) 07:04, 8 April 2018 (UTC)
- Sorry; I'm traveling with my family and haven't been as prompt as I would have liked. I was able to finish the new section but didn't have time to reply here until now.
- ?. While I don't quite know where it fits, Dedekind's reflections on the relation between real numbers and points on a line seem relevant. Quoting from Stetigkeit und irrationale Zahlen, appearing in Beman, W. W., ed. and trans., Essays on the Theory of Numbers:
In the preceding section attention was called to the fact that every point p of the straight line produces a separation of the same into two portions such that every point of one portion lies to the left of every point of the other. I find the essence of continuity in the converse, i. e., in the following principle:
“If all points of the straight line fall into two classes such that every point of the first class lies to the left of every point of the second class, then there exists one and only one point which produces this division of all points into two classes, this severing of the straight line into two portions.”
As already said I think I shall not err in assuming that every one will at once grant the truth of this statement; the majority of my readers will be very much disappointed in learning that by this commonplace remark the secret of continuity is to be revealed. To this I may say that I am glad if every one finds the above principle so obvious and so in harmony with his own ideas of a line; for I am utterly unable to adduce any proof of its correctness, nor has any one the power.- 31. It is very hard to overstate the importance of projective space and projective varieties to algebraic geometry. (And also to number theory; concepts as elementary as height depend upon a choice of projective embedding.) Classically (prior to about 1950 or so), only projective varieties and their subvarieties were studied; even after abstract algebraic varieties were defined, it was not clear that proper but non-projective varieties existed. I prefer not to be neutral if it will mislead the reader; I think whatever phrasing is used should communicate the centrality of projective space. Or perhaps there's a quotation we can find somewhere?
- 32. The curve (or ) is a scheme with a singularity at the origin. It is not an orbifold; it is still a plain scheme, just as a Whitney stratified space is still a topological space. The DM stack , where is the cyclic group of order n acting by rotation about the origin, is not a scheme. It has an orbifold singularity at the origin. When I wrote "non-algebraic", I meant, "is not a scheme or algebraic space," which is a common usage within algebraic geometry. However, I can see how this might be confusing. Perhaps it would be better to say, "but they allow for certain singularities that cannot be described using schemes."
- 33. I was thinking of Grothendieck's reflections on his work in Récoltes et Semailles; but it seems that I remembered it a little wrong. According to Wikipedia's Alexander Grothendieck article, he called topoi "central" to his work; however I was unable to verify the citation in the article, so it might be that he wrote something else. Probably it would be best to quote him here.
- Ozob (discuss • contribs) 01:30, 10 April 2018 (UTC)
- I have made edits to the corresponding Wikipedia article that I believe address the concerns above. Ozob (discuss • contribs) 05:45, 14 April 2018 (UTC)
- I have integrated these changes into the current draft. Assuming I've done so correctly, I believe the current article is satisfactory. Ozob (discuss • contribs) 04:57, 15 April 2018 (UTC)
- I have made edits to the corresponding Wikipedia article that I believe address the concerns above. Ozob (discuss • contribs) 05:45, 14 April 2018 (UTC)
- Authors' response is thus completed. Boris Tsirelson (discuss • contribs) 07:00, 15 April 2018 (UTC)
Follow-up
Review by Gaëtan Borot , Max Planck Institut for Mathematics, Bonn
These assessment comments were submitted on , and refer to this previous version of the article
- @Ozob: a precise reference to Grothendieck that can be used for topoi is p58 of Recoltes et Semailles: "Il [the theme of topoi] est ce que j'ai conçu de plus vaste, pour saisir avec finesse, par un même langage riche en résonances géométriques, une "essence" commune à des situations des plus éloignées les unes des autres, provenant de telle région ou de telle autre du vaste universe des choses mathématiques."
- In "Relations between species of spaces": The comment "(and moreover, ... large groupoids)" will only be understood by people for which the content of this section is obvious, it uses notions that have not been (even vaguely) defined in the text so far. So I suggest to remove it.
- I suggest to put "canonical" (in quotes) or so-called "canonical" instead of just canonical. Indeed, the meaning of the word canonical in mathematics is probably not known outside, and the sentence already rephrases clearly what it means, so one may want to emphasize that it actually defines what one means by canonical, by the above suggested modification.
- I would replace "The non-commutative C*-algebras, therefore, can be interpreted as non-commutative spaces, much like non-commutative von Neumann algebras" by a more suggestive formulation, like "Non-commutative geometry is the study, for a given non-commutative C^* algebra $A$ of the geometry of an imaginary space $X$ for which $A$ would be isomorphic to $C_0(X)$. This means for instance obtaining equivalent constructions of standard geometric tools to study "commutative spaces" directly starting from their algebra of functions, and generalizing these constructions to the setting of non-commutative algebras."
- Just to comment: I like that now the examples at the end of Spaces and structures remain at a rather elementary level.
- Items 2 and 3: done. Boris Tsirelson (discuss • contribs) 20:20, 25 May 2018 (UTC)
- Items 1 and 4: done. This completes our response. Ozob (discuss • contribs) 19:37, 27 May 2018 (UTC)
Editorial comments
Comments by Sylvain Ribault ,
I have started an editorial review of the article, with the aims of checking how the third reviewer's comments have been taken into account, and of assessing the structure and clarity of the text. When I think of a local improvement, I make an edit myself: such edits should be understood as suggestions, and the authors may revert them. I also plan to suggest more substantial improvements eventually, without performing the changes myself. Sylvain Ribault (discuss • contribs) 19:32, 15 April 2018 (UTC)
- Nice; but this edit bothers me. Every field is a (one-dimensional) linear space (over itself); is it necessarily topological? And, is this detail unneeded? Boris Tsirelson (discuss • contribs) 04:48, 20 April 2018 (UTC)
- First of all, please treat these edits as suggestions. I find it more convenient to edit the text than to write a message suggesting that you edit the text. But I do not expect the authors to follow all these suggestions. In the case of the edits where I deleted "(real or complex)", did you mean that your statements only hold if the field is or ? If yes, this important restriction should maybe not be between parentheses. Sylvain Ribault (discuss • contribs) 19:05, 20 April 2018 (UTC)
- Yes, I did mean it. Now restored, without the parentheses. Boris Tsirelson (discuss • contribs) 20:42, 20 April 2018 (UTC)
- First of all, please treat these edits as suggestions. I find it more convenient to edit the text than to write a message suggesting that you edit the text. But I do not expect the authors to follow all these suggestions. In the case of the edits where I deleted "(real or complex)", did you mean that your statements only hold if the field is or ? If yes, this important restriction should maybe not be between parentheses. Sylvain Ribault (discuss • contribs) 19:05, 20 April 2018 (UTC)
- Now I bother about affine spaces. Yes, "shifting it by a vector external to it, one obtains a n-dimensional affine space"; but this is not quite the definition of affine space. This is why I wrote "Given SUCH affine space..." rather than "Given AN affine space..." afterwards. In fact, an affine space is isomorphic to such shifted linear subspace; in other words, can be embedded this way into a linear space; but "CAN BE embedded" does not mean "IS embedded". True, my text is not crystal clear, it gives the idea (rather than definition) of affine space. But I am afraid that, in order to be crystal clear, it must be a textbook rather than a lightweight introduction into the big picture. The textbook would be considerably more boring and long. Boris Tsirelson (discuss • contribs) 20:51, 21 April 2018 (UTC)
- Now reformulated. A bit pedantic, but hopefully, clear enough. Boris Tsirelson (discuss • contribs) 05:21, 22 April 2018 (UTC)
Substantial remarks and suggestions:
- The section The_golden_age_and_afterwards was messed up by this edit by Ozob. Some paragraphs now seem out of place, in particular 'Functions are important...' and 'In order to fully appreciate...'. Sylvain Ribault (discuss • contribs) 22:27, 24 April 2018 (UTC)
- The discussion of the concepts of dimension might be out of place in the historical section The_golden_age_and_afterwards, and might fit better in the taxonomic section. Sylvain Ribault (discuss • contribs) 22:30, 24 April 2018 (UTC)
- The paragraph that starts with 'In terms of Bourbaki[7] the upper-level classification...' is obscure, and should be clarified. (Or deleted?) In particular, I do not understand what 'it is not the same' refers to. Sylvain Ribault (discuss • contribs) 22:33, 24 April 2018 (UTC)
- So many types of spaces are considered, that more figures like Figure 1 would be welcome. Ideally, one figure per subsection in the section Types of spaces. Sylvain Ribault (discuss • contribs) 22:40, 24 April 2018 (UTC)
- The subsection on non-commutative geometry is much more historical than the rest of the section. Is there a good reason for that? If not, could it be made more descriptive? Sylvain Ribault (discuss • contribs) 22:44, 24 April 2018 (UTC)
- Is there any relation between the discussion of commutative algebra in the context of schemes, and non-commutative geometry? Sylvain Ribault (discuss • contribs) 22:47, 24 April 2018 (UTC)
- I fail to understand the sentence 'The most important example of this is projective space.' Example of what exactly? And what are the definition and status of "projective space"? Sylvain Ribault (discuss • contribs) 22:50, 24 April 2018 (UTC)
- Thank you. I start working on Items 2, 3, 4. Items 1, 5, 6, 7 are up to Ozob; I'll notify him. Boris Tsirelson (discuss • contribs) 15:16, 25 April 2018 (UTC)
- 1. When I initially read "The golden age and afterwards", I thought it seemed disjointed, and I didn't think it fit well together. I tried to reorganize it so that it was more coherent; but if I understand you right you are saying I failed. That's fine. We can revert back to the earlier version if that's better.
- 5. That section exhausts my knowledge of non-commutative geometry. I am far from an expert in the subject; I barely knew enough to write what I did. A more descriptive treatment would require the attention of someone besides me. However, somewhere I gained the impression that the two classes of algebras mentioned, the von Neumann algebras and the C*-algebras, are really at the heart of the subject and are the main objects of study.
- 6. Not really. There is a subject called non-commutative algebraic geometry, but it is more like non-commutative algebra than it is like non-commutative geometry. It is also extremely difficult, and last I heard, despite many decades of work, the subject has not even progressed to the point where it can offer a satisfactory general definition of space, only of certain special types of spaces (specifically, non-commutative affine and projective schemes). I am told there are many counterexamples and impossibility results, though.
- 7. "This" refers to "not affine". Projective spaces were defined earlier in the article, under "Affine and projective spaces".
- Ozob (discuss • contribs) 03:54, 26 April 2018 (UTC)
- On Item 1: reading again "The golden age and afterwards" I see the logic: Coordinatization. Algebraization. Arithmetization. Dimension, higher and infinite. Boris Tsirelson (discuss • contribs) 13:08, 28 April 2018 (UTC)
- All done, unless Ozob proposes diagrams for "Non-commutative geometry", "Schemes", 'Topoi". Boris Tsirelson (discuss • contribs) 13:15, 28 April 2018 (UTC)
- Ozob proposes two more diagrams. I'll implement these. Boris Tsirelson (discuss • contribs) 04:46, 29 April 2018 (UTC)
Very good work on item 4. I would further suggest that Figure 6 be rearranged so that it is easier to read and that arrows do not cross. This is possible if you have 'complete metric', 'complete uniform' and 'complete linear topological' on the first line, then 'metric', 'uniform', 'linear topological' on the second line. Sylvain Ribault (discuss • contribs) 21:27, 28 April 2018 (UTC)
On item 1, the simplest improvement that could be done would be to delete the paragraph starting with "In order to fully appreciate the generality of this approach". Or at least to explicitly state what "this approach" refers to. But, as the use of the verb "appreciate" implies, this paragraph is vague and subjective. Sylvain Ribault (discuss • contribs) 21:44, 28 April 2018 (UTC)
On item 7, thanks for the explanation, I have edited the corresponding paragraph to make it clearer. Sylvain Ribault (discuss • contribs) 22:16, 28 April 2018 (UTC)
- Regarding item 1, I agree with your suggested deletion and have carried it out. I also thought it was an improvement to move a paragraph up. I am satisfied with the article as it presently stands. Ozob (discuss • contribs) 03:46, 2 May 2018 (UTC)
- About Figure 6. Sure, it looks nicer if arrows do not cross. But, first, with these two crossings it is still not a "spaghetti". And second, on all these pictures, all injective arrows are horizontal (to the right), and all other ("forgetful") arrows are vertical (to the bottom), which gives some meaning to the vertical dimension. I am reluctant to break this rule on Figure 6. Boris Tsirelson (discuss • contribs) 19:01, 2 May 2018 (UTC)
- After changing Figures 5, 8 (minor) and 11, I am also satisfied with the article.
- Authors' response is thus completed. Boris Tsirelson (discuss • contribs) 19:48, 2 May 2018 (UTC)
Commentary by non-specialist editor
Comments by Ian Alexander ,
The 'History' and 'Taxonomy of spaces' are I think as readable as they can
be, carrying the reader along and giving a feeling for the historical
development of the idea of spaces in mathematics. The taxonomy is a step
up in difficulty from the history, introducing a succession of concepts,
but in a simple way I felt that I could follow the drift of what was being
explained.
'Types of spaces' is considerably more difficult again, and the number of concepts introduced is rather large. The figures are welcome, and with their logical structure (reminiscent of diagrams in software engineering) both comforting and helpful points of reference. I do not believe there is anything that could be done to the text to make it easier, unless one was willing to construct examples and diagrams of them to illustrate the general points made: but this would stray from the argument, and would make the article much longer, to no benefit to mathematicians.
I was struck, as another reviewer was, by the small number of citations for an article which surveys so much ground. I would not wish to tell mathematicians how to cite mathematical papers, but plainly many more published articles are being referred to than are in fact cited. I note, too, that the author feels that wikilinks to existing articles fulfil much of the function of citations, a point of view at odds with Wikipedian theory and practice. I can see that mathematical papers might be able to rely rather more than those in other areas on the rather carefully-written articles on mathematical topics in Wikipedia. However, those too are often rather light on citations, so there is some danger of an infinite regress if everyone is pointing at other places which point to somewhere where, surely, a citation must be found.
I note, too, that statements like "For more information on mathematical structures see Wikipedia: mathematical structure, equivalent definitions of mathematical structures, and transport of structure." would not ordinarily be accepted in Wikipedia article text, but would be relegated to a 'See also' section or to 'Further' links at the head of a text section. I can see that there might reasonably be a mapping between the structure and conventions of a WJSci paper and the corresponding article, rather than identity; this would imply a defined or at least definable procedure to import a paper to Wikipedia.
In one place (at the top of 'Spaces and structures') the author has used "According to Kevin Carlson," with an embedded external link, which I do think would be better replaced with a citation.
I hope these brief comments from a non-mathematician may be of some service.
Having a review by a non-specialist was suggested in the third review of this article. The suggested changes are not critical for WikiJSci, but would facilitate the integration into Wikipedia. Sylvain Ribault (discuss • contribs) 21:59, 4 May 2018 (UTC)
- See also a relevant essay by Ian Alexander. As for me, it shows that Wikipedia is inherently different from any journal (traditional or wiki-based). Boris Tsirelson (discuss • contribs) 06:59, 5 May 2018 (UTC)
- Thanks, Boris. I agree, and it's the reason why the Journal is at least one step separated from Wikipedia, so we can accommodate differences from Wikipedia practice if necessary. (Ian Alexander) Chiswick Chap (discuss • contribs) 09:16, 5 May 2018 (UTC)
- Yes. Here is but one reason not to give the refs. Basic spaces (linear, topological, smooth etc) are treated in dozens, maybe hundreds of textbooks. I could go to a library and find some. What now? How to choose? Those available in our library need not be those available in the library of the reader. Those I like need not be those he/she likes. Let him/her go to a library and find something; it should be easy, unless he/she is too much unprepared to read anything like that (in which case a reference is of no help anyway). Boris Tsirelson (discuss • contribs) 10:07, 5 May 2018 (UTC)
- I just tried google search on "textbook on linear space" (without quotes). The result is convincing. The same for "textbook on topological space". Maybe this is why a number of professional mathematicians behave on Wikipedia like newbies even after many years of participation. Boris Tsirelson (discuss • contribs) 10:13, 5 May 2018 (UTC)
- Thank you for checking, I expect that will be fine then. As I said, it isn't for me to say what you should do, and journal papers can and will diverge from Wikipedia practice, but I felt I should mention it. Chiswick Chap (discuss • contribs) 10:46, 5 May 2018 (UTC)
- Thanks, Boris. I agree, and it's the reason why the Journal is at least one step separated from Wikipedia, so we can accommodate differences from Wikipedia practice if necessary. (Ian Alexander) Chiswick Chap (discuss • contribs) 09:16, 5 May 2018 (UTC)
Editorial comment
Comments by Sylvain Ribault ,
One last suggestion to the authors: could you improve the abstract? By abstract we actually mean a lead section in the sense of Wikipedia, see this discussion. The existing abstract is very short for such a long article, and the Bourbaki quote is not easy to understand in this context. Many readers will go no further than the abstract, so it would be good to concisely state the article's main points there, in a way that is accessible to non-mathematicians.
- I did; please look. Boris Tsirelson (discuss • contribs) 05:42, 11 May 2018 (UTC)
- I have suggested changes that tend to emphasize simplicity and readability. Sylvain Ribault (discuss • contribs) 21:55, 12 May 2018 (UTC)
- "elements of a set, or functions on another space, or subspaces of another space" — it may seem that functions on another space are not elements of a set.
- I think 'elements of a set' should come first, as 'spaces of spaces' sound like circular reasoning. The potential confusion that you point out would not bother me in the lead section of an encyclopedic review article. Sylvain Ribault (discuss • contribs) 21:57, 12 May 2018 (UTC)
- "uniquely determined by Euclid's axioms" — not quite so; the ancient axiomatics misses some things.
- Again, such subtleties are probably not for the lead section. It would be great to find a formulation that was both precise and readable, but this might not be possible. Maybe adding a footnote would be appropriate? Sylvain Ribault (discuss • contribs) 22:01, 12 May 2018 (UTC)
- OK, now a footnote. Boris Tsirelson (discuss • contribs) 05:17, 13 May 2018 (UTC)
- Again, such subtleties are probably not for the lead section. It would be great to find a formulation that was both precise and readable, but this might not be possible. Maybe adding a footnote would be appropriate? Sylvain Ribault (discuss • contribs) 22:01, 12 May 2018 (UTC)
- "relation from Euclidean to topological spaces" — is it usual to say "relation from ... to ..." (rather than "between")?
- The following sentence starts with 'Relations of this kind', so we need to use the word 'relation'. I agree that this use may not be common. Sylvain Ribault (discuss • contribs) 22:04, 12 May 2018 (UTC)
- "if an isomorphism ... is a one-to-one correspondence..." — it sounds like "if 2+2=4", doesn't it?
- Right, I have now tried to rectify the formulation. Sylvain Ribault (discuss • contribs) 22:06, 12 May 2018 (UTC)
- Boris Tsirelson (discuss • contribs) 21:43, 12 May 2018 (UTC)
Abstract/Lead Section - Contribution to scientific community
Scientific articles contribute something to scientific community. Due to the fact that Wiki Journal of Science is not meant to a Journal just for mathematical community, an abstract could contain sentence like "The article contributes .... to the scientific community ... by the analysis/revision/extension/development/a new method .... of ....". Such a recommended sentence might be valuable for the readers. This comment might be relevant for the reviewing of submitted papers to this journal in general. --Bert Niehaus (discuss • contribs) 13:07, 11 May 2018 (UTC)
- Looking at the 8+1 other upcoming articles I did not find such sentence (not even once). Boris Tsirelson (discuss • contribs) 18:24, 11 May 2018 (UTC)
Pictures in PDF
I am glad to see the article accepted.
About the PDF version. My pictures in svg format are converted from pdf (and adapted a little to low resolution). If needed, I can provide the pdf files (for high resolution). Should I do? Which way? Boris Tsirelson (discuss • contribs) 06:15, 1 June 2018 (UTC)
- The svg format will likely be fine. The adaptations for low-resolution will likely be relatively useful for the final PDF version. An optional change might be to use a sans-serif font in the images, however that is merely an aesthetic preference. T.Shafee(Evo﹠Evo)talk 06:28, 1 June 2018 (UTC)
- Yes, but it probably means conversion back and forth (pdf->svg->pdf) which is generally undesirable. Boris Tsirelson (discuss • contribs) 08:34, 1 June 2018 (UTC)
Volume 5?
"Suggested citation format: Tsirelson, B; et al. (2018). "Spaces in mathematics". WikiJournal of Science 5 (1). ISSN 2470-6345." – Really, 5(1)? Boris Tsirelson (discuss • contribs) 18:09, 1 June 2018 (UTC)
It seems I understand what happens. In "Template:Article info" I see
"|volume = Volume number (if left blank, will be autocalculated from year)".
Boris Tsirelson (discuss • contribs) 21:39, 2 June 2018 (UTC)
Now fixed. Boris Tsirelson (discuss • contribs) 21:43, 2 June 2018 (UTC)
DOI twice?
Now I see DOI twice:
- PDF: In preparation
- DOI: 10.15347/wjs/2018.002
- XML: In preparation
- Share article
- Email | Facebook | Twitter | LinkedIn | Mendeley
- Suggested citation format:
- Tsirelson, B; et al. (2018). "Spaces in mathematics". WikiJournal of Science 1 (1): 2. doi:10.15347/wjs/2018.002. ISSN 2470-6345.
Is it intended? Boris Tsirelson (discuss • contribs) 05:46, 3 June 2018 (UTC)
- Yes, the first mention is part of the metadata list, the second mention is simply part of the recommended citation for copy-pasting. It's actually a little old fashioned to do this, but I think it worthwhile for the WikiJournals initially to ensure that readers understand how to cite the articles. T.Shafee(Evo﹠Evo)talk 06:23, 3 June 2018 (UTC)
LaTeX problem? Or cache problem?
Something is wrong, maybe temporarily. For example, Sect. "Normed, Banach, inner product, and Hilbert spaces": the formula <math>\lVert x\rVert</math> gives "?'"`UNIQ--postMath-00000002-QINU`"'?". Should give Boris Tsirelson (discuss • contribs) 17:39, 16 June 2018 (UTC)
Null edit did not help. Boris Tsirelson (discuss • contribs) 17:42, 16 June 2018 (UTC)
Purge did not help (recommended here, here). Boris Tsirelson (discuss • contribs) 17:51, 16 June 2018 (UTC)
Old versions demonstrate the same problem. Boris Tsirelson (discuss • contribs) 17:53, 16 June 2018 (UTC)
Without "article info" template I still see the same problem, here. Boris Tsirelson (discuss • contribs) 18:01, 16 June 2018 (UTC)
And even just <math>x</math> on the first line gives the same. Boris Tsirelson (discuss • contribs) 18:06, 16 June 2018 (UTC)
Caught! I blame the parameter "part=Part 2" of the "cite book" template! Boris Tsirelson (discuss • contribs) 18:29, 16 June 2018 (UTC)
Interestingly, this parameter is just removed on Wikipedia, see this diff. Wow! Аn applause to w:User:Donnowin1. Boris Tsirelson (discuss • contribs) 18:35, 16 June 2018 (UTC)