Quizbank/University Physics Semester 2/Questions list
This table shows which questions are on each test. NTotal is the total number of questions from which the tests are created. If that number is excessive and the questions are repetitive, then, a smaller number NPrint<NTotal will intead be printed here.
Questions
[edit | edit source]Taken from University Physics Semester 2153341821922

- a) 5.768E-14 N
- b) 6.344E-14 N
- c) 6.979E-14 N
- d) 7.677E-14 N
- e) 8.444E-14 N

- a) 5.217E+01 degrees
- b) 5.739E+01 degrees
- c) 6.313E+01 degrees
- d) 6.944E+01 degrees
- e) 7.639E+01 degrees

is an integral that calculates the z-component of the electric field at point P situated above the x-axis where a charged rod of length (a+b) is located. The distance between point P and the x-axis is z=1.8 m. Evaluate at x=0.83 m if a=1.1 m, b=1.9 m. The total charge on the rod is 2 nC.
- a) 1.040E+00 V/m2
- b) 1.145E+00 V/m2
- c) 1.259E+00 V/m2
- d) 1.385E+00 V/m2
- e) 1.523E+00 V/m2
- a) 4.608E+09 N/C2
- b) 5.069E+09 N/C2
- c) 5.576E+09 N/C2
- d) 6.134E+09 N/C2
- e) 6.747E+09 N/C2
5)
is an integral that calculates the magnitude of the electric field at a distance fromthe center of a thin circular disk as measured along a line normal to the plane of the disk. The disk's radius is and the surface charge density is . Evaluate at .
- a) 2.021E+00 V/m2
- b) 2.224E+00 V/m2
- c) 2.446E+00 V/m2
- d) 2.691E+00 V/m2
- e) 2.960E+00 V/m2
6) A large thin isolated square plate has an area of 9 m2. It is uniformly charged with 8 nC of charge. What is the magnitude of the electric field 3 mm from the center of the plate's surface?
- a) 5.020E+01 N/C
- b) 5.522E+01 N/C
- c) 6.074E+01 N/C
- d) 6.681E+01 N/C
- e) 7.349E+01 N/C
7) What is the magnitude of the electric field at the origin if a 2.9 nC charge is placed at x = 5.9 m, and a 2.7 nC charge is placed at y = 9.2 m?
- a) 8.02 x 10-1N/C
- b) 9.26 x 10-1N/C
- c) 1.07 x 100N/C
- d) 1.23 x 100N/C
- e) 1.43 x 100N/C
8) What angle does the electric field at the origin make with the x-axis if a 1.3 nC charge is placed at x = -9 m, and a 1.5 nC charge is placed at y = -5.2 m?
- a) 4.15 x 101degrees
- b) 4.8 x 101degrees
- c) 5.54 x 101degrees
- d) 6.4 x 101degrees
- e) 7.39 x 101degrees
9) A dipole at the origin consists of charge Q placed at x = 0.5a, and charge of -Q placed at x = -0.5a. The absolute value of the x component of the electric field at (x,y) =( 4a, 3a) is βkQ/a2, where β equals
- a) 4.1 x 10-3
- b) 4.96 x 10-3
- c) 6.01 x 10-3
- d) 7.28 x 10-3
- e) 8.82 x 10-3
10) A dipole at the origin consists of charge Q placed at x = 0.5a, and charge of -Q placed at x = -0.5a. The absolute value of the y component of the electric field at (x,y) =( 1.1a, 1.2a) is βkQ/a2, where β equals
- a) 1.61 x 10-1
- b) 1.95 x 10-1
- c) 2.36 x 10-1
- d) 2.86 x 10-1
- e) 3.47 x 10-1
11) A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)?
(assuming ) , where
- a) −7
- b) −3
- c) −3
- d) 3
- e) 2
12) A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the y component of the electric field at the point (5, 1)?
(assuming ) , where :
- a) 5
- b) s−4
- c) 5−s
- d) 1−s
- e) s−1
13) A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the y component of the electric field at the point (5, 1)?
(assuming ) , where :
- a) 1/2
- b) 2/3
- c) 2
- d) 3/2
- e) 3
14) A line of charge density λ situated on the x axis extends from x = 3 to x = 7. What is the x component of the electric field at the point (7, 8)?
(assuming ) , where :
- a) s−3
- b) 3−s
- c) 8
- d) s−7
- e) 7−s
15) A line of charge density λ situated on the x axis extends from x = 3 to x = 7. What is the x component of the electric field at the point (7, 8)?
(assuming ) , where :
- a) 72 + (8−s)2
- b) 72 + 82
- c) (7-s)2 + 82
- d) 72 + (3−s)2
- e) 32 + 82
16) A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)?
(assuming ) , where
- a) 3−s
- b) 3
- c) s−7
- d) 7−s
- e) s−3
17) A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)?
(assuming ) , where
- a) 2
- b) 3
- c) 3/2
- d) 1/2
18) A line of charge density λ situated on the y axis extends from y = 2 to y = 7. What is the y component of the electric field at the point (2, 9)?
(assuming ) , where :
- a) 2
- b) s − 2
- c) 2 − s
- d) s − 9
- e) 9 − s
19) A line of charge density λ situated on the y axis extends from y = 2 to y = 7. What is the y component of the electric field at the point (2, 9)?
(assuming ) , where :
- a) 92 + (7-s)2
- b) 92 + (2-s)2
- c) 72 + (2-s)2
- d) 22 + (7-s)2
- e) 22 + (9-s)2
20) A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the y component of the electric field at the point (8, 4)?
(assuming ) , where :
- a) 1/2
- b) 4
- c) 2
- d) 8
21) A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the y component of the electric field at the point (8, 4)?
(assuming ) , where :
- a) s−8
- b) 8−s
- c) s−4
- d) 4−s
- e) 4
22) A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the x component of the electric field at the point (8, 4)?
(assuming ) , where :
- a) s−8
- b) 8−s
- c) s−4
- d) 4−s
- e) 4
23) A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the x component of the electric field at the point (5, 1)?
(assuming ) , where :
- a) 5
- b) s−4
- c) 5−s
- d) 1−s
- e) s−1
- a) 6.445E+01 N·m2/C
- b) 7.089E+01 N·m2/C
- c) 7.798E+01 N·m2/C
- d) 8.578E+01 N·m2/C
- e) 9.436E+01 N·m2/C

- a) 2.058E+01 N·m2/C
- b) 2.264E+01 N·m2/C
- c) 2.491E+01 N·m2/C
- d) 2.740E+01 N·m2/C
- e) 3.014E+01 N·m2/C

- a) 2.662E+01 N·m2/C
- b) 2.929E+01 N·m2/C
- c) 3.222E+01 N·m2/C
- d) 3.544E+01 N·m2/C
- e) 3.898E+01 N·m2/C
27) What is the magnetude (absolute value) of the electric flux through a rectangle that occupies the z=0 plane with corners at (x,y)= (x=0, y=0), (x=4, y=0), (x=0, y=6), and (x=4, y=6), where x and y are measured in meters. The electric field is,
- a) 3.658E+02 V·m
- b) 4.024E+02 V·m
- c) 4.426E+02 V·m
- d) 4.869E+02 V·m
- e) 5.355E+02 V·m
28) Five concentric spherical shells have radius of exactly (1m, 2m, 3m, 4m, 5m).Each is uniformly charged with 2.8 nano-Coulombs. What is the magnitude of the electric field at a distance of 3.5 m from the center of the shells?
- a) 6.171E+00 N/C
- b) 6.789E+00 N/C
- c) 7.467E+00 N/C
- d) 8.214E+00 N/C
- e) 9.036E+00 N/C
29) A non-conducting sphere of radius R=1.7 m has a non-uniform charge density that varies with the distnce from its center as given by ρ(r)=ar1.6 (r≤R) where a=3 nC·m-1.4. What is the magnitude of the electric field at a distance of 1.4 m from the center?
- a) 1.327E+02 N/C
- b) 1.460E+02 N/C
- c) 1.606E+02 N/C
- d) 1.767E+02 N/C
- e) 1.943E+02 N/C
30) A cylinder of radius, r=3, and height, h=4, is centered at the origin and oriented along the z axis. A vector field can be expressed in cylindrical coordinates as,
Let be the outward unit normal to this cylinder and evaluate ,
over the top surface of the cylinder.
- a) 6.908E+02
- b) 8.369E+02
- c) 1.014E+03
- d) 1.228E+03
- e) 1.488E+03
31) A cylinder of radius, r=3, and height, h=4, is centered at the origin and oriented along the z axis. A vector field can be expressed in cylindrical coordinates as,
Let be the outward unit normal to this cylinder and evaluate ,
over the curved side surface of the cylinder.
- a) 6.457E+02
- b) 7.823E+02
- c) 9.477E+02
- d) 1.148E+03
- e) 1.391E+03
32) A cylinder of radius, r=3, and height, h=4, is centered at the origin and oriented along the z axis. A vector field can be expressed in cylindrical coordinates as,
Let be the outward unit normal to this cylinder and evaluate ,
over the entire surface of the cylinder.
- a) 6.46E+02
- b) 7.82E+02
- c) 9.48E+02
- d) 1.15E+03
- e) 1.39E+03
33) A cylinder of radius, R, and height H has a uniform charge density of . The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z > H/2?
- a)
- b)
- c)
- d) none of these are correct
- e)
34) A cylinder of radius, R, and height H has a uniform charge density of . The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z < H/2?
- a)
- b) none of these are correct
- c)
- d)
- e)
35) A sphere has a uniform charge density of , and a radius or R. What formula describes the electric field at a distance r > R?
- a) none of these are correct
- b)
- c)
- d)
- e)
36) A sphere has a uniform charge density of , and a radius equal to R. What formula describes the electric field at a distance r < R?
- a)
- b)
- c) none of these are correct
- d)
- e)
37) A cylinder of radius, R, and height H has a uniform charge density of . The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r < R?
- a)
- b)
- c)
- d) none of these are correct
- e)
38) A cylinder of radius, R, and height H has a uniform charge density of . The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r > R?
- a)
- b)
- c)
- d) none of these are correct
- e)
39) A 5 C charge is separated from a 9 C charge by distance of 15 cm. What is the work done by increasing this separation to 21 cm?
- a) 7.003E-07 J
- b) 7.704E-07 J
- c) 8.474E-07 J
- d) 9.321E-07 J
- e) 1.025E-06 J

- a) 2.573E+01 J
- b) 2.831E+01 J
- c) 3.114E+01 J
- d) 3.425E+01 J
- e) 3.768E+01 J
41) A 12.0 V battery can move 9,000 C of charge. How many Joules does it deliver?
- a) 8.114E+04 J
- b) 8.926E+04 J
- c) 9.818E+04 J
- d) 1.080E+05 J
- e) 1.188E+05 J
42) When a 7.85 V battery operates a 1.82 W bulb, how many electrons pass through it each second?
- a) 1.087E+18 electrons
- b) 1.196E+18 electrons
- c) 1.316E+18 electrons
- d) 1.447E+18 electrons
- e) 1.592E+18 electrons
43) Calculate the final speed of a free electron accelerated from rest through a potential difference of 3 V.
- a) 9.339E+05 m/s
- b) 1.027E+06 m/s
- c) 1.130E+06 m/s
- d) 1.243E+06 m/s
- e) 1.367E+06 m/s

- a) 9.885E-01 N
- b) 1.087E+00 N
- c) 1.196E+00 N
- d) 1.316E+00 N
- e) 1.447E+00 N
45) Assume that a 21 nC charge is situated at the origin. Calculate the the magnitude (absolute value) of the potential difference between points P1 and P2 where the polar coordinates (r,φ) of P1 are (5 cm, 0°) and P2 is at (16 cm, 51°).
- a) 2.145E+03 V
- b) 2.359E+03 V
- c) 2.595E+03 V
- d) 2.855E+03 V
- e) 3.140E+03 V

- a) 9.627E+00 μC
- b) 1.059E+01 μC
- c) 1.165E+01 μC
- d) 1.281E+01 μC
- e) 1.409E+01 μC

- a) 6.901E+02 V
- b) 7.591E+02 V
- c) 8.350E+02 V
- d) 9.185E+02 V
- e) 1.010E+03 V
48) If a 22 nC charge is situated at the origin, the equipotential surface for V(x,y,z)=16 V is x2 + y2 + z2 = R2, where R=
- a) 8.441E+00 m
- b) 9.285E+00 m
- c) 1.021E+01 m
- d) 1.123E+01 m
- e) 1.236E+01 m
49) Two large parallel conducting plates are separated by 7.57 mm. Equal and opposite surface charges of 7.830E-07 C/m2 exist on the surfaces between the plates. What is the distance between equipotential planes which differ by 57 V?
- a) 6.446E-01 mm
- b) 7.412E-01 mm
- c) 8.524E-01 mm
- d) 9.803E-01 mm
- e) 1.127E+00 mm
50) An empty parallel-plate capacitor with metal plates has an area of 1.89 m2, separated by 1.36 mm. How much charge does it store if the voltage is 4.040E+03 V?
- a) 3.395E+01 μC
- b) 3.735E+01 μC
- c) 4.108E+01 μC
- d) 4.519E+01 μC
- e) 4.971E+01 μC

- a) 3.515E+00 μF
- b) 3.867E+00 μF
- c) 4.254E+00 μF
- d) 4.679E+00 μF
- e) 5.147E+00 μF

- a) 2.707E+01 μC
- b) 2.978E+01 μC
- c) 3.275E+01 μC
- d) 3.603E+01 μC
- e) 3.963E+01 μC

- a) 8.800E+00 μJ
- b) 9.680E+00 μJ
- c) 1.065E+01 μJ
- d) 1.171E+01 μJ
- e) 1.288E+01 μJ
54) A parallel plate capacitor has both plates with an area of 1.25 m2. The separation between the plates is 0.83mm. Applied to the plates is a potential difference of 4.65 kV. What is the capacitance?
- a) 8.77 nF.
- b) 10.08 nF.
- c) 11.6 nF.
- d) 13.33 nF.
- e) 15.33 nF.
55) The same parallel plate capacitor, with area 1.25 m2, plate separation 0.83mm, and an applied voltage of 4.65 kV. How much charge is stored?
- a) 35.45 μC.
- b) 40.77 μC.
- c) 46.89 μC.
- d) 53.92 μC.
- e) 62.01 μC.
56) A 0.6 Farad capacitor is charged with 1.5 Coulombs. What is the value of the electric field if the plates are 0.8 mm apart?
- a) 3.13 kV/m.
- b) 3.59 kV/m.
- c) 4.13 kV/m.
- d) 4.75 kV/m.
- e) 5.47 kV/m.
57) A 0.6 Farad capacitor charged with 1.5 Coulombs. What is the energy stored in the capacitor if the plates are 0.8 mm apart?
- a) 1.07 J.
- b) 1.23 J.
- c) 1.42 J.
- d) 1.63 J.
- e) 1.88 J.
58) A 0.6 Farad capacitor charged with 1.5 Coulombs. What is the force between the plates if they are 0.8 mm apart?
- a) 1772 N.
- b) 2038 N.
- c) 2344 N.
- d) 2695 N.
- e) 3100 N.
59) How fast is a 2212 eV electron moving?
- a) 8.3 x 106 m/s.
- b) 1.2 x 107 m/s.
- c) 1.9 x 107 m/s.
- d) 2.8 x 107 m/s.
- e) 4.2 x 107 m/s.
60) A proton is accelerated (at rest) from a plate held at 552.1 volts to a plate at zero volts. What is the final speed?
- a) 3.3 x 105 m/s.
- b) 4.9 x 105 m/s.
- c) 7.3 x 105 m/s.
- d) 1.1 x 106 m/s.
- e) 1.6 x 106 m/s.
61) What voltage is required accelerate an electron at rest to a speed of 9.7 x 104 m/s?
- a) 1.8 x 10-2 volts
- b) 2.7 x 10-2 volts
- c) 4 x 10-2 volts
- d) 6 x 10-2 volts
- e) 9 x 10-2 volts
62) What voltage is required to stop a proton moving at a speed of 3 x 104 m/s?
- a) 1.4 x 100 volts
- b) 2.1 x 100 volts
- c) 3.1 x 100 volts
- d) 4.7 x 100 volts
- e) 7 x 100 volts
63) What is the average current involved when a truck battery sets in motion 702 C of charge in 2.92 s while starting an engine?
- a) 2.404E+02 A
- b) 2.645E+02 A
- c) 2.909E+02 A
- d) 3.200E+02 A
- e) 3.520E+02 A
64) The charge passing a plane intersecting a wire is , where =38 C and 0.0106 s. What is the current at 0.0123 s?
- a) 1.021E+03 A
- b) 1.123E+03 A
- c) 1.236E+03 A
- d) 1.359E+03 A
- e) 1.495E+03 A
65) Calculate the drift speed of electrons in a copper wire with a diameter of 3.32 mm carrying a 18.4 A current, given that there is one free electron per copper atom. The density of copper is 8.80 x 103kg/m3 and the atomic mass of copper is 63.54 g/mol. Avagadro's number is 6.02 x 1023atoms/mol.
- a) 1.195E-04 m/s
- b) 1.315E-04 m/s
- c) 1.446E-04 m/s
- d) 1.591E-04 m/s
- e) 1.750E-04 m/s
66) A make-believe metal has a density of 5.880E+03 kg/m3 and an atomic mass of 73.2 g/mol. Taking Avogadro's number to be 6.020E+23 atoms/mol and assuming one free electron per atom, calculate the number of free electrons per cubic meter.
- a) 4.396E+28 e−/m3
- b) 4.836E+28 e−/m3
- c) 5.319E+28 e−/m3
- d) 5.851E+28 e−/m3
- e) 6.436E+28 e−/m3
67) A device requires consumes 121 W of power and requires 5.12 A of current which is supplied by a single core 10-guage (2.588 mm diameter) wire. Find the magnitude of the average current density.
- a) 8.849E+05 A/m2
- b) 9.734E+05 A/m2
- c) 1.071E+06 A/m2
- d) 1.178E+06 A/m2
- e) 1.296E+06 A/m2
68) Calculate the resistance of a 12-gauge copper wire that is 97 m long and carries a current of 29 mA. The resistivity of copper is 1.680E-08 Ω·m and 12-gauge wire as a cross-sectional area of 3.31 mm2.
- a) 4.923E-01 Ω
- b) 5.416E-01 Ω
- c) 5.957E-01 Ω
- d) 6.553E-01 Ω
- e) 7.208E-01 Ω
69) Calculate the electric field in a 12-gauge copper wire that is 75 m long and carries a current of 21 mA. The resistivity of copper is 1.680E-08 Ω·m and 12-gauge wire as a cross-sectional area of 3.31 mm2.
- a) 7.280E-05 V/m
- b) 8.008E-05 V/m
- c) 8.809E-05 V/m
- d) 9.690E-05 V/m
- e) 1.066E-04 V/m
70) Imagine a substance could be made into a very hot filament. Suppose the resitance is 2.14 Ω at a temperature of 77°C and that the temperature coefficient of expansion is 4.750E-03 (°C)−1). What is the resistance at a temperature of 542 °C?
- a) 6.540E+00 Ω
- b) 6.867E+00 Ω
- c) 7.210E+00 Ω
- d) 7.571E+00 Ω
- e) 7.949E+00 Ω
71) A DC winch moter draws 31 amps at 191 volts as it lifts a 5.080E+03 N weight at a constant speed of 0.99 m/s. Assuming that all the electrical power is either converted into gravitational potential energy or ohmically heats the motor's coils, calculate the coil's resistance.
- a) 6.972E-01 Ω
- b) 7.669E-01 Ω
- c) 8.436E-01 Ω
- d) 9.280E-01 Ω
- e) 1.021E+00 Ω
72) What is consumer cost to operate one 77−W incandescent bulb for 12 hours per day for 1 year (365 days) if the cost of electricity is $0.134 per kilowatt-hour?
- a) $3.087E+01
- b) $3.395E+01
- c) $3.735E+01
- d) $4.108E+01
- e) $4.519E+01
73) A given battery has a 12 V emf and an internal resistance of 0.193 Ω. If it is connected to a 0.89 Ω resistor what is the power dissipated by that load?
- a) 8.210E+01 W
- b) 9.030E+01 W
- c) 9.934E+01 W
- d) 1.093E+02 W
- e) 1.202E+02 W
74) A battery with a terminal voltage of 14.9 V is connected to a circuit consisting of 2 23.3 Ω resistors and one 13.6 Ω resistor. What is the voltage drop across the 13.6 Ω resistor?
- a) 3.366E+00 V
- b) 3.703E+00 V
- c) 4.073E+00 V
- d) 4.480E+00 V
- e) 4.928E+00 V
75) Three resistors, R1 = 1.7 Ω, and R2 = R2 = 3.75 Ω, are connected in parallel to a 9.74 V voltage source. Calculate the power dissipated by the smaller resistor (R1.)
- a) 4.193E+01 W
- b) 4.612E+01 W
- c) 5.073E+01 W
- d) 5.580E+01 W
- e) 6.138E+01 W

- a) 2.993E+01 W
- b) 3.293E+01 W
- c) 3.622E+01 W
- d) 3.984E+01 W
- e) 4.383E+01 W

- a) 8.841E-02 A
- b) 9.725E-02 A
- c) 1.070E-01 A
- d) 1.177E-01 A
- e) 1.294E-01 A

- a) 1.726E+00 mA
- b) 1.898E+00 mA
- c) 2.088E+00 mA
- d) 2.297E+00 mA
- e) 2.527E+00 mA

- a) 1.276E+01 V
- b) 1.404E+01 V
- c) 1.544E+01 V
- d) 1.699E+01 V
- e) 1.869E+01 V

- a) 1.981E+01 V
- b) 2.180E+01 V
- c) 2.398E+01 V
- d) 2.637E+01 V
- e) 2.901E+01 V

- a) 1.084E+01 s
- b) 1.192E+01 s
- c) 1.311E+01 s
- d) 1.442E+01 s
- e) 1.586E+01 s
82) A 5.3 volt battery moves 11 Coulombs of charge in 2.1 hours. What is the power?
- a) 7.71 x 10-3 W
- b) 9.34 x 10-3 W
- c) 1.13 x 10-2 W
- d) 1.37 x 10-2 W
- e) 1.66 x 10-2 W
83) The diameter of a copper wire is 1.7 mm, and it carries a current of 92 amps. What is the drift velocity if copper has a density of 8.8E3 kg/m3 and an atomic mass of 63.54 g/mol? (1 mol = 6.02E23 atoms, and copper has one free electron per atom.)
- a) 2.07 x 10-3m/s
- b) 2.5 x 10-3m/s
- c) 3.03 x 10-3m/s
- d) 3.67 x 10-3m/s
- e) 4.45 x 10-3m/s
84) A 164 Watt DC motor draws 0.25 amps of current. What is effective resistance?
- a) 1.22 x 103 Ω
- b) 1.48 x 103 Ω
- c) 1.79 x 103 Ω
- d) 2.17 x 103 Ω
- e) 2.62 x 103 Ω
85) A power supply delivers 149 watts of power to a 153 ohm resistor. What was the applied voltage?
- a) 8.49 x 101 volts
- b) 1.03 x 102 volts
- c) 1.25 x 102 volts
- d) 1.51 x 102 volts
- e) 1.83 x 102 volts
86) 3 amps flow through a 1 Ohm resistor. What is the voltage?
- a)
- b)
- c)
- d) None these are correct.
87) A 1 ohm resistor has 5 volts DC across its terminals. What is the current (I) and the power consumed?
- a) I = 5A & P = 3W.
- b) I = 5A & P = 5W.
- c) I = 5A & P = 25W.
- d) I = 5A & P = 9W
88) The voltage across two resistors in series is 10 volts. One resistor is twice as large as the other. What is the voltage across the larger resistor? What is the voltage across the smaller one?
- a) and.
- b) and .
- c) and .
- d) None of these are true.
89) A 1 ohm, 2 ohm, and 3 ohm resistor are connected in series. What is the total resistance?
- a) .
- b) .
- c) .
- d) None of these are true.
90) Two identical resistors are connected in series. The voltage across both of them is 250 volts. What is the voltage across each one?
- a) and .
- b) None of these are true.
- c) and .
- d) and .
91) A 1 ohm, 2 ohm, and 3 ohm resistor are connected in parallel. What is the total resistance?
- a) .
- b) .
- c) .
- d) .
92) A 5 ohm and a 2 ohm resistor are connected in parallel. What is the total resistance?
- a) .
- b) .
- c) .
- d) .
93) A 7 ohm and a 3 ohm resistor are connected in parallel. What is the total resistance?
- a) .
- b) .
- c) .
- d) .
94) Three 1 ohm resistors are connected in parallel. What is the total resistance?
- a) .
- b) .
- c) .
- d) .
95) If you put an infinite number of resistors in parallel, what would the total resistance be?
- a) would approach Zero as The No. of Resistors In parallel Approaches Infinity.
- b) None of these are true.
- c) would approach 1 as The No. of Resistors In parallel Approaches Infinity
- d) It is not possible to connect that Number of Resistors in parallel.
97) Why do we say the "voltage across" or "the voltage with respect to?" Why can't we just say voltage?
- a) It's an Electrical Cliche.
- b) The other point could be Negative or positive.
- c) None these are correct
- d) Voltage is a measure of Electric Potential difference between two electrical points.
- a) ; ; ; ..
- b) ; ; ; .
- c) ; ; ; .
- d) ; ; ; .
99) Two resistors are in parallel with a voltage source. How do their voltages compare?
- a) The voltage across both resistors is the same as the source.
- b) None of these are true.
- c) One has full voltage, the other has none.
- d) The voltage across both resistors is half the voltage of the source.
100) A resistor consumes 5 watts, and its current is 10 amps. What is its voltage?
- a) 2V.
- b) 10V.
- c) 0.5V.
- d) 15V.
101) A resistor has 10 volts across it and 4 amps going through it. What is its resistance?
- a) None of these are true.
- b)
- c)
- d)
102) If you plot voltage vs. current in a circuit, and you get a linear line, what is the significance of the slope?
- a) Power.
- b) Resistance.
- c) Discriminant.
- d) None of these are true.
103) A resistor has 3 volts across it. Its resistance is 1.5 ohms. What is the current?
- a) 12A
- b) 3A
- c) 2A
- d) 1.5A
104) A resistor has 8 volts across it and 3 Amps going through it. What is the power consumed?
- a) 2.2W
- b) 24W
- c) 8W
- d) 3W
105) A resistor has a voltage of 5 volts and a resistance of 15 ohms. What is the power consumed?
- a) None of these are ture.
- b) 11.67 Joules
- c) 1.67 Watts
- d) 2.5 Watts
106) A resistor is on for 5 seconds. It consumes power at a rate of 5 watts. How many joules are used?
- a) 25 Joules
- b) 3 Joules
- c) 5 Joules
- d) None of these are true
107) An ideal 6.1 V voltage source is connected to two resistors in parallel. One is 2.4, and the other is 4.2 . What is the current through the larger resistor?
- a) 0.61 mA.
- b) 0.7 mA.
- c) 0.8 mA.
- d) 0.92 mA.
- e) 1.06 mA.
108) A 6 ohm resistor is connected in series to a pair of 5 ohm resistors that are in parallel. What is the net resistance?
- a) 7.4 ohms.
- b) 8.5 ohms.
- c) 9.8 ohms.
- d) 11.2 ohms.
- e) 12.9 ohms.
109) Two 8.8 ohm resistors are connected in parallel. This combination is then connected in series to a 2.8 ohm resistor. What is the net resistance?
- a) 6.3 ohms.
- b) 7.2 ohms.
- c) 8.3 ohms.
- d) 9.5 ohms.
- e) 11 ohms.
110) An ideal 6 volt battery is connected to a 0.073 ohm resistor. To measure the current an ammeter with a resistance of 14 is used. What current does the ammeter actually read?
- a) 60 A.
- b) 69 A.
- c) 79.3 A.
- d) 91.2 A.
- e) 104.9 A.
111) A battery has an emf of 6.1 volts, and an internal resistance of 366 . It is connected to a 3.6 resistor. What power is developed in the 3.6 resistor?
- a) 6.44 W.
- b) 7.41 W.
- c) 8.52 W.
- d) 9.79 W.
- e) 11.26 W.
112) An alpha-particle (q=3.2x10−19C) moves through a uniform magnetic field that is parallel to the positive z-axis with magnitude 5.11 T. What is the x-component of the force on the alpha-particle if it is moving with a velocity
(8.99 i + 7.56 j + 8.49 k) x 104 m/s?
- a) 1.124E-13 N
- b) 1.236E-13 N
- c) 1.360E-13 N
- d) 1.496E-13 N
- e) 1.645E-13 N
113) A charged particle in a magnetic field of 2.780E-04 T is moving perpendicular to the magnetic field with a speed of 6.370E+05 m/s. What is the period of orbit if orbital radius is 0.671 m?
- a) 6.017E-06 s
- b) 6.619E-06 s
- c) 7.280E-06 s
- d) 8.008E-06 s
- e) 8.809E-06 s
114) An alpha-particle (m=6.64x10−27kg, q=3.2x10−19C) briefly enters a uniform magnetic field of magnitude 0.0783 T . It emerges after being deflected by 64° from its original direction. How much time did it spend in that magnetic field?
- a) 2.224E-07 s
- b) 2.446E-07 s
- c) 2.691E-07 s
- d) 2.960E-07 s
- e) 3.256E-07 s
115) A 18 cm-long horizontal wire is maintained in static equilibrium by a horizontally directed magnetic field that is perpendicular to the wire (and to Earth's gravity). The mass of the wire is 8 g, and the magnitude of the magnetic field is 0.351 T. What current is required to maintain this balance?
- a) 1.241E+00 A
- b) 1.365E+00 A
- c) 1.501E+00 A
- d) 1.652E+00 A
- e) 1.817E+00 A
116) A long rigid wire carries a 8 A current. What is the magnetic force per unit length on the wire if a 0.899 T magnetic field is directed 43° away from the wire?
- a) 3.685E+00 N/m
- b) 4.054E+00 N/m
- c) 4.459E+00 N/m
- d) 4.905E+00 N/m
- e) 5.395E+00 N/m
117) A circular current loop of radius 2.86 cm carries a current of 1.7 mA. What is the magnitude of the torque if the dipole is oriented at 43 ° to a uniform magnetic fied of 0.729 T?
- a) 1.483E-06 N m
- b) 1.632E-06 N m
- c) 1.795E-06 N m
- d) 1.974E-06 N m
- e) 2.172E-06 N m
118) An electron beam (m=9.1 x 10−31kg, q=1.6 x 10−19C) enters a crossed-field velocity selector with magnetic and electric fields of 5.53 mT and 7.210E+03 N/C, respectively. What must the velocity of the electron beam be to transverse the crossed fields undeflected ?
- a) 8.905E+05 m/s
- b) 9.796E+05 m/s
- c) 1.078E+06 m/s
- d) 1.185E+06 m/s
- e) 1.304E+06 m/s

- a) 1.255E-06 V
- b) 1.380E-06 V
- c) 1.518E-06 V
- d) 1.670E-06 V
- e) 1.837E-06 V
120) A cyclotron used to accelerate alpha particlesm=6.64 x 10−27kg, q=3.2 x 10−19C) has a radius of 0.398 m and a magneticfield of 0.855 T. What is their maximum kinetic energy?
- a) 5.581E+00 MeV
- b) 6.139E+00 MeV
- c) 6.753E+00 MeV
- d) 7.428E+00 MeV
- e) 8.171E+00 MeV
121) A wire carries a current of 316 A in a circular arc with radius 1.55 cm swept through 76 degrees. Assuming that the rest of the current is 100% shielded by mu-metal, what is the magnetic field at the center of the arc?
- a) 8.070E+00 Tesla
- b) 8.878E+00 Tesla
- c) 9.765E+00 Tesla
- d) 1.074E+01 Tesla
- e) 1.182E+01 Tesla

- a) Bx= 4.887E-05 T
- b) Bx= 5.376E-05 T
- c) Bx= 5.914E-05 T
- d) Bx= 6.505E-05 T
- e) Bx= 7.156E-05 T

- a) By= 5.510E-05 T
- b) By= 6.061E-05 T
- c) By= 6.667E-05 T
- d) By= 7.333E-05 T
- e) By= 8.067E-05 T
124) Two parallel wires each carry a 5.0 mA current and are oriented in the z direction. The first wire is located in the x-y plane at (4.48 cm, 0.973 cm), while the other is located at (3.32 cm, 4.79 cm). What is the force per unit length between the wires?
- a) 1.139E-10 N/m
- b) 1.253E-10 N/m
- c) 1.379E-10 N/m
- d) 1.517E-10 N/m
- e) 1.668E-10 N/m
125) Two loops of wire carry the same current of 62 kA, and flow in the same direction. They share a common axis and orientation. One loop has a radius of 0.584 m while the other has a radius of 1.38 m. What is the magnitude of the magnetic field at a point on the axis of both loops, situated between the loops at a distance 0.341 m from the first (smaller) loopif the disance between the loops is 1.21 m?
- a) 4.102E-02 T
- b) 4.513E-02 T
- c) 4.964E-02 T
- d) 5.460E-02 T
- e) 6.006E-02 T
126) Under most conditions the current is distributed uniformly over the cross section of the wire. What is the magnetic field 1.34 mm from the center of a wire of radius 3 mm if the current is 1A?
- a) 2.237E-05 T
- b) 2.461E-05 T
- c) 2.707E-05 T
- d) 2.978E-05 T
- e) 3.276E-05 T
127) The Z-pinch is an (often unstable) cylindrical plasma in which a aximuthal magnetic field is produced by a current in the z direction. A simple model for the magnetic field, valid for is,
,
where is the maximum magnetic field (at ). If 0.703 m and 0.521 T, then how much current (in the z-direction) flows through a circle of radius 0.165 m that is centered on the axis with its plane perpendicular to the axis?
- a) 1.338E+05 A
- b) 1.472E+05 A
- c) 1.619E+05 A
- d) 1.781E+05 A
- e) 1.959E+05 A

:
- a) 1.547E-03 T-m
- b) 1.702E-03 T-m
- c) 1.872E-03 T-m
- d) 2.060E-03 T-m
- e) 2.266E-03 T-m

:
- a) 4.069E-03 T-m
- b) 4.476E-03 T-m
- c) 4.924E-03 T-m
- d) 5.416E-03 T-m
- e) 5.958E-03 T-m
130) A solenoid has 8.230E+04 turns wound around a cylinder of diameter 1.5 cm and length 18 m. The current through the coils is 0.633 A. Define the origin to be the center of the solenoid and neglect end effects as you calculate the line integral alongthe axis from z=−3.74 cm to z=+3.23 cm
- a) 1.731E-04 T-m
- b) 1.905E-04 T-m
- c) 2.095E-04 T-m
- d) 2.305E-04 T-m
- e) 2.535E-04 T-m
131) A long coil is tightly wound around a (hypothetical) ferromagnetic cylinder. If n= 20 turns per centimeter and the current applied to the solenoid is 598 mA, the net magnetic field is measured to be 1.38 T. What is the magnetic susceptibility for this case?
- a) 8.338E+02
- b) 9.172E+02
- c) 1.009E+03
- d) 1.110E+03
- e) 1.221E+03
132) A cosmic ray alpha particle encounters Earth's magnetic field at right angles to a field of 11.4 μT. The kinetic energy is 307 keV. What is the radius of particle's orbit?
- a) 7 x 101 m.
- b) 2.2 x 102 m.
- c) 7 x 102 m.
- d) 2.2 x 103 m.
- e) 7 x 103 m.
133) Two parallel wires are 6.7 meters long, and are separated by 5.7 mm. What is the force if both wires carry a current of 13.3 amps?
- a) 4.16 x 10-4 newtons
- b) 1.32 x 10-3 newtons
- c) 4.16 x 10-3 newtons
- d) 1.32 x 10-2 newtons
- e) 4.16 x 10-2 newtons
134) Blood is flowing at an average rate of 20.5 cm/s in an artery that has an inner diameter of 4.5 mm. What is the voltage across a hall probe placed across the inner diameter of the artery if the perpendicular magnetic field is 0.12 Tesla?
- a) 3.5 x 10-5 Volts
- b) 1.11 x 10-4 Volts
- c) 3.5 x 10-4 Volts
- d) 1.11 x 10-3 Volts
- e) 3.5 x 10-3 Volts
135) An electron tube on Earth's surface is oriented horizontally towards magnetic north. The electron is traveling at 0.07c, and Earth's magnetic field makes an angle of 47.5 degrees with respect to the horizontal. To counter the magnetic force, a voltage is applied between two large parallel plates that are 57 mm apart. What must be the applied voltage if the magnetic field is 46μT?
- a) 4.1 x 100 volts
- b) 1.3 x 101 volts
- c) 4.1 x 101 volts
- d) 1.3 x 102 volts
- e) 4.1 x 102 volts
136) Amphere's law for magnetostatic currents is that equals the current enclosed by the closed loop, and is the magnetic field. A current of 8.2A flows upward along the z axis. Noting that for this geometry, , calculate the line integral for a circle of radius 9.6m.
- a) 6.03E+01 m
- b) 6.61E+01 m
- c) 7.25E+01 m
- d) 7.95E+01 m
- e) 8.72E+01 m
137) If , where is magnetic field, what is at a distance of 9.6m from a wire carrying a current of 8.2A?
- a) 1.24E-01 A/m
- b) 1.36E-01 A/m
- c) 1.49E-01 A/m
- d) 1.63E-01 A/m
- e) 1.79E-01 A/m
138) If , where is magnetic field, what is at the point (8.6443,4.1757) if a current of 8.2A flows through a wire that runs along the z axis?
- a) 8.47E-02 A/m
- b) 9.29E-02 A/m
- c) 1.02E-01 A/m
- d) 1.12E-01 A/m
- e) 1.22E-01 A/m
139) A very long and thin solenoid has 2705 turns and is 134 meters long. The wire carrys a current of 8.2A. What is the magnetic field in the center?
- a) 1.90E-04 Tesla
- b) 2.08E-04 Tesla
- c) 2.28E-04 Tesla
- d) 2.50E-04 Tesla
- e) 2.74E-04 Tesla
140) A very long and thin solenoid has 1223 turns and is 134 meters long. The wire carrys a current of 8.2A. If this solenoid is sufficiently thin, what is the line integral of along an on-axis path that starts 28 meters from the center and stops 93 meters from the center?
- a) 2.21E+03 A
- b) 2.43E+03 A
- c) 2.66E+03 A
- d) 2.92E+03 A
- e) 3.20E+03 A
141) What is the sum of 5.2 apples plus 76 apples?
- a) 7.41E+01 apples
- b) 8.12E+01 apples
- c) 8.90E+01 apples
- d) 9.76E+01 apples
- e) 1.07E+02 apples
142) H is defined by, B=μ0H, where B is magnetic field. A current of 52A passes along the z-axis. Use symmetry to find the integral, , from the point (0,7.5) to the point (7.5,0).
- a) 1.19E+01 amps
- b) 1.30E+01 amps
- c) 1.43E+01 amps
- d) 1.56E+01 amps
- e) 1.71E+01 amps
143) H is defined by, B=μ0H, where B is magnetic field. A current of 96A passes along the z-axis. Use symmetry to find the integral, , from the point (-6.6, 6.6) to the point (6.6, 6.6).
- a) 1.82E+01 amps
- b) 2.00E+01 amps
- c) 2.19E+01 amps
- d) 2.40E+01 amps
- e) 2.63E+01 amps
144) H is defined by, B=μ0H, where B is magnetic field. A current of 33A passes along the z-axis. Use symmetry to find the integral, , from the point (0,9.5) to the point (9.5,9.5).
- a) 3.43E+00 amps
- b) 3.76E+00 amps
- c) 4.13E+00 amps
- d) 4.52E+00 amps
- e) 4.96E+00 amps
145) H is defined by, B=μ0H, where B is magnetic field. A current of 94A passes along the z-axis. Use symmetry to find the integral, , from (-∞,6.2) to (+∞,6.2).
- a) 3.91E+01 amps
- b) 4.29E+01 amps
- c) 4.70E+01 amps
- d) 5.15E+01 amps
- e) 5.65E+01 amps
146) A square coil has sides that are L= 0.673 m long and is tightly wound with N=211 turns of wire. The resistance of the coil is R=5.31 Ω. The coil is placed in a spacially uniform magnetic field that is directed perpendicular to the face of the coil and whose magnitude is increasing at a rate dB/dt=0.0454 T/s. If R represents the only impedance of the coil, what is the magnitude of the current circulting through it?
- a) 6.753E-01 A
- b) 7.428E-01 A
- c) 8.171E-01 A
- d) 8.988E-01 A
- e) 9.887E-01 A
147) A time dependent magnetic field is directed perpendicular to the plane of a circular coil with a radius of 0.317 m. The magnetic field is spatially uniform but decays in time according to , where 6.25 s. What is the current in the coil if the impedance of the coil is 52.3 Ω?
- a) 6.717E-02 A
- b) 7.388E-02 A
- c) 8.127E-02 A
- d) 8.940E-02 A
- e) 9.834E-02 A
148) The current through the windings of a solenoid with n= 2.120E+03 turns per meter is changing at a rate dI/dt=4 A/s. The solenoid is 94 cm long and has a cross-sectional diameter of 2.56 cm. A small coil consisting of N=30turns wraped in a circle of diameter 1.15 cm is placed in the middle of the solenoid such that the plane of the coil is perpendicular to the central axis of the solenoid. Assume that the infinite-solenoid approximation is valid inside the small coil. What is the emf induced in the coil?
- a) 3.019E-05 V
- b) 3.321E-05 V
- c) 3.653E-05 V
- d) 4.018E-05 V
- e) 4.420E-05 V
149) Calculate the motional emf induced along a 40.1 km conductor moving at an orbital speed of 7.85 km/s perpendicular to Earth's 5.160E-05 Tesla magnetic field.
- a) 1.477E+04 V
- b) 1.624E+04 V
- c) 1.787E+04 V
- d) 1.965E+04 V
- e) 2.162E+04 V

--(Answer & Why this question is different.)
- a) 6.980E+00 cm3/s
- b) 7.678E+00 cm3/s
- c) 8.446E+00 cm3/s
- d) 9.290E+00 cm3/s
- e) 1.022E+01 cm3/s
151) A recangular coil with an area of 0.371 m2 and 20 turns is placed in a uniform magnetic field of 2.51 T. The coil is rotated about an axis that is perpendicular to this field. At time t=0 the normal to the coil is oriented parallel to the magnetic field and the coil is rotating with a constant angular frequency of 3.060E+03 s−1. What is the magnitude (absolute value) of the induced emf at t = 88 s?
- a) 5.694E+04 V
- b) 6.263E+04 V
- c) 6.889E+04 V
- d) 7.578E+04 V
- e) 8.336E+04 V
152) A spatially uniform magnetic points in the z-direction and oscilates with time as where 3.26 T and 9.250E+03 s−1. Suppose the electric field is always zero at point , and consider a circle of radius 0.385 m that is centered at that point and oriented in a plane perpendicular to the magnetic field. Evaluate the maximum value of the line integral around the circle.
- a) 6.029E+04 V
- b) 6.631E+04 V
- c) 7.295E+04 V
- d) 8.024E+04 V
- e) 8.826E+04 V
153) A long solenoid has a radius of 0.442 m and 63 turns per meter; its current decreases with time according to , where 7 A and 22 s−1.What is the induced electric fied at a distance 1.94 m from the axis at time t=0.0331 s ?
- a) 2.964E-04 V/m
- b) 3.260E-04 V/m
- c) 3.586E-04 V/m
- d) 3.945E-04 V/m
- e) 4.339E-04 V/m
154) A long solenoid has a radius of 0.508 m and 90 turns per meter; its current decreases with time according to , where 7 A and 25 s−1.What is the induced electric fied at a distance 0.145 m from the axis at time t=0.0643 s ?
- a) 2.614E-04 V/m
- b) 2.875E-04 V/m
- c) 3.163E-04 V/m
- d) 3.479E-04 V/m
- e) 3.827E-04 V/m
- a) 6.667E-02 V
- b) 7.334E-02 V
- c) 8.067E-02 V
- d) 8.874E-02 V
- e) 9.762E-02 V
156) An induced emf of 4.82V is measured across a coil of 73 closely wound turns while the current throuth it increases uniformly from 0.0 to 4.61A in 0.934s. What is the self-inductance of the coil?
- a) 7.337E-01 H
- b) 8.071E-01 H
- c) 8.878E-01 H
- d) 9.765E-01 H
- e) 1.074E+00 H
157) A washer has an inner diameter of 2.57 cm and an outer diamter of 4.14 cm. The thickness is where is measured in cm, , and . What is the volume of the washer?
- a) 7.226E-01 cm3
- b) 7.949E-01 cm3
- c) 8.744E-01 cm3
- d) 9.618E-01 cm3
- e) 1.058E+00 cm3

- a) 4.109E-01 V
- b) 4.930E-01 V
- c) 5.917E-01 V
- d) 7.100E-01 V
- e) 8.520E-01 V

- a) -1.442E+00 s
- b) -1.586E+00 s
- c) -1.744E+00 s
- d) -1.919E+00 s
- e) -2.111E+00 s
160) In an LC circuit, the self-inductance is 0.0134 H and the capacitance is 3.280E-06 F. At t=0 all the energy is stored in the capacitor, which has a charge of 5.930E-05 C. How long does it take for the capacitor to become completely discharged?
- a) 2.722E-04 s
- b) 2.994E-04 s
- c) 3.293E-04 s
- d) 3.622E-04 s
- e) 3.985E-04 s
161) An ac generator produces an emf of amplitude 78 V at a frequency of 45 Hz. What is the maximum amplitude of the current if the generator is connected to a 60 mF inductor?
- a) 3.140E+00 A
- b) 3.454E+00 A
- c) 3.800E+00 A
- d) 4.180E+00 A
- e) 4.598E+00 A
162) An ac generator produces an emf of amplitude 64 V at a frequency of 95 Hz. What is the maximum amplitude of the current if the generator is connected to a 99 mF capacitor?
- a) 3.126E+00 A
- b) 3.438E+00 A
- c) 3.782E+00 A
- d) 4.160E+00 A
- e) 4.576E+00 A
163) The output of an ac generator connected to an RLC series combination has a frequency of 510 Hz and an amplitude of 0.69 V;. If R =4 Ω, L= 4.30E-03H , and C=9.20E-04 F, what is the impedance?
- a) 1.054E+01 Ω
- b) 1.159E+01 Ω
- c) 1.275E+01 Ω
- d) 1.402E+01 Ω
- e) 1.542E+01 Ω
164) The output of an ac generator connected to an RLC series combination has a frequency of 480 Hz and an amplitude of 0.17 V;. If R =5 Ω, L= 6.70E-03H , and C=6.30E-04 F, what is the magnitude (absolute value) of the phase difference between current and emf?
- a) 1.322E+00 &rad;
- b) 1.454E+00 &rad;
- c) 1.600E+00 &rad;
- d) 1.760E+00 &rad;
- e) 1.936E+00 &rad;
165) The output of an ac generator connected to an RLC series combination has a frequency of 8.20E+04 Hz and an amplitude of 4 V. If R =5 Ω, L= 5.40E-03H , and C=9.80E-06 F, what is the rms power transferred to the resistor?
- a) 1.865E-04 Watts
- b) 2.051E-04 Watts
- c) 2.256E-04 Watts
- d) 2.482E-04 Watts
- e) 2.730E-04 Watts
166) An RLC series combination is driven with an applied voltage of of V=V0sin(ωt), where V0=0.38 V. The resistance, inductance, and capacitance are R =7 Ω, L= 4.10E-03H , and C=7.40E-04 F, respectively. What is the amplitude of the current?
- a) 4.486E-02 A
- b) 4.935E-02 A
- c) 5.429E-02 A
- d) 5.971E-02 A
- e) 6.569E-02 A
167) The quality factor Q is a dimensionless paramater involving the relative values of the magnitudes of the at three impedances (R, XL, XC). Since Q is calculatedat resonance, XL, XC and only twoimpedances are involved, Q=≡ω0L/R is definedso that Q is large if the resistance is low. Calculate the Q of an LRC series driven at resonance by an applied voltage of of V=V0sin(ωt), where V0=1 V. The resistance, inductance, and capacitance are R =0.21 Ω, L= 4.80E-03H , and C=3.60E-06 F, respectively.
- a) Q = 1.739E+02
- b) Q = 2.000E+02
- c) Q = 2.300E+02
- d) Q = 2.645E+02
- e) Q = 3.041E+02
168) A step-down transformer steps 19 kV down to 220 V. The high-voltage input is provided by a 250 Ω power line that carries 4 A of currentWhat is the output current (at the 220 V side ?)
- a) 2.595E+02 A
- b) 2.855E+02 A
- c) 3.140E+02 A
- d) 3.455E+02 A
- e) 3.800E+02 A
169) Two orbiting satellites are orbiting at a speed of 77 km/s perpendicular to a magnetic field of 56 μT. They are connected by a cable that is 31 km long. A voltmeter is attached between a satellite and one end of the cable. The voltmeter's internal impedance far exceeds the net resistance through the ionosphere that completes the circuit. What is the measured voltage?
- a) 1.1 x 105 volts.
- b) 1.34 x 105 volts.
- c) 1.62 x 105 volts.
- d) 1.96 x 105 volts.
- e) 2.38 x 105 volts.
170) An loop of wire with 26 turns has a radius of 0.26 meters, and is oriented with its axis parallel to a magetic field of 0.75 Tesla. What is the induced voltage if this field is reduced to 13% of its original value in 1.8 seconds?
- a) 2 x 100 volts
- b) 2.42 x 100 volts
- c) 2.94 x 100 volts
- d) 3.56 x 100 volts
- e) 4.31 x 100 volts
171) A 547 mF capacitor is connected in series to a 2 kΩ resistor. If the capacitor is discharged, how long does it take to fall by a factor of e4? (where e =2.7...)
- a) 1.38 x 103 s.
- b) 4.38 x 103 s.
- c) 1.38 x 104 s.
- d) 4.38 x 104 s.
- e) 1.38 x 105 s.
172) A 665 μF capacitor is connected in series to a 806 kΩ resistor. If the capacitor is discharged, how long does it take to fall by a factor of e2? (where e =2.7...)
- a) 3.39 x 101 s.
- b) 1.07 x 102 s.
- c) 3.39 x 102 s.
- d) 1.07 x 103 s.
- e) 3.39 x 103 s.
173) A 206 mF capacitor is connected in series to a 990 MΩ resistor. If the capacitor is discharged, how long does it take to fall by a factor of e4? (where e =2.7...)
- a) 8.16 x 108 s.
- b) 2.58 x 109 s.
- c) 8.16 x 109 s.
- d) 2.58 x 1010 s.
- e) 8.16 x 1010 s.
174) A 5 F capacitor is connected in series to a 8Ω resistor. If the capacitor is discharged, how long does it take to fall by a factor of e4? (where e =2.7...)
- a) 1.6 x 101 s.
- b) 5.06 x 101 s.
- c) 1.6 x 102 s.
- d) 5.06 x 102 s.
- e) 1.6 x 103 s.

- a) 3.876E+01 V
- b) 4.263E+01 V
- c) 4.690E+01 V
- d) 5.159E+01 V
- e) 5.674E+01 V

- a) 3.765E+03 V/m
- b) 4.142E+03 V/m
- c) 4.556E+03 V/m
- d) 5.012E+03 V/m
- e) 5.513E+03 V/m

- a) 7.089E-02 A
- b) 7.798E-02 A
- c) 8.578E-02 A
- d) 9.436E-02 A
- e) 1.038E-01 A
178) A 46 kW radio transmitter on Earth sends it signal to a satellite 140 km away. At what distance in the same direction would the signal have the same maximum field strength if the transmitter's output power were increased to 73 kW?
- a) 1.764E+02 km
- b) 1.940E+02 km
- c) 2.134E+02 km
- d) 2.347E+02 km
- e) 2.582E+02 km
179) What is the radiation pressure on an object that is 5.90E+11 m away from the sun and has cross-sectional area of 0.014 m2? The average power output of the Sun is 3.80E+26 W.
- a) 5.268E-07 N/m2
- b) 5.795E-07 N/m2
- c) 6.375E-07 N/m2
- d) 7.012E-07 N/m2
- e) 7.713E-07 N/m2
180) What is the radiation force on an object that is 5.20E+11 m away from the sun and has cross-sectional area of 0.04 m2? The average power output of the Sun is 3.80E+26 W.
- a) 2.242E-08 N
- b) 2.466E-08 N
- c) 2.713E-08 N
- d) 2.984E-08 N
- e) 3.283E-08 N
181) A circlular capactitor of radius 3.3 m has a gap of 16 mm, and a charge of 68 μC. What is the electric field between the plates?
- a) 1.26E+05 N/C (or V/m)
- b) 1.53E+05 N/C (or V/m)
- c) 1.85E+05 N/C (or V/m)
- d) 2.24E+05 N/C (or V/m)
- e) 2.72E+05 N/C (or V/m)
182) A circlular capactitor of radius 4.6 m has a gap of 12 mm, and a charge of 77 μC. Compute the surface integral over an inner face of the capacitor.
- a) 6.59E-11 Vs2m-1
- b) 7.99E-11 Vs2m-1
- c) 9.68E-11 Vs2m-1
- d) 1.17E-10 Vs2m-1
- e) 1.42E-10 Vs2m-1
183) A circlular capactitor of radius 4.6 m has a gap of 11 mm, and a charge of 60 μC. The capacitor is discharged through a 9 kΩ resistor. What is the decay time?
- a) 3.28E-04 s
- b) 3.97E-04 s
- c) 4.82E-04 s
- d) 5.83E-04 s
- e) 7.07E-04 s
184) A circlular capactitor of radius 4.1 m has a gap of 11 mm, and a charge of 66 μC. The capacitor is discharged through a 6 kΩ resistor. What is what is the maximum magnetic field at the edge of the capacitor? (There are two ways to do this; you should know both.)
- a) 6.33E-09 Tesla
- b) 7.96E-09 Tesla
- c) 1.00E-08 Tesla
- d) 1.26E-08 Tesla
- e) 1.59E-08 Tesla

- a) how a nearsighted person might see a distant object
- b) how a nearsighted person might see an object that is too close for comfort
- c) how a farsighted person might see an object that is too close for comfort
- d) how a farsighted person might see a distant object
- a) how a nearsighted person might see a distant object
- b) how a farsighted person might see a distant object
- c) how a farsighted person might see an object that is too close for comfort
- d) how a nearsighted person might see an object that is too close for comfort
187) In optics, normal means
- a) to the left of the optical axis
- b) parallel to the surface
- c) perpendicular to the surface
- d) to the right of the optical axis
188) The law of reflection applies to
- a) only light in a vacuum
- b) telescopes but not microscopes
- c) curved surfaces
- d) both flat and curved surfaces
- e) flat surfaces
189) When light passes from air to glass
- a) the frequency decreases
- b) the frequency increases
- c) it bends away from the normal
- d) it bends towards the normal
- e) it does not bend
190) When light passes from glass to air
- a) it does not bend
- b) the frequency decreases
- c) the frequency increases
- d) it bends towards the normal
- e) it bends away from the normal
191) An important principle that allows fiber optics to work is
- a) the invariance of the speed of light
- b) total internal reflection
- c) total external refraction
- d) partial internal absorption
- e) the Doppler shift
192) The focal point is where
- a) rays meet whenever they pass through a lens
- b) rays meet if they were parallel to the optical axis before striking a lens
- c) rays meet whenever they are forming an image
- d) rays meet if they are parallel to each other
- e) the center of the lens
193) An object is placed 8 cm to the left of a diverging lens with a focal length of 4.3 cm. How far is the image from the lens?
- a) 2.8 x 100 cm
- b) 4.97 x 100 cm
- c) 8.84 x 100 cm
- d) 1.57 x 101 cm
- e) 2.8 x 101 cm
194) An object is placed 4.15 cm to the left of a converging lens with a focal length of 3.6 cm. How far is the image from the lens?
- a) 8.59 x 100 cm
- b) 1.53 x 101 cm
- c) 2.72 x 101 cm
- d) 4.83 x 101 cm
- e) 8.59 x 101 cm
195) An object of height 0.54 cm is placed 131 cm behind a diverging lens with a focal length of 71 cm. What is the height of the image?
- a) 9.15 x 10-2 cm
- b) 1.1 x 10-1 cm
- c) 1.32 x 10-1 cm
- d) 1.58 x 10-1 cm
- e) 1.9 x 10-1 cm
196) An object is placed 13.2 cm to the left of a diverging lens with a focal length of 17.1 cm. On the side, at a distance of 5.1 cm from the diverging lens is a converging lens with focal length equal to 4 cm. How far is the final image from the converging lens?
- a) 1.86 x 10-1 cm
- b) 5.87 x 10-1 cm
- c) 1.86 x 100 cm
- d) 5.87 x 100 cm
- e) 1.86 x 101 cm
198) ![]() If this represents the eye looking at an object, where is this object?
If this represents the eye looking at an object, where is this object?
- a) One focal length in front of the eye
- b) Two (of the other answers) are true
- c) very far away
- d) at infinity
- e) directly in front of the eye (almost touching)
199) After passing through a the lens of a camera or the eye, the focal point is defined as where the rays meet.
- a) true
- b) false
200) ![]() Mr. Smith is gazing at something as shown in the figure to the left. Suppose he does not refocus, but attempts to stare at the star shown in the figures below. Which diagram depicts how the rays from the star would travel if he does not refocus?
Mr. Smith is gazing at something as shown in the figure to the left. Suppose he does not refocus, but attempts to stare at the star shown in the figures below. Which diagram depicts how the rays from the star would travel if he does not refocus?
201) Your solitaire deck uses ♥ ♠ ♣ and your answer cards are 4 and 5. You select 4♠, 4♣, and 5♥. If the questions were Q♠ and Q♣, you would__
- a) lose 3 points
- b) lose 1 point
- c) win 1 point
- d) win 3 points
- e) be disqualified for cheating
202) Your solitaire deck uses ♥ ♠ ♣ and your answer cards are 4 and 5. You select 4♠, 5♣, and 5♥. If the questions were Q♠ and Q♣, you would__
- a) lose 3 points
- b) lose 1 point
- c) win 1 point
- d) win 3 points
- e) be disqualified for cheating
203) You solitaire deck uses ♥ ♠ ♣ and your answer cards are 4 and 5. You select 4♠, 5♣, and 5♥. If the questions were Q♠ and Q♣. Which of the following wins?
- a) K♥ and K♠
- b) K♠ and K♣
- c) K♥ and K♣
- d) two of these are true
- e) none of these are true
204) You solitaire deck uses ♥ ♠ ♣ and your answer cards are 4 and 5. You select 4♠, 5♣, and 5♥. If the questions were Q♠ and Q♣. Which of the following loses?
- a) K♥ and K♠
- b) K♠ and K♣
- c) K♥ and K♣
- d) two of these are true
- e) none of these are true
205) If you play the solitaire game 6 times, you will on average win ___ times.
- a) 4
- b) 2
- c) 3
- d) 6
- e) 5
206) If you play the solitaire game 3 times, you will on average lose ___ times.
- a) 1
- b) 2
- c) 3
- d) 4
- e) 5
207) If you play the solitaire game 6 times, you will on average lose ___ times.
- a) 4
- b) 2
- c) 3
- d) 6
- e) 5
208) If you play the solitaire game 3 times, you will on average win ___ times.
- a) 1
- b) 2
- c) 3
- d) 4
- e) 5
209) The light is linearly polarized, the electric field is oriented ________to the direction of motion
- a) parallel
- b) perpendicular
- c) at 45 degrees
- d) all of these are possible
210) Hold a pendulum a moderate distance from equilibrium and release it by tossing it in a direction perpendicular to the displacement of the mass from equilibrium. The resulting polarization will be ____ (pick the best answer)
- a) linearly
- b) circular
- c) circular or linear
- d) circular or elliptical
- e) linear or elliptical
211) A mathematically pure (strictly monochromatic) __________ wave (oscillation) that is unpolarized cannot be created
- a) electromagnetic
- b) pendulum
- c) electromagnetic or pendulum
- d) both can be created
212) To create an unpolarized pendulum oscillation
- a) create an elliptically polarized wave with an ε>0.2
- b) create an elliptically polarized wave with an ε<0.8
- c) create an elliptically polarized wave with an 0.2<ε<0.8
- d) start with a linear, circular, or elliptical wave and slowly evolve to different polarizations
213) If the hypotenuse of a 45°-45° right triangle has a length of what is the length of each side?
- a)
- b)
- c)
- d)
- e)
214) If the hypotenuse of a 45°-45° right triangle has a length of what is the length of each side?
- a)
- b)
- c)
- d)
- e)
215) If the hypotenuse of a 60°-30° right triangle has a length of 1 what is the length of the shorter side?
- a)
- b)
- c)
- d)
- e)
216) If the hypotenuse of a 60°-30° right triangle has a length of 1 what is the length of the longer side?
- a)
- b)
- c)
- d)
- e)
217) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field. By what factor does a filter reduce the electric field if it is oriented 30° to that field?
- a)
- b)
- c)
- d)
- e)
218) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field. By what factor does a filter reduce the electric field if it is oriented 60° to that field?
- a)
- b)
- c)
- d)
- e)
219) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field. A 12 mW laser strikes a polarizing filter oriented 30° to the incoming axis of polarization. How much power passes the filter?
- a) 3mW
- b) 4mW
- c) 6mW
- d) 8mW
- e) 9mW
220) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field.A 12 mW laser strikes a polarizing filter oriented 30° to the incoming axis of polarization. How much power is blocked by the filter?
- a) 3mW
- b) 4mW
- c) 6mW
- d) 8mW
- e) 9mW
221) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field.A 12 mW laser strikes a polarizing filter oriented 60° to the incoming axis of polarization. How much power is blocked by the filter?
- a) 3mW
- b) 4mW
- c) 6mW
- d) 8mW
- e) 9mW
222) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field.A 12 mW laser strikes a polarizing filter oriented 60° to the incoming axis of polarization. How much power is passed by the filter?
- a) 3mW
- b) 4mW
- c) 6mW
- d) 8mW
- e) 9mW
223) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field.A 12 mW laser strikes a polarizing filter oriented 45° to the incoming axis of polarization. How much power is passed by the filter?
- a) 3mW
- b) 4mW
- c) 6mW
- d) 8mW
- e) 9mW

- a) 1/32
- b) 1/16
- c) 3/32
- d) 1/8
- e) 3/16
225) Hold a pendulum a moderate distance from equilibrium and release it by tossing it in a direction parallel to the displacement of the mass from equilibrium. The resulting polarization will be ____ (pick the best answer)
- a) linearly
- b) circular
- c) circular or linear
- d) circular or elliptical
- e) linear or elliptical
226) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field. Unpolarized light impinges on three linear filters. The second is oriented 30° from the first, and the third is rotated by an additional 60°, making it at right angles from the first filter. What fraction of the power incident on the first filter emerges from the last?
- a) 1/32
- b) 1/16
- c) 3/32
- d) 1/8
- e) 3/16
227) If the wavelength λ associated with a photon is cut in half, the photon's energy E
- a) is cut in half
- b) is reduced by a factor of 4
- c) stays the same
- d) becomes twice as big
- e) becomes 4 times as big
228) If the wavelength λ associated with a photon doubles, the photon's frequency f
- a) is cut in half
- b) is reduced by a factor of 4
- c) stays the same
- d) becomes twice as big
- e) becomes 4 times as big
229) If the frequency f associated with a photon increases by a factor of 4, the photon's wavelength λ
- a) is cut in half
- b) is reduced by a factor of 4
- c) stays the same
- d) becomes twice as big
- e) becomes 4 times as big
230) If the frequency f associated with a photon increases by a factor of 4, the photon's energy E
- a) is cut in half
- b) is reduced by a factor of 4
- c) stays the same
- d) becomes twice as big
- e) becomes 4 times as big
231) If an atom emits two photons in a cascade emission and both photons have 2 eV of energy, the atom's energy
- a) stays the same
- b) increases by 2 eV
- c) increases by 4 eV
- d) decreases by 2 eV
- e) decreases by 4 eV
232) If an atom absorbs a photon with 2 eV energy, the atom's energy
- a) stays the same
- b) increases by 2 eV
- c) increases by 4 eV
- d) decreases by 2 eV
- e) decreases by 4 eV
233) If a 3 eV photon strikes a metal plate and causes an electron to escape, that electron will have a kinetic energy that is
- a) zero
- b) less than 3 eV
- c) equal to 3 eV
- d) greater than 3 eV
- e) equal to 6 eV
234) In the Phet lab for photoelectric effect, how was the electron's kinetic energy measured?
- a) measuring spin
- b) measuring polarization
- c) measuring both spin and polarization
- d) deflecting the electron with a magnetic field
- e) stopping the electron with an applied voltage
235) If an atom absorbs a photon with 4 eV energy, the atom's energy
- a) stays the same
- b) increases by 2 eV
- c) increases by 4 eV
- d) decreases by 2 eV
- e) decreases by 4 eV
236) If 1018 photons pass through a small hole in your roof every second, how many photons would pass through it if you doubled the diameter?
- a) 1018
- b) 2x1018
- c) 4x1018
- d) 6x1018
- e) 8x1018
237) Two black bodies of are created by cutting identical small holes in two large containers. The holes are oriented so that all the photons leaving one will enter the other. The objects have different temperature and different volume. Which object has the greater electromagnetic ("photon") energy density (energy per unit volume)?
- a) The hotter object has a greater energy density.
- b) The larger object has a greater energy density.
- c) They have the same energy density (since the holes are identical).
- d) No unique answer exists because two variables are involved (temperature and volume).
238) Two black bodies of are created by cutting identical small holes two large containers. The holes are oriented so that all the photons leaving one will enter the other. The objects have different temperature and different volume. Which object emits more photons per second (above a given threshold energy)?
- a) The object with the greater temperature emits more.
- b) The object with the greater volume.
- c) They both emit the same number of photons (since the holes are identical).
- d) No unique answer exists because two variables are involved (temperature and volume).
239) Two black bodies of are created by cutting identical small holes in two large containers. The holes are oriented so that all the photons leaving one will enter the other. The objects have different temperature and different volume. Which object has the greater electromagnetic ("photon") energy?
- a) The hotter object has a greater energy.
- b) The larger object has a greater energy.
- c) They have the same energy (since the holes are identical).
- d) No unique answer exists because two variables are involved (temperature and volume).

- a) Photons striking metal and ejecting electrons (photo-electric effect explained in 1905)
- b) Diffraction observed in light so faint that photons seemed to have no mechanism to interact with each other (observed in 1909)
- c) A system similar to the one that led to the 1901 proposal that light energy is quantized as integral multiples of hf (except that Plank assumed that the walls were conductive.)
- d) Evidence presented in 1800 that light is a wave.
- e) The transfer of energy and momentum of a high energy photon of a nearly free electron.

- a) Photons striking metal and ejecting electrons (photo-electric effect explained in 1905)
- b) Diffraction observed in light so faint that photons seemed to have no mechanism to interact with each other (observed in 1909)
- c) A system similar to the one that led to the 1901 proposal that light energy is quantized as integral multiples of hf (except that Plank assumed that the walls were conductive.)
- d) Evidence presented in 1800 that light is a wave.
- e) The transfer of energy and momentum of a high energy photon of a nearly free electron.

- a) Photons striking metal and ejecting electrons (photo-electric effect explained in 1905)
- b) Diffraction observed in light so faint that photons seemed to have no mechanism to interact with each other (observed in 1909)
- c) A system similar to the one that led to the 1901 proposal that light energy is quantized as integral multiples of hf (except that Plank assumed that the walls were conductive.)
- d) Evidence presented in 1800 that light is a wave.
- e) The transfer of energy and momentum of a high energy photon of a nearly free electron.

- a) Photons striking metal and ejecting electrons (photo-electric effect explained in 1905)
- b) Diffraction observed in light so faint that photons seemed to have no mechanism to interact with each other (observed in 1909)
- c) A system similar to the one that led to the 1901 proposal that light energy is quantized as integral multiples of hf
- d) Evidence presented in 1800 that light is a wave.
- e) The transfer of energy and momentum of a high energy photon of a nearly free electron.
244) A photon is polarized at 5° when it encounters a filter oriented at 35°. What is the probability that it passes?
- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
245) A photon is polarized at 10° when it encounters a filter oriented at 55°. What is the probability that it passes?
- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
246) A photon is polarized at 10° when it encounters a filter oriented at 70°. What is the probability that it passes?
- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
247) A photon is polarized at 10° when it encounters a filter oriented at 40°. What is the probability that it is blocked?
- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
248) A photon is polarized at 5° when it encounters a filter oriented at 50°. What is the probability that it is blocked?
- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
249) A photon is polarized at 5° when it encounters a filter oriented at 65°. What is the probability that it is blocked?
- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
250) A photon is polarized at 10° when it encounters a filter oriented at 100°. What is the probability that it passes?
- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
251) A photon is polarized at 10° when it encounters a filter oriented at 100°. What is the probability that it is blocked?
- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
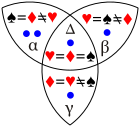
P(♠,♦) = ?
Assume the dots represent five observations.
- a) 2/4=1/2
- b) 2/5
- c) 3/5
- d) 3/4
- e) 5/6

P(♠,♥) = ?
Assume the dots represent five observations.
- a) 2/4=1/2
- b) 2/5
- c) 3/5
- d) 3/4
- e) 5/6

P(♠,♦)+P(♠,♥)+P(♥,♦) = ?
Assume the dots represent five observations.
- a) 4/5
- b) 5/6
- c) 5/4
- d) 6/5
- e) 7/5
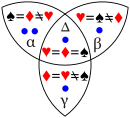
C(♠,♦) = ?
Assume the dots represent five observations.
- a) −2/5
- b) −1/5
- c) 0
- d) +1/5
- e) +2/5
- f) +1

C(♠,♥) = ?
Assume the dots represent five observations.
- a) −2/5
- b) −1/5
- c) 0
- d) +1/5
- e) +2/5
- f) +1

- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
- f) 5/4

- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
- f) 5/4

- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
- f) 5/4

- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
- f) 5/4

- a) 0
- b) 1/4
- c) 1/2
- d) 3/4
- e) 1
- f) 5/4
Answer Key
[edit | edit source]

- + 5.768E-14 N
- - 6.344E-14 N
- - 6.979E-14 N
- - 7.677E-14 N
- - 8.444E-14 N

- - 5.217E+01 degrees
- - 5.739E+01 degrees
- - 6.313E+01 degrees
- + 6.944E+01 degrees
- - 7.639E+01 degrees

is an integral that calculates the z-component of the electric field at point P situated above the x-axis where a charged rod of length (a+b) is located. The distance between point P and the x-axis is z=1.8 m. Evaluate at x=0.83 m if a=1.1 m, b=1.9 m. The total charge on the rod is 2 nC.
- - 1.040E+00 V/m2
- - 1.145E+00 V/m2
- - 1.259E+00 V/m2
- + 1.385E+00 V/m2
- - 1.523E+00 V/m2

- + 4.608E+09 N/C2
- - 5.069E+09 N/C2
- - 5.576E+09 N/C2
- - 6.134E+09 N/C2
- - 6.747E+09 N/C2
5)
is an integral that calculates the magnitude of the electric field at a distance fromthe center of a thin circular disk as measured along a line normal to the plane of the disk. The disk's radius is and the surface charge density is . Evaluate at .
- - 2.021E+00 V/m2
- - 2.224E+00 V/m2
- - 2.446E+00 V/m2
- + 2.691E+00 V/m2
- - 2.960E+00 V/m2
6) A large thin isolated square plate has an area of 9 m2. It is uniformly charged with 8 nC of charge. What is the magnitude of the electric field 3 mm from the center of the plate's surface?
- + 5.020E+01 N/C
- - 5.522E+01 N/C
- - 6.074E+01 N/C
- - 6.681E+01 N/C
- - 7.349E+01 N/C
7) What is the magnitude of the electric field at the origin if a 2.9 nC charge is placed at x = 5.9 m, and a 2.7 nC charge is placed at y = 9.2 m?
- + 8.02 x 10-1N/C
- - 9.26 x 10-1N/C
- - 1.07 x 100N/C
- - 1.23 x 100N/C
- - 1.43 x 100N/C
8) What angle does the electric field at the origin make with the x-axis if a 1.3 nC charge is placed at x = -9 m, and a 1.5 nC charge is placed at y = -5.2 m?
- - 4.15 x 101degrees
- - 4.8 x 101degrees
- - 5.54 x 101degrees
- - 6.4 x 101degrees
- + 7.39 x 101degrees
9) A dipole at the origin consists of charge Q placed at x = 0.5a, and charge of -Q placed at x = -0.5a. The absolute value of the x component of the electric field at (x,y) =( 4a, 3a) is βkQ/a2, where β equals
- - 4.1 x 10-3
- - 4.96 x 10-3
- - 6.01 x 10-3
- + 7.28 x 10-3
- - 8.82 x 10-3
10) A dipole at the origin consists of charge Q placed at x = 0.5a, and charge of -Q placed at x = -0.5a. The absolute value of the y component of the electric field at (x,y) =( 1.1a, 1.2a) is βkQ/a2, where β equals
- - 1.61 x 10-1
- - 1.95 x 10-1
- - 2.36 x 10-1
- - 2.86 x 10-1
- + 3.47 x 10-1
11) A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)?
(assuming ) , where
- - −7
- - −3
- - −3
- - 3
- + 2
12) A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the y component of the electric field at the point (5, 1)?
(assuming ) , where :
- - 5
- - s−4
- - 5−s
- + 1−s
- - s−1
13) A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the y component of the electric field at the point (5, 1)?
(assuming ) , where :
- - 1/2
- - 2/3
- - 2
- + 3/2
- - 3
14) A line of charge density λ situated on the x axis extends from x = 3 to x = 7. What is the x component of the electric field at the point (7, 8)?
(assuming ) , where :
- - s−3
- - 3−s
- - 8
- - s−7
- + 7−s
15) A line of charge density λ situated on the x axis extends from x = 3 to x = 7. What is the x component of the electric field at the point (7, 8)?
(assuming ) , where :
- - 72 + (8−s)2
- - 72 + 82
- + (7-s)2 + 82
- - 72 + (3−s)2
- - 32 + 82
16) A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)?
(assuming ) , where
- - 3−s
- - 3
- - s−7
- + 7−s
- - s−3
17) A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)?
(assuming ) , where
- - 2
- - 3
- + 3/2
- - 1/2
18) A line of charge density λ situated on the y axis extends from y = 2 to y = 7. What is the y component of the electric field at the point (2, 9)?
(assuming ) , where :
- - 2
- - s − 2
- - 2 − s
- - s − 9
- + 9 − s
19) A line of charge density λ situated on the y axis extends from y = 2 to y = 7. What is the y component of the electric field at the point (2, 9)?
(assuming ) , where :
- - 92 + (7-s)2
- - 92 + (2-s)2
- - 72 + (2-s)2
- - 22 + (7-s)2
- + 22 + (9-s)2
20) A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the y component of the electric field at the point (8, 4)?
(assuming ) , where :
- - 1/2
- + 4
- - 2
- - 8
21) A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the y component of the electric field at the point (8, 4)?
(assuming ) , where :
- - s−8
- - 8−s
- - s−4
- - 4−s
- + 4
22) A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the x component of the electric field at the point (8, 4)?
(assuming ) , where :
- - s−8
- + 8−s
- - s−4
- - 4−s
- - 4
23) A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the x component of the electric field at the point (5, 1)?
(assuming ) , where :
- + 5
- - s−4
- - 5−s
- - 1−s
- - s−1

- - 6.445E+01 N·m2/C
- - 7.089E+01 N·m2/C
- - 7.798E+01 N·m2/C
- + 8.578E+01 N·m2/C
- - 9.436E+01 N·m2/C

- - 2.058E+01 N·m2/C
- - 2.264E+01 N·m2/C
- + 2.491E+01 N·m2/C
- - 2.740E+01 N·m2/C
- - 3.014E+01 N·m2/C

- + 2.662E+01 N·m2/C
- - 2.929E+01 N·m2/C
- - 3.222E+01 N·m2/C
- - 3.544E+01 N·m2/C
- - 3.898E+01 N·m2/C
27) What is the magnetude (absolute value) of the electric flux through a rectangle that occupies the z=0 plane with corners at (x,y)= (x=0, y=0), (x=4, y=0), (x=0, y=6), and (x=4, y=6), where x and y are measured in meters. The electric field is,
- - 3.658E+02 V·m
- - 4.024E+02 V·m
- - 4.426E+02 V·m
- + 4.869E+02 V·m
- - 5.355E+02 V·m
28) Five concentric spherical shells have radius of exactly (1m, 2m, 3m, 4m, 5m).Each is uniformly charged with 2.8 nano-Coulombs. What is the magnitude of the electric field at a distance of 3.5 m from the center of the shells?
- + 6.171E+00 N/C
- - 6.789E+00 N/C
- - 7.467E+00 N/C
- - 8.214E+00 N/C
- - 9.036E+00 N/C
29) A non-conducting sphere of radius R=1.7 m has a non-uniform charge density that varies with the distnce from its center as given by ρ(r)=ar1.6 (r≤R) where a=3 nC·m-1.4. What is the magnitude of the electric field at a distance of 1.4 m from the center?
- - 1.327E+02 N/C
- - 1.460E+02 N/C
- - 1.606E+02 N/C
- + 1.767E+02 N/C
- - 1.943E+02 N/C
30) A cylinder of radius, r=3, and height, h=4, is centered at the origin and oriented along the z axis. A vector field can be expressed in cylindrical coordinates as,
Let be the outward unit normal to this cylinder and evaluate ,
over the top surface of the cylinder.
- - 6.908E+02
- + 8.369E+02
- - 1.014E+03
- - 1.228E+03
- - 1.488E+03
31) A cylinder of radius, r=3, and height, h=4, is centered at the origin and oriented along the z axis. A vector field can be expressed in cylindrical coordinates as,
Let be the outward unit normal to this cylinder and evaluate ,
over the curved side surface of the cylinder.
- - 6.457E+02
- - 7.823E+02
- - 9.477E+02
- - 1.148E+03
- + 1.391E+03
32) A cylinder of radius, r=3, and height, h=4, is centered at the origin and oriented along the z axis. A vector field can be expressed in cylindrical coordinates as,
Let be the outward unit normal to this cylinder and evaluate ,
over the entire surface of the cylinder.
- - 6.46E+02
- - 7.82E+02
- - 9.48E+02
- - 1.15E+03
- + 1.39E+03
33) A cylinder of radius, R, and height H has a uniform charge density of . The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z > H/2?
- -
- -
- -
- - none of these are correct
- +
34) A cylinder of radius, R, and height H has a uniform charge density of . The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z < H/2?
- -
- - none of these are correct
- +
- -
- -
35) A sphere has a uniform charge density of , and a radius or R. What formula describes the electric field at a distance r > R?
- - none of these are correct
- -
- -
- -
- +
36) A sphere has a uniform charge density of , and a radius equal to R. What formula describes the electric field at a distance r < R?
- -
- -
- - none of these are correct
- +
- -
37) A cylinder of radius, R, and height H has a uniform charge density of . The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r < R?
- -
- -
- +
- - none of these are correct
- -
38) A cylinder of radius, R, and height H has a uniform charge density of . The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r > R?
- -
- -
- +
- - none of these are correct
- -
39) A 5 C charge is separated from a 9 C charge by distance of 15 cm. What is the work done by increasing this separation to 21 cm?
- - 7.003E-07 J
- + 7.704E-07 J
- - 8.474E-07 J
- - 9.321E-07 J
- - 1.025E-06 J

- - 2.573E+01 J
- + 2.831E+01 J
- - 3.114E+01 J
- - 3.425E+01 J
- - 3.768E+01 J
41) A 12.0 V battery can move 9,000 C of charge. How many Joules does it deliver?
- - 8.114E+04 J
- - 8.926E+04 J
- - 9.818E+04 J
- + 1.080E+05 J
- - 1.188E+05 J
42) When a 7.85 V battery operates a 1.82 W bulb, how many electrons pass through it each second?
- - 1.087E+18 electrons
- - 1.196E+18 electrons
- - 1.316E+18 electrons
- + 1.447E+18 electrons
- - 1.592E+18 electrons
43) Calculate the final speed of a free electron accelerated from rest through a potential difference of 3 V.
- - 9.339E+05 m/s
- + 1.027E+06 m/s
- - 1.130E+06 m/s
- - 1.243E+06 m/s
- - 1.367E+06 m/s

- - 9.885E-01 N
- - 1.087E+00 N
- + 1.196E+00 N
- - 1.316E+00 N
- - 1.447E+00 N
45) Assume that a 21 nC charge is situated at the origin. Calculate the the magnitude (absolute value) of the potential difference between points P1 and P2 where the polar coordinates (r,φ) of P1 are (5 cm, 0°) and P2 is at (16 cm, 51°).
- - 2.145E+03 V
- - 2.359E+03 V
- + 2.595E+03 V
- - 2.855E+03 V
- - 3.140E+03 V

- - 9.627E+00 μC
- + 1.059E+01 μC
- - 1.165E+01 μC
- - 1.281E+01 μC
- - 1.409E+01 μC

- - 6.901E+02 V
- - 7.591E+02 V
- + 8.350E+02 V
- - 9.185E+02 V
- - 1.010E+03 V
48) If a 22 nC charge is situated at the origin, the equipotential surface for V(x,y,z)=16 V is x2 + y2 + z2 = R2, where R=
- - 8.441E+00 m
- - 9.285E+00 m
- - 1.021E+01 m
- - 1.123E+01 m
- + 1.236E+01 m
49) Two large parallel conducting plates are separated by 7.57 mm. Equal and opposite surface charges of 7.830E-07 C/m2 exist on the surfaces between the plates. What is the distance between equipotential planes which differ by 57 V?
- + 6.446E-01 mm
- - 7.412E-01 mm
- - 8.524E-01 mm
- - 9.803E-01 mm
- - 1.127E+00 mm
50) An empty parallel-plate capacitor with metal plates has an area of 1.89 m2, separated by 1.36 mm. How much charge does it store if the voltage is 4.040E+03 V?
- - 3.395E+01 μC
- - 3.735E+01 μC
- - 4.108E+01 μC
- - 4.519E+01 μC
- + 4.971E+01 μC

- - 3.515E+00 μF
- - 3.867E+00 μF
- - 4.254E+00 μF
- - 4.679E+00 μF
- + 5.147E+00 μF

- - 2.707E+01 μC
- + 2.978E+01 μC
- - 3.275E+01 μC
- - 3.603E+01 μC
- - 3.963E+01 μC

- - 8.800E+00 μJ
- - 9.680E+00 μJ
- + 1.065E+01 μJ
- - 1.171E+01 μJ
- - 1.288E+01 μJ
54) A parallel plate capacitor has both plates with an area of 1.25 m2. The separation between the plates is 0.83mm. Applied to the plates is a potential difference of 4.65 kV. What is the capacitance?
- - 8.77 nF.
- - 10.08 nF.
- - 11.6 nF.
- + 13.33 nF.
- - 15.33 nF.
55) The same parallel plate capacitor, with area 1.25 m2, plate separation 0.83mm, and an applied voltage of 4.65 kV. How much charge is stored?
- - 35.45 μC.
- - 40.77 μC.
- - 46.89 μC.
- - 53.92 μC.
- + 62.01 μC.
56) A 0.6 Farad capacitor is charged with 1.5 Coulombs. What is the value of the electric field if the plates are 0.8 mm apart?
- + 3.13 kV/m.
- - 3.59 kV/m.
- - 4.13 kV/m.
- - 4.75 kV/m.
- - 5.47 kV/m.
57) A 0.6 Farad capacitor charged with 1.5 Coulombs. What is the energy stored in the capacitor if the plates are 0.8 mm apart?
- - 1.07 J.
- - 1.23 J.
- - 1.42 J.
- - 1.63 J.
- + 1.88 J.
58) A 0.6 Farad capacitor charged with 1.5 Coulombs. What is the force between the plates if they are 0.8 mm apart?
- - 1772 N.
- - 2038 N.
- + 2344 N.
- - 2695 N.
- - 3100 N.
59) How fast is a 2212 eV electron moving?
- - 8.3 x 106 m/s.
- - 1.2 x 107 m/s.
- - 1.9 x 107 m/s.
- + 2.8 x 107 m/s.
- - 4.2 x 107 m/s.
60) A proton is accelerated (at rest) from a plate held at 552.1 volts to a plate at zero volts. What is the final speed?
- + 3.3 x 105 m/s.
- - 4.9 x 105 m/s.
- - 7.3 x 105 m/s.
- - 1.1 x 106 m/s.
- - 1.6 x 106 m/s.
61) What voltage is required accelerate an electron at rest to a speed of 9.7 x 104 m/s?
- - 1.8 x 10-2 volts
- + 2.7 x 10-2 volts
- - 4 x 10-2 volts
- - 6 x 10-2 volts
- - 9 x 10-2 volts
62) What voltage is required to stop a proton moving at a speed of 3 x 104 m/s?
- - 1.4 x 100 volts
- - 2.1 x 100 volts
- - 3.1 x 100 volts
- + 4.7 x 100 volts
- - 7 x 100 volts
63) What is the average current involved when a truck battery sets in motion 702 C of charge in 2.92 s while starting an engine?
- + 2.404E+02 A
- - 2.645E+02 A
- - 2.909E+02 A
- - 3.200E+02 A
- - 3.520E+02 A
64) The charge passing a plane intersecting a wire is , where =38 C and 0.0106 s. What is the current at 0.0123 s?
- - 1.021E+03 A
- + 1.123E+03 A
- - 1.236E+03 A
- - 1.359E+03 A
- - 1.495E+03 A
65) Calculate the drift speed of electrons in a copper wire with a diameter of 3.32 mm carrying a 18.4 A current, given that there is one free electron per copper atom. The density of copper is 8.80 x 103kg/m3 and the atomic mass of copper is 63.54 g/mol. Avagadro's number is 6.02 x 1023atoms/mol.
- - 1.195E-04 m/s
- - 1.315E-04 m/s
- - 1.446E-04 m/s
- + 1.591E-04 m/s
- - 1.750E-04 m/s
66) A make-believe metal has a density of 5.880E+03 kg/m3 and an atomic mass of 73.2 g/mol. Taking Avogadro's number to be 6.020E+23 atoms/mol and assuming one free electron per atom, calculate the number of free electrons per cubic meter.
- - 4.396E+28 e−/m3
- + 4.836E+28 e−/m3
- - 5.319E+28 e−/m3
- - 5.851E+28 e−/m3
- - 6.436E+28 e−/m3
67) A device requires consumes 121 W of power and requires 5.12 A of current which is supplied by a single core 10-guage (2.588 mm diameter) wire. Find the magnitude of the average current density.
- - 8.849E+05 A/m2
- + 9.734E+05 A/m2
- - 1.071E+06 A/m2
- - 1.178E+06 A/m2
- - 1.296E+06 A/m2
68) Calculate the resistance of a 12-gauge copper wire that is 97 m long and carries a current of 29 mA. The resistivity of copper is 1.680E-08 Ω·m and 12-gauge wire as a cross-sectional area of 3.31 mm2.
- + 4.923E-01 Ω
- - 5.416E-01 Ω
- - 5.957E-01 Ω
- - 6.553E-01 Ω
- - 7.208E-01 Ω
69) Calculate the electric field in a 12-gauge copper wire that is 75 m long and carries a current of 21 mA. The resistivity of copper is 1.680E-08 Ω·m and 12-gauge wire as a cross-sectional area of 3.31 mm2.
- - 7.280E-05 V/m
- - 8.008E-05 V/m
- - 8.809E-05 V/m
- - 9.690E-05 V/m
- + 1.066E-04 V/m
70) Imagine a substance could be made into a very hot filament. Suppose the resitance is 2.14 Ω at a temperature of 77°C and that the temperature coefficient of expansion is 4.750E-03 (°C)−1). What is the resistance at a temperature of 542 °C?
- - 6.540E+00 Ω
- + 6.867E+00 Ω
- - 7.210E+00 Ω
- - 7.571E+00 Ω
- - 7.949E+00 Ω
71) A DC winch moter draws 31 amps at 191 volts as it lifts a 5.080E+03 N weight at a constant speed of 0.99 m/s. Assuming that all the electrical power is either converted into gravitational potential energy or ohmically heats the motor's coils, calculate the coil's resistance.
- - 6.972E-01 Ω
- - 7.669E-01 Ω
- - 8.436E-01 Ω
- + 9.280E-01 Ω
- - 1.021E+00 Ω
72) What is consumer cost to operate one 77−W incandescent bulb for 12 hours per day for 1 year (365 days) if the cost of electricity is $0.134 per kilowatt-hour?
- - $3.087E+01
- - $3.395E+01
- - $3.735E+01
- - $4.108E+01
- + $4.519E+01
73) A given battery has a 12 V emf and an internal resistance of 0.193 Ω. If it is connected to a 0.89 Ω resistor what is the power dissipated by that load?
- - 8.210E+01 W
- - 9.030E+01 W
- - 9.934E+01 W
- + 1.093E+02 W
- - 1.202E+02 W
74) A battery with a terminal voltage of 14.9 V is connected to a circuit consisting of 2 23.3 Ω resistors and one 13.6 Ω resistor. What is the voltage drop across the 13.6 Ω resistor?
- + 3.366E+00 V
- - 3.703E+00 V
- - 4.073E+00 V
- - 4.480E+00 V
- - 4.928E+00 V
75) Three resistors, R1 = 1.7 Ω, and R2 = R2 = 3.75 Ω, are connected in parallel to a 9.74 V voltage source. Calculate the power dissipated by the smaller resistor (R1.)
- - 4.193E+01 W
- - 4.612E+01 W
- - 5.073E+01 W
- + 5.580E+01 W
- - 6.138E+01 W

- + 2.993E+01 W
- - 3.293E+01 W
- - 3.622E+01 W
- - 3.984E+01 W
- - 4.383E+01 W

- - 8.841E-02 A
- + 9.725E-02 A
- - 1.070E-01 A
- - 1.177E-01 A
- - 1.294E-01 A

- - 1.726E+00 mA
- - 1.898E+00 mA
- - 2.088E+00 mA
- + 2.297E+00 mA
- - 2.527E+00 mA

- - 1.276E+01 V
- - 1.404E+01 V
- + 1.544E+01 V
- - 1.699E+01 V
- - 1.869E+01 V

- - 1.981E+01 V
- + 2.180E+01 V
- - 2.398E+01 V
- - 2.637E+01 V
- - 2.901E+01 V

- - 1.084E+01 s
- - 1.192E+01 s
- - 1.311E+01 s
- + 1.442E+01 s
- - 1.586E+01 s
82) A 5.3 volt battery moves 11 Coulombs of charge in 2.1 hours. What is the power?
- + 7.71 x 10-3 W
- - 9.34 x 10-3 W
- - 1.13 x 10-2 W
- - 1.37 x 10-2 W
- - 1.66 x 10-2 W
83) The diameter of a copper wire is 1.7 mm, and it carries a current of 92 amps. What is the drift velocity if copper has a density of 8.8E3 kg/m3 and an atomic mass of 63.54 g/mol? (1 mol = 6.02E23 atoms, and copper has one free electron per atom.)
- - 2.07 x 10-3m/s
- - 2.5 x 10-3m/s
- + 3.03 x 10-3m/s
- - 3.67 x 10-3m/s
- - 4.45 x 10-3m/s
84) A 164 Watt DC motor draws 0.25 amps of current. What is effective resistance?
- - 1.22 x 103 Ω
- - 1.48 x 103 Ω
- - 1.79 x 103 Ω
- - 2.17 x 103 Ω
- + 2.62 x 103 Ω
85) A power supply delivers 149 watts of power to a 153 ohm resistor. What was the applied voltage?
- - 8.49 x 101 volts
- - 1.03 x 102 volts
- - 1.25 x 102 volts
- + 1.51 x 102 volts
- - 1.83 x 102 volts
86) 3 amps flow through a 1 Ohm resistor. What is the voltage?
- +
- -
- -
- - None these are correct.
87) A 1 ohm resistor has 5 volts DC across its terminals. What is the current (I) and the power consumed?
- - I = 5A & P = 3W.
- - I = 5A & P = 5W.
- + I = 5A & P = 25W.
- - I = 5A & P = 9W
88) The voltage across two resistors in series is 10 volts. One resistor is twice as large as the other. What is the voltage across the larger resistor? What is the voltage across the smaller one?
- - and.
- - and .
- + and .
- - None of these are true.
89) A 1 ohm, 2 ohm, and 3 ohm resistor are connected in series. What is the total resistance?
- - .
- - .
- + .
- - None of these are true.
90) Two identical resistors are connected in series. The voltage across both of them is 250 volts. What is the voltage across each one?
- - and .
- - None of these are true.
- + and .
- - and .
91) A 1 ohm, 2 ohm, and 3 ohm resistor are connected in parallel. What is the total resistance?
- - .
- - .
- + .
- - .
92) A 5 ohm and a 2 ohm resistor are connected in parallel. What is the total resistance?
- - .
- - .
- - .
- + .
93) A 7 ohm and a 3 ohm resistor are connected in parallel. What is the total resistance?
- + .
- - .
- - .
- - .
94) Three 1 ohm resistors are connected in parallel. What is the total resistance?
- - .
- + .
- - .
- - .
95) If you put an infinite number of resistors in parallel, what would the total resistance be?
- + would approach Zero as The No. of Resistors In parallel Approaches Infinity.
- - None of these are true.
- - would approach 1 as The No. of Resistors In parallel Approaches Infinity
- - It is not possible to connect that Number of Resistors in parallel.
97) Why do we say the "voltage across" or "the voltage with respect to?" Why can't we just say voltage?
- - It's an Electrical Cliche.
- - The other point could be Negative or positive.
- - None these are correct
- + Voltage is a measure of Electric Potential difference between two electrical points.
- - ; ; ; ..
- - ; ; ; .
- + ; ; ; .
- - ; ; ; .
99) Two resistors are in parallel with a voltage source. How do their voltages compare?
- + The voltage across both resistors is the same as the source.
- - None of these are true.
- - One has full voltage, the other has none.
- - The voltage across both resistors is half the voltage of the source.
100) A resistor consumes 5 watts, and its current is 10 amps. What is its voltage?
- - 2V.
- - 10V.
- + 0.5V.
- - 15V.
101) A resistor has 10 volts across it and 4 amps going through it. What is its resistance?
- - None of these are true.
- -
- -
- +
102) If you plot voltage vs. current in a circuit, and you get a linear line, what is the significance of the slope?
- - Power.
- + Resistance.
- - Discriminant.
- - None of these are true.
103) A resistor has 3 volts across it. Its resistance is 1.5 ohms. What is the current?
- - 12A
- - 3A
- + 2A
- - 1.5A
104) A resistor has 8 volts across it and 3 Amps going through it. What is the power consumed?
- - 2.2W
- + 24W
- - 8W
- - 3W
105) A resistor has a voltage of 5 volts and a resistance of 15 ohms. What is the power consumed?
- - None of these are ture.
- - 11.67 Joules
- + 1.67 Watts
- - 2.5 Watts
106) A resistor is on for 5 seconds. It consumes power at a rate of 5 watts. How many joules are used?
- + 25 Joules
- - 3 Joules
- - 5 Joules
- - None of these are true
107) An ideal 6.1 V voltage source is connected to two resistors in parallel. One is 2.4, and the other is 4.2 . What is the current through the larger resistor?
- - 0.61 mA.
- - 0.7 mA.
- - 0.8 mA.
- + 0.92 mA.
- - 1.06 mA.
108) A 6 ohm resistor is connected in series to a pair of 5 ohm resistors that are in parallel. What is the net resistance?
- - 7.4 ohms.
- + 8.5 ohms.
- - 9.8 ohms.
- - 11.2 ohms.
- - 12.9 ohms.
109) Two 8.8 ohm resistors are connected in parallel. This combination is then connected in series to a 2.8 ohm resistor. What is the net resistance?
- - 6.3 ohms.
- + 7.2 ohms.
- - 8.3 ohms.
- - 9.5 ohms.
- - 11 ohms.
110) An ideal 6 volt battery is connected to a 0.073 ohm resistor. To measure the current an ammeter with a resistance of 14 is used. What current does the ammeter actually read?
- - 60 A.
- + 69 A.
- - 79.3 A.
- - 91.2 A.
- - 104.9 A.
111) A battery has an emf of 6.1 volts, and an internal resistance of 366 . It is connected to a 3.6 resistor. What power is developed in the 3.6 resistor?
- - 6.44 W.
- - 7.41 W.
- + 8.52 W.
- - 9.79 W.
- - 11.26 W.
112) An alpha-particle (q=3.2x10−19C) moves through a uniform magnetic field that is parallel to the positive z-axis with magnitude 5.11 T. What is the x-component of the force on the alpha-particle if it is moving with a velocity
(8.99 i + 7.56 j + 8.49 k) x 104 m/s?
- - 1.124E-13 N
- + 1.236E-13 N
- - 1.360E-13 N
- - 1.496E-13 N
- - 1.645E-13 N
113) A charged particle in a magnetic field of 2.780E-04 T is moving perpendicular to the magnetic field with a speed of 6.370E+05 m/s. What is the period of orbit if orbital radius is 0.671 m?
- - 6.017E-06 s
- + 6.619E-06 s
- - 7.280E-06 s
- - 8.008E-06 s
- - 8.809E-06 s
114) An alpha-particle (m=6.64x10−27kg, q=3.2x10−19C) briefly enters a uniform magnetic field of magnitude 0.0783 T . It emerges after being deflected by 64° from its original direction. How much time did it spend in that magnetic field?
- - 2.224E-07 s
- - 2.446E-07 s
- - 2.691E-07 s
- + 2.960E-07 s
- - 3.256E-07 s
115) A 18 cm-long horizontal wire is maintained in static equilibrium by a horizontally directed magnetic field that is perpendicular to the wire (and to Earth's gravity). The mass of the wire is 8 g, and the magnitude of the magnetic field is 0.351 T. What current is required to maintain this balance?
- + 1.241E+00 A
- - 1.365E+00 A
- - 1.501E+00 A
- - 1.652E+00 A
- - 1.817E+00 A
116) A long rigid wire carries a 8 A current. What is the magnetic force per unit length on the wire if a 0.899 T magnetic field is directed 43° away from the wire?
- - 3.685E+00 N/m
- - 4.054E+00 N/m
- - 4.459E+00 N/m
- + 4.905E+00 N/m
- - 5.395E+00 N/m
117) A circular current loop of radius 2.86 cm carries a current of 1.7 mA. What is the magnitude of the torque if the dipole is oriented at 43 ° to a uniform magnetic fied of 0.729 T?
- - 1.483E-06 N m
- - 1.632E-06 N m
- - 1.795E-06 N m
- - 1.974E-06 N m
- + 2.172E-06 N m
118) An electron beam (m=9.1 x 10−31kg, q=1.6 x 10−19C) enters a crossed-field velocity selector with magnetic and electric fields of 5.53 mT and 7.210E+03 N/C, respectively. What must the velocity of the electron beam be to transverse the crossed fields undeflected ?
- - 8.905E+05 m/s
- - 9.796E+05 m/s
- - 1.078E+06 m/s
- - 1.185E+06 m/s
- + 1.304E+06 m/s

- - 1.255E-06 V
- - 1.380E-06 V
- - 1.518E-06 V
- - 1.670E-06 V
- + 1.837E-06 V
120) A cyclotron used to accelerate alpha particlesm=6.64 x 10−27kg, q=3.2 x 10−19C) has a radius of 0.398 m and a magneticfield of 0.855 T. What is their maximum kinetic energy?
- + 5.581E+00 MeV
- - 6.139E+00 MeV
- - 6.753E+00 MeV
- - 7.428E+00 MeV
- - 8.171E+00 MeV
121) A wire carries a current of 316 A in a circular arc with radius 1.55 cm swept through 76 degrees. Assuming that the rest of the current is 100% shielded by mu-metal, what is the magnetic field at the center of the arc?
- - 8.070E+00 Tesla
- + 8.878E+00 Tesla
- - 9.765E+00 Tesla
- - 1.074E+01 Tesla
- - 1.182E+01 Tesla

- - Bx= 4.887E-05 T
- + Bx= 5.376E-05 T
- - Bx= 5.914E-05 T
- - Bx= 6.505E-05 T
- - Bx= 7.156E-05 T

- - By= 5.510E-05 T
- - By= 6.061E-05 T
- + By= 6.667E-05 T
- - By= 7.333E-05 T
- - By= 8.067E-05 T
124) Two parallel wires each carry a 5.0 mA current and are oriented in the z direction. The first wire is located in the x-y plane at (4.48 cm, 0.973 cm), while the other is located at (3.32 cm, 4.79 cm). What is the force per unit length between the wires?
- - 1.139E-10 N/m
- + 1.253E-10 N/m
- - 1.379E-10 N/m
- - 1.517E-10 N/m
- - 1.668E-10 N/m
125) Two loops of wire carry the same current of 62 kA, and flow in the same direction. They share a common axis and orientation. One loop has a radius of 0.584 m while the other has a radius of 1.38 m. What is the magnitude of the magnetic field at a point on the axis of both loops, situated between the loops at a distance 0.341 m from the first (smaller) loopif the disance between the loops is 1.21 m?
- - 4.102E-02 T
- - 4.513E-02 T
- - 4.964E-02 T
- - 5.460E-02 T
- + 6.006E-02 T
126) Under most conditions the current is distributed uniformly over the cross section of the wire. What is the magnetic field 1.34 mm from the center of a wire of radius 3 mm if the current is 1A?
- - 2.237E-05 T
- - 2.461E-05 T
- - 2.707E-05 T
- + 2.978E-05 T
- - 3.276E-05 T
127) The Z-pinch is an (often unstable) cylindrical plasma in which a aximuthal magnetic field is produced by a current in the z direction. A simple model for the magnetic field, valid for is,
,
where is the maximum magnetic field (at ). If 0.703 m and 0.521 T, then how much current (in the z-direction) flows through a circle of radius 0.165 m that is centered on the axis with its plane perpendicular to the axis?
- - 1.338E+05 A
- - 1.472E+05 A
- - 1.619E+05 A
- + 1.781E+05 A
- - 1.959E+05 A

:
- - 1.547E-03 T-m
- - 1.702E-03 T-m
- + 1.872E-03 T-m
- - 2.060E-03 T-m
- - 2.266E-03 T-m

:
- - 4.069E-03 T-m
- - 4.476E-03 T-m
- - 4.924E-03 T-m
- + 5.416E-03 T-m
- - 5.958E-03 T-m
130) A solenoid has 8.230E+04 turns wound around a cylinder of diameter 1.5 cm and length 18 m. The current through the coils is 0.633 A. Define the origin to be the center of the solenoid and neglect end effects as you calculate the line integral alongthe axis from z=−3.74 cm to z=+3.23 cm
- - 1.731E-04 T-m
- - 1.905E-04 T-m
- - 2.095E-04 T-m
- - 2.305E-04 T-m
- + 2.535E-04 T-m
131) A long coil is tightly wound around a (hypothetical) ferromagnetic cylinder. If n= 20 turns per centimeter and the current applied to the solenoid is 598 mA, the net magnetic field is measured to be 1.38 T. What is the magnetic susceptibility for this case?
- - 8.338E+02
- + 9.172E+02
- - 1.009E+03
- - 1.110E+03
- - 1.221E+03
132) A cosmic ray alpha particle encounters Earth's magnetic field at right angles to a field of 11.4 μT. The kinetic energy is 307 keV. What is the radius of particle's orbit?
- - 7 x 101 m.
- - 2.2 x 102 m.
- - 7 x 102 m.
- - 2.2 x 103 m.
- + 7 x 103 m.
133) Two parallel wires are 6.7 meters long, and are separated by 5.7 mm. What is the force if both wires carry a current of 13.3 amps?
- - 4.16 x 10-4 newtons
- - 1.32 x 10-3 newtons
- - 4.16 x 10-3 newtons
- - 1.32 x 10-2 newtons
- + 4.16 x 10-2 newtons
134) Blood is flowing at an average rate of 20.5 cm/s in an artery that has an inner diameter of 4.5 mm. What is the voltage across a hall probe placed across the inner diameter of the artery if the perpendicular magnetic field is 0.12 Tesla?
- - 3.5 x 10-5 Volts
- + 1.11 x 10-4 Volts
- - 3.5 x 10-4 Volts
- - 1.11 x 10-3 Volts
- - 3.5 x 10-3 Volts
135) An electron tube on Earth's surface is oriented horizontally towards magnetic north. The electron is traveling at 0.07c, and Earth's magnetic field makes an angle of 47.5 degrees with respect to the horizontal. To counter the magnetic force, a voltage is applied between two large parallel plates that are 57 mm apart. What must be the applied voltage if the magnetic field is 46μT?
- - 4.1 x 100 volts
- - 1.3 x 101 volts
- + 4.1 x 101 volts
- - 1.3 x 102 volts
- - 4.1 x 102 volts
136) Amphere's law for magnetostatic currents is that equals the current enclosed by the closed loop, and is the magnetic field. A current of 8.2A flows upward along the z axis. Noting that for this geometry, , calculate the line integral for a circle of radius 9.6m.
- + 6.03E+01 m
- - 6.61E+01 m
- - 7.25E+01 m
- - 7.95E+01 m
- - 8.72E+01 m
137) If , where is magnetic field, what is at a distance of 9.6m from a wire carrying a current of 8.2A?
- - 1.24E-01 A/m
- + 1.36E-01 A/m
- - 1.49E-01 A/m
- - 1.63E-01 A/m
- - 1.79E-01 A/m
138) If , where is magnetic field, what is at the point (8.6443,4.1757) if a current of 8.2A flows through a wire that runs along the z axis?
- - 8.47E-02 A/m
- - 9.29E-02 A/m
- - 1.02E-01 A/m
- - 1.12E-01 A/m
- + 1.22E-01 A/m
139) A very long and thin solenoid has 2705 turns and is 134 meters long. The wire carrys a current of 8.2A. What is the magnetic field in the center?
- - 1.90E-04 Tesla
- + 2.08E-04 Tesla
- - 2.28E-04 Tesla
- - 2.50E-04 Tesla
- - 2.74E-04 Tesla
140) A very long and thin solenoid has 1223 turns and is 134 meters long. The wire carrys a current of 8.2A. If this solenoid is sufficiently thin, what is the line integral of along an on-axis path that starts 28 meters from the center and stops 93 meters from the center?
- - 2.21E+03 A
- - 2.43E+03 A
- - 2.66E+03 A
- + 2.92E+03 A
- - 3.20E+03 A
141) What is the sum of 5.2 apples plus 76 apples?
- - 7.41E+01 apples
- + 8.12E+01 apples
- - 8.90E+01 apples
- - 9.76E+01 apples
- - 1.07E+02 apples
142) H is defined by, B=μ0H, where B is magnetic field. A current of 52A passes along the z-axis. Use symmetry to find the integral, , from the point (0,7.5) to the point (7.5,0).
- - 1.19E+01 amps
- + 1.30E+01 amps
- - 1.43E+01 amps
- - 1.56E+01 amps
- - 1.71E+01 amps
143) H is defined by, B=μ0H, where B is magnetic field. A current of 96A passes along the z-axis. Use symmetry to find the integral, , from the point (-6.6, 6.6) to the point (6.6, 6.6).
- - 1.82E+01 amps
- - 2.00E+01 amps
- - 2.19E+01 amps
- + 2.40E+01 amps
- - 2.63E+01 amps
144) H is defined by, B=μ0H, where B is magnetic field. A current of 33A passes along the z-axis. Use symmetry to find the integral, , from the point (0,9.5) to the point (9.5,9.5).
- - 3.43E+00 amps
- - 3.76E+00 amps
- + 4.13E+00 amps
- - 4.52E+00 amps
- - 4.96E+00 amps
145) H is defined by, B=μ0H, where B is magnetic field. A current of 94A passes along the z-axis. Use symmetry to find the integral, , from (-∞,6.2) to (+∞,6.2).
- - 3.91E+01 amps
- - 4.29E+01 amps
- + 4.70E+01 amps
- - 5.15E+01 amps
- - 5.65E+01 amps
146) A square coil has sides that are L= 0.673 m long and is tightly wound with N=211 turns of wire. The resistance of the coil is R=5.31 Ω. The coil is placed in a spacially uniform magnetic field that is directed perpendicular to the face of the coil and whose magnitude is increasing at a rate dB/dt=0.0454 T/s. If R represents the only impedance of the coil, what is the magnitude of the current circulting through it?
- - 6.753E-01 A
- - 7.428E-01 A
- + 8.171E-01 A
- - 8.988E-01 A
- - 9.887E-01 A
147) A time dependent magnetic field is directed perpendicular to the plane of a circular coil with a radius of 0.317 m. The magnetic field is spatially uniform but decays in time according to , where 6.25 s. What is the current in the coil if the impedance of the coil is 52.3 Ω?
- - 6.717E-02 A
- - 7.388E-02 A
- - 8.127E-02 A
- + 8.940E-02 A
- - 9.834E-02 A
148) The current through the windings of a solenoid with n= 2.120E+03 turns per meter is changing at a rate dI/dt=4 A/s. The solenoid is 94 cm long and has a cross-sectional diameter of 2.56 cm. A small coil consisting of N=30turns wraped in a circle of diameter 1.15 cm is placed in the middle of the solenoid such that the plane of the coil is perpendicular to the central axis of the solenoid. Assume that the infinite-solenoid approximation is valid inside the small coil. What is the emf induced in the coil?
- - 3.019E-05 V
- + 3.321E-05 V
- - 3.653E-05 V
- - 4.018E-05 V
- - 4.420E-05 V
149) Calculate the motional emf induced along a 40.1 km conductor moving at an orbital speed of 7.85 km/s perpendicular to Earth's 5.160E-05 Tesla magnetic field.
- - 1.477E+04 V
- + 1.624E+04 V
- - 1.787E+04 V
- - 1.965E+04 V
- - 2.162E+04 V

--(Answer & Why this question is different.)
- - 6.980E+00 cm3/s
- - 7.678E+00 cm3/s
- - 8.446E+00 cm3/s
- - 9.290E+00 cm3/s
- + 1.022E+01 cm3/s
151) A recangular coil with an area of 0.371 m2 and 20 turns is placed in a uniform magnetic field of 2.51 T. The coil is rotated about an axis that is perpendicular to this field. At time t=0 the normal to the coil is oriented parallel to the magnetic field and the coil is rotating with a constant angular frequency of 3.060E+03 s−1. What is the magnitude (absolute value) of the induced emf at t = 88 s?
- + 5.694E+04 V
- - 6.263E+04 V
- - 6.889E+04 V
- - 7.578E+04 V
- - 8.336E+04 V
152) A spatially uniform magnetic points in the z-direction and oscilates with time as where 3.26 T and 9.250E+03 s−1. Suppose the electric field is always zero at point , and consider a circle of radius 0.385 m that is centered at that point and oriented in a plane perpendicular to the magnetic field. Evaluate the maximum value of the line integral around the circle.
- - 6.029E+04 V
- - 6.631E+04 V
- + 7.295E+04 V
- - 8.024E+04 V
- - 8.826E+04 V
153) A long solenoid has a radius of 0.442 m and 63 turns per meter; its current decreases with time according to , where 7 A and 22 s−1.What is the induced electric fied at a distance 1.94 m from the axis at time t=0.0331 s ?
- + 2.964E-04 V/m
- - 3.260E-04 V/m
- - 3.586E-04 V/m
- - 3.945E-04 V/m
- - 4.339E-04 V/m
154) A long solenoid has a radius of 0.508 m and 90 turns per meter; its current decreases with time according to , where 7 A and 25 s−1.What is the induced electric fied at a distance 0.145 m from the axis at time t=0.0643 s ?
- - 2.614E-04 V/m
- + 2.875E-04 V/m
- - 3.163E-04 V/m
- - 3.479E-04 V/m
- - 3.827E-04 V/m

- - 6.667E-02 V
- - 7.334E-02 V
- - 8.067E-02 V
- - 8.874E-02 V
- + 9.762E-02 V
156) An induced emf of 4.82V is measured across a coil of 73 closely wound turns while the current throuth it increases uniformly from 0.0 to 4.61A in 0.934s. What is the self-inductance of the coil?
- - 7.337E-01 H
- - 8.071E-01 H
- - 8.878E-01 H
- + 9.765E-01 H
- - 1.074E+00 H
157) A washer has an inner diameter of 2.57 cm and an outer diamter of 4.14 cm. The thickness is where is measured in cm, , and . What is the volume of the washer?
- - 7.226E-01 cm3
- - 7.949E-01 cm3
- - 8.744E-01 cm3
- - 9.618E-01 cm3
- + 1.058E+00 cm3

- - 4.109E-01 V
- - 4.930E-01 V
- - 5.917E-01 V
- + 7.100E-01 V
- - 8.520E-01 V

- + -1.442E+00 s
- - -1.586E+00 s
- - -1.744E+00 s
- - -1.919E+00 s
- - -2.111E+00 s
160) In an LC circuit, the self-inductance is 0.0134 H and the capacitance is 3.280E-06 F. At t=0 all the energy is stored in the capacitor, which has a charge of 5.930E-05 C. How long does it take for the capacitor to become completely discharged?
- - 2.722E-04 s
- - 2.994E-04 s
- + 3.293E-04 s
- - 3.622E-04 s
- - 3.985E-04 s
161) An ac generator produces an emf of amplitude 78 V at a frequency of 45 Hz. What is the maximum amplitude of the current if the generator is connected to a 60 mF inductor?
- - 3.140E+00 A
- - 3.454E+00 A
- - 3.800E+00 A
- - 4.180E+00 A
- + 4.598E+00 A
162) An ac generator produces an emf of amplitude 64 V at a frequency of 95 Hz. What is the maximum amplitude of the current if the generator is connected to a 99 mF capacitor?
- - 3.126E+00 A
- - 3.438E+00 A
- + 3.782E+00 A
- - 4.160E+00 A
- - 4.576E+00 A
163) The output of an ac generator connected to an RLC series combination has a frequency of 510 Hz and an amplitude of 0.69 V;. If R =4 Ω, L= 4.30E-03H , and C=9.20E-04 F, what is the impedance?
- - 1.054E+01 Ω
- - 1.159E+01 Ω
- - 1.275E+01 Ω
- + 1.402E+01 Ω
- - 1.542E+01 Ω
164) The output of an ac generator connected to an RLC series combination has a frequency of 480 Hz and an amplitude of 0.17 V;. If R =5 Ω, L= 6.70E-03H , and C=6.30E-04 F, what is the magnitude (absolute value) of the phase difference between current and emf?
- + 1.322E+00 &rad;
- - 1.454E+00 &rad;
- - 1.600E+00 &rad;
- - 1.760E+00 &rad;
- - 1.936E+00 &rad;
165) The output of an ac generator connected to an RLC series combination has a frequency of 8.20E+04 Hz and an amplitude of 4 V. If R =5 Ω, L= 5.40E-03H , and C=9.80E-06 F, what is the rms power transferred to the resistor?
- - 1.865E-04 Watts
- + 2.051E-04 Watts
- - 2.256E-04 Watts
- - 2.482E-04 Watts
- - 2.730E-04 Watts
166) An RLC series combination is driven with an applied voltage of of V=V0sin(ωt), where V0=0.38 V. The resistance, inductance, and capacitance are R =7 Ω, L= 4.10E-03H , and C=7.40E-04 F, respectively. What is the amplitude of the current?
- - 4.486E-02 A
- - 4.935E-02 A
- + 5.429E-02 A
- - 5.971E-02 A
- - 6.569E-02 A
167) The quality factor Q is a dimensionless paramater involving the relative values of the magnitudes of the at three impedances (R, XL, XC). Since Q is calculatedat resonance, XL, XC and only twoimpedances are involved, Q=≡ω0L/R is definedso that Q is large if the resistance is low. Calculate the Q of an LRC series driven at resonance by an applied voltage of of V=V0sin(ωt), where V0=1 V. The resistance, inductance, and capacitance are R =0.21 Ω, L= 4.80E-03H , and C=3.60E-06 F, respectively.
- + Q = 1.739E+02
- - Q = 2.000E+02
- - Q = 2.300E+02
- - Q = 2.645E+02
- - Q = 3.041E+02
168) A step-down transformer steps 19 kV down to 220 V. The high-voltage input is provided by a 250 Ω power line that carries 4 A of currentWhat is the output current (at the 220 V side ?)
- - 2.595E+02 A
- - 2.855E+02 A
- - 3.140E+02 A
- + 3.455E+02 A
- - 3.800E+02 A
169) Two orbiting satellites are orbiting at a speed of 77 km/s perpendicular to a magnetic field of 56 μT. They are connected by a cable that is 31 km long. A voltmeter is attached between a satellite and one end of the cable. The voltmeter's internal impedance far exceeds the net resistance through the ionosphere that completes the circuit. What is the measured voltage?
- - 1.1 x 105 volts.
- + 1.34 x 105 volts.
- - 1.62 x 105 volts.
- - 1.96 x 105 volts.
- - 2.38 x 105 volts.
170) An loop of wire with 26 turns has a radius of 0.26 meters, and is oriented with its axis parallel to a magetic field of 0.75 Tesla. What is the induced voltage if this field is reduced to 13% of its original value in 1.8 seconds?
- + 2 x 100 volts
- - 2.42 x 100 volts
- - 2.94 x 100 volts
- - 3.56 x 100 volts
- - 4.31 x 100 volts
171) A 547 mF capacitor is connected in series to a 2 kΩ resistor. If the capacitor is discharged, how long does it take to fall by a factor of e4? (where e =2.7...)
- - 1.38 x 103 s.
- + 4.38 x 103 s.
- - 1.38 x 104 s.
- - 4.38 x 104 s.
- - 1.38 x 105 s.
172) A 665 μF capacitor is connected in series to a 806 kΩ resistor. If the capacitor is discharged, how long does it take to fall by a factor of e2? (where e =2.7...)
- - 3.39 x 101 s.
- - 1.07 x 102 s.
- - 3.39 x 102 s.
- + 1.07 x 103 s.
- - 3.39 x 103 s.
173) A 206 mF capacitor is connected in series to a 990 MΩ resistor. If the capacitor is discharged, how long does it take to fall by a factor of e4? (where e =2.7...)
- + 8.16 x 108 s.
- - 2.58 x 109 s.
- - 8.16 x 109 s.
- - 2.58 x 1010 s.
- - 8.16 x 1010 s.
174) A 5 F capacitor is connected in series to a 8Ω resistor. If the capacitor is discharged, how long does it take to fall by a factor of e4? (where e =2.7...)
- - 1.6 x 101 s.
- - 5.06 x 101 s.
- + 1.6 x 102 s.
- - 5.06 x 102 s.
- - 1.6 x 103 s.

- - 3.876E+01 V
- - 4.263E+01 V
- - 4.690E+01 V
- + 5.159E+01 V
- - 5.674E+01 V

- - 3.765E+03 V/m
- - 4.142E+03 V/m
- - 4.556E+03 V/m
- - 5.012E+03 V/m
- + 5.513E+03 V/m

- - 7.089E-02 A
- - 7.798E-02 A
- - 8.578E-02 A
- + 9.436E-02 A
- - 1.038E-01 A
178) A 46 kW radio transmitter on Earth sends it signal to a satellite 140 km away. At what distance in the same direction would the signal have the same maximum field strength if the transmitter's output power were increased to 73 kW?
- + 1.764E+02 km
- - 1.940E+02 km
- - 2.134E+02 km
- - 2.347E+02 km
- - 2.582E+02 km
179) What is the radiation pressure on an object that is 5.90E+11 m away from the sun and has cross-sectional area of 0.014 m2? The average power output of the Sun is 3.80E+26 W.
- - 5.268E-07 N/m2
- + 5.795E-07 N/m2
- - 6.375E-07 N/m2
- - 7.012E-07 N/m2
- - 7.713E-07 N/m2
180) What is the radiation force on an object that is 5.20E+11 m away from the sun and has cross-sectional area of 0.04 m2? The average power output of the Sun is 3.80E+26 W.
- - 2.242E-08 N
- - 2.466E-08 N
- - 2.713E-08 N
- + 2.984E-08 N
- - 3.283E-08 N
181) A circlular capactitor of radius 3.3 m has a gap of 16 mm, and a charge of 68 μC. What is the electric field between the plates?
- - 1.26E+05 N/C (or V/m)
- - 1.53E+05 N/C (or V/m)
- - 1.85E+05 N/C (or V/m)
- + 2.24E+05 N/C (or V/m)
- - 2.72E+05 N/C (or V/m)
182) A circlular capactitor of radius 4.6 m has a gap of 12 mm, and a charge of 77 μC. Compute the surface integral over an inner face of the capacitor.
- - 6.59E-11 Vs2m-1
- - 7.99E-11 Vs2m-1
- + 9.68E-11 Vs2m-1
- - 1.17E-10 Vs2m-1
- - 1.42E-10 Vs2m-1
183) A circlular capactitor of radius 4.6 m has a gap of 11 mm, and a charge of 60 μC. The capacitor is discharged through a 9 kΩ resistor. What is the decay time?
- - 3.28E-04 s
- - 3.97E-04 s
- + 4.82E-04 s
- - 5.83E-04 s
- - 7.07E-04 s
184) A circlular capactitor of radius 4.1 m has a gap of 11 mm, and a charge of 66 μC. The capacitor is discharged through a 6 kΩ resistor. What is what is the maximum magnetic field at the edge of the capacitor? (There are two ways to do this; you should know both.)
- - 6.33E-09 Tesla
- - 7.96E-09 Tesla
- - 1.00E-08 Tesla
- + 1.26E-08 Tesla
- - 1.59E-08 Tesla

- + how a nearsighted person might see a distant object
- - how a nearsighted person might see an object that is too close for comfort
- - how a farsighted person might see an object that is too close for comfort
- - how a farsighted person might see a distant object

- - how a nearsighted person might see a distant object
- - how a farsighted person might see a distant object
- + how a farsighted person might see an object that is too close for comfort
- - how a nearsighted person might see an object that is too close for comfort
187) In optics, normal means
- - to the left of the optical axis
- - parallel to the surface
- + perpendicular to the surface
- - to the right of the optical axis
188) The law of reflection applies to
- - only light in a vacuum
- - telescopes but not microscopes
- - curved surfaces
- + both flat and curved surfaces
- - flat surfaces
189) When light passes from air to glass
- - the frequency decreases
- - the frequency increases
- - it bends away from the normal
- + it bends towards the normal
- - it does not bend
190) When light passes from glass to air
- - it does not bend
- - the frequency decreases
- - the frequency increases
- - it bends towards the normal
- + it bends away from the normal
191) An important principle that allows fiber optics to work is
- - the invariance of the speed of light
- + total internal reflection
- - total external refraction
- - partial internal absorption
- - the Doppler shift
192) The focal point is where
- - rays meet whenever they pass through a lens
- + rays meet if they were parallel to the optical axis before striking a lens
- - rays meet whenever they are forming an image
- - rays meet if they are parallel to each other
- - the center of the lens
193) An object is placed 8 cm to the left of a diverging lens with a focal length of 4.3 cm. How far is the image from the lens?
- + 2.8 x 100 cm
- - 4.97 x 100 cm
- - 8.84 x 100 cm
- - 1.57 x 101 cm
- - 2.8 x 101 cm
194) An object is placed 4.15 cm to the left of a converging lens with a focal length of 3.6 cm. How far is the image from the lens?
- - 8.59 x 100 cm
- - 1.53 x 101 cm
- + 2.72 x 101 cm
- - 4.83 x 101 cm
- - 8.59 x 101 cm
195) An object of height 0.54 cm is placed 131 cm behind a diverging lens with a focal length of 71 cm. What is the height of the image?
- - 9.15 x 10-2 cm
- - 1.1 x 10-1 cm
- - 1.32 x 10-1 cm
- - 1.58 x 10-1 cm
- + 1.9 x 10-1 cm
196) An object is placed 13.2 cm to the left of a diverging lens with a focal length of 17.1 cm. On the side, at a distance of 5.1 cm from the diverging lens is a converging lens with focal length equal to 4 cm. How far is the final image from the converging lens?
- - 1.86 x 10-1 cm
- - 5.87 x 10-1 cm
- - 1.86 x 100 cm
- + 5.87 x 100 cm
- - 1.86 x 101 cm
198) ![]() If this represents the eye looking at an object, where is this object?
If this represents the eye looking at an object, where is this object?
- - One focal length in front of the eye
- + Two (of the other answers) are true
- - very far away
- - at infinity
- - directly in front of the eye (almost touching)
199) After passing through a the lens of a camera or the eye, the focal point is defined as where the rays meet.
- - true
- + false
200) ![]() Mr. Smith is gazing at something as shown in the figure to the left. Suppose he does not refocus, but attempts to stare at the star shown in the figures below. Which diagram depicts how the rays from the star would travel if he does not refocus?
Mr. Smith is gazing at something as shown in the figure to the left. Suppose he does not refocus, but attempts to stare at the star shown in the figures below. Which diagram depicts how the rays from the star would travel if he does not refocus?
201) Your solitaire deck uses ♥ ♠ ♣ and your answer cards are 4 and 5. You select 4♠, 4♣, and 5♥. If the questions were Q♠ and Q♣, you would__
- + lose 3 points
- - lose 1 point
- - win 1 point
- - win 3 points
- - be disqualified for cheating
202) Your solitaire deck uses ♥ ♠ ♣ and your answer cards are 4 and 5. You select 4♠, 5♣, and 5♥. If the questions were Q♠ and Q♣, you would__
- - lose 3 points
- - lose 1 point
- + win 1 point
- - win 3 points
- - be disqualified for cheating
203) You solitaire deck uses ♥ ♠ ♣ and your answer cards are 4 and 5. You select 4♠, 5♣, and 5♥. If the questions were Q♠ and Q♣. Which of the following wins?
- - K♥ and K♠
- - K♠ and K♣
- - K♥ and K♣
- + two of these are true
- - none of these are true
204) You solitaire deck uses ♥ ♠ ♣ and your answer cards are 4 and 5. You select 4♠, 5♣, and 5♥. If the questions were Q♠ and Q♣. Which of the following loses?
- - K♥ and K♠
- - K♠ and K♣
- + K♥ and K♣
- - two of these are true
- - none of these are true
205) If you play the solitaire game 6 times, you will on average win ___ times.
- + 4
- - 2
- - 3
- - 6
- - 5
206) If you play the solitaire game 3 times, you will on average lose ___ times.
- + 1
- - 2
- - 3
- - 4
- - 5
207) If you play the solitaire game 6 times, you will on average lose ___ times.
- - 4
- + 2
- - 3
- - 6
- - 5
208) If you play the solitaire game 3 times, you will on average win ___ times.
- - 1
- + 2
- - 3
- - 4
- - 5
209) The light is linearly polarized, the electric field is oriented ________to the direction of motion
- - parallel
- + perpendicular
- - at 45 degrees
- - all of these are possible
210) Hold a pendulum a moderate distance from equilibrium and release it by tossing it in a direction perpendicular to the displacement of the mass from equilibrium. The resulting polarization will be ____ (pick the best answer)
- - linearly
- - circular
- - circular or linear
- + circular or elliptical
- - linear or elliptical
211) A mathematically pure (strictly monochromatic) __________ wave (oscillation) that is unpolarized cannot be created
- - electromagnetic
- - pendulum
- + electromagnetic or pendulum
- - both can be created
212) To create an unpolarized pendulum oscillation
- - create an elliptically polarized wave with an ε>0.2
- - create an elliptically polarized wave with an ε<0.8
- - create an elliptically polarized wave with an 0.2<ε<0.8
- + start with a linear, circular, or elliptical wave and slowly evolve to different polarizations
213) If the hypotenuse of a 45°-45° right triangle has a length of what is the length of each side?
- -
- -
- -
- +
- -
214) If the hypotenuse of a 45°-45° right triangle has a length of what is the length of each side?
- -
- +
- -
- -
- -
215) If the hypotenuse of a 60°-30° right triangle has a length of 1 what is the length of the shorter side?
- -
- -
- +
- -
- -
216) If the hypotenuse of a 60°-30° right triangle has a length of 1 what is the length of the longer side?
- -
- -
- -
- +
- -
217) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field. By what factor does a filter reduce the electric field if it is oriented 30° to that field?
- -
- -
- -
- +
- -
218) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field. By what factor does a filter reduce the electric field if it is oriented 60° to that field?
- -
- -
- +
- -
- -
219) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field. A 12 mW laser strikes a polarizing filter oriented 30° to the incoming axis of polarization. How much power passes the filter?
- - 3mW
- - 4mW
- - 6mW
- - 8mW
- + 9mW
220) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field.A 12 mW laser strikes a polarizing filter oriented 30° to the incoming axis of polarization. How much power is blocked by the filter?
- + 3mW
- - 4mW
- - 6mW
- - 8mW
- - 9mW
221) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field.A 12 mW laser strikes a polarizing filter oriented 60° to the incoming axis of polarization. How much power is blocked by the filter?
- - 3mW
- - 4mW
- - 6mW
- - 8mW
- + 9mW
222) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field.A 12 mW laser strikes a polarizing filter oriented 60° to the incoming axis of polarization. How much power is passed by the filter?
- + 3mW
- - 4mW
- - 6mW
- - 8mW
- - 9mW
223) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field.A 12 mW laser strikes a polarizing filter oriented 45° to the incoming axis of polarization. How much power is passed by the filter?
- - 3mW
- - 4mW
- + 6mW
- - 8mW
- - 9mW

- - 1/32
- - 1/16
- - 3/32
- + 1/8
- - 3/16
225) Hold a pendulum a moderate distance from equilibrium and release it by tossing it in a direction parallel to the displacement of the mass from equilibrium. The resulting polarization will be ____ (pick the best answer)
- + linearly
- - circular
- - circular or linear
- - circular or elliptical
- - linear or elliptical
226) A linear polarizer selects a component of the electric field. Also, the energy density of light is proportional to the square of the electric field. Unpolarized light impinges on three linear filters. The second is oriented 30° from the first, and the third is rotated by an additional 60°, making it at right angles from the first filter. What fraction of the power incident on the first filter emerges from the last?
- - 1/32
- - 1/16
- + 3/32
- - 1/8
- - 3/16
227) If the wavelength λ associated with a photon is cut in half, the photon's energy E
- - is cut in half
- - is reduced by a factor of 4
- - stays the same
- + becomes twice as big
- - becomes 4 times as big
228) If the wavelength λ associated with a photon doubles, the photon's frequency f
- + is cut in half
- - is reduced by a factor of 4
- - stays the same
- - becomes twice as big
- - becomes 4 times as big
229) If the frequency f associated with a photon increases by a factor of 4, the photon's wavelength λ
- - is cut in half
- + is reduced by a factor of 4
- - stays the same
- - becomes twice as big
- - becomes 4 times as big
230) If the frequency f associated with a photon increases by a factor of 4, the photon's energy E
- - is cut in half
- - is reduced by a factor of 4
- - stays the same
- - becomes twice as big
- + becomes 4 times as big
231) If an atom emits two photons in a cascade emission and both photons have 2 eV of energy, the atom's energy
- - stays the same
- - increases by 2 eV
- - increases by 4 eV
- - decreases by 2 eV
- + decreases by 4 eV
232) If an atom absorbs a photon with 2 eV energy, the atom's energy
- - stays the same
- + increases by 2 eV
- - increases by 4 eV
- - decreases by 2 eV
- - decreases by 4 eV
233) If a 3 eV photon strikes a metal plate and causes an electron to escape, that electron will have a kinetic energy that is
- - zero
- + less than 3 eV
- - equal to 3 eV
- - greater than 3 eV
- - equal to 6 eV
234) In the Phet lab for photoelectric effect, how was the electron's kinetic energy measured?
- - measuring spin
- - measuring polarization
- - measuring both spin and polarization
- - deflecting the electron with a magnetic field
- + stopping the electron with an applied voltage
235) If an atom absorbs a photon with 4 eV energy, the atom's energy
- - stays the same
- - increases by 2 eV
- - increases by 4 eV
- - decreases by 2 eV
- + decreases by 4 eV
236) If 1018 photons pass through a small hole in your roof every second, how many photons would pass through it if you doubled the diameter?
- - 1018
- - 2x1018
- + 4x1018
- - 6x1018
- - 8x1018
237) Two black bodies of are created by cutting identical small holes in two large containers. The holes are oriented so that all the photons leaving one will enter the other. The objects have different temperature and different volume. Which object has the greater electromagnetic ("photon") energy density (energy per unit volume)?
- + The hotter object has a greater energy density.
- - The larger object has a greater energy density.
- - They have the same energy density (since the holes are identical).
- - No unique answer exists because two variables are involved (temperature and volume).
238) Two black bodies of are created by cutting identical small holes two large containers. The holes are oriented so that all the photons leaving one will enter the other. The objects have different temperature and different volume. Which object emits more photons per second (above a given threshold energy)?
- + The object with the greater temperature emits more.
- - The object with the greater volume.
- - They both emit the same number of photons (since the holes are identical).
- - No unique answer exists because two variables are involved (temperature and volume).
239) Two black bodies of are created by cutting identical small holes in two large containers. The holes are oriented so that all the photons leaving one will enter the other. The objects have different temperature and different volume. Which object has the greater electromagnetic ("photon") energy?
- - The hotter object has a greater energy.
- - The larger object has a greater energy.
- - They have the same energy (since the holes are identical).
- + No unique answer exists because two variables are involved (temperature and volume).

- - Photons striking metal and ejecting electrons (photo-electric effect explained in 1905)
- - Diffraction observed in light so faint that photons seemed to have no mechanism to interact with each other (observed in 1909)
- - A system similar to the one that led to the 1901 proposal that light energy is quantized as integral multiples of hf (except that Plank assumed that the walls were conductive.)
- + Evidence presented in 1800 that light is a wave.
- - The transfer of energy and momentum of a high energy photon of a nearly free electron.

- - Photons striking metal and ejecting electrons (photo-electric effect explained in 1905)
- + Diffraction observed in light so faint that photons seemed to have no mechanism to interact with each other (observed in 1909)
- - A system similar to the one that led to the 1901 proposal that light energy is quantized as integral multiples of hf (except that Plank assumed that the walls were conductive.)
- - Evidence presented in 1800 that light is a wave.
- - The transfer of energy and momentum of a high energy photon of a nearly free electron.

- + Photons striking metal and ejecting electrons (photo-electric effect explained in 1905)
- - Diffraction observed in light so faint that photons seemed to have no mechanism to interact with each other (observed in 1909)
- - A system similar to the one that led to the 1901 proposal that light energy is quantized as integral multiples of hf (except that Plank assumed that the walls were conductive.)
- - Evidence presented in 1800 that light is a wave.
- - The transfer of energy and momentum of a high energy photon of a nearly free electron.

- - Photons striking metal and ejecting electrons (photo-electric effect explained in 1905)
- - Diffraction observed in light so faint that photons seemed to have no mechanism to interact with each other (observed in 1909)
- + A system similar to the one that led to the 1901 proposal that light energy is quantized as integral multiples of hf
- - Evidence presented in 1800 that light is a wave.
- - The transfer of energy and momentum of a high energy photon of a nearly free electron.
244) A photon is polarized at 5° when it encounters a filter oriented at 35°. What is the probability that it passes?
- - 0
- - 1/4
- - 1/2
- + 3/4
- - 1
245) A photon is polarized at 10° when it encounters a filter oriented at 55°. What is the probability that it passes?
- - 0
- - 1/4
- + 1/2
- - 3/4
- - 1
246) A photon is polarized at 10° when it encounters a filter oriented at 70°. What is the probability that it passes?
- - 0
- + 1/4
- - 1/2
- - 3/4
- - 1
247) A photon is polarized at 10° when it encounters a filter oriented at 40°. What is the probability that it is blocked?
- - 0
- - 1/4
- - 1/2
- + 3/4
- - 1
248) A photon is polarized at 5° when it encounters a filter oriented at 50°. What is the probability that it is blocked?
- - 0
- - 1/4
- + 1/2
- - 3/4
- - 1
249) A photon is polarized at 5° when it encounters a filter oriented at 65°. What is the probability that it is blocked?
- - 0
- + 1/4
- - 1/2
- - 3/4
- - 1
250) A photon is polarized at 10° when it encounters a filter oriented at 100°. What is the probability that it passes?
- + 0
- - 1/4
- - 1/2
- - 3/4
- - 1
251) A photon is polarized at 10° when it encounters a filter oriented at 100°. What is the probability that it is blocked?
- - 0
- - 1/4
- - 1/2
- - 3/4
- + 1

P(♠,♦) = ?
Assume the dots represent five observations.
- - 2/4=1/2
- - 2/5
- + 3/5
- - 3/4
- - 5/6

P(♠,♥) = ?
Assume the dots represent five observations.
- - 2/4=1/2
- + 2/5
- - 3/5
- - 3/4
- - 5/6

P(♠,♦)+P(♠,♥)+P(♥,♦) = ?
Assume the dots represent five observations.
- - 4/5
- - 5/6
- - 5/4
- - 6/5
- + 7/5

C(♠,♦) = ?
Assume the dots represent five observations.
- - −2/5
- - −1/5
- - 0
- + +1/5
- - +2/5
- - +1

C(♠,♥) = ?
Assume the dots represent five observations.
- - −2/5
- + −1/5
- - 0
- - +1/5
- - +2/5
- - +1

- - 0
- - 1/4
- + 1/2
- - 3/4
- - 1
- - 5/4

- - 0
- - 1/4
- - 1/2
- + 3/4
- - 1
- - 5/4

- - 0
- - 1/4
- - 1/2
- - 3/4
- - 1
- + 5/4





















![{\displaystyle is:{\frac {1}{4\pi \epsilon _{0}}}\int _{\mathcal {A}}^{\mathcal {B}}{\frac {{\mathcal {C}}\;\lambda ds}{\left[{\mathcal {D}}^{2}+{\mathcal {E}}^{2}\right]^{\mathcal {F}}\;}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd4dc107d6ebe6e1a3831cbf4bfe7e68291caf44)




































































































































