WikiJournal of Science/Affine symmetric group

WikiJournal of Science
Open access • Publication charge free • Public peer review • Wikipedia-integrated

Journal issues

Current

Volume 7(1)

Previous
Volume 1(1)
Volume 1(2)
Volume 2(1)
Volume 3(1)
Volume 4(1)
Volume 5(1)
Volume 6(1)

More resources

Articles in review

Editorial guidelines
Ethics statement
Bylaws
Financials
Calendar

Contact

This article has been through public peer review.

Post-publication review comments or direct edits can be left at the version as it appears on Wikipedia.

First submitted: 6 Jun 2020
Accepted: 21 Apr 2021
Reviewer comments

PDF: Download
DOI: 10.15347/WJS/2021.003
QID: Q100400684
XML: Download

Suggested citation format:
Joel B. Lewis (21 April 2021). "Affine symmetric group". WikiJournal of Science 4 (1): 3. doi:10.15347/WJS/2021.003. Wikidata Q100400684. ISSN 2470-6345. https://upload.wikimedia.org/wikiversity/en/7/7c/Affine_symmetric_group.pdf.

Citation metrics
AltMetrics
Page views on Wikipedia

Wikipedia: Content from this work is used in the following Wikipedia article: Affine symmetric group.

License: This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction, provided the original author and source are credited.

Editors:

Jonathan Holland (handling editor) contact
Thomas Shafee contact

Reviewers: (comments)

Martina Balagović
Thomas Kyle Petersen
Brant Jones

Article information

Author: Joel Brewster Lewis^[a]^[i]

See author information ▼

↑ George Washington University

↑ jblewis@gwu.edu

Abstract

The affine symmetric group is a mathematical structure that describes the symmetries of the number line and the regular triangular tesselation of the plane, as well as related higher dimensional objects. It is an infinite extension of the symmetric group, which consists of all permutations (rearrangements) of a finite set. In addition to its geometric description, the affine symmetric group may be defined as the collection of permutations of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. These different definitions allow for the extension of many important properties of the finite symmetric group to the infinite setting, and are studied as part of the fields of combinatorics and representation theory.

Non-technical summary
Flat, straight-edged shapes (like triangles) or 3D ones (like pyramids) have only a finite number of symmetries. In contrast, the affine symmetric group is a way to mathematically describe all the symmetries possible when an infinitely large flat surface is covered by triangular tiles. As with many subjects in mathematics, it can also be thought of in a number of ways: for example, it also describes the symmetries of the infinitely long number line, or the possible arrangements of all integers (..., −2, −1, 0, 1, 2, ...) with certain repetitive patterns. As a result, studying the affine symmetric group extends the study of symmetries of straight-edged shapes or of groups of permutations to the infinite case. It also connects several topics in mathematics that were originally studied for independent reasons, ranging from complex reflection groups to juggling sequences.

Definitions

The affine symmetric group, ${\widetilde {S}}_{n}$ , may be equivalently defined as an abstract group by generators and relations, or in terms of concrete geometric and combinatorial models.

Algebraic definition

In terms of generators and relations, ${\widetilde {S}}_{n}$ is generated by a set $s_{0},s_{1},\ldots ,s_{n-1}$ of $n$ elements that satisfy the following relations: when $n\geq 3$ ,

$s_{i}^{2}=1$ (the generators are involutions),
$s_{i}s_{j}=s_{j}s_{i}$ if $j$ is not one of $i-1,i,i+1$ , and
$s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}$ .

In the relations above, indices are taken modulo $n$ , so that the third relation includes as a particular case $s_{0}s_{n-1}s_{0}=s_{n-1}s_{0}s_{n-1}$ . (The second and third relation are sometimes called the braid relations.) When $n=2$ , the affine symmetric group ${\widetilde {S}}_{2}$ is the infinite dihedral group generated by two elements $s_{0},s_{1}$ subject only to the relations $s_{0}^{2}=s_{1}^{2}=1$ .^[1]

This definition endows ${\widetilde {S}}_{n}$ with the structure of a Coxeter group, with the $s_{i}$ as Coxeter generating set. For $n\geq 3$ , its Coxeter–Dynkin diagram is the $n$ -cycle, while for $n=2$ it consists of two nodes joined by an edge labeled $\infty$ .^[2]

Geometric definition

In the Euclidean space $\mathbb {R} ^{n}$ with coordinates $(x_{1},\ldots ,x_{n})$ , the set $V$ of points that satisfy the equation $x_{1}+x_{2}+\ldots +x_{n}=0$ forms a (hyper)plane (an $(n - 1)$ -dimensional subspace). For every pair of distinct elements $i$ and $j$ of $\{1,\ldots ,n\}$ and every integer $k$ , the set of points in $V$ that satisfy $x_{i}-x_{j}=k$ forms a plane in $V$ , and there is a unique reflection of $V$ that fixes this plane. Then the affine symmetric group can be realized geometrically as the collection of all maps from $V$ to itself that arise by composing several of these reflections.^[3]

Inside $V$ , the type A root lattice $Λ$ is the subset of points with integer coordinates, that is, it is the set of all the integer vectors $(a_{1},\ldots ,a_{n})$ such that $a_{1}+\ldots +a_{n}=0$ . Each of the reflections preserves this lattice, and so the lattice is preserved by the whole group. In fact, one may define ${\widetilde {S}}_{n}$ to be the group of rigid transformations of $V$ that preserve the lattice $Λ$ .

These reflecting planes divide the space $V$ into congruent simplicies, called alcoves.^[4] The situation when $n=3$ is shown at right; in this case, the root lattice is a triangular lattice, and the reflecting lines divide the plane into equilateral triangular alcoves. (For larger $n$ , the alcoves are not regular simplices.)

To translate between the geometric and algebraic definitions, fix an alcove and consider the $n$ hyperplanes that form its boundary. For example, there is a unique alcove (the fundamental alcove) consisting of points $(x_{1},\ldots ,x_{n})$ such that $x_{1}\geq x_{2}\geq \dots \geq x_{n}\geq x_{1}-1$ , which is bounded by the hyperplanes $x_{1}-x_{2}=0$ , $x_{2}-x_{3}=0$ , ..., and $x_{1}-x_{n}=1$ . (This is illustrated in the case $n=3$ at right.) For $i=1,\ldots ,n-1$ , one may identify the reflection through $x_{i}-x_{i+1}=0$ with the Coxeter generator $s_{i}$ , and also identify the reflection through $x_{1}-x_{n}=1$ with the generator $s_{0}=s_{n}$ .^[4]

Combinatorial definition

The affine symmetric group may be realized as a group of periodic permutations of the integers. In particular, say that a bijection $u\colon \mathbb {Z} \to \mathbb {Z}$ is an affine permutation if $u(x+n)=u(x)+n$ for all integers $x$ and $u(1)+u(2)+\ldots +u(n)=1+2+\ldots +n$ . (It is a consequence of the first property that the numbers $u(1),\ldots ,u(n)$ must all be distinct modulo $n$ .) Such a function is uniquely determined by its window notation $[u(1),\ldots ,u(n)]$ , and so affine permutations may also be identified with tuples $[u(1),\ldots ,u(n)]$ of integers that contain one element from each congruence class modulo $n$ and sum to $1+2+\ldots +n$ .^[5]

To translate between the combinatorial and algebraic definitions, for $i=1,\ldots ,n-1$ one may identify the Coxeter generator $s_{i}$ with the affine permutation that has window notation $[1,2,\ldots ,i-1,i+1,i,i+2,\ldots ,n]$ , and also identify the generator $s_{0}=s_{n}$ with the affine permutation $[0,2,3,\ldots ,n-2,n-1,n+1]$ . More generally, every reflection (that is, a conjugate of one of the Coxeter generators) can be described uniquely as follows: for distinct integers $i$ , $j$ in $\{1,\ldots ,n\}$ and arbitrary integer $k$ , it maps $i$ to $j - kn$ , maps $j$ to $i + kn$ , and fixes all inputs not congruent to $i$ or $j$ modulo $n$ .^[6] (In terms of the geometric definition, this corresponds to the reflection across the plane $x_{i}-x_{j}=k$ . The correspondence between the geometric and combinatorial representations for other elements is discussed below.)

Representation as matrices

One may represent affine permutations as infinite periodic permutation matrices.^[7] If $u:\mathbb {Z} \to \mathbb {Z}$ is an affine permutation, one places the entry 1 at position $(i,u(i))$ in the infinite grid $\mathbb {Z} \times \mathbb {Z}$ for each integer $i$ , and all other entries are equal to 0. Since $u$ is a bijection, the resulting matrix contains exactly one 1 in every row and column. The periodicity condition on the map $u$ ensures that the entry at position $(a,b)$ is equal to the entry at position $(a+n,b+n)$ for every pair of integers $(a,b)$ . For example, a portion of matrix for the affine permutation $[2,0,4]\in {\widetilde {S}}_{3}$ is shown below, with the conventions that 1s are replaced by •, 0s are omitted, rows numbers increase from top to bottom, column numbers increase from left to right, and the boundary of the box consisting of rows and columns 1, 2, 3 is drawn: ${\begin{array}{ccc|ccc|ccc}&\bullet &&&&&&&\\&&&&&&&&\\&&&\bullet &&&&&\\\hline &&&&\bullet &&&&\\&&\bullet &&&&&&\\&&&&&&\bullet &&\\\hline &&&&&&&\bullet &\\&&&&&\bullet &&&\end{array}}$

Relationship to the finite symmetric group

The affine symmetric group ${\widetilde {S}}_{n}$ contains the finite symmetric group $S_{n}$ as both a subgroup and a quotient.

As a subgroup

There is a canonical way to choose a subgroup of ${\widetilde {S}}_{n}$ that is isomorphic to the finite symmetric group $S_{n}$ . In terms of the algebraic definition, this is the subgroup of ${\widetilde {S}}_{n}$ generated by $s_{1},\ldots ,s_{n-1}$ (excluding the simple reflection $s_{0}=s_{n}$ ). Geometrically, this corresponds to the subgroup of transformations that fix the origin, while combinatorially it corresponds to the window notations for which $\{u(1),\ldots ,u(n)\}=\{1,2,\ldots ,n\}$ (that is, in which the window notation is the one-line notation of a finite permutation).^[8]^[3]

If $u=[u(1),u(2),\ldots ,u(n)]$ is the window notation of an element of this standard copy of $S_{n}\subset {\widetilde {S}}_{n}$ , its action on the hyperplane $V$ in $\mathbb {R} ^{n}$ is given by permutation of coordinates: $(x_{1},x_{2},\ldots ,x_{n})\cdot u=(x_{u(1)},x_{u(2)},\ldots ,x_{u(n)})$ . (In this article, the geometric action of permutations and affine permutations is on the right; thus, if $u$ and $v$ are two affine permutations, the action of $uv$ on a point is given by first applying $u$ , then applying $v$ .)

There are also many nonstandard copies of $S_{n}$ contained in ${\widetilde {S}}_{n}$ . A geometric construction is to pick any point $a$ in $Λ$ (that is, an integer vector whose coordinates sum to 0); the subgroup $({\widetilde {S}}_{n})_{a}$ of ${\widetilde {S}}_{n}$ of isometries that fix $a$ is isomorphic to $S_{n}$ . The analogous combinatorial construction is to choose any subset $A$ of $\mathbb {Z}$ that contains one element from each conjugacy class modulo $n$ and whose elements sum to $1+2+\ldots +n$ ; the subgroup $({\widetilde {S}}_{n})_{A}$ of ${\widetilde {S}}_{n}$ of affine permutations that stabilize $A$ is isomorphic to $S_{n}$ .

As a quotient

There is a simple map (technically, a surjective group homomorphism) $π$ from ${\widetilde {S}}_{n}$ onto the finite symmetric group $S_{n}$ . In terms of the combinatorial definition, it is to reduce the window entries modulo $n$ to elements of $\{1,2,\ldots ,n\}$ , leaving the one-line notation of a permutation. The image $\pi (u)$ of an affine permutation $u$ is called the underlying permutation of $u$ .

The map $π$ sends the Coxeter generator $s_{0}=[0,2,3,4,\ldots ,n-2,n-1,n+1]$ to the permutation whose one-line notation and cycle notation are $[n,2,3,4,\ldots ,n-2,n-1,1]$ and $(1\;n)$ , respectively. In terms of the Coxeter generators of $S_{n}$ , this can be written as $\pi (s_{0})=s_{1}s_{2}\cdots s_{n-2}s_{n-1}s_{n-2}\cdots s_{2}s_{1}$ .

The kernel $π$ is the set of affine permutations whose underlying permutation is the identity. The window notations of such affine permutations are of the form $[1-a_{1}\cdot n,2-a_{2}\cdot n,\ldots ,n-a_{n}\cdot n]$ , where $(a_{1},a_{2},\ldots ,a_{n})$ is an integer vector such that $a_{1}+a_{2}+\ldots +a_{n}=0$ , that is, where $(a_{1},\ldots ,a_{n})\in \Lambda$ . Geometrically, this kernel consists of the translations, that is, the isometries that shift the entire space $V$ without rotating or reflecting it. In an abuse of notation, the symbol $Λ$ is used in this article for all three of these sets (integer vectors in $V$ , affine permutations with underlying permutation the identity, and translations); in all three settings, the natural group operation turns $Λ$ into an abelian group, generated freely by the $n - 1$ vectors $\{(1,-1,0,\ldots ,0),(0,1,-1,\ldots ,0),\ldots ,(0,\ldots ,0,1,-1)\}$ .

Connection between the geometric and combinatorial definitions

The subgroup $Λ$ is a normal subgroup of ${\widetilde {S}}_{n}$ , and one has an isomorphism ${\widetilde {S}}_{n}\cong S_{n}\ltimes \Lambda$ between ${\widetilde {S}}_{n}$ and the semidirect product of the finite symmetric group $S_{n}$ with $Λ$ , where the action of $S_{n}$ on $Λ$ is by permutation of coordinates. Consequently, identifying the finite symmetric group $S_{n}$ as its standard copy in ${\widetilde {S}}_{n}$ , one has that every element $u$ of ${\widetilde {S}}_{n}$ may be realized uniquely as a product $u=r\cdot t$ where $r\in S_{n}$ is a finite permutation and $t\in \Lambda$ .

This point of view allows for a direct translation between the combinatorial and geometric definitions of ${\widetilde {S}}_{n}$ : if one writes $[u(1),\ldots ,u(n)]=[r_{1}-a_{1}\cdot n,\ldots ,r_{n}-a_{n}\cdot n]$ where $r=[r_{1},\ldots ,r_{n}]=\pi (u)$ and $(a_{1},a_{2},\ldots ,a_{n})\in \Lambda$ then the affine permutation $u$ corresponds to the rigid motion of $V$ defined by $(x_{1},\ldots ,x_{n})\cdot u=\left(x_{r(1)}+a_{1},\ldots ,x_{r(n)}+a_{n}\right).$

Furthermore, as with every affine Coxeter group, the affine symmetric group acts transitively and freely on the set of alcoves. Hence, by making an arbitrary choice of alcove $A_{0}$ , one may place the group in one-to-one correspondence with the alcoves: the identity element corresponds to $A_{0}$ , and every other group element $g$ corresponds to the alcove $A=A_{0}\cdot g$ that is the image of $A_{0}$ under the action of $g$ . This identification for ${\widetilde {S}}_{3}$ is illustrated at right.

Example: $n = 2$

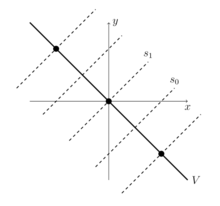
Algebraically, ${\widetilde {S}}_{2}$ is the infinite dihedral group, generated by two generators $s_{0},s_{1}$ subject to the relations $s_{0}^{2}=s_{1}^{2}=1$ . Every other element of the group can be written as an alternating product of copies of $s_{0}$ and $s_{1}$ .

Combinatorially, the affine permutation $s_{1}$ has window notation $[2,1]$ , corresponding to the bijection $2k\mapsto 2k-1,2k-1\mapsto 2k$ for every integer $k$ . The affine permutation $s_{0}$ has window notation $[0,3]$ , corresponding to the bijection $2k\mapsto 2k+1,2k+1\mapsto 2k$ for every integer $k$ . Other elements have the following window notations:

$\overbrace {s_{0}s_{1}\cdots s_{0}s_{1}} ^{2k\,{\text{factors}}}=[1+2k,2-2k]$ ,
$\overbrace {s_{1}s_{0}\cdots s_{1}s_{0}} ^{2k\,{\text{factors}}}=[1-2k,2+2k]$ ,
$\overbrace {s_{0}s_{1}\cdots s_{0}} ^{2k+1\,{\text{factors}}}=[2+2k,1-2k]$ ,
$\overbrace {s_{1}s_{0}\cdots s_{1}} ^{2k+1\,{\text{factors}}}=[2-2(k+1),1+2(k+1)]$ .

Geometrically, the space $V$ is the line with equation $x+y=0$ in the Euclidean plane $\mathbb {R} ^{2}$ . The root lattice inside $V$ consists of those pairs $(a,-a)$ for integral $a$ . The Coxeter generator $s_{1}$ acts on $V$ by reflection across the line $x=y$ (that is, across the origin); the generator $s_{0}$ acts on $V$ by reflection across the line $x=y+1$ (that is, across the point $\left({\tfrac {1}{2}},-{\tfrac {1}{2}}\right)$ . It is natural to identify the line $V$ with the real line $\mathbb {R} ^{1}$ , by sending the point $(x,-x)$ to the real number $2 x$ . With this identification, the root lattice consists of the even integers; the fundamental alcove is the interval $[0, 1]$ ; the element $(s_{1}s_{0})^{k}$ acts by translation by $k$ for any integer $k$ ; and the reflection $s_{1}(s_{0}s_{1})^{k}$ reflects across the point $- k$ for any integer $k$ .

Permutation statistics and permutation patterns

Many permutation statistics and other features of the combinatorics of finite permutations can be extended to the affine case.

Descents, length, and inversions

The length $\ell (g)$ of an element $g$ of a Coxeter group $G$ is the smallest number $k$ such that $g$ can be written as a product $g=s_{i_{1}}\cdots s_{i_{k}}$ of $k$ Coxeter generators of $G$ .^[9]

Geometrically, the length of an element $g$ in ${\widetilde {S}}_{n}$ is the number of reflecting hyperplanes that separate $A_{0}$ and $A_{0}\cdot g$ , where $A_{0}$ is the fundamental alcove (the simplex bounded by the reflecting hyperplanes of the Coxeter generators $s_{0},s_{1},\ldots ,s_{n-1}$ ). (In fact, the same is true for any affine Coxeter group.)^[10]

Combinatorially, the length of an affine permutation is encoded in terms of an appropriate notion of inversions. In particular, one has for an affine permutation $u$ that^[11] $\ell (u)=\#\left\{(i,j)\colon i\in \{1,\ldots ,n\},i<j,{\text{ and }}u(i)>u(j)\right\}.$ Alternatively, it is the number of equivalence classes of pairs $(i,j)\in \mathbb {Z} \times \mathbb {Z}$ such that $i<j$ and $u(i)>u(j)$ under the equivalence relation $(i,j)\equiv (i',j')$ if $(i-i',j-j')=(kn,kn)$ for some integer $k$ .

The generating function for length in ${\widetilde {S}}_{n}$ is^[12]^[13] $\sum _{g\in {\widetilde {S}}_{n}}q^{\ell (g)}={\frac {1-q^{n}}{(1-q)^{n}}}.$

Similarly, one may define an affine analogue of descents in permutations: say that an affine permutation $u$ has a descent in position $i$ if $u(i)>u(i+1)$ . (By periodicity, $u$ has a descent in position $i$ if and only if it has a descent in position $i+kn$ for all integers $k$ .)^[14]

Algebraically, the descents corresponds to the right descents in the sense of Coxeter groups; that is, $i$ is a descent of $u$ if and only if $\ell (u\cdot s_{i})<\ell (u)$ .^[14] The left descents (that is, those indices $i$ such that $\ell (s_{i}\cdot u)<\ell (u)$ are the descents of the inverse affine permutation $u^{-1}$ ; equivalently, they are the values $i$ such that $i$ occurs before $i - 1$ in the sequence $\ldots ,u(-2),u(-1),u(0),u(1),u(2),\ldots$ .

Geometrically, $i$ is a descent of $u$ if and only if the fixed hyperplane of $s_{i}$ separates the alcoves $A_{0}$ and $A_{0}\cdot u$ .

Because there are only finitely many possibilities for the number of descents of an affine permutation, but infinitely many affine permutations, it is not possible to naively form a generating function for affine permutations by number of descents (an affine analogue of Eulerian polynomials).^[15] One possible resolution is to consider affine descents (equivalently, cyclic descents) in the finite symmetric group $S_{n}$ .^[16] Another is to consider simultaneously the length and number of descents of an affine permutation. The generating function for these statistics over ${\widetilde {S}}_{n}$ simultaneously for all $n$ is $\sum _{n\geq 1}{\frac {x^{n}}{1-q^{n}}}\sum _{w\in {\widetilde {S}}_{n}}t^{\operatorname {des} (w)}q^{\ell (w)}=\left[{\frac {x\cdot {\frac {\partial }{\partial {x}}}\log(\exp(x;q))}{1-t\exp(x;q)}}\right]_{x\mapsto x{\frac {1-t}{1-q}}}$ where $des(w)$ is the number of descents of the affine permutation $w$ and $\exp(x;q)=\sum _{n\geq 0}{\frac {x^{n}(1-q)^{n}}{(1-q)(1-q^{2})\cdots (1-q^{n})}}$ is the $q$ -exponential function.^[17]

Cycle type and reflection length

Any bijection $u:\mathbb {Z} \to \mathbb {Z}$ partitions the integers into a (possibly infinite) list of (possibly infinite) cycles: for each integer $i$ , the cycle containing $i$ is the sequence $(\ldots ,u^{-2}(i),u^{-1}(i),i,u(i),u^{2}(i),\ldots )$ where exponentiation represents functional composition. For example, the affine permutation in ${\widetilde {S}}_{5}$ with window notation $[6,3,2,0,4]$ contains the two infinite cycles $(\ldots ,-9,-4,1,6,11,\ldots )$ and $(\ldots ,10,9,5,4,0,-1,-5\ldots )$ as well as infinitely many finite cycles $(5k+2,5k+3)$ for each $k\in \mathbb {Z}$ . Cycles of an affine permutation correspond to cycles of the underlying permutation in an obvious way: in the example above, with underlying permutation $[1,3,2,5,4]=(1)(23)(45)$ , the first infinite cycle corresponds to the cycle (1), the second corresponds to the cycle (45), and the finite cycles all correspond to the cycle (23).

For an affine permutation $u$ , the following conditions are equivalent: all cycles of $u$ are finite, $u$ has finite order, and the geometric action of $u$ on the space $V$ has at least one fixed point.^[18]

The reflection length $\ell _{R}(u)$ of an element $u$ of ${\widetilde {S}}_{n}$ is the smallest number $k$ such that there exist reflections $r_{1},\ldots ,r_{k}$ such that $u=r_{1}\cdots r_{k}$ . (In the symmetric group, reflections are transpositions, and the reflection length of a permutation $u$ is $n-c(u)$ , where $c(u)$ is the number of cycles of $u$ .^[19]) In (Lewis et al. 2019), the following formula was proved for the reflection length of an affine permutation $u$ : for each cycle of $u$ , define the weight to be the integer k such that consecutive entries congruent modulo $n$ differ by exactly $kn$ . (For example, in the permutation $[6,3,2,0,4]$ above, the first infinite cycle has weight 1 and the second infinite cycle has weight −1; all finite cycles have weight 0.) Form a tuple of cycle weights of $u$ (counting translates of the same cycle by multiples of $n$ only once), and define the nullity $\nu (u)$ to be the size of the smallest set partition of this tuple so that each part sums to 0. (In the example above, the tuple is $(1,-1,0)$ and the nullity is 2, since one can take the partition $(1,-1),(0)$ .) Then the reflection length of $u$ is $\ell _{R}(u)=n-2\nu (u)+c(\pi (u)),$ where $\pi (u)$ is the underlying permutation of $u$ .^[20]

For every affine permutation $u$ , there is a choice of subgroup $W$ of ${\widetilde {S}}_{n}$ such that $W\cong S_{n}$ , ${\widetilde {S}}_{n}=W\ltimes \Lambda$ , and for the standard form $u=w\cdot t$ implied by this semidirect product, one has $\ell _{R}(u)=\ell _{R}(w)+\ell _{R}(t)$ .^[21]

Fully commutative elements and pattern avoidance

A reduced word for an element $g$ of a Coxeter group is a tuple $(s_{i_{1}},\ldots ,s_{i_{\ell (g)}})$ of Coxeter generators of minimum possible length such that $g=s_{i_{1}}\cdots s_{i_{\ell (g)}}$ .^[9] The element $g$ is called fully commutative if one can transform any reduced word into any other by sequentially swapping pairs of factors that commute.^[22] For example, in the finite symmetric group $S_{4}$ , the element $2143=(12)(34)$ is fully commutative, since its two reduced words $(s_{1},s_{3})$ and $(s_{3},s_{1})$ can be connected by swapping commuting factors, but $3214=(13)(2)(4)$ is not fully commutative because there is no way to reach the reduced word $(s_{2},s_{1},s_{2})$ starting from the reduced word $(s_{1},s_{2},s_{1})$ by commutations.

Billey, Jockusch & Stanley (1993) proved that in the finite symmetric group $S_{n}$ , a permutation is fully commutative if and only if it avoids the permutation pattern 321, that is, if and only if its one-line notation contains no three-term decreasing subsequence. In (Green 2002), this result was extended to affine permutations: an affine permutation $u$ is fully commutative if and only if there do not exist integers $i<j<k$ such that $u(i)>u(j)>u(k)$ .^[a]

It has also been shown that the number of affine permutations avoiding a single pattern $p$ is finite if and only if $p$ avoids the pattern 321,^[24] so in particular there are infinitely many fully commutative affine permutations. These were enumerated by length in (Hanusa & Jones 2010).

Parabolic subgroups and other structures

The parabolic subgroups of ${\widetilde {S}}_{n}$ and their coset representatives offer a rich combinatorial structure. Other aspects of the affine symmetric group, such as its Bruhat order and representation theory, may also be understood via combinatorial models.

Parabolic subgroups, coset representatives

A standard parabolic subgroup of a Coxeter group is a subgroup generated by a subset of its Coxeter generating set. The maximal parabolic subgroups are those that come from omitting a single Coxeter generator. In ${\widetilde {S}}_{n}$ , all maximal parabolic subgroups are isomorphic to the finite symmetric group $S_{n}$ . The subgroup generated by the subset $\{s_{0},\ldots ,s_{n-1}\}\smallsetminus \{s_{i}\}$ consists of those affine permutations that stabilize the interval $[i+1,i+n]$ , that is, that map every element of this interval to another element of the interval.^[14]

The non-maximal parabolic subgroups of ${\widetilde {S}}_{n}$ are all isomorphic to parabolic subgroups of $S_{n}$ , that is, to a Young subgroup $S_{a_{1}}\times \cdots \times S_{a_{k}}$ for some positive integers $a_{1},\ldots ,a_{k}$ with sum $n$ .

For a fixed element $i$ of $\{0,\ldots ,n-1\}$ , let $J=\{s_{0},\ldots ,s_{n-1}\}\smallsetminus \{s_{i}\}$ be the maximal proper subset of Coxeter generators omitting $s_{i}$ , and let $({\widetilde {S}}_{n})_{J}$ denote the parabolic subgroup generated by $J$ . Every coset $g\cdot ({\widetilde {S}}_{n})_{J}$ has a unique element of minimum length. The collection of such representatives, denoted $({\widetilde {S}}_{n})^{J}$ , consists of the following affine permutations:^[14] $({\widetilde {S}}_{n})^{J}=\left\{u\in {\widetilde {S}}_{n}\colon u(i-n+1)<u(i-n+2)<\ldots <u(i-1)<u(i)\right\}.$

In the particular case that $J=\{s_{1},\ldots ,s_{n-1}\}$ , so that $({\widetilde {S}}_{n})_{J}\cong S_{n}$ is the standard copy of $S_{n}$ inside ${\widetilde {S}}_{n}$ , the elements of $({\widetilde {S}}_{n})^{J}\cong {\widetilde {S}}_{n}/S_{n}$ may naturally be represented by abacus diagrams: the integers are arranged in an infinite strip of width $n$ , increasing sequentially along rows and then from top to bottom; integers are circled if they lie directly above one of the window entries of the minimal coset representative. For example, the minimal coset representative $u=[-5,0,6,9]$ is represented by the abacus diagram at right. To compute the length of the representative from the abacus diagram, one adds up the number of uncircled numbers that are smaller than the last circled entry in each column. (In the example shown, this gives $5+3+0+1=9$ .)^[25]

Other combinatorial models of minimum-length coset representatives for ${\widetilde {S}}_{n}/S_{n}$ can be given in terms of core partitions (integer partitions in which no hook length is divisible by $n$ ) or bounded partitions (integer partitions in which no part is larger than $n - 1$ ). Under these correspondences, it can be shown that the weak Bruhat order on ${\widetilde {S}}_{n}/S_{n}$ is isomorphic to a certain subposet of Young's lattice.^[26]^[27]

Bruhat order

The Bruhat order on ${\widetilde {S}}_{n}$ has the following combinatorial realization. If $u$ is an affine permutation and $i$ and $j$ are integers, define $u[i,j]$ to be the number of integers $a$ such that $a\leq i$ and $u(a)\geq j$ . (For example, with $u=[2,0,4]\in {\widetilde {S}}_{3}$ , one has $u[3,1]=3$ : the three relevant values are $a=0,1,3$ , which are respectively mapped by $u$ to 1, 2, and 4.) Then for two affine permutations $u$ , $v$ , one has that $u\leq v$ in Bruhat order if and only if $u[i,j]\leq v[i,j]$ for all integers $i$ , $j$ .^[28]

Representation theory and an affine Robinson–Schensted correspondence

In the finite symmetric group, the Robinson–Schensted correspondence gives a bijection between the group and pairs $(P,Q)$ of standard Young tableaux of the same shape. This bijection plays a central role in the combinatorics and the representation theory of the symmetric group. For example, in the language of Kazhdan–Lusztig theory, two permutations lie in the same left cell if and only if their images under Robinson–Schensted have the same tableau $Q$ , and in the same right cell if and only if their images have the same tableau $P$ . In (Shi 1986), J.-Y. Shi showed that left cells for ${\widetilde {S}}_{n}$ are indexed instead by tabloids,^[b] and in (Shi 1991) he gave an algorithm to compute the tabloid analogous to the tableau $P$ for an affine permutation. In (Chmutov, Pylyavskyy & Yudovina 2018), the authors extended Shi's work to give a bijective map between ${\widetilde {S}}_{n}$ and triples $(P,Q,\rho )$ consisting of two tabloids of the same shape and an integer vector whose entries satisfy certain inequalities. Their procedure uses the matrix representation of affine permutations and generalizes the shadow construction of Viennot (1977).

Inverse realizations

In some situations, one may wish to consider the action of the affine symmetric group on $\mathbb {Z}$ or on alcoves that is inverse to the one given above.^[c] We describe these alternate realizations now.

In the combinatorial action of ${\widetilde {S}}_{n}$ on $\mathbb {Z}$ , the generator $s_{i}$ acts by switching the values $i$ and $i + 1$ . In the inverse action, it instead switches the entries in positions $i$ and $i + 1$ . Similarly, the action of a general reflection will be to switch the entries at positions $j - kn$ and $i + kn$ for each $k$ , fixing all inputs at positions not congruent to $i$ or $j$ modulo $n$ .^[29] (In the finite symmetric group $S_{n}$ , the analogous distinction is between the active and passive forms of a permutation.^[30])

In the geometric action of ${\widetilde {S}}_{n}$ , the generator $s_{i}$ acts on an alcove $A$ by reflecting it across one of the bounding planes of the fundamental alcove $A 0$ . In the inverse action, it instead reflects $A$ across one of its own bounding planes. From this perspective, a reduced word corresponds to an alcove walk on the tesselated space $V$ .^[31]

Relationship to other mathematical objects

The affine symmetric group is closely related to a variety of other mathematical objects.

Juggling patterns

The juggling pattern 441 visualized as an arc diagram: the height of each throw corresponds to the length of an arc; the two colors of nodes are the left and right hands of the juggler. This pattern has four crossings, which repeat periodically.

In (Ehrenborg & Readdy 1996), a correspondence is given between affine permutations and juggling patterns encoded in a version of siteswap notation.^[32] Here, a juggling pattern of period $n$ is a sequence $(a_{1},\ldots ,a_{n})$ of nonnegative integers (with certain restrictions) that captures the behavior of balls thrown by a juggler, where the number $a_{i}$ indicates the length of time the $i$ th throw spends in the air (equivalently, the height of the throw).^[d] The number $b$ of balls in the pattern is the average $b={\frac {a_{1}+\ldots +a_{n}}{n}}$ .^[34] The Ehrenborg–Readdy correspondence associates to each juggling pattern ${\bf {a}}=(a_{1},\ldots ,a_{n})$ of period $n$ the function $w_{\bf {a}}\colon \mathbb {Z} \to \mathbb {Z}$ defined by $w_{\bf {a}}(i)=i+a_{i}-b,$ where indices of the sequence a are taken modulo $n$ . Then $w_{\bf {a}}$ is an affine permutation in ${\widetilde {S}}_{n}$ , and moreover every affine permutation arises from a juggling pattern in this way.^[32] Under this bijection, the length of the affine permutation is encoded by a natural statistic in the juggling pattern: one has $\ell (w_{\bf {a}})=(b-1)n-\operatorname {cross} ({\bf {a}}),$ where $\operatorname {cross} ({\bf {a}})$ is the number of crossings (up to periodicity) in the arc diagram of a. This allows an elementary proof of the generating function for affine permutations by length.^[35]

For example, the juggling pattern 441 (illustrated at right) has $n=3$ and $b={\frac {4+4+1}{3}}=3$ . Therefore, it corresponds to the affine permutation $w_{441}=[1+4-3,2+4-3,3+1-3]=[2,3,1]$ . The juggling pattern has four crossings, and the affine permutation has length $\ell (w_{441})=(3-1)\cdot 3-4=2$ .

Similar techniques can be used to derive the generating function for minimal coset representatives of ${\widetilde {S}}_{n}/S_{n}$ by length.^[36]

Complex reflection groups

In a finite-dimensional real inner product space, a reflection is a linear transformation that fixes a linear hyperplane pointwise and negates the vector orthogonal to the plane. This notion may be extended to vector spaces over other fields. In particular, in a complex inner product space, a reflection is a unitary transformation $T$ of finite order that fixes a hyperplane.^[e] This implies that the vectors orthogonal to the hyperplane are eigenvectors of $T$ , and the associated eigenvalue is a complex root of unity. A complex reflection group is a finite group of linear transformations on a complex vector space generated by reflections.

The complex reflection groups were fully classified by Shephard & Todd (1954): each complex reflection group is isomorphic to a product of irreducible complex reflection groups, and every irreducible either belongs to an infinite family $G(m,p,n)$ (where $m$ , $p$ , and $n$ are positive integers such that $p$ divides $m$ ) or is one of 34 other (so-called "exceptional") examples. The group $G(m,1,n)$ is the generalized symmetric group: algebraically, it is the wreath product $(\mathbb {Z} /m\mathbb {Z} )\wr S_{n}$ of the cyclic group $\mathbb {Z} /m\mathbb {Z}$ with the symmetric group $S_{n}$ . Concretely, the elements of the group may be represented by monomial matrices (matrices having one nonzero entry in every row and column) whose nonzero entries are all $m$ th roots of unity. The groups $G(m,p,n)$ are subgroups of $G(m,1,n)$ , and in particular the group $G(m,m,n)$ consists of those matrices in which the product of the nonzero entries is equal to 1.

In (Shi 2002), Shi showed that the affine symmetric group is a generic cover of the family $\left\{G(m,m,n)\colon m\geq 1\right\}$ , in the following sense: for every positive integer $m$ , there is a surjection $\pi _{m}$ from ${\widetilde {S}}_{n}$ to $G(m,m,n)$ , and these maps are compatible with the natural surjections $G(m,m,n)\twoheadrightarrow G(p,p,n)$ when $p\mid m$ that come from raising each entry to the $m / p$ th power. Moreover, these projections respect the reflection group structure, in that the image of every reflection in ${\widetilde {S}}_{n}$ under $\pi _{m}$ is a reflection in $G(m,m,n)$ ; and similarly when $m>1$ the image of the standard Coxeter element $s_{0}\cdot s_{1}\cdots s_{n-1}$ in ${\widetilde {S}}_{n}$ is a Coxeter element in $G(m,m,n)$ .^[37]

Affine Lie algebras

Each affine Coxeter group is associated to an affine Lie algebra, a certain infinite-dimensional non-associative algebra with unusually nice representation-theoretic properties. In this association, the Coxeter group arises as a group of symmetries of the root space of the Lie algebra (the dual of the Cartan subalgebra).^[38] In the classification of affine Lie algebras, the one associated to ${\widetilde {S}}_{n}$ is of (untwisted) type $A_{n-1}^{(1)}$ , with Cartan matrix ${\begin{bmatrix}2&-2\\-2&2\end{bmatrix}}$ for $n=2$ and ${\begin{bmatrix}2&-1&0&\cdots &0&-1\\-1&2&-1&\cdots &0&0\\0&-1&2&\cdots &0&0\\\vdots &\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&0&\cdots &2&-1\\-1&0&0&\cdots &-1&2\end{bmatrix}}$ (a circulant matrix) for $n>2$ .^[39]

Like other Kac–Moody algebras, affine Lie algebras satisfy the Weyl–Kac character formula, which expresses the characters of the algebra in terms of their highest weights.^[40] In the case of affine Lie algebras, the resulting identities are equivalent to the Macdonald identities. In particular, for the affine Lie algebra of type $A_{1}^{(1)}$ , associated to the affine symmetric group ${\widetilde {S}}_{2}$ , the corresponding Macdonald identity is equivalent to the Jacobi triple product.^[41]

Extended affine symmetric group

The affine symmetric group is a subgroup of the extended affine symmetric group. The extended group is isomorphic to the wreath product $\mathbb {Z} \wr S_{n}$ . Its elements are extended affine permutations: bijections $u\colon \mathbb {Z} \to \mathbb {Z}$ such that $u(x+n)=u(x)+n$ for all integers $x$ . Unlike the affine symmetric group, the extended affine symmetric group is not a Coxeter group. However, it has a natural generating set that extends the Coxeter generating set for ${\widetilde {S}}_{n}$ : the shift operator $\tau$ whose window notation is $\tau =[2,3,\ldots ,n,n+1]$ generates the extended group with the simple reflections, subject to the additional relations $\tau s_{i}\tau ^{-1}=s_{i+1}$ .^[7]

Combinatorics of other affine Coxeter groups

The geometric action of the affine symmetric group ${\widetilde {S}}_{n}$ places it naturally in the family of affine Coxeter groups, all of which have a similar geometric action. The combinatorial description of the ${\widetilde {S}}_{n}$ may also be extended to many of these groups: in (Eriksson & Eriksson 1998), an axiomatic description is given of certain permutation groups acting on $\mathbb {Z}$ (the "George groups", in honor of George Lusztig), and it is shown that they are exactly the "classical" Coxeter groups of finite and affine types A, B, C, and D. Thus, the combinatorial interpretations of descents, inversions, etc., carry over in these cases.^[42] Abacus models of minimum-length coset representatives for parabolic quotients have also been extended to this context.^[43]

Acknowledgements

The author thanks the three referees for their many helpful comments, and Max Glick for his help with the less technical summary. The work of the author was supported in part by a Simons Collaboration Grant (634530).

Notes

↑ Björner & Brenti (2005), p. 17.
↑ Humphreys (1990), p. 17.
↑ ^3.0 ^3.1 Humphreys (1990), Chapter 4.
↑ ^4.0 ^4.1 Humphreys (1990), Section 4.3.
↑ Björner & Brenti (2005), Chapter 8.3.
↑ Björner & Brenti (2005), Proposition 8.3.5.
↑ ^7.0 ^7.1 Chmutov, Pylyavskyy & Yudovina (2018), Section 1.6.
↑ Björner & Brenti (2005), p. 260.
↑ ^9.0 ^9.1 Björner & Brenti (2005), p. 15.
↑ Humphreys (1990), p. 93.
↑ Björner & Brenti (2005), p. 261.
↑ Björner & Brenti (2005), p. 208.
↑ Björner & Brenti (1996), Cor. 4.7.
↑ ^14.0 ^14.1 ^14.2 ^14.3 Björner & Brenti (2005), p. 263.
↑ Reiner (1995), p. 2.
↑ Petersen (2015), Chapter 14.
↑ Reiner (1995), Theorem 6.
↑ Lewis et al. (2019), Propositions 1.31 and 4.24.
↑ Lewis et al. (2019).
↑ Lewis et al. (2019), Theorem 4.25.
↑ Lewis et al. (2019), Corollary 2.5.
↑ Stembridge (1996), p. 353.
↑ Hanusa & Jones (2010), p. 1345.
↑ Crites (2010), Theorem 1.
↑ Hanusa & Jones (2010), Section 2.2.
↑ Lapointe & Morse (2005).
↑ Berg, Jones & Vazirani (2009).
↑ Björner & Brenti (2005), p. 264.
↑ Knutson, Lam & Speyer (2013), Section 2.1.
↑ As in (Cameron 1994, Section 3.5).
↑ As in, for example, (Beazley et al. 2015), (Lam 2015).
↑ ^32.0 ^32.1 Polster (2003), p. 42.
↑ Polster (2003), p. 22.
↑ Polster (2003), p. 15.
↑ Polster (2003), p. 43.
↑ Clark & Ehrenborg (2011), Theorem 2.2.
↑ Lewis (2020), Section 3.2.
↑ Kac (1990), Chapter 3.
↑ Kac (1990), Chapter 4.
↑ Kac (1990), Chapter 10.
↑ Kac (1990), Chapter 12.
↑ Björner & Brenti (2005), Chapter 8.
↑ Hanusa & Jones (2012).

↑ The three positions $i$ , $j$ , and $k$ need not lie in a single window. For example, the affine permutation $w$ in ${\widetilde {S}}_{4}$ with window notation $[-4,-1,1,14]$ is not fully commutative, because $w(0)=10$ , $w(3)=1$ , and $w(5)=0$ , even though no four consecutive positions contain a decreasing subsequence of length three.^[23]
↑ In a standard Young tableau, entries increase across rows and down columns; in a tabloid, they increase across rows, but there is no column condition.
↑ In other words, one might be interested in switching from a left group action to a right action or vice-versa.
↑ Not every sequence of $n$ nonnegative integers is a juggling sequence. In particular, a sequence corresponds to a "simple juggling pattern", with one ball caught and thrown at a time, if and only if the function $i\mapsto i+a_{i}\mod {n}$ is a permutation of $\{1,\ldots ,n\}$ .^[33]
↑ In some sources, unitary reflections are called pseudoreflections.

References

Beazley, Elizabeth; Nichols, Margaret; Park, Min Hae; Shi, XiaoLin; Youcis, Alexander (2015), "Bijective projections on parabolic quotients of affine Weyl groups", J. Algeb. Comb., 41: 911–948, doi:10.1007/s10801-014-0559-9
Berg, Chris; Jones, Brant; Vazirani, Monica (2009), "A bijection on core partitions and a parabolic quotient of the affine symmetric group", J. Combin. Theory Ser. A, 116 (8): 1344–1360, doi:10.1016/j.jcta.2009.03.013
Billey, Sara C.; Jockusch, William; Stanley, Richard P. (1993), "Some Combinatorial Properties of Schubert Polynomials", J. Algeb. Comb., 2: 345–374, doi:10.1023/A:1022419800503
Björner, Anders; Brenti, Francesco (1996), "Affine permutations of type A", Electron. J. Combin., 3 (2): R18, doi:10.37236/1276
Björner, Anders; Brenti, Francesco (2005), Combinatorics of Coxeter groups, Springer, doi:10.1007/3-540-27596-7, ISBN 978-3540-442387
Cameron, Peter J. (1994), Combinatorics: Topics, Techniques, Algorithms, Cambridge University Press, doi:10.1017/CBO9780511803888, ISBN 978-0-521-45761-3
Chmutov, Michael; Pylyavskyy, Pavlo; Yudovina, Elena (2018), "Matrix-ball construction of affine Robinson-Schensted correspondence", Selecta Math. (N.S.), 24 (2): 667–750, doi:10.1007/s00029-018-0402-6
Clark, Eric; Ehrenborg, Richard (2011), "Excedances of affine permutations", Advances in Applied Mathematics, 46: 175–191, doi:10.1016/j.aam.2009.12.006
Crites, Andrew (2010), "Enumerating pattern avoidance for affine permutations", Electron. J. Combin., 17 (1): R127, doi:10.37236/399
Ehrenborg, Richard; Readdy, Margaret (1996), "Juggling and applications to q-analogues", Discrete Math., 157: 107–125, doi:10.1016/S0012-365X(96)83010-X
Eriksson, Henrik; Eriksson, Kimmo (1998), "Affine Weyl groups as infinite permutations", Electron. J. Combin., 5: R18, doi:10.37236/1356
Green, R.M. (2002), "On 321-Avoiding Permutations in Affine Weyl Groups", J. Algeb. Comb., 15: 241–252, doi:10.1023/A:1015012524524
Hanusa, Christopher R.H.; Jones, Brant C. (2010), "The enumeration of fully commutative affine permutations", Eur. J. Comb., 31 (5): 1342–1359, doi:10.1016/j.ejc.2009.11.010
Hanusa, Christopher R.H.; Jones, Brant C. (2012), "Abacus models for parabolic quotients of affine Weyl groups", J. Algebra, 361: 134–162, doi:10.1016/j.jalgebra.2012.03.029
Humphreys, James E. (1990), Reflection groups and Coxeter groups, Cambridge University Press, doi:10.1017/CBO9780511623646, ISBN 0-521-37510-X
Kac, Victor G. (1990), Infinite dimensional Lie algebras (3rd ed.), Cambridge University Press, doi:10.1017/CBO9780511626234, ISBN 0-521-46693-8
Knutson, Allen; Lam, Thomas; Speyer, David E. (2013), "Positroid varieties: juggling and geometry", Compositio Math., 149: 1710–1752, doi:10.1112/S0010437X13007240
Lam, Thomas (2015), "The shape of a random affine Weyl group element and random core partitions", Ann. Probab., 43 (4): 1643–1662, doi:10.1214/14-AOP915
Lapointe, Luc; Morse, Jennifer (2005), "Tableaux on $k+1$ -cores, reduced words for affine permutations, and $k$ -Schur expansions", J. Combin. Theory Ser. A, 112 (1): 44–81, doi:10.1016/j.jcta.2005.01.003
Lewis, Joel Brewster (2020), "A note on the Hurwitz action on reflection factorizations of Coxeter elements in complex reflection groups", Electron. J. Combin., 27 (2): P2.54, doi:10.37236/9351
Lewis, Joel Brewster; McCammond, Jon; Petersen, T. Kyle; Schwer, Petra (2019), "Computing reflection length in an affine Coxeter group", Trans. Amer. Math. Soc., 371: 4097–4127, doi:10.1090/tran/7472
Petersen, T. Kyle (2015), Eulerian Numbers, Birkhauser, doi:10.1007/978-1-4939-3091-3, ISBN 978-1-4939-3090-6
Polster, Burkard (2003), The Mathematics of Juggling, Springer, doi:10.1007/b98883, ISBN 0-387-95513-5
Reiner, Victor (1995), "The distribution of descents and length in a Coxeter group", Electron. J. Combin., 2: R25, doi:10.37236/1219
Shephard, G. C.; Todd, J. A. (1954), "Finite unitary reflection groups", Canad. J. Math., 6: 274–304, doi:10.4153/CJM-1954-028-3
Shi, Jian-Yi (1986), Kazhdan–Lusztig cells of certain affine Weyl groups, Lecture Notes in Mathematics, vol. 1179, Springer, doi:10.1007/BFb0074968, ISBN 3-540-16439-1
Shi, Jian-Yi (1991), "The generalized Robinson–Schensted algorithm on the affine Weyl group of type $A n -1$ ", J. Algebra, 139 (2): 364–394, doi:10.1016/0021-8693(91)90300-W
Shi, Jian-Yi (2002), "Certain imprimitive reflection groups and their generic versions", Trans. Amer. Math. Soc., 354 (5): 2115–2129, doi:10.1090/S0002-9947-02-02941-0
Stembridge, John (1996), "On the Fully Commutative Elements of Coxeter Groups", J. Alg. Comb., 5: 353–385, doi:10.1007/BF00193185
Viennot, G. (1977), "Une forme géométrique de la correspondance de Robinson-Schensted", in Foata, Dominique (ed.), Combinatoire et représentation du groupe symétrique, Lecture Notes in Mathematics, vol. 579, Springer, pp. 29–58, doi:10.1007/BFb0090011, ISBN 978-3-540-08143-2

[Lewis-1] George Washington University

[2] wis@gwu.edu

[FOOTNOTEBjörnerBrenti200517-3] Björner & Brenti (2005), p. 17.

[FOOTNOTEHumphreys199017-4] Humphreys (1990), p. 17.

[FOOTNOTEHumphreys1990Chapter_4-5] 3.0 ^3.1 Humphreys (1990), Chapter 4.

[FOOTNOTEHumphreys1990Section_4.3-6] 4.0 ^4.1 Humphreys (1990), Section 4.3.

[FOOTNOTEBjörnerBrenti2005Chapter_8.3-7] Björner & Brenti (2005), Chapter 8.3.

[FOOTNOTEBjörnerBrenti2005Proposition_8.3.5-8] Björner & Brenti (2005), Proposition 8.3.5.

[FOOTNOTEChmutovPylyavskyyYudovina2018Section_1.6-9] 7.0 ^7.1 Chmutov, Pylyavskyy & Yudovina (2018), Section 1.6.

[FOOTNOTEBjörnerBrenti2005260-10] Björner & Brenti (2005), p. 260.

[FOOTNOTEBjörnerBrenti200515-11] 9.0 ^9.1 Björner & Brenti (2005), p. 15.

[FOOTNOTEHumphreys199093-12] Humphreys (1990), p. 93.

[FOOTNOTEBjörnerBrenti2005261-13] Björner & Brenti (2005), p. 261.

[FOOTNOTEBjörnerBrenti2005208-14] Björner & Brenti (2005), p. 208.

[FOOTNOTEBjörnerBrenti1996Cor._4.7-15] Björner & Brenti (1996), Cor. 4.7.

[FOOTNOTEBjörnerBrenti2005263-16] 14.0 ^14.1 ^14.2 ^14.3 Björner & Brenti (2005), p. 263.

[FOOTNOTEReiner19952-17] Reiner (1995), p. 2.

[FOOTNOTEPetersen2015Chapter_14-18] Petersen (2015), Chapter 14.

[FOOTNOTEReiner1995Theorem_6-19] Reiner (1995), Theorem 6.

[FOOTNOTELewisMcCammondPetersenSchwer2019Propositions_1.31_and_4.24-20] Lewis et al. (2019), Propositions 1.31 and 4.24.

[FOOTNOTELewisMcCammondPetersenSchwer2019-21] Lewis et al. (2019).

[FOOTNOTELewisMcCammondPetersenSchwer2019Theorem_4.25-22] Lewis et al. (2019), Theorem 4.25.

[FOOTNOTELewisMcCammondPetersenSchwer2019Corollary_2.5-23] Lewis et al. (2019), Corollary 2.5.

[FOOTNOTEStembridge1996353-24] Stembridge (1996), p. 353.

[FOOTNOTEHanusaJones20101345-25] Hanusa & Jones (2010), p. 1345.

[FOOTNOTECrites2010Theorem_1-27] Crites (2010), Theorem 1.

[FOOTNOTEHanusaJones2010Section_2.2-28] Hanusa & Jones (2010), Section 2.2.

[FOOTNOTELapointeMorse2005-29] Lapointe & Morse (2005).

[FOOTNOTEBergJonesVazirani2009-30] Berg, Jones & Vazirani (2009).

[FOOTNOTEBjörnerBrenti2005264-31] Björner & Brenti (2005), p. 264.

[FOOTNOTEKnutsonLamSpeyer2013Section_2.1-34] Knutson, Lam & Speyer (2013), Section 2.1.

[35] As in (Cameron 1994, Section 3.5).

[36] As in, for example, (Beazley et al. 2015), (Lam 2015).

[FOOTNOTEPolster200342-37] 32.0 ^32.1 Polster (2003), p. 42.

[FOOTNOTEPolster200322-38] Polster (2003), p. 22.

[FOOTNOTEPolster200315-40] Polster (2003), p. 15.

[FOOTNOTEPolster200343-41] Polster (2003), p. 43.

[FOOTNOTEClarkEhrenborg2011Theorem_2.2-42] Clark & Ehrenborg (2011), Theorem 2.2.

[FOOTNOTELewis2020Section_3.2-44] Lewis (2020), Section 3.2.

[FOOTNOTEKac1990Chapter_3-45] Kac (1990), Chapter 3.

[FOOTNOTEKac1990Chapter_4-46] Kac (1990), Chapter 4.

[FOOTNOTEKac1990Chapter_10-47] Kac (1990), Chapter 10.

[FOOTNOTEKac1990Chapter_12-48] Kac (1990), Chapter 12.

[FOOTNOTEBjörnerBrenti2005Chapter_8-49] Björner & Brenti (2005), Chapter 8.

[FOOTNOTEHanusaJones2012-50] Hanusa & Jones (2012).

[26] The three positions $i$ , $j$ , and $k$ need not lie in a single window. For example, the affine permutation $w$ in ${\widetilde {S}}_{4}$ with window notation $[-4,-1,1,14]$ is not fully commutative, because $w(0)=10$ , $w(3)=1$ , and $w(5)=0$ , even though no four consecutive positions contain a decreasing subsequence of length three.^[23]

[32] In a standard Young tableau, entries increase across rows and down columns; in a tabloid, they increase across rows, but there is no column condition.

[33] In other words, one might be interested in switching from a left group action to a right action or vice-versa.

[39] Not every sequence of $n$ nonnegative integers is a juggling sequence. In particular, a sequence corresponds to a "simple juggling pattern", with one ball caught and thrown at a time, if and only if the function $i\mapsto i+a_{i}\mod {n}$ is a permutation of $\{1,\ldots ,n\}$ .^[33]

[43] In some sources, unitary reflections are called pseudoreflections.

[a]

[i]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[a]

[24]

[25]

[26]

[27]

[28]

[b]

[c]

[29]

[30]

[31]

[32]

[d]

[34]

[35]

[36]

[e]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[23]

[33]