Numeral systems
Main Course Launch Page - Data Size and Speeds
Exit Supplmental Material
Supplemental Course Navigation
| << Previous - Hardware | Next - Data sizes and speeds >> |
|---|
This is a lesson in in the course Introduction to Computers, which is a part of The School of Computer Science
| Subject classification: this is an information technology resource. |
| Educational level: this is a secondary education resource. |
| Type classification: this is a lesson resource. |
| Completion status: this resource is ~75% complete. |
Objective
[edit | edit source]Familiarize the learner with method for expressing numbers and convert one method to another.
Introduction
[edit | edit source]A writing method for expressing numbers is called a "numeral system". In the most common numeral system, we write numbers with combinations of 10 symbols {0,1,2,3,4,5,6,7,8,9}. These symbols are called digits, and numbers that are expressed using 10 digits are called "decimal" or "base-10" numbers. The other most common numeral systems are binary, hexadecimal and octal. The binary numeral system, or base-2 number system, represents numeric values using two symbols: 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used internally by almost all modern computers.
Decimal Numeral System
[edit | edit source]In the first method discussed we write numbers with combinations of 10 symbols {0,1,2,3,4,5,6,7,8,9} called digits. Numbers that are expressed with 10 digits are called "base-10" numbers or "Decimal Numeral System". For example:
2 (one digit)
45 (two digit)
643 (three digit)
8785 (four digit)
etc.
In Decimal Numeral Systems, the value of a digit is multiplied according to its placement in a numerical sequence: (base-number ^ 0,1,2,3,...), from right to left.

First digit = (base-number ^ 0): 10^0 = 1
Second digit =(base-number ^ 1): 10^1 = 10
Third digit =(base-number ^ 2): 10^2 = 100
Fourth digit =(base-number ^ 3): 10^3 = 1000
etc.
For example:
20= (2*10)+(0*1)=20+0=20
456=(4*100)+(5*10)+(6*1)=400+50+6
84568=(8*10000)+(4*1000)+(5*100)+(6*10)+(8*1)=80000+4000+500+60+8
Binary Numeral System
[edit | edit source]Numbers expressed with 2 symbols (0, 1) are called binary, or "base-2" numbers.
For example:
1 (one-digit-read: 1)
10 (two-digit-read: 1, 0)
100 (three-digit-read: 1,0,0)
1101 (four-digit-read: 1, 1, 0, 1)
etc.
In the Binary Numeral System, digits have a value specified, this value being equal with (base-number ^ 0,1,2,3,...): (right to left)

First digit (base-number^0): 2^0 = 1
Second digit (base-number^1): 2^1 = 2
Third digit (base-number^2): 2^2 = 4
Fourth digit (base-number^3): 2^3 = 8
etc.
Converting Binary to Decimal
[edit | edit source]To convert binary to decimal, each digit is multiplied by the value of its position, and the results are added.
For example:
10 = (1*2^1) + (0*2^0) = 1*2 + 0*1 = 2 + 0 = 2 → 10 (binary) =2 (decimal)
101 = (1*2^2) + (0*2^1) + (1*2^0) = 1*4 + 0*2 + 1*1 = 4 + 0 + 1 = 5 → 101 (binary) =5 (decimal )
11001 = (1*2^4) + (1*2^3) + (0*2^2) + (0*2^1) + (1*2^0) = 1*16 + 1*8 + 0*4 + 0*2 + 1*1 = 16 + 8 + 0 + 0 + 1 = 25 → 11001 (binary) =25 (decimal)
111011 = (1*2^5) + (1*2^4) + (1*2^3) + (0*2^2) + (1*2^1) + (1*2^0) = 1*32 + 1*16 + 1*8 + 0*4 + 1*2 + 1*1 = 32 + 16 + 8 + 0 + 2 + 1 = 59 → 111011 (binary) =59 (decimal)
Converting Decimal to Binary
[edit | edit source]To convert decimal to binary
Divide the decimal number by 2
- If there IS a remainder the rightmost column will be a 1
- If there is NO remainder, the rightmost column will be a 0.
Then repeat the process, moving one column to the left each time until you have divided down to 1.
Example 1
15/2 = 7 remainder 1 (Binary number = ???1)
7/2 = 3 remainder 1 (Binary number = ??11)
3/2 = 1 remainder 1 (Binary number = ?111)
The final result will always be 1 in the leftmost column (Binary number = 1111)
Example 2
74/2 = 37 remainder 0 (Binary number = ??????0)
37/2 = 18 remainder 1 (Binary number = ?????10)
18/2 = 9 remainder 0 (Binary number = ????010)
9/2 = 4 remainder 1 (Binary number = ???1010)
4/2 = 2 remainder 0 (Binary number = ??01010)
2/2 = 1 remainder 0 (Binary number = ?001010)
The final result will always be 1 in the leftmost column (Binary number = 1001010)
NB - Although I've put ? in at each stage, you won't know how many columns are needed until you complete the process.
For a shortcut to see how many columns are needed, find the largest factor of 2 that is smaller than the decimal number you started with, e.g.
Example 1: The largest factor less than 74 is 64, which is 2 to the power 6. As the furthest right column is 2 to the power 0, this means we need 7 columns.

Hexadecimal Numeral System
[edit | edit source]Numbers written with 16 symbols {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} are called "base-16" numbers. For example:
A (one digit)
B5 (two digit)
6C3 (three digit)
AF85 (four digit)
etc.
so:
A(hexadecimal)=10(decimal).
B(hexadecimal)=11(decimal).
C(hexadecimal)=12(decimal).
D(hexadecimal)=13(decimal).
E(hexadecimal)=14(decimal).
F(hexadecimal)=15(decimal)
In the "Hexadecimal Numeral System", digits have a value specified, this value of digits is equal with (base-number^ 0,1,2,3,...):(right to left)

First digit (base-number ^ 0): 16^0 = 1
Second digit (base-number ^ 1): 16^1 = 16
Third digit (base-number ^ 2): 16^2 = 256
fourth digit (base-number ^ 3): 16^3 = 4096
etc.
Converting Hexadecimal to Decimal
[edit | edit source]To convert hexadecimal to decimal, each digit is multiplied by the value of its position, and the results are added.
For example:
A = (10*16^0) = 10*1 = 10 → A(hexadecimal) =10(decimal)
B5 = (11*16^1) + (5*16^0) = 11*16 + 5*1 = 181 → B5(hexadecimal) =181(decimal)
6C3 = (6*16^2) + (12*16^1) + (3*16^0) = 6*256 + 12*16 + 3*1 = 1536 + 192 + 3 = 1731 → 6C3(hexadecimal) =1731(decimal)
AF85 = (10*16^3) + (15*16^2) + (8*16^1) + (5*16^0) = 10*4096 + 15*256 + 8*16 + 5*1 = 40960 + 3840 + 128 + 5 = 44933 → AF85(hexadecimal) =44933(decimal)
Converting Decimal to Hexadecimal
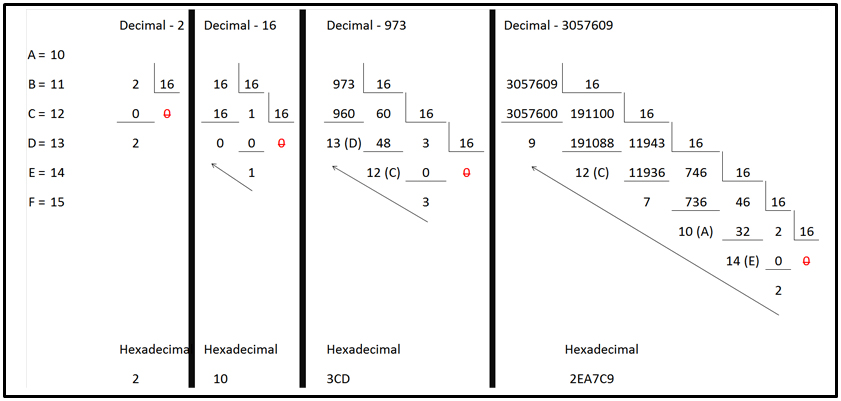
[edit | edit source]To convert decimal to hexadecimal
• Divide the decimal number by 16 - the remainder given is the last hexadecimal value.
• The quotient is then divided by 16 to get another remainder. Like the binary calculation the values are read right to left (first remainder value is the last in the hexadecimal number, then next to last, third to last, etc.)
• The process is terminated once a dividend (numerator) of less than 16 is reached. Continuing to divide by 16 would give a quotient of 0 which is indivisible.
• Keep in mind that 10-15 are represented as single character "numbers" in the hexadecimal system. A=10 , B=11 , C = 12 , D = 13 , E= 14 , F =15 - remainders must reflect their appropriate hexadecimal value.
Examples
• Decimal 15
- o 15/16 remainder is 15 (>16 so process terminates) so the "number" value is F
• Decimal 16
- o 16/16 remainder is 0 [hex ?0]
- o The quotient of 1 is then divided - 1/16 which leaves a remainder of 1 (giving a quotient of 0 so process terminates) [hex 10]
• Decimal 45
- o 45/16 – remainder 13 [hex ?D]
- o Quotient 2 | 2/16 – remainder 2 [hex 2D]
• Decimal 47825
- o 47825/16 - remainder 1 [hex ???1]
- o Quotient 2989 | 2989/16 – remainder 13 [hex ??D1]
- o Quotient 186 | 186/16 – remainder 10 [hex ?AD1]
- o Quotient 11 | 11/16 – remainder 11 [hex BAD1]
References
[edit | edit source]Supplemental Course Navigation
| << Previous - Hardware | Next - Data sizes and speeds >> |
|---|
