Complex Analysis/Paths
Definition: Path
[edit | edit source]Let be a subset. A path in is a continuous mapping with:
- with and .
Definition: Trace of a Path
[edit | edit source]The trace of a path in is the image or range of the function :
Definition: Closed Path
[edit | edit source]Let be a path in . The mapping is called a closed path if:
Definition: Region
[edit | edit source]Let be an open subset of . Then is called a region.
Definition: Path-Connected
[edit | edit source]Let be a non-empty set.
- is path-connected
Definition: Domain
[edit | edit source]Let be a non-empty subset of . If
- is open
- is path-connected
Then is called a domain in .
Example (Circular Paths)
[edit | edit source]Let be a complex number, and let be a radius. A circular path around is defined as:
Example - Paths with Ellipse as Trace
[edit | edit source]Let be a complex number, and let be the semi-axes of an ellipse. An elliptical path around is defined as:
Gardener's Construction of an Ellipse
[edit | edit source]Convex Combinations
[edit | edit source]Let be complex numbers, and let be a scalar. A path is defined such that its trace is the line segment connecting :
Such a path is called a convex combination of the first order (see also Convex Combinations of higher order).
Animation of a Convex Combination of Two Vectors as Mapping
[edit | edit source]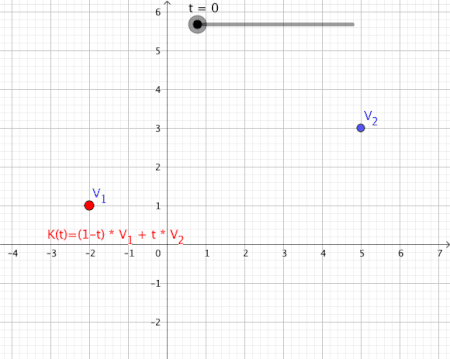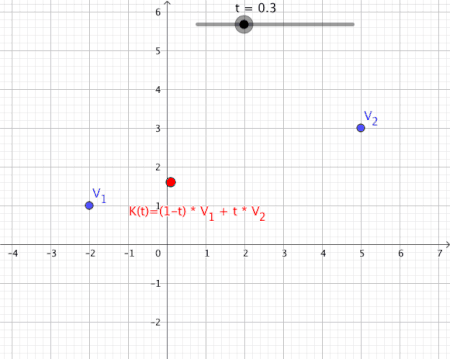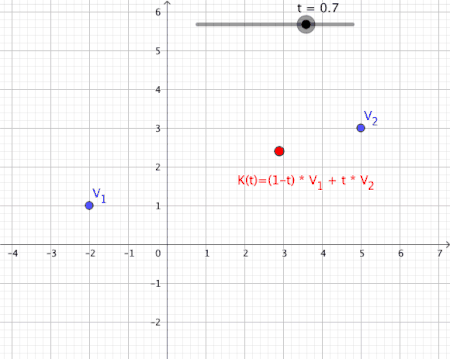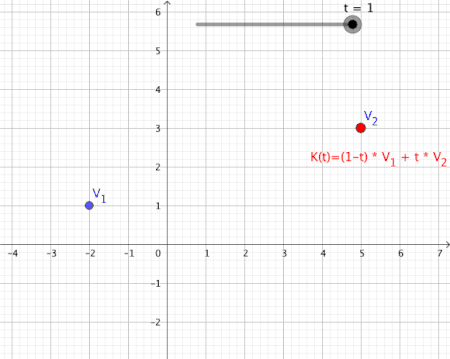
Integration Path
[edit | edit source]Let be a domain. An integration path in is a path that is piecewise continuously differentiable with
- with and .
Remark
[edit | edit source]An integration path can, for example, be expressed piecewise as convex combinations between multiple points . The overall path does not need to be differentiable at points . The trace of such a path is also called a polygonal path.
See Also
[edit | edit source]Page Information
[edit | edit source]You can display this page as Wiki2Reveal slides
Wiki2Reveal
[edit | edit source]TheWiki2Reveal slides were created for the Complex Analysis' and the Link for the Wiki2Reveal Slides was created with the link generator.
- This page is designed as a PanDocElectron-SLIDE document type.
Translation and Version Control
[edit | edit source]This page was translated based on the following [https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Wege Wikiversity source page] and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:
- Source: Kurs:Funktionentheorie/Wege - URL:
https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Wege
- Date: 12/17/2024



![{\displaystyle \gamma \colon [a,b]\rightarrow U}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e64ae78f386a9c5e428536d26cbc1d52f9bd7082)



![{\displaystyle \mathrm {Trace} (\gamma ):={\gamma (t)\in \mathbb {C} \ |\ t\in [a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bbf148e5246a00fb4a1f35736ceb05ab2e6e800)


![{\displaystyle :\Longleftrightarrow \ \forall _{z_{1},z_{2}\in U}\exists _{\gamma \colon [a,b]\rightarrow U}:\ \gamma (a)=z_{1}\wedge \gamma (b)=z_{2}\wedge {Spur}(\gamma )\subseteq U}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9ef5a020e80a216f7b9177227cebd745a2c87e7)




![{\displaystyle \gamma _{z_{o},r}\colon [0,2\pi ]\rightarrow \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ea69dae2350897859f84f440a9916973f02adb5)


![{\displaystyle \gamma _{z_{o},a,b}\colon [0,2\pi ]\rightarrow \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4f36d881b6f2e490ed3696eea651cdbe5f8d1b4)



![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)
![{\displaystyle \gamma _{z_{1},z_{2}}\colon [0,1]\rightarrow \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d17989c4d0e56a79611d406f2a685114de84641)

