Convex Combination

Visualization of a convex combination of degree 1., 2. and 3. in Geogebra 

Introduction

Let $(V,+,\cdot ,\mathbb {R} )$ be a real vector space. A Linear combination is called a convex combination if all coefficients $\lambda _{i}\in [0,1]$ are from the unit interval [0,1] and the sum of all $\lambda _{i}$ for the vectors $v_{i}\in V$ with $i\in \{1,\ldots ,n\}$ equals 1:

${\begin{array}{rcl}v&=&\lambda _{1}v_{1}+\lambda _{2}v_{2}+\dotsb +\lambda _{n}v_{n}\\&=&\sum _{i=1}^{n}\lambda _{i}v_{i},\\&{\mbox{with}}&0\leq \lambda _{i}\leq 1,\quad \sum _{i=1}^{n}\lambda _{i}=1\,.\end{array}}$

Convex combinations in the plane

When considering convex combinations in the plane, the underlying vector space is the two-dimensional space $V:=\mathbb {R} ^{2}$. First, we consider convex combinations of two vectors in $\mathbb {R} ^{2}$. By the condition $\lambda _{1}+\lambda _{2}=1$, both scalars are dependent on each other. If $tis\in [0,1]$, then set $\lambda _{1}:=(1-t)$ and $\lambda _{2}:=t$, for example.

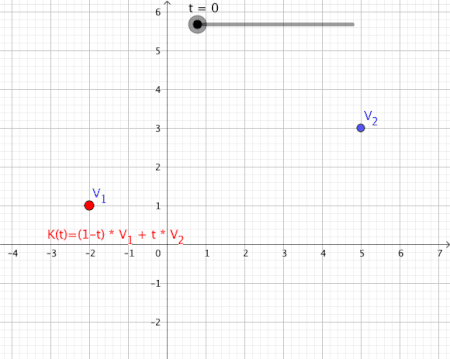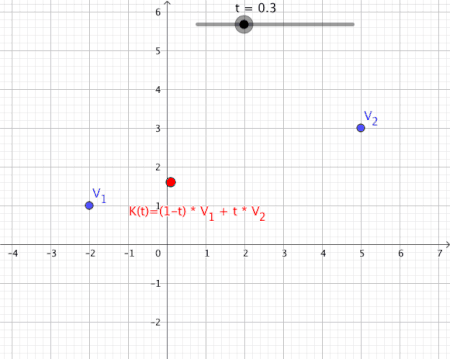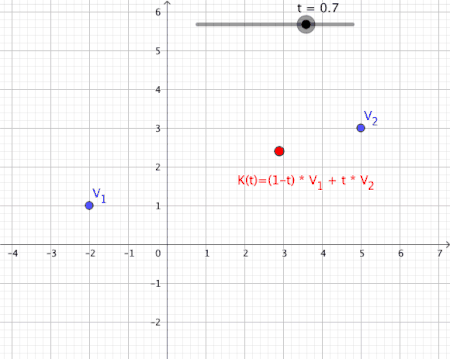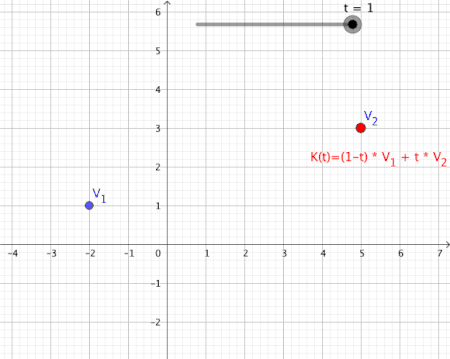
Convex combinations as mappings into vector space

Considering now a mapping $K\colon [0,1]\to V$, we can generally represent 1st order convex combinations of 2 vectors $v_{1},v_{2}\in V$ as follows over the mapping $K$:

$K(t):=(1-t)\cdot v_{1}+t\cdot v_{2}$

Animation of a convex combination of two vectors as a figure

Convex combinations of 2 vectors in function spaces

Treating convex combination with $v_{1},v_{2}\in \mathbb {R} ^{2}$ or $v_{1},v_{2}\in \mathbb {R} ^{3}$ provides an illustration in secondary school vector spaces as special linear combinations. However, convex combinations can also be applied to function spaces. For example, let $f,g\in V:={\mathcal {C}}([a,b],\mathbb {R} )$, then $\lambda _{1},\lambda _{2}\in [0,1]$ and $\lambda _{1}+\lambda _{2}=1$ give rise to a new function $h_{t}\in V$ with:

$h_{t}:=(1-t)\cdot f+t\cdot g$

The subscript $t$ in $h_{t}$ is used because a different function $h_{t}$ is defined as a function of $t$.

Example of convex combinations of functions

Let $[a,b]=[4,7]$ and as the first function $f:[a,b]\to \mathbb {R}$ a polynomial is defined.

$f(x):={\frac {3}{10}}\cdot x^{2}-2$

A trigonometric function $g:[a,b]\to \mathbb {R}$ is chosen as the second function.

$g(x):=2\cdot cos(x)+1$

The following figure illustrates the convex combination $K(t):=(1-t)\cdot f+t\cdot g$.

Animation for convex combinations of functions

The following animation shows several convex combinations of two given functions.

Geogebra: Interactive Applet - Download:' Geogebra-File

Remark - Deformation

If the first function $f$ describes the initial shape and $g$ describes the target shape, convex combinations can be described, for example, in computer graphics for the deformation of an initial shape into a target shape.

Convex combinations of convex combinations

In the animation above you can see a convex combination of 2 vectors viewed in the plane or in a function space. If one uses three points then one can create a 1st order convex combination between every two points. We will now consider higher order convex combinations by constructing, for example, a 2nd order convex combination from two 1st order convex combinations. Generally from 2 convex combinations of order $n$ one convex combination of order $n+1$ can be formed.

Convex hull

The set of all convex combinations of a given set of vectors is called a convex hull (see also p-convex hull).

Video convex combinations in the plane

Geogebra: Interactive applet - Download:' Geogebra-File

Remarks Video about convex combinations of order 1, 2 and 3 in Geogebra

In the video you can see convex combinations of the

• 1st order between $A_{1}$ and $B_{1}$ without auxiliary points,
• 2nd order between $A_{2}$ and $B_{2}$ with auxiliary point $S_{1}$,
• 3rd order between $A_{3}$ and $B_{3}$ with auxiliary points $H_{1},H_{2}$,

Convex combinations as polynomials of t

Convex combinations can be conceived as polynomials where the coefficients come from a vector space $(V,+,\cdot ,\mathbb {R} )$ (see also Polynomial Algebra). For example, if one chooses $V:=\mathbb {R} ^{n}$, one can take a convex combination $K$ to be an element of Polynomial Algebra $V[t]$.

3D convex combination - 1st order

For example, choosing $n=3$ and $V:=\mathbb {R} ^{3}$, a 1st order convex combination is defined as follows.

$A={\begin{pmatrix}1\\2\\4\end{pmatrix}},\,B={\begin{pmatrix}4\\1\\0\end{pmatrix}},\,\,K(t):=(1-t)\cdot A+t\cdot B=(B-A)\cdot t+A$

Thus, a 1st order convex combination yields a polynomial of degree 1. with argument $t$. Represent the convex combination in Geogebra 3D with $t\in [0,1]$ (see also Representation of a Straight Line by Direction Vector and Location Vector).

3D convex combination - 2nd order

Choosing again $n=3$ and $V:=\mathbb {R} ^{3}$ with an auxiliary point $H_{1}\in V$, two 1st order convex combinations yield 2nd order convex combinations.

$H_{1}={\begin{pmatrix}2\\2\\2\end{pmatrix}},{\begin{array}{rcl}K_{(1,1)}(t)&:=&(H_{1}-A)\cdot t+A\\K_{(1,2)}(t)&:=&(B-H_{1})\cdot t+H_{1}\\K_{2}(t)&:=&((H_{1}-A)\cdot t+A)\cdot (1-t)+((B-H_{1})\cdot t+H_{1})\cdot t\end{array}}$

Represent $K_{2}$ as a polynomial $K_{2}(t)=P_{2}\cdot t^{2}+P_{1}\cdot t^{1}+P_{0}\cdot t^{0}$ and calculate for $n=2$ ($n=3,4,...$) the coefficients in $P_{k}\in V=\mathbb {R} ^{3}$.

Bernstein polynomial - order 1

${\begin{array}{rcl}K_{1}(t)&:=&A\cdot (1-t)+B\cdot t\\&=&A\cdot (1-t)^{1}\cdot t^{0}+B\cdot (1-t)^{0}\cdot t^{1}\\\end{array}}$

Calculation of the polynomial - order 2

${\begin{array}{rcl}K_{2}(t)&:=&((H_{1}-A)\cdot t+A)\cdot (1-t)+((B-H_{1})\cdot t+H_{1})\cdot t\\&=&(H_{1}\cdot t-A\cdot t+A)-(H_{1}\cdot t^{2}-A\cdot t^{2}+A\cdot t)\\&&+(B\cdot t^{2}-H_{1}\cdot t^{2}+H_{1}\cdot t)\\&=&(B-H_{1}+A)\cdot t^{2}+2\cdot (H_{1}-A)\cdot t+A\end{array}}$

Bernstein polynomial - order 2

${\begin{array}{rcl}K_{2}(t)&:=&((H_{1}-A)\cdot t+A)\cdot (1-t)+((B-H_{1})\cdot t+H_{1})\cdot t\\&=&A\cdot (1-t)^{2}+2\cdot H_{1}\cdot t\cdot (1-t)+B\cdot t^{2}\end{array}}$

Bernstein polynomial - order 3

${\begin{array}{rcl}K_{3}(t)&:=&A\cdot (1-t)^{3}+3\cdot H_{1}\cdot (1-t)^{2}\cdot t+3\cdot H_{2}\cdot (1-t)\cdot t^{2}+B\cdot t^{3}\end{array}}$

Task: calculation of the polynomial - order 3

• Calculate the polynomial of degree 3 and derive from it the general formula for the coefficients of $t^{n}$. To do this, use the notation $H_{0}:=A$ and $H_{n}:=B$ for convex combinations of order $n$ between points $A$ and $B$ with auxiliary points $H_{1},\ldots ,H_{n-1}$.
• Prove your conjecture by complete induction.

$K_{n}(t):=\sum _{k=0}^{n}{n \choose k}\cdot H_{k}\cdot t^{k}\cdot (1-t)^{n-k}$

Interactive geogebra worksheet

The video shows an interaction with the convex combinations above. From Geogebra, the worksheet created was uploaded to the Geogebra materials page. You can use this directly in your browser at the following link:

Interactive Worksheet: Convex Combination on Geogebra

Convex combination as a figure

A convex combination can be used to interpolate points $A=v_{1}$ and $B=v_{n}$. Furthermore, if the auxiliary points $H_{1}=v_{2}$,....$H_{n_{1}}=v_{n-1}$ are given for a convex combination $n$-th order. The convex combinations can be generally thought of as mapping from the interval $[0,1]$ to $\mathbb {R} ^{n}$ as follows:

${\begin{array}{rcl}K_{n}:&[0,1]&\rightarrow &\mathbb {R} ^{n}\\&t&\mapsto &\displaystyle \sum _{k=0}^{n}(1-t)^{n-k}\cdot t^{k}\cdot v_{k+1}\\&&&=(1-t)^{n}v_{1}+(1-t)^{n-1}tv_{2}+\ldots +t^{n}v_{n}\end{array}}$

Convex Combinations in Geogebra - Download

In Geogebra, you can dynamically visualize the geometric meaning of convex combinations. At the

• GitHub repository you can download.
• Download sample files of convex combinations for Geogebra as a ZIP file.
• The GitHub repository further contains a wxMaxima file for the algebraic calculation of the points lying on the convex combination. Data points from the $\mathbb {R} ^{3}$ are also included there, showing that the entire construction of the convex combination can also be applied to the $\mathbb {R} ^{3}$ or the $\mathbb {R} ^{n}$.

In the example files convex combinations of two points (vectors $v_{1},v_{2}\in \mathbb {R} ^{2}$) are treated.

Definition of convex combinations as mappings/curves in vector space

1st order convex combination

• 1st order convex combination generate all points on the connecting line between the two points $v_{1},v_{2}\in \mathbb {R} ^{2}$.

$K_{1}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot v_{1}+\lambda \cdot v_{2}$.

2nd order convex combination

• A 2nd order convex combination arises with another auxiliary points $h_{1}\in \mathbb {R} ^{2}$ in the plane from the following two 1st order convex combinations:

$K_{1,1}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot v_{1}+\lambda \cdot h_{1}$ (1st order convex combination between $v_{1},h_{1}\in \mathbb {R} ^{2}$)

$K_{1,2}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot h_{1}+\lambda \cdot v_{2}$ (1st order convex combination between $h_{1},v_{2}\in \mathbb {R} ^{2}$)

$K_{2}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot K_{1,1}(\lambda )+\lambda \cdot K_{1,2}(\lambda )$ (2nd order convex combination. Order between $v_{1},v_{2}\in \mathbb {R} ^{2}$ with auxiliary point $h_{1}\in \mathbb {R} ^{2}$)

3rd order convex combination

A 3rd order convex combination arises with two more auxiliary points $h_{1},h_{2}\in \mathbb {R} ^{2}$ in the plane from the following three 1st order convex combinations:

$K_{1,1}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot v_{1}+\lambda \cdot h_{1}$ (1st order convex combination between $v_{1},h_{1}\in \mathbb {R} ^{2}$)

$K_{1,2}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot h_{1}+\lambda \cdot h_{2}$ (1st order convex combination between $h_{1},h_{2}\in \mathbb {R} ^{2}$)

$K_{1,3}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot h_{2}+\lambda \cdot v_{2}$ (1st order convex combination between $h_{2},v_{2}\in \mathbb {R} ^{2}$)

2nd order convex combinations from 1st order KK

From the three 1st order convex combinations, construct two 2nd order convex combinations as follows:

$K_{2,1}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot K_{1,1}(\lambda )+\lambda \cdot K_{1,2}(\lambda )$ (2nd order convex combination. Order between $v_{1},h_{2}\in \mathbb {R} ^{2}$ with auxiliary point $h_{1}\in \mathbb {R} ^{2}$)

$K_{2,2}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot K_{1,2}(\lambda )+\lambda \cdot K_{1,3}(\lambda )$ (2nd order convex combination. Order between $h_{1},v_{2}\in \mathbb {R} ^{2}$ with auxiliary point $h_{2}\in \mathbb {R} ^{2}$)

3rd order convex combinations from 2nd order KK

From the two 2nd order convex combinations, a 3rd order convex combination is now obtained as follows:

$K_{3}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot K_{2,1}(\lambda )+\lambda \cdot K_{2,2}(\lambda )$ (2nd order convex combination. Order between $v_{1},v_{2}\in \mathbb {R} ^{2}$ with auxiliary points $h_{1},h_{2}\in \mathbb {R} ^{2}$)

Convex combinations of n-th order

In general, a convex combination of $n$-th order has.

• $n-1$ auxiliary points $h_{1},\ldots ,h_{n_{1}}$
• $n$ 1st order convex combinations,
• $n-1$ 2nd order convex combinations,
• ...
• $n-k$ convex combinations $(k+1)$-th order,
• ...
• $1$ convex combination n-th order,

In 3D graphics, 3rd-order convex combinations are particularly important (see Bezier curves).

Convex combination of functions

Let $\mathbb {D}$ be a domain of definition of functions and $(V,+,\cdot ,\mathbb {K} )$ be a vector space over the body $\mathbb {K}$ (e.g. $\mathbb {K} :=\mathbb {R} ,\mathbb {C}$ and ${\mathcal {C}}(\mathbb {D} ,V)$ the set of continuous functions from $\mathbb {D}$ to $V$. A convex combination of two continuous functions $f,g\in {\mathcal {C}}(\mathbb {D} ,V)$ with $\lambda \in [0,1]\subset \mathbb {K}$ is defined by:

$h_{\lambda }:=(1-\lambda )\cdot f+\lambda \cdot g$

Where

${\begin{array}{rcl}h_{\lambda }:\mathbb {D} &\to &V\\z&\mapsto &h_{\lambda }(z):=(1-\lambda )\cdot f(z)+\lambda \cdot g(z)\\\end{array}}$

Convex combinations of more than 2 vectors

In the above case, two vectors from the underlying vector space were studied as convex combinations and higher order convex combinations were also constructed. Now the procedure is extended to more than 2 vectors, again using a parametrization over vectors $(t_{1},\ldots ,t_{n})\in [0,1]^{n}$.

Convex combinations of 3 vectors

Extend the approach to convex combination with two parameters $t_{1},t_{2}\in [0,1]$ and vectors $v_{1},v_{2},v_{2}$ via:

$\lambda _{1}:=(1-t_{1}),\,\lambda _{2}:=t_{1}\cdot (1-t_{2}),\,\lambda _{3}:=t_{1}\cdot t_{2}$

and the mapping for the convex combinations into the closed triangle defined by the three vectors $v_{1},v_{2},v_{2}$:

$K_{3}(t_{1},t_{2}):=\underbrace {(1-t_{1})} _{=\lambda _{1}}\cdot v_{1}+\underbrace {t_{1}\cdot (1-t_{2})} _{=\lambda _{2}}\cdot v_{2}+\underbrace {t_{1}\cdot t_{2}} _{=\lambda _{3}}\cdot v_{3}$

Convex combinations of 4 vectors

For 4 vectors, again use as parameterization $(t_{1},t_{2})\in [0,1]\times [0,1]$

$\lambda _{1}:=(1-t_{1})\cdot (1-t_{2}),\,\lambda _{2}:=t_{1}\cdot (1-t_{2}),$

$\lambda _{3}:=(1-t_{1})\cdot t_{2},\,\lambda _{4}:=t_{1}\cdot t_{2}$

The mapping $K_{4}:[0,1]^{2}\to V$ then represents all vectors from the convex hull of $v_{1},v_{2},v_{3},v_{4}\in V$.

$K_{4}(t_{1},t_{2}):=\underbrace {(1-t_{1})(1-t_{2})} _{=\lambda _{1}}\cdot v_{1}+\underbrace {t_{1}(1-t_{2})} _{=\lambda _{2}}\cdot v_{2}+\underbrace {(1-t_{1})t_{2}} _{=\lambda _{2}}\cdot v_{3}+\underbrace {t_{1}\cdot t_{2}} _{=\lambda _{4}}\cdot v_{3}$

Task

• (Geogebra) Analyze the Geogebra sample files and describe the importance of the auxiliary points for the shape of the locus line in the Dynamic Geometry Software (DGS) Geogebra.
• What role do the auxiliary points play in creating differentiable interpolations (tangent vectors).
• (Interpolation) Compare Lagrange or Newton interpolations for many data points with interpolation by several 3rd order convex combinations. What are the strengths and weaknesses (oscillation between data points) of the different methods. Veranschaulichen Sie diese mit Geogebra.

Task - 3. Order and functional representatio

• (Convexcombination 3-rd Order) Calculate the points convexcombinationen 3 Order in $\mathbb {R} ^{3}$ with Maxima CAS (see also Maxima Tutorial der FH-Hagen).

K(t):= A * (1-t)^3 + H1 * (1-t)^2 * t + H2 * (1-t) * t^2 + B * t^3

Defination the poits as 3x1-Matrices with:

A : matrix( [-1], [3], [-4] )

• (Differece between Convexcombination 3rd Order and cubic Splines)Analyze the similarities and differences between cubic splines and third-order convex combinations! What is the application context of cubic splines? When would you use convex combinations?

Learning Task - Convex combination of Functions

• (Convex combination of Functions) Choose $\mathbb {D} :=\mathbb {R}$ $V:=\mathbb {R}$ and represent the convex combination of $f$ and $g$ in Geogebra with a slider $\lambda$ (analogous to the GIF animation), where $f(x)=x^{2}$ and $g(x)=cos(x)$. What do you observe when you move the slider from 0 to 1? $g(x)=cos(x)$ is bounded and $f(x)=x^{2}$ is unbounded on $\mathbb {D} :=\mathbb {R}$. What is the property of $h_{\lambda }$ for $0<\lambda <1$?
• (Convex combinations and polynomialgebras) Summarize the convex combination of order $n$ with coefficients from a vector space by powers of $t^{n}$ and consider the coefficients from the vector space $V$ in general. How are the coefficients of the polynomials formed from the points or auxiliary points for the powers? (See also Polynomial algebra and Bezier curves).

Learning Task - Bernstein polynomials and de-Casteljau algorithm

• (Bernstein polynomials) Analyze the connection of convex combinations as special linear combinations from linear algebra with Bernstein polynomials and Bezier curves. Bernstein polynomials for a certain degree $n\in \mathbb {N}$ represent a decomposition of one. Which relation exists concerning a decomposition of one for convex combinations. What is the meaning of a polynomial representation with respect to a decomposition of one?

$\lambda _{1}+\ldots +\lambda _{n}=\sum _{k=1}^{n}\lambda _{k}=1$

• (De Casteljau's algorithm) Analyze the De Casteljau's algorithm and explain the role of the Bernstein polynomials as control polynomials for the defining points of the curve.

Interpolations

Convex combinations can also be used to interpolate polynomials. Start first with first order interpolations by interpolating the points with straight lines of the form $f_{k}(x):=m_{k}\cdot x+b_{k}$. Here, the points $\mathbb {D} :=\{(x_{0},y_{0}),\ldots ,(x_{n},y_{n})\}$ are given data points that are interpolated piecewise using the functions $f_{k}(x):=m_{k}\cdot x+b_{k}$. Compute from the convex combinations $P_{k}(t)\in \mathbb {R} ^{2}$ the functional representation $f_{k}:[x_{k-1},x_{k}]\to \mathbb {R}$ with $f_{k}(x):=m_{k}\cdot x+b_{k}$:

$P_{k}(t):=(1-t)\cdot {\begin{pmatrix}x_{k-1}\\y_{k-1}\end{pmatrix}}+t\cdot {\begin{pmatrix}x_{k}\\y_{k}\end{pmatrix}}$

Calculation of t as a function of x

Given $x\in [x_{k-1},x_{k}]\subset \mathbb {R}$. We now compute the corresponding $t\in [0,1]$ for the convex combination with the preliminary consideration that $t=0$ for $x=x_{k-1}$ and $t=1$ for $x=x_{k}$. The following figure takes the linear transformation $T:[x_{k-1},x_{k}]\to [0,1]$.

$T(x):={\frac {x-x_{k-1}}{x_{k}-x_{k-1}}}$

Calculation of the function value at x

The convex combination

$P_{k}(t):=(1-t)\cdot {\begin{pmatrix}x_{k-1}\\y_{k-1}\end{pmatrix}}+t\cdot {\begin{pmatrix}x_{k}\\y_{k}\end{pmatrix}}$

gives the interpolation point of the graph. However, we only need the y-coordinate of the corresponding interpolation point $P_{k}(t)={\begin{pmatrix}(1-t)\cdot x_{k-1}+t\cdot x_{k}\\(1-t)\cdot y_{k-1}+t\cdot y_{k}\end{pmatrix}}$. So we use the following term: $(1-t)\cdot y_{k-1}+t\cdot y_{k}$.

Functional representation

Substituting for $t\in [0,1]$ gives the linear interpolation function $f_{k}:[x_{k-1},x_{k}]\to \mathbb {R}$ over:

$f_{k}(x):={\bigg (}1-\underbrace {\frac {x-x_{k-1}}{x_{k}-x_{k-1}}} _{=t}{\bigg )}\cdot y_{k-1}+{\bigg (}\underbrace {\frac {x-x_{k-1}}{x_{k}-x_{k-1}}} _{=t}{\bigg )}\cdot y_{k}$.

Learning Tasks

• Calculate the coefficients $m_{k},b_{k}\in \mathbb {R}$ of the function $f_{k}:[x_{k-1},x_{k}]\to \mathbb {R}$ with $f_{k}(x):=m_{k}\cdot x+b_{k}$!
• Transfer this interpolation to convex combination of order 3 and consider how, depending on the data points, you must choose the two auxiliary points of the interpolation so that the interpolation is differentiable and generates differentiable transitions between the interpolation points in the plot.
• What geometric properties must auxiliary points between two adjacent interpolation intervals have for differentiability.

Interpolation with convex combination of order 3

See also

• convex combinations
• p-convex hull
• Mathematical modeling
• [convex combination interactive in GeogebraTube]
• Integration paths in function theory
• Hilbertraum
• [Convex combination and interpolation on triangles in the plane]
• Theorem of Rouché in functional theory
• polynomial algebra
• Bernstein polynomials
• Bezier curves
• De-Casteljau's algorithm
• Measure theory on topological spaces