Wright State University Lake Campus/2018-9/Phy1110/Notes
Mon 27 AugQB/a02 1Dkinem definitions
[edit | edit source]- QB/a02 1Dkinem definitions Class did all these questions in groups.
Wed 29 Aug Ohio State Coding
[edit | edit source]Extended content
|
|---|
*airhead-straw-cleaner: start by creating canvas 500x500 centers it.
Then, tell computer to draw by calling "function draw(){
fill }"
*Learned how define variable, but truggling with found an "variables are not functions"
One of the laptops had no internet access, but nevertheless an account was made.
one account
Big Group
fill and text size. Most seem to like it. Redshirt felt they made progress, which is impressive b/c Redshirt didn't know how to code.
Conclusion: This looks like a good project.
|
Wed 31 Aug 1D and 2D motion
[edit | edit source]QB/b_motionSimpleArithmetic and started QB/a03_2Dkinem_2dmotion
Wed 5 Sep Lab: Rolling ball (Excel)
[edit | edit source]| trial 2 | |
|---|---|
| t(s) | x(cm) |
| 0 | 0 |
| 1 | 36 |
| 2 | 70 |
| 3 | 109 |
| 4 | 157 |
We rolled a ping down a table that set and an angle 3.5/180 radian. starting at zero seconds, we measured the distance traveled. WE did the experiment three times and only one gave us a parabola.
A quick estimate of the epected acceralation was obtained by a best fit a parabola. We measured a=3.5 cm/s^2 but estimated[1] a≈20cm/s^2.
The class learned how to convert these date into velocity versus time.
Fri 7 Sep Quizzes
[edit | edit source]- Test is Wed 17 Sep 2018
2/4 from Special:Permalink/1828918 to QB/a02_1Dkinem_definitions
3/4 from Special:Permalink/1863423 to QB/a02_1Dkinem_equations
5/12 from Special:Permalink/1863384 to QB/b_motionSimpleArithmetic
3/4 from Special:Permalink/1863096 to QB/a03_2Dkinem_2dmotion
2/4 from Special:Permalink/1863115 to QB/a03_2Dkinem_smithtrain
Clueless about Mon but Wed 12 September ...
[edit | edit source]Half the class experimented and the other half conceptualized. All present on a half-finished lab.
14 September 2018 First effort by PHY1110 and 1050
[edit | edit source]All but the student supervisor were present, but we got by with a new boss. In HTW noRake (shovel) was absent.
-
click image to expand
-
click image to expand
| x | y |
|---|---|
| 0 | 0 |
| 21 | 10.8 |
| 32 | 24.5 |
| 39.5 | 40.2 |
| 46.5 | 65.5 |
| 54.2 | 98.1 |
| 55.5 | 123.7 |
| 57.7 | 147.3 |
| 57.7 | 179 |
12:59, 8 October 2018 (UTC)
[edit | edit source]7/19 from Special:Permalink/1863392 to QB/b_velocityAcceleration
1/4 from Special:Permalink/1863116 to QB/a04DynForce Newton_forces
2/4 from Special:Permalink/1863117 to QB/a04DynForce Newton_sled
2/5 from Special:Permalink/1863118 to QB/a04DynForce Newton_tensions
1/5 from Special:Permalink/1863119 to QB/a05frictDragElast_3rdLaw
2/5 from Special:Permalink/1863120 to QB/a06uniformCircMotGravitation_friction
16:00, 10 October 2018 (UTC)
[edit | edit source]Suggested project
[edit | edit source]For example
[edit | edit source]- π can be ascertained using a circle and a ruler. But we can look for a way to do it on a spreadsheet.
- e was discovered by Euler who was trying to model the explosion inside a cannon (or something like that...). But we can use a spreadsheet to "discover" using compound interest.
- i is a tough one. It is most easily defined through i2=−1, but I think we need to also prove that (−1)2 is not −1. That takes a little bit of geometry (easy to do).
- Given all this, you can write an Excel spreadsheet to show that eiπ≈−1 to very high precision.
Finding pi: https://www.youtube.com/watch?v=_rJdkhlWZVQ
Final_Project
[edit | edit source]Final Project: These problems are also available in OpenStax College Physics, which is licensed under a Creative Commons Attribution 4.0 License.[2]
The project covers chapters 8-15
[edit | edit source]- is momentum, where m is mass and is velocity. The net momemtum is conserved if all forces between a system of particles are internal (i.e., come equal and opposite pairs):
- .
- is the impulse, or change in momentum associated with a brief force acting over a time interval . (Strictly speaking, is a time-averaged force defined by integrating over the time interval.)
EXAMPLE 8.7 DETERMINING THE FINAL VELOCITY OF AN UNSEEN OBJECT FROM THE SCATTERING OF ANOTHER OBJECT Suppose the following experiment is performed. A 0.250-kg object (m1) is slid on a frictionless surface into a dark room, where it strikes an initially stationary object with mass of 0.400 kg (m2). The 0.250-kg object emerges from the room at an angle of 45.0º with its incoming direction.
- Problem 47 A 3000-kg cannon is mounted so that it can recoil only in the horizontal direction. (a) Calculate its recoil velocity when it fires a 15.0-kg shell at 480 m/s at an angle of 20.0º above the horizontal. (b) What is the kinetic energy of the cannon? This energy is dissipated as heat transfer in shock absorbers that stop its recoil. (c) What happens to the vertical component of momentum that is imparted to the cannon when it is fired?
- delete templates above

- is the torque caused by a force, F, exerted at a distance ,r, from the axis. The angle between r and F is θ.
The SI units for torque is the newton metre (N·m). It would be inadvisable to call this a Joule, even though a Joule is also a (N·m). The symbol for torque is typically τ, the Greek letter tau. When it is called moment, it is commonly denoted M.[3] The lever arm is defined as either r, or r⊥. Labeling r as the lever arm allows moment arm to be reserved for r⊥.
EXAMPLE 9.5 DO NOT LIFT WITH YOUR BACK Consider the person lifting a heavy box with his back, shown in Figure 9.30. (a) Calculate the magnitude of the force FB– in the back muscles that is needed to support the upper body plus the box and compare this with his weight. The mass of the upper body is 55.0 kg and the mass of the box is 30.0 kg. (b) Calculate the magnitude and direction of the force FV– exerted by the vertebrae on the spine at the indicated pivot point. Again, data in the figure may be taken to be accurate to three significant figures.
- Problem 14. A sandwich board advertising sign is constructed as shown in Figure 9.35 . The sign’s mass is 8.00 kg. (a) Calculate the tension in the chain assuming no friction between the legs and the sidewalk. (b) What force is exerted by each side on the hinge?
- Problem 15 refers to the previous question: (a) What minimum coefficient of friction is needed between the legs and the ground to keep the sign in Figure 9.35 in the position shown if the chain breaks? (b) What force is exerted by each side on the hinge?
| Linear motion | Angular motion |
|---|---|
The following table refers to rotation of a rigid body about a fixed axis: is arclength, is the distance from the axis to any point, and is the tangential acceleration, which is the component of the acceleration that is parallel to the motion. In contrast, the centripetal acceleration, , is perpendicular to the motion. The component of the force parallel to the motion, or equivalently, perpendicular, to the line connecting the point of application to the axis is . The sum is over particles or points of application.
| Linear motion | Rotational motion | Defining equation |
|---|---|---|
| Displacement = | Angular displacement = | |
| Velocity = | Angular velocity = | |
| Acceleration = | Angular acceleration = | |
| Mass = | Moment of Inertia = | |
| Force = | Torque = | |
| Momentum= | Angular momentum= | |
| Kinetic energy = | Kinetic energy = |
| Description[5] | Figure | Moment(s) of inertia |
|---|---|---|
| Rod of length L and mass m (Axis of rotation at the end of the rod) |

|
|
| Solid cylinder of radius r, height h and mass m | 
|
|
| Sphere (hollow) of radius r and mass m | 
|
|
| Ball (solid) of radius r and mass m | 
|
EXAMPLE 10.13 CALCULATING THE TORQUE IN A KICK The person whose leg is shown in Figure 10.22 kicks his leg by exerting a 2000-N force with his upper leg muscle. The effective perpendicular lever arm is 2.20 cm. Given the moment of inertia of the lower leg is 1.25 kg⋅m2, (a) find the angular acceleration of the leg. (b) Neglecting the gravitational force, what is the rotational kinetic energy of the leg after it has rotated through 57.3º (1.00 rad)?
- Problem 20. Unreasonable ResultsAn advertisement claims that an 800-kg car is aided by its 20.0-kg flywheel, which can accelerate the car from rest to a speed of 30.0 m/s. The flywheel is a disk with a 0.150-m radius. (a) Calculate the angular velocity the flywheel must have if 95.0% of its rotational energy is used to get the car up to speed. (b) What is unreasonable about the result? (c) Which premise is unreasonable or which premises are inconsistent?
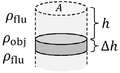
Pressure versus Depth: A fluid's pressure is F/A where F is force and A is a (flat) area. The pressure at depth, below the surface is the weight (per area) of the fluid above that point. As shown in the figure, this implies:
where is the pressure at the top surface, is the depth, and is the mass density of the fluid. In many cases, only the difference between two pressures appears in the final answer to a question, and in such cases it is permissible to set the pressure at the top surface of the fluid equal to zero. In many applications, it is possible to artificially set equal to zero, for example at atmospheric pressure. The resulting pressure is called the gauge pressure, for below the surface of a body of water.
Buoyancy and Archimedes' principle Pascal's principle does not hold if two fluids are separated by a seal that prohibits fluid flow (as in the case of the piston of an internal combustion engine). Suppose the upper and lower fluids shown in the figure are not sealed, so that a fluid of mass density comes to equilibrium above and below an object. Let the object have a mass density of and a volume of , as shown in the figure. The net (bottom minus top) force on the object due to the fluid is called the buoyant force:
- ,
and is directed upward. The volume in this formula, AΔh, is called the volume of the displaced fluid, since placing the volume into a fluid at that location requires the removal of that amount of fluid. Archimedes principle states:
- A body wholly or partially submerged in a fluid is buoyed up by a force equal to the weight of the displaced fluid.
Note that if , the buoyant force exactly cancels the force of gravity. A fluid element within a stationary fluid will remain stationary. But if the two densities are not equal, a third force (in addition to weight and the buoyant force) is required to hold the object at that depth. If an object is floating or partially submerged, the volume of the displaced fluid equals the volume of that portion of the object which is below the waterline.
EXAMPLE 11.10 CALCULATING DENSITY: IS THE COIN AUTHENTIC? The mass of an ancient Greek coin is determined in air to be 8.630 g. When the coin is submerged in water as shown in Figure 11.25, its apparent mass is 7.800 g. Calculate its density, given that water has a density of 1.000g/cm3 and that effects caused by the wire suspending the coin are negligible.
- Problem 39. If your body has a density of 995 kg/m3, what fraction of you will be submerged when floating gently in: (a) freshwater? (b) salt water, which has a density of 1027 kg/m3?

- the volume flow for incompressible fluid flow if viscosity and turbulence are both neglected. The average velocity is and is the cross sectional area of the pipe. As shown in the figure, because is constant along the developed flow. To see this, note that the volume of pipe is along a distance . And, is the volume of fluid that passes a given point in the pipe during a time .
- is Bernoulli's equation, where is pressure, is density, and is height. This holds for inviscid flow.
- converts from Celsius to Kelvins, and converts from Celsius to Fahrenheit.
- is the ideal gas law, where P is pressure, V is volume, n is the number of moles and N is the number of atoms or molecules. Temperature must be measured on an absolute scale (e.g. Kelvins).
- NAkB=R where NA= 6.02 × 1023 is the Avogadro number. Boltzmann's constant can also be written in eV and Kelvins: kB ≈8.6 × 10-5 eV/deg.
- is the average translational kinetic energy per "atom" of a 3-dimensional ideal gas.
- is the root-mean-square speed of atoms in an ideal gas.
- is the total energy of an ideal gas, where
EXAMPLE 13.3 CALCULATING LINEAR THERMAL EXPANSION: THE GOLDEN GATE BRIDGE The main span of San Francisco’s Golden Gate Bridge is 1275 m long at its coldest. The bridge is exposed to temperatures ranging from –15ºC to 40ºC. What is its change in length between these temperatures? Assume that the bridge is made entirely of steel.
- Problem 13. You are looking to purchase a small piece of land in Hong Kong. The price is “only” $60,000 per square meter! The land title says the dimensions are 20m×30 m. By how much would the total price change if you measured the parcel with a steel tape measure on a day when the temperature was 20ºC above normal?
Here it is convenient to define heat as energy that passes between two objects of different temperature The SI unit is the Joule. The rate of heat trasfer, or is "power": 1 Watt = 1 W = 1J/s
- is the heat required to change the temperature of a substance of mass, m. The change in temperature is ΔT. The specific heat, cS, depends on the substance (and to some extent, its temperature and other factors such as pressure). Heat is the transfer of energy, usually from a hotter object to a colder one. The units of specfic heat are energy/mass/degree, or J/(kg-degree).
- is the heat required to change the phase of a a mass, m, of a substance (with no change in temperature). The latent heat, L, depends not only on the substance, but on the nature of the phase change for any given substance. LF is called the latent heat of fusion, and refers to the melting or freezing of the substance. LV is called the latent heat of vaporization, and refers to evaporation or condensation of a substance.
- is rate of heat transfer for a material of area, A. The difference in temperature between two sides separated by a distance, d, is . The thermal conductivity, kc, is a property of the substance used to insulate, or subdue, the flow of heat.
- is the power radiated by a surface of area, A, at a temperature, T, measured on an absolute scale such as Kelvins. The emissivity, , is 1 for a black body, and 0 for a perfectly reflecting surface. The Stefan-Boltzmann constant is .
EXAMPLE 14.9 CALCULATE THE NET HEAT TRANSFER OF A PERSON: HEAT TRANSFER BY RADIATION What is the rate of heat transfer by radiation, with an unclothed person standing in a dark room whose ambient temperature is 22.0ºC. The person has a normal skin temperature of 33.0ºC and a surface area of 1.50m2. The emissivity of skin is 0.97 in the infrared, where the radiation takes place.
- Problem 64. Calculate the temperature the entire sky would have to be in order to transfer energy by radiation at 1000W/m2 —about the rate at which the Sun radiates when it is directly overhead on a clear day. This value is the effective temperature of the sky, a kind of average that takes account of the fact that the Sun occupies only a small part of the sky but is much hotter than the rest. Assume that the body receiving the energy has a temperature of 27.0ºC.

- Pressure (P), Energy (E), Volume (V), and Temperature (T) are state variables (state functionscalled state functions). The number of particles (N) can also be viewed as a state variable.
- Work (W), Heat (Q) are not state variables.
- , is the entropy of an ideal , monatomic gas. The constant is arbitrary only in classical (non-quantum) thermodynamics. Since it is a function of state variables, entropy is also a state function.

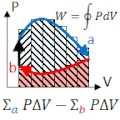
A point on a PV diagram define's the system's pressure (P) and volume (V). Energy (E) and pressure (P) can be deduced from equations of state: E=E(V,P) and T=T(V,P). If the piston moves, or if heat is added or taken from the substance, energy (in the form of work and/or heat) is added or subtracted. If the path returns to its original point on the PV-diagram (e.g., 12341 along the rectantular path shown), and if the process is quasistatic, all state variables (P, V, E, T) return to their original values, and the final system is indistinguishable from its original state.
The net work done per cycle is area enclosed by the loop. This work equals the net heat flow into the system, (valid only for closed loops).
Remember: Area "under" is the work associated with a path; Area "inside" is the total work per cycle.
- is the work done on a system of pressure P by a piston of voulume V. If ΔV>0 the substance is expanding as it exerts an outward force, so that ΔW<0 and the substance is doing work on the universe; ΔW>0 whenever the universe is doing work on the system.
- is the amount of heat (energy) that flows into a system. It is positive if the system is placed in a heat bath of higher temperature. If this process is reversible, then the heat bath is at an infinitesimally higher temperature and a finite ΔQ takes an infinite amount of time.
- is the change in energy (First Law of Thermodynamics).
CALCULUS: .
- In an isothermal expansion (contraction), temperature, T, is constant. Hence P=nRT/V and substitution yields,
- describes oscillatory motion with period (here we use the zero-subscript to denote constants that do not vary with time).
- . For example, .
- for a mass-spring system with mass, m, and spring constant, ks.
- for a low amplitude pendulum of length, L, in a gravitational field, g.
- is the potential energy of a mass spring system.
Let describe position:
- , where is maximum velocity.
- , where , is maximum acceleration.
- , relates maximum force to maximum acceleration.
- is the total energy.
- CALCULUS: x(t) obeys the linear homogeneous differential equation (ODE),

- relates the frequency, f, wavelength, λ,and the the phase speed, vp of the wave (also written as vw) This phase speed is the speed of individual crests, which for sound and light waves also equals the speed at which a wave packet travels.
- describes the n-th normal mode vibrating wave on a string that is fixed at both ends (i.e. has a node at both ends). The mode number, n = 1, 2, 3,..., as shown in the figure.
- Beat frequency: The frequency of beats heard if two closely space frequencies, and , are played is .
- Musical acoustics: Frequency ratios of 2/1, 3/2, 4/3, 5/3, 5/4, 6/5, 8/5 are called the (just) "octave", "fifth", "fourth", "major-sixth", "major-third", "minor-third", and "minor-sixth", respectively.
- is the the approximate speed near Earth's surface, where the temperature, T, is measured in Kelvins. A theoretical calculation is where for a semi-classical gas with degrees of freedom. For a diatomic gas such as Nitrogen, γ = 1.4.
- is the speed of a wave in a stretched string if is the tension and is the linear mass density (kilograms per meter).
How do we...
[edit | edit source]...allow group work?
[edit | edit source]Permit individual work or groups of 2 or 3 people, with the understanding that I expect more from groups.
...encourage covering of most (if not all) sections?
[edit | edit source]The first seven questions start at Fluid Statics. Do one problem from each section until you get to the end (Physics of Hearing)
...permit people to set up or explain problems without doing the actual calculation?
[edit | edit source]You must do at least X problems to the "bitter end". After that, it's up to you. If you need to actually do the calculation, you will receive credit for that effort. If you don't need the practice, I will take your word for it.
...organize the feedback?
[edit | edit source]What I prefer: You hand in something every day on white typing paper, with:
- Names on top 3/4 inch and 1/4 inch margin all around, and Public Domain statement inside.
- I make a copy and return the original to you.
- The rest of the course is devoted to you using this to "teach yourself the book".
Journal
[edit | edit source]Mon 26 Nov Fluid Statics and Fluid Dynamics
[edit | edit source]- It's OK to work on a spiral notebook and photocopy IF you find yourself wasting time doing it my way.
- Showed class: Buoyant Force problems 1 and 2. Defined pressure, P, as F/A where F is force and A is area. Pressure increases in depth as ρgh where ρ is mass density (mass/volume) and h is depth. Buoyant force is the net pressure force (i.e. between the top and bottom of a cylinder). It is also the weight of the displaced fluid.
- On Fluid Dynamics, you might just want to do the first problem. Other projects:
- Simple and elementary: Describe the blowing over paper demonstration
- Advanced: Explain why Q=Av, where Q is flow rate (volume/time), A is cross-sectional area, and v is flow rate. This is a beautiful thing to derive.
________________________________________________________________________________
Footnotes
[edit | edit source]- ↑ We need to do this calculation later in the cours
- ↑ © Nov 8, 2018 OpenStax College. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Under this license, any user of this textbook or the textbook contents herein must provide proper attribution as follows: The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the creative commons license and may not be reproduced without the prior and express written consent of Rice University. For questions regarding this license, please contact support@openstax.org. If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, College Physics. OpenStax CNX. Nov 8, 2018 http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@14.4. If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@14.4. If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@14.4.
- ↑ https://en.wikipedia.org/w/index.php?title=Torque&oldid=582917749
- ↑ "Linear Motion vs Rotational motion" (PDF).
- ↑ https://en.wikipedia.org/w/index.php?title=List_of_moments_of_inertia&oldid=582953751