Web Science/Part2: Emerging Web Properties/Emerging Structure of the Web

Home

Part1: Foundations of the web

Part2: Emerging Web properties

Part3: Behavioral Models

Part4: Web & society

Participate

About the Web Science MOOC

Course elements  

• PART1: Week1: Ethernet · Internet Protocol  · Week2: Transmission Control Protocol · Domain Name System · Week3: Internet vs world wide web · HTTP · Week4: Web Content  · Dynamic Web Content
• PART2: Week5: How big is the Web?  · Descriptive Web Models  · Week6: Advanced Statistic Models  · Modelling Similarity  · Week7: Generative Modelling of the Web · Graph theoretic Web Modelling
• PART3: Week8 : Investigating Meme Spreading  · Herding Behaviour  · Week9: Online Advertising  · User Modelling
• PART4: Week10 : Copyright  · Net neutrality  · Week11: Internet governance  · Privacy

6th week due Dec 2 nd December 3rd The Human Factor Core Propositions of this Lesson The Web is created by the people People use Web technologies Understanding the Web requires understanding, describing and predicting how people use Web technologies The lesson on Human Factor We have now learned a lot about the Web: Its basic protocols and languages, i.e. HTTP, HTML, CSS, but also media formats The network layers and protocols it builds on, i.e. Ethernet, IP, TCP, DNS How to program Web content, i.e. servlets and JavaScript By learning all this content, do we now know what the Web is? No! Not at all! A painter requires tools, such as canvas and colors, to create a painting. Once you know which type of canvas and colors are available, you still do not know what paintings an artist can and will create. Likewise, we now know what tools people have to create the Web, but we have not looked yet at the Web that the people actually have been creating. Ok, let's look at the Web. But, how should we look at the Web? As a parent, we may want to look at the Web to understand how it can further or harm our children. As someone who wants to be entertained, we may want to look at the Web to find amusement. As someone who works with the Web, we may want to understand how the Web helps us to do our work. As Web scientists, we look at the Web as an object of scientific investigation, we want to look at the underlying regularities. Now, that we have learned about the technical regularities, we need to understand how the people who create the Web do this, what factors constrain them or further them, i.e. how people interact with the Web. As Web scientists, we do not only want to look, but we want to describe. In order to describe the Web and the people in the Web we need to model both. A core challenge that we will encounter and that we have to deal with is that we cannot determine or predict the exact behavior of humans. Human behavior that we observe on the Web is random to quite some extent. That does not mean that it is arbitrary. Human behavior is constrained by what humans can do in the Web. And while we need to come up with models of human behavior that include randomness, such models will still lead to insight of human behavior at large. Example questions that we will try to answer by this method of "looking" and "describing" (or modelling) will include: Why is the Web not just a pure mess of unsorted documents? How can we exploit resulting structure of the Web - for technical purposes? How can we compare different situations that are more or less beneficial to Web users or Web platform operators? Quiz Who has created the Web? Tim Berners-Lee Vint Cerf Al Gore W3C IEEE Everyone Noone Randomness vs Regularities Core Propositions of this Lesson Humans cannot be predicted precisely, but some of their behavior can be captured in probabilistic models Randomness in probabilistic models leads to regularities in the Web The lesson on Randomness vs Regularities When we ask ourselves how can randomness lead to regularities, we may best look at an analogy. You may know the following example from your physics classes in high school: Assume that you have a box that is separated in two halves by a wall in the middle, the left half is empty, the right half contains millions of gas molecules. In the very moment when we take away the wall in the middle there is quite some order in the box, because all molecules are just in one of the two halves. When we take away the middle wall the molecules spread over both halves of the box and Boltzmann's law says that they will never ever again gather in one of the two halves. Hence, the previous order is destroyed, disorder is increased and the terminus technicus for the amount of disorder is called entropy. We can compute entropy - relative to being in one of the two halves - by determining the probability of gas molecules for being in one of the two halves and multiplying this probability with its logarithm and taking each state into account. If we'd assume that links in the Web would be forged in a completely random manner - just like the molecules spread arbitrarily between the two boxes - then the probability of linking from one particular Web page to another particular one should be the same for all pairs. As we will see later, however, this is not the case. Why not? Indeed we can model each person acting in the Web, i.e. surfing, creating Web pages, creating links between Web pages, in a behavioristic manner as a random process. We can model each human agent as picking randomly from a set of choices over time. However, when we model all actors in the Web, we must model carefully enough such that the probability distributions we observe empirically actually match what we derive from our theoretical model. What does it mean to "model carefully enough"? In our behavioristic random model of human behavior, we must take into consideration that beyond sheer random behavior human actors are constrained by the software they use. When an actor surfs the Web, the browser interface mostly suggests to her to follow one of the links on the Web page [point to later explanations of Random Surfer Model and Preferential Attachment] human actors are constrained by their cognitive abilities. When an actor sees a Web page, she is more likely to read the Web page top down and - in Western culture - from left to right and consequently, she is more likely to act on a link displayed in the upper left part of the Web page than in the lower right [point to the Duncan Watts experiments on music recommendations explained later] human actors see what other actors do. When an actor observes that another person, maybe even a recognized expert, is recommending an item, the human actor behaves according to sociological and psychological constraints and might, even unconciously decide to rely or at least not to deviate from a previous statement of another actor and behave accordingly [this is a model assumption for the tag imitation in the Cattuto and Dellschaft experiments]. human actors behave according to internal objectives and intentions. [...not sure yet what to cite here, maybe the classification of Strohmaier into describers and categorizers???] How can such models help us in understanding and forming the Web? Let me give another analogy: Imagine that you have a university campus in the morning after some heavy snowfall and before walkways could be cleared from snow. When at such a point students start to cross the campus they walk their paths according to different constraints: they have a destination they want to reach they prefer rather short ways they have some physical restrictions on how they can move, e.g. jumping very high is usually not feasible they have preferences on how they can move, e.g. though they can move sideways this is usually not done they tend to follow the footsteps of others What comes out very quickly to the observer are pattern of paths in the snow. When these patterns do not coincide with actual paths on a campus without snow, then one often observes informal paths over the grass indicating that the official paths tried to force the students onto an inconvenient route. When the patterns in the snow coincide with actual official walkways there is a good match between students' needs and the available paths. Likewise in the Web, we may find that there may be regularities within or between Web sites that conform badly or well to the behavior of its users and may determine the success of such a site and of a Web ecosystem. Quite often it is impossible to completely predict the emerging behavior of users, but trying to support it may lead to better systems [Later example: Cattuto and others observed that there is statistically significant information contained in the ordering of tags in delicious. This result is far from being self-evident. Folksonomy systems like bibsonomy do not represent such order, therefore they lack the capability to support the user] Let us now first talk about what we mean with a "model" and after that look at three example models of user behavior on the Web. Task One metaphor describes the Web as the largest library of our all times. Discuss which structures a library has and which of these structures do also exist in or for the Web (300 words) and which structures are available now that might not have been part of a traditional library. Quiz Which of the following items may constitute forces that might bring structure to the Web? Entropy Collaborative work Standards Search engine behavior Randomness of user behavior Users imitating users Distinguishing Descriptive and Predictive Models Core Propositions of this Lesson Distinguish descriptive and predictive models and how they may overlap Distinguish dependent and independent variables Prediction need not be the same as causality The lesson on Descriptive and Predictive Models Creating models in such different disciplines as physics, psychology or Web science is an art. The objective is to connect a phenomenon that occurs first and another phenomenon that follows later. The first phenomenon is usually called the independent variable and what follows is called the dependent variable. This naming applies that the following phenomenon is somehow derived or correlated with what was provided as an input. A connection between independent and dependent variables should either allow for making some predictions into the future (if possible), i.e. it should constitute a predictive model; or it should explain the causality of some situation, i.e. it should constitute a descriptive model. An example for a predictive model is given by HCI research that finds that people from different cultural backgrounds do not only prefer different styles of user interfaces, but they even work work more effectively with different styles of user interfaces (cf. [Katharina Reinecke, Abraham Bernstein: Improving performance, perceived usability, and aesthetics with culturally adaptive user interfaces. ACM Trans. Comput.-Hum. Interact. 18(2): 8 (2011)]. Finding this connection is very intriguing, even though it does not tell us why the independent variable, i.e. the user interface style, and the dependent variable, the working effectiveness, are connected. It allows us to predict the future, because if we know the style and the background of the user we can predict with some good probability that his effectiveness of working will be higher or lower than in other circumstances. An example for a descriptive model is given by the [double pendulum] where we exactly understand the physics of the mechanical movements and we can describe them with mathematical formulas. We can describe how the independent variables, i.e. location and velocity of the pendulum as well as gravity at this location, influence the dependent variables, i.e. subsequent locations and velocities of the pendulum, still we cannot predict the position of the double pendulum 10 seconds from now. Furthermore, we may have descriptive models with explanatory power that also allow us to make predictions into the future. For instance, Newton's laws explain the connection between gravity and velocity and allow us to predict how an apple falls onto the earth. In Web Science we are interested in these different types of models to improve our understanding of the situations we encounter on the Web, to predict what may happen in the (near) future, but also to understand the cases where our models exhibit some behavior where we will not be able to make meaningful predictions into the future - as it is the case for the double pendulum. Further Reading [New Evidence for the Theory of the Stork] Quiz Which of the following statements are true Descriptive models cannot predict the future Independent variables cannot be observed The definition of dependent and independent variables depends on the creator of a model Predictive models describe causality observed correlations lead to good predictive models A Model for Link Generation (Erdős–Rényi) Core Propositions of this Lesson Modeling is Abstracting from Details Good Models are Simple Models Must be Testable against Observations Lesson on a Model for Link Generation (Erdős–Rényi) Let us look at our first example of a descriptive model in Web science. The problem being given here is to predict how authors of Web content create links between Web pages over time. In general, the process of creating links is very complex. An author may: Write some text have the intention to link to some explanation Use a search engine Surf the search results and further pages Find something interesting and decide to link in some other place of his text Go back to his authoring tool, insert some new text as well as a hyperlink from this new text And the author may iterate through this procedure and work in a myriad of other ways when creating a link. When we want to come up with a model that tries to predict where the author will set a link, we cannot target all the myriad of steps that the author may take. In fact, it would even be methodologically unsound to do so. To have a good model, the model should be as small as possible and be based on as few assumptions as possible be testable against empirical observations If we cannot test the model, we will never know whether it is any good. If it comes with many assumptions it will only be applicable in very few situations. And, if it is very complex, it may describe the current set of observations, but it is unlikely to generalize to other situations, i.e. it will have less explanatory power. In order to come up with a model that we can analyze, we hence need to make simplifications: Leave away what we cannot observe (following behavioristic tradition) In the Web is is extremely difficult to understand automatically (i.e. without human intervention) the meaning of what is written on a Web page In the Web it is nearly impossible to observe what people write over time (step 1), what their intention is (step 2), what they type into a search engine (step 3; search engine operators know of course); how they surf search results (step 4); what they find interesting (step 5) In the Web it is possible, but difficult to observe the addition of Web pages and links over time (cf. e.g. Creating temporally dynamic web search snippets) In the Web it is easy to observe that a Web page exists, i.e. its URL points to an actual document, and links between Web pages exists, i.e. that there is a link from one document with a URL to another document with URL. Thus, this is the (only) basis for the model of preferential attachment. Now, each model has dependent and independent variables and a way how the two are related. In the model of preferential attachment, links are added over time. I.e. the link that is newly created is a variable that depends on what other documents and links existed before, i.e. the independent variable ("independent" in the sense that they are not captured by the model; if the model was a program function, we would call the independent variables the parameter of this function and the dependent variables the output of this function). But, hey, didn't we say that it was difficult to observe the Web over time. While it is (relatively) ease to make a snapshot of a sizable part of the Web, it is multiple times more difficult to know what the Web looked liked at different points in time in the past. Well, we can still come up with a meaningful *descriptive model* if we do not target the prediction of new specific links, but only a description of how many links exist between different classes of Web pages. Then, our model represents Web pages at all different ages and if the model is correct, it explains the structure of them all. Let's summarize at this point: We want to describe which links between Web pages are generated (such that the Web is not a complete mess) We only have one dependent variable: which link is created next. We have independent variables representing which Web pages exist and which are linked. We thus have few assumptions (because most assumptions we might not observe in any way in the first place) Thus, what remains to be done is: To come up with a simple model To test it against empirical observations Let us start with probably the simplest model of all where we just assume that we have n many web pages (each with a unique URL) and k many links between these pages, and k is less or equal than n*n. And, we can come up with a simple notation that says that each Web page is described by a number i or j between 1 and n and each link is described by a pair of numbers (i,j) where the pair means that Web page i links to Web page j. The model could foresee that the next link that is created is drawn randomly from all links that do not exist yet with the same probability, i.e. the probability that a link (i,j) that does not exist yet is created is 1/(n*n-k). This model is also known as the Erdős–Rényi model and many of its properties are described in the corresponding Wikipedia article. Pseudo code for this model may look like the following: Input: k number of nodes, l number of edges to be created 1 Initialize Int[][] edge to 0 in all entries indicating that there is no edge 2 FOR i=1 to l 3 n=random(1,k) 4 m=random(1,k) 5 IF (n=m) or edge(n,m)=1 6 THEN 7 i-- 8 ELSE 9 edge(n,m)=1 10 FI 11 ROF An example structure created looks like: Thus, we now have our first model for describing link generation. What we still do not know is whether this model is a good one. This will be the topic of our next lesson. Quiz 1 What do people produce on the Web and can be subject of scientific investigation and modelling? Bookmarks Classification Colors File extensions Geolocations Keywords, tags, hashtags Likes Metadata Numbers Playlists Words Other 2 How can hyperlinks be reasonably modelled? As a directed pair of two Web pages (links from .... to ...) As a triplet of anchor text and two Web pages (using text for hyperlink ... links from ... to ... ) As a quadruplet of anchor text and two Web pages and target anchor name (using text for hyperlink ... links from ... to ... targeting anchor of name ...) As a quintuplet of anchor text and two Web pages and target anchor name and link creator (using text for hyperlink ... links from ... to ... targeting anchor of name ... created by ...) Statistical Distributions for the Description of System Properties Core Propositions of this Lesson Gold-standard based evaluations focus on correctness of predictions Evaluations through statistical hypothesis testing compare observed statistical distributions against statistical distributions produced from the (probabilistic) model Distributions aggregate individual events, e.g. in-degree and out-degree distributions aggregate events of link creation Lesson on Statistical Distributions for the Description of System Properties How can we now test whether the Erdős–Rényi model is a good model for our problem? If Erdős–Rényi was a predictive model, we would apply a Cranfield-like (also called "gold standard-based evaluation") test setting: In such an evaluation setting a model is applied to a test dataset for which the correct answers are known (e.g. because human annotators have defined what are correct and incorrect answers or because we have historical data for which the outcome is known). Then one can check how often a prediction is correct and correspondingly derive different measures such as accuracy, precision and recall (and many more). Thus, one may evaluate the validity of a predictive model. In fact, in our lecture on Web Information Retrieval and Machine Learning and Data Mining, such Cranfield-like test settings are the core vehicle to compare the effectiveness of different models. In the case of the the Erdős–Rényi model (and in the case of many other, specifically, probabilistic descriptive models) we find however that The Erdős–Rényi model by itself does not do prediction about specific links between specific Web pages, but it only gives a - very low - probability for a link to be created. In fact, it is highly unlikely that there exist any model that could predict exactly (or frequently) the specific link that was to be created next. Much worse than in the case of the double pendulum, the factors that could determine *precisely* which link is created next are very insecure, as they ultimately reside in what a large mass of humans do - each of which is unpredictable on his/her own. 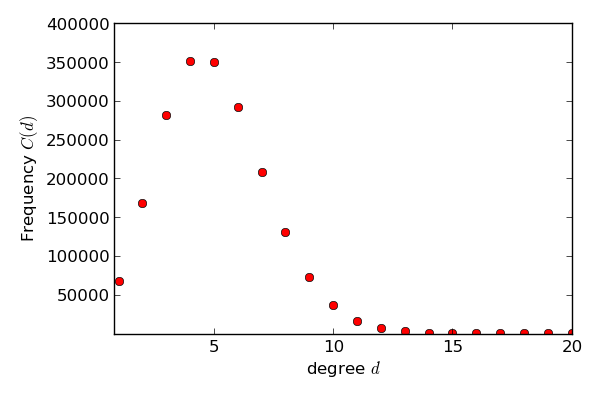What we may still do is to test whether we observe statistical distributions in the real world that we also find in our model. This is called Statistical Hypothesis Testing. Let us look at a classical distribution in networks, namely the *In-degree distribution*. The in-degree distribution is given by counting how many nodes (here each node is a Web page) have 0 links pointing to them, how many nodes have 1 link pointing to them, 2 links, 3 links and so forth. The result can be given in a table like this In-degree 0 1 2 3 4 5 6 7 8 9 10 Number of nodes with this in-degree 0 1 4 3 6 8 4 5 2 3 0 or in a histrogram like this: The idea behind statistical hypothesis testing in our setting is now that given one process that empirically produces a distribution (here: actual people creating links between Web pages) and another process that models the creation of the distribution (here: a model creating links according to simple rules like the Erdős–Rényi model), one compares the two distributions. This very idea is also depicted in the following figure. Let us consider the meaning of the 4 ovals in detail: Concerning the ovals "Observed Behavior in the Web" and "Statistics of Observed Behavior": The figure depicts the situation that behavior in the Web leads to an observable statistics. Sometimes the behavior itself is also observable, sometimes it is not. If we restricted our attention to Wikipedia, we would know rather precisely who created which link at which point in time *and* we could also derive all kind of statistics about link creations in Wikipedia. In the Web in general we do not know who created which link exactly when, but we only know some resulting statistics, e.g. the in-degree distribution of Web pages. Concerning the ovals "(Simulated) Probabilistic Model" and "Statistics of Probabilistic Model": When we have a probabilistic model (such as the Erdős–Rényi model) we may derive a statistical distribution in two ways: Preferably, we can analyse the model mathematically and compute an average distribution analytically (e.g. if we rolled a dice 60 times, we can analytically derive that each number from 1 to 6 appears an average of 10 times). Alternatively, if mathematical analysis becomes too complex, we may simulate the probabilistic model and count events in order to derive a statistical distribution. This may need iterations for the distribution to converge to averages. E.g. we could roll a dice, but we would have to roll it much more often than 60 times in order to accurately predict how often each number will show heads up. Finally, we need to compare the different distributions. What does "comparison" mean in this context? It could simply mean that the two distributions "look the same". In the following we will compare a distribution of in-degrees as counted from links in Wikipedia and we will compare this with a distribution of in-degrees as produced by the Erdős–Rényi model. But in order to find out about whether two distributions look the same, we actually have different diagramme types for this task. Such diagramme types applied to our scenario will be explained next. Quiz 1 Given this in-degree distribution: 0 1 2 3 4 5 6 7 8 9 10 0 1 4 3 6 8 4 5 2 3 0 How many nodes are in this network? 9 11 36 55 184 2 Given this in-degree distribution: 0 1 2 3 4 5 6 7 8 9 10 0 1 4 3 6 8 4 5 2 3 0 How many edges are in this network? 9 11 36 55 184 3 Why is an in-degree distribution of Web pages different from an out-degree distribution of Web pages? They are not different, but the same. Large numbers of out-degrees are less likely to occur than large numbers of in-degrees Large numbers of in-degrees are less likely to occur than large numbers of out-degrees Correct answer: 0+1+4+3+6+8+4+5+2+3+0=36 nodes 0*0+1*1+2*4+3*3+4*6+5*8+6*4+7*5+8*2+9*3+10*0 = 1+8+9+24+40+24+35+16+27 = 184 edges Different Diagramme Types for Statistical Distributions Core Proposition of this Lesson Distinguish linear functions, polynoms and exponential functions by choice of diagramme type 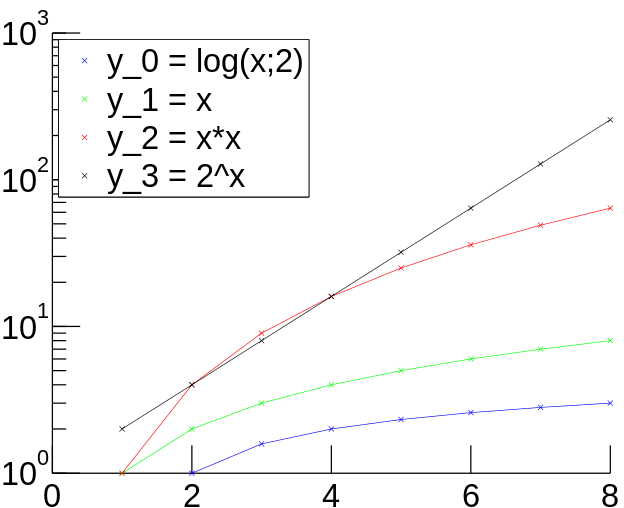Lesson on Different Diagramme Types for Probability Distributions We have already seen the simplest diagramme type, i.e. a histogramme of how many nodes with a specific in-degree exists given observations in the real world and in the a model. In such a diagramme we may depict absolute frequences, however, if we normalize such that all the different possibilities add up to probability one, we have to normalize our absolute counts by dividing each number by the overall number of events observed. No matter whether we compare absolute numbers or relative numbers, it frequently remains tricky to visually compare the different distributions. In the following you will see different (absolute) plots of different standard functions, ranging from logarithmic y=log(x;2), over linear y=x, over y=x*x quadratic function to exponential function y=2^x, and their inverses. A simple trick facilitates such comparisons: If we want to distinguish exponential functions from others, we can use a log-plot diagram. For any exponential function it holds that y=b^x, where b is the basis. If we plot log y instead of y, we effectively plot (log y)=log (b^x)=x*log(b), i.e. every exponential function appears as a straight line in a log-plot, while all other type of functions do not appear as such. The steepness of the function, i.e. the basis, is rendered by the steepness of (log b) of the straight line. 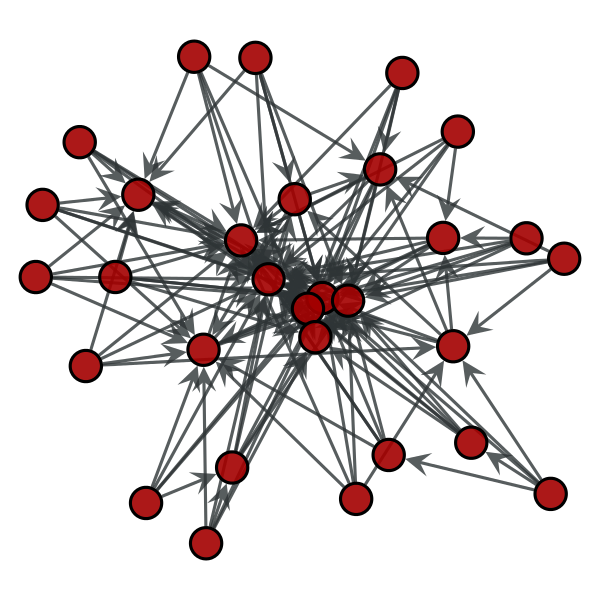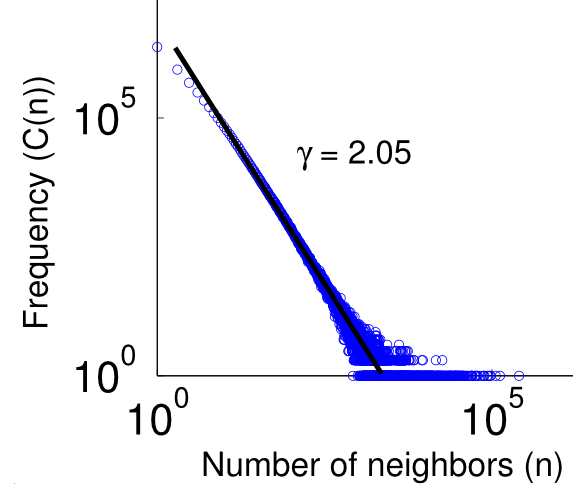Compare our functions from above in the following two log-plots: If we want to distinguish polynoms (or inverse polynoms), we can use a log-log-plot. For any polynom it holds: y=x^k. In a log-log-plot, we change the value we depict in the direction of the y-axis, but in addition we also change the plotting of values on the x-axis. This implies that instead of a pair of values (z,z^k) we plot the pair (log z, log (z^k))=(log z, k*log (z)). If we want to compute the value in y-direction for a given x=log z, we plot the value pair (x,y)=(log z, k*log(z))=(x,k*x). This means that in a log-log-plot diagram all polynoms (including linear functions) are depicted as straight lines, while other functions, such as exponentials or logarithms, are not straight lines. Compare our functions from above in the following two log-log-plots: We see now that be visual inspection alone we can already determine several interesting functions and their coefficients. Example Have a look at the following two graphs. This graph consists of 30 nodes and is a Random graph as described above. This graph also consists of 30 nodes. But it follows the rules of preferential attachment. Can you spot the difference? Let us assume we had a much bigger random graph with 2mio nodes. Drawing the graph is pointless but we can still plot the frequencies of the node degree. We might get the following picture: But is this what the web looks like? Let us look at the english wikipedia and take all articles as nodes and links between articles as edges and plot the degree distribution. We obtain the following picture: We see that the graphics don't look alike. But maybe that is due to the face that we used a log log scale so let us plot the random graph distribution on a log log scale: Still the graphs don't look alike. So we can all ready see that the web is not just a random graph but contains more structure. Let us have a look at the plot of graph that is generated using preferential attachment: The Graph is generated with 2 mio. nodes. Each node has 70 outedges. The generation model is preferential attachment. It has been plotted on a log log scale. It looks much more a like the distribution of our wikipedia network. Hence, what we observe about in-degree distributions of Web pages is that they follow a power law distribution, while Erdős–Rényi produces a Poisson distribution. Quiz 1 A logarithmic function, y=log x, appears as a straight line in... a standard diagramme a log plot a log-log plot an exponential plot no kind of diagramme 2 A complex polynom, e.g. y=3+x^1.5+x^7+x^11, appears as a straight line in... a standard diagramme a log plot a log-log plot an exponential plot no kind of diagramme Lesson on Some Useful Statistical Distributions and Quality Measures The audience may note that "looking the same" is not a mathematical proposition. In statistics mathematicians have created machinery in order to answer the following question: Given An empirical observation, e.g. a list of n numbers between 1 and 6, that lead to a distribution of which numbers between 1 and 6 have been generated how often, and A model, e.g. rolling a dice with six sides n times, how probable is it that the empirical observation was produced by the kind of dice of the model? Instead of rolling a dice, we may have a more complicated model and the empirical model may be more difficult, such as in our comparison of empirically observed in-degree distributions and in-degree distributions produced by a model, e.g. the Erdős–Rényi model. While it would be nice to go now into all the details of this comparison, this would require more time than we can have in this introduction to Web science. Those interested: more content in this direction will be given in the lecture on "Data Science" that will be given in the summer term 2014. The outcome of such a consideration will be the result that: it is highly unlikely that the Erdős–Rényi model produces some in-degree distribution as it is observed in the Web. Thus, in the next learning unit will we look for another model to describe link generation in the Web. Further Reading: Statistical Tools In our lecture on [Data Science] we will go into more details of computing statistics and determining the quality of a probabilistic model. In particular, we will look at a whole set of distributions: Uniform distribution Normal distribution Exponential distribution Power law distribution Poisson distribution Log normal distribution And we will look at quality measures such as: Students' t-test (valid only for normal distributions) Chi square ANOVA Kulback-Leibler and Jensen-Shannon Kolmogorov-Smirnov December 5th Let us summarize what we have achieved so far in this part: We have noted that part 1 covered the technical aspects of the Web, but not the creation process of Web content We have noted that we need to include human behaviour in our consideration, because human behavior determines what is created In fact, we can draw a picture like the following: The picture elaborates on what we have already used implicitly: A Human produces and consumes knowledge. Thereby his behavior is constrained by social norms, by his/her cognition, by his/her emotions, by his/her knowledge, etc. The same is true for all humans, but humans also observe what other people do in the Web What can be done - and what can be observed - in the Web is constrained: by protocols by applications by available data and information and last, but not least, by Web governance and legal laws More specifically, we have in our Web science model now abstracted quite a lot, but then came up with ideas of how we can build and validate models: We have found that modeling human behavior in the Web requires to model some form of randomness that reflects what we cannot observe, namely the human way of making a decision. We have taken as a running example the creation of links in the Web and we have reduced it to the bare minimum, namely the introduction of an edge between two nodes - abstracting from almost everything in the Web world. (Of course keeping what is core to the Web, i.e. the links). For this extremely simple world, we have developed a model to mimic the creation of links in the Web, i.e. the Erdős–Rényi model: It is a probabilistic model that creates a new link in completely random fashion between a pair of nodes. Then we have considered how to evaluate the quality of the model. We arrived at the idea of statistical hypothesis testing and we introduced a very simplistic model, i.e. the overlaying of plots. For this purpose we learned how to identify different types of distributions by modified coordinate axes of a plot (log-plots and loglog-plots). We found that what we observe for the Web (i.e. at least Wikipedia) does not easily match what is produced by the Erdős–Rényi model with regard to a very simple distribution: i.e. the in-degree distribution. What we have not seen in our models yet, is the mimicking of other behavior, as this was not part of the Erdős–Rényi model. In fact, we will see next that this is exactly what has been missing from the Erdős–Rényi model. Preferential Attachment as an Improved Model for Link Generation Core Propositions of this Lesson Know the Model for Preferential Attachment Understand why and how it is a better model for link creation than Erdős–Rényi Lesson on Preferential Attachment as an Improved Model for Link Generation The core idea of preferential attachment is that popular nodes attract more links that less popular nodes, i.e.: Popular people will attract more additional people who will know of them than less popular people (cf. the number of followers that people like Lady Gaga or Barack Obama have on twitter vs. the number of followers of Steffen Staab) Popular movies will have more new viewers than less popular movies Popular Web pages will be linked more often in the future than less popular Web pages Let us consider the issue of Web pages. Given a Web page, this is a node n, we formulate that the probability that the next link that is created points at this node n is proportional to the number of links that already point to n, i.e. the in-degree(n): $P(n)\sim {\text{in-degree}}(n)$ The original model of preferential attachment by Barabási and Albert only considers new nodes that join the network. To make it more easily comparable against the Erdős–Rényi model, we adopt their idea (like others have done) and say that the probability that a link is created from a node n to a node m, i.e. P(n,m), is proportional to each of them being selected: $P(n,m)\sim P(n)*P(m)$ We need a slight adaptation, because the probability of an unlinked node to be linked should not be zero, hence let us assume that a revised probability for selecting one node was: $P(n)\sim {\text{in-degree}}(n)+1$ Considering that P(n) must be a probability distribution we need to have a normalization factor Z $Z=k+\sum _{n=1}^{n=k}{\text{in-degree}}(n)$ such that $P(n,m)=({\text{in-degree}}(n)+1)*({\text{in-degree}}(m)+1)/(Z*Z)$ Then pseudo code for (our slightly modified) preferential attachment may look like: Int Pick() Helper functions: in-degree(n), Z() as defined above; random(1,z) returns an integer between 1 and z 1 n=1, c=0 2 z=Z() 3 t=random(1,z) 4 WHILE c<z DO 5 { c=c+in-degree(n)+1 6 n++ 7 } 8 RETURN n PrefAttachment(k,l) Input: k number of nodes, l number of edges to be created 1 Initialize Int[][] edge to 0 in all entries indicating that there is no edge 2 FOR i=1 to l 3 { n=Pick() 4 m=Pick() 5 IF (n=m) or edge(n,m)=1 6 { i-- } 7 ELSE 8 { edge(n,m)=1 } 9 } References Albert-László Barabási, Réka Albert. Emergence of Scaling in Random Networks. In: Science, 286 no. 5439 pp. 509-512, DOI: 10.1126/science.286.5439.509. Also available as preprint from http://arxiv.org/abs/cond-mat/9910332 Quizzes Which of these statements are true? probabilities represent how often events have been observed in an experiment a histogram represents how often events have been observed in an experiment the values of a probability distribution add up to 1 the values of a histogram add up to 1 Critical Assessment of Preferential Attachment Learning Objectives Further criteria for quality of a model: stability, coverage, generalizability, missing aspects Lesson on Critical Assessment of Preferential Attachment We have now seen two models for explaining link creation in the Web: Erdős–Rényi and preferential attachment. While the latter seems to be a better explanation for what is going on there are indeed questions that arise that have to do both with the mathematical background as well as with the emergence of power laws in many link creation scenarios, not only in the Web, but e.g. in citation networks (scientific papers cite older scientific papers; nodes, i.e. new papers, are only added but never destroyed; links, i.e. citation edges, are only added but never destroyed): susceptibility of coefficients (e.g. sub-linear attachment rates do not lead to power laws) Web pages and links are not only created, but also destroyed, still power laws of in-degrees emerge if power laws emerge in similar but different scenarios their creation mechanism under these other scenarios might more likely follow a similar mechanism timing (busy nodes do not only get more links, but they get more links more often) Hence, what we can observe here is a fundamental critique of the model that considers assumptions such as stability of achieved model under slightly changing assumptions (slightly different assumptions may lead to qualitatively different results) coverage of phenomena modelled (destruction remaining unhandled) generalizability (part of the beauty test of a model) time-dependency of the model unmodelled Some of that critique has been nicely formulated in by Hans Akkermans leading to further research and insights - more than we can handle in this lecture. Beyond, more criteria for critique may be uttered (Also by Akkermans). References Hans Akkermans: Web dynamics as a random walk: how and why power laws occur. WebSci 2012: 1-10. doi 10.1145/2380718.2380719 Diomidis Spinellis. The decay and failures of web references. In: Communications of the ACM, 46(1), pp. 71-77, 2003. doi 10.1145/602421.602422 Word/Tag production models Learning Objectives Learn to generalize From preferential attachment to (different) urn models From one model (preferential attachment) to other model (word production) Lesson on Word/Tag production models Models of word occurrences Reason to use tf-idf to describe word relevance of a page Models of folksonomies Zipf distributions models of word/tag distributions models of word/tag coocurrences Preferential Attachment OR Word Production (Polya Urn Model) There are n balls with different colors in an urn In each step: Randomly draw a ball Put it back together with a second ball of the same color Fixed number of colors Colors are distributed according to a power law Linear Preferential Attachment OR Word Production with Growing Vocabulary (Simon Model) Like the Polya Urn Model. Additionally in each step: Instead of drawing a ball, insert with low probability p a ball with a new color Linear increasing number of colors Colors are distributed according to a power law Further Readings about the Family of Poly Urn Models Read more about the Polya Urn Models (or Polya Processes) at [1] The Web as a Medium for Social Capital We now have (extremely simplistic) models of the Web that describe how content is formed and how links are created - and this is the core of Web content in the Web 1.0: Text and hyperlinks. While we can think about how to extend our models to more sophisticated content (media documents, dynamic content), and to some very, very small extent this is done in the literature (much more should be possible), we should sometimes also take a high-level view and consider how people decide to interact with a particular piece of Web content. Considering that Web content is produced by people and for people, it makes sense to consider the interaction of people via the Web also in sociological terms. While many disciplines have thought about how a medium is used to socially interact e.g. philosophy (language games, Wittgenstein), artificial life (language games, Luc Steels et al), linguistics, media sciences, anthropology, etc, we have now selected a theory that has its roots in sociology and management science, i.e. the notion of social capital. In Wikipedia it is stated that "In sociology, social capital is the expected collective or economic benefits derived from the preferential treatment and cooperation between individuals and groups." In the Web we have a knowledge system consisting of documents and links (I abstract here from important dimensions like transactions) and in this knowledge system, actors navigate, interact, grow the knowledge network, and parts of the knowledge network are more successful than others. Social capital is distinguished by Nahapietund Ghoshal(1998; http://www.jstor.org/stable/259373) into cognitive social capital, knowledge of vocabulary, narratives, etc. structural social capital, e.g. centrality, prestige, etc. relational social capital, e.g. trust, social norms, reciprocity This can be easily carried over to the Web, where a Web page has vocabulary and styles that it shares with other (sets of) Web pages; depending on the vocabulary used, the Web page may be more or less influential in the reception of people and allow for more knowledge creation than others is structurally linked to other Web pages; depending on its embeddedness, the Web page may be more or less influential in the reception of people and lead to more (or less) knowledge creation than others is trusted more or less and triggers more actions by others (reciprocity) and hence is more or less influential. Effectively, it is of course the person (or the institution) that has such higher social capital, but the Web page (or Web site) is the medium that carries the content and that leads to the increased benefit for the social actor. We can now try to determine: What vocabulary makes a Web page important or - a slightly reworded, but easier question - when does one determine that a word is well represented by a Web page? Which kind of links make a Web page important - this we will look at in the Random Surfer model in the Part about Search Engines What determines the relational value of a Web page (or a smaller entity, e.g. a Web message), i.e. triggering reciprocity or other kinds of actions, having reputation etc. Cognitive Social Capital: The Example of Measuring How Relevant a Term is for Representing a Document Cognitive social capital captures to which extent the expertise to use vocabulary, narratives and other cognitive "tools" in a social group constitutes capital for the individual, because he/she is better able to communicate and share ideas When is a word important or relevant? Or: How important is a word for representing a document? First try: Words that occur most often are most important: ${\text{tf}}(t,d)=$the frequency of term $t$ (word) in document $d$ Problem: What are the most important words now? a the and etc. According to this account they would be most important, because they are most frequent. So, should we rather go for the least frequent words, this would mean the ad-hoc invented words would be most useful - this cannot be true, because no common speaker of English (and English only) understands a word like "grlp". Obviously neither the most frequent nor the least frequent words are helpful in grouping (the technical term is "clustering") documents of a kind together and separating documents of a kind from documents of other kind. A word that helps to do exactly this should obviously not appear in all documents, but rather in a large, but not too large set of documents. Hence, one arrive at the idea of ${\text{idf}}(t,D)=-\log {\frac {N}{{\text{df}}(t,D)}}$the inverse frequency of how often a term $t$ appears in a set of Documents $D$ The combination of the two is then a balanced account between the two. In fact, there is not one formula striking such a balance, but a family of formulas, the most common of which is the following: ${\text{tfidf}}(t,d,D)=-{\text{tf}}(t,d)\cdot \log {\frac {N}{{\text{df}}(t,D)}}$ where N is the number of documents The following table describes the frequencys of english words in the Wikipedia as of November 4th 2013. Data set can be downloaded from http://dumps.wikimedia.org/enwiki/20131104/enwiki-20131104-pages-articles.xml.bz2 more information on http://dumps.wikimedia.org/enwiki/20131104/ word lowercase uppercase combined the 72417452 12441081 84858533 a 24087901 1456115 25544016 university 105779 816008 921787 science 118952 103846 222798 web 56653 20603 77256 frequency 37181 1653 38834 Koblenz 1 1296 1297 supercalifragilisticexpialidocious 2 19 21 References S. Robertson and H. Zaragoza. The Probabilistic Relevance Framework: BM25 and Beyond. Foundations and Trends in Information Retrieval. Vol. 3, No. 4 (2009) 333–389, 2009, DOI: 10.1561/1500000019 [2] Relational Social Capital: The Example of Meme Spreading What is a meme? Let's look back at what is a gene and what is its basic mechanism: A gene is information (e.g. DNA or RNA) And to be successful, genes need a replication mechanism. In biological life, the gene information is contained in a cell and the cell either actively replicates the gene information generating a new cell (e.g. an egg cell) or it is contained in a cell that makes sure to replicate it by another way (e.g. a virus). Further replication mechanisms exist (e.g. for prions). A meme is an idea, behavior, or style that spreads from person to person within a culture (cf. Meme in Wikipedia). In order for an idea to spread it needs some replication mechanism. People spread ideas in a culture by different ways, e.g. through gossip, or because people want to warn each other. The individual reason for replication may be selfish, it may be altruistic, etc. Like a gene, replication need not be perfect, and in fact copying mistakes occur. Hoaxes are memes that spread via email or in social networks, because people believe, e.g., the warning that is in a hoax and want to warn their friends, too, and with sending the hoax to everyone the hoax keeps alive frequently over many years - or it reappears in a slightly different shape after some years. The investigation of hoaxes on the Web is an interesting topic (I cannot find the paper about it anymore --SteffenStaab (discuss • contribs) 16:28, 4 December 2013 (UTC)) In twitter, hashtags have been invented by users in order to mark specific and often complicated keywords in their messages. Quite frequently now hashtags are considered to be simple memes and people investigate models that explain how such memes spread in a network like Twitter (people imitating other people's behavior). For this you need to know the basic functions of microblogging platforms like Twitter. Core are: Twitter is a social network with directed "follows" edges. This means that a person can follow every other person (or account) without the need for permission. Just like in the Web there are people who are particularly popular, e.g. the account of Obama has over 40 Mio followers as of Dec 15, 2013 (note: it is not a personal account). Persons can send tweets of 140 characters to their followers that see a timeline of most recent tweets arriving. Followers who receive a tweet may use the "retweet" button in order to spread the message. Alternatively, the person may decide to use some established abbreviations to denote that a tweet he/she send actually originates from a different account, e.g. saying "RT @ststaab" to describe that some content was coming from Steffen Staab (the retweet button does this automatically for the person) There are now several ways in which information diffusion may happen in the network. Retweeting is one. Another one is that messages contain hashtags, but people decide not to retweet the whole message, but just to reuse the hashtag and spread a somewhat different message. The interesting point in analysing either is that one achieves a picture of what content is deemed interesting by actual users (Note there are also many bots active in twitter that fake the presence of humans for such tasks as spamming, increasing the number of followers, etc.). Looking back at our original objective of this learning unit: we want to understand relational social capital. That is we want to understand the judgement that account holders exert in order to decide whether to disseminate information or now. Such judgement may be based on various criteria, such as spreading most trustworthy information, spreading most interesting information, spreading information for selfish reasons (e.g. making yourself look good), etc. etc. While all these are very hard to judge, what Weng et al suggest with their study is that: The technical platform provides users with input. The structure of the network and the scarcity of available user attention already allows for modeling information diffusions effects. User attention: Depending on how many followers you have you can see more or less of their tweets. If you follow 10,000 people that all tweet once a day, you will not be able to read all the tweets just for lack of time. Network structure: "Economy of attention" was first theoretized by H. Simon, nobel prize winner, economist and computer scientist: He came up with the notion of "satisficing reasoning", i.e. humans do not aggregate all available evidence, but they tend to focus on one or two criteria and make a choice based on the perceived value according to these criteria, e.g. when buying products people tend not to value all features of a product, but just one or two most salient ones. USE FIGURE 1 FROM (L. Weng, A. Flammini, A. Vespignani and F. Menczer) IF POSSIBLE. Relational Social Capital: A Model for Memes Spreading (Information Diffusion) The breadth of attention of a user Shannon's entropy measures how man bits are needed in order to write down all the events that are possible in an optimal encoding. To formulate it in very different words, the same entropy measures how much uncertainty is involved when observing a distribution of events. If there is a lot of uncertainty the amount of information needed to reflect this is high. If there is little uncertainty, one needs only very little information to represent the distribution of events. The measure considers the probability of an event or a piece of information to happen: $S=-\sum _{i}p(i)\cdot \log _{2}p(i)$ This formula reflects that events that occur all the time, i.e. their probability is close to 1, do not contribute much to entropy because of $\log _{2}1=0$. Likewise, events that occur only rarely, i.e. their probability is close to 0, do not contribute much to entropy. Hence, if two events are possible (e.g. throwing a coin with Head and Tail), but Head occurs with probability 1 and Tail with probability 0, the resulting entropy in this system is 0, reflecting the fact that their is no uncertainty involved. If the two events occur with uniform distribution, i.e. p(Head)=p(Tail)=0.5 then entropy is maximized, S=1. I.e. one needs one full bit to represent whether the one or the other event has happened. This may be generalized to n events. n events with uniform distribution have entropy $S=-\log _{2}{\frac {1}{n}}=\log _{2}n$. When we are now interested in a set of events, such as memes, where each meme is a hashtag and the probability that the user generates a meme is approximated by counting (and normalizing) how often he has used a particular hashtag, we may define the breadth of attention of a user by the same formula for entropy. User Interests The interests of a user can be represented by the activities that she has engaged in. If there are k memes that have been tweeted so far and user u has tweeted or retweeted l<k of them, we can represent this by: $I_{u}:=[...\sigma _{i}...],{\text{ where }}\sigma _{i}=1{\text{ if }}u{\text{ has retweeted that meme in the past and 0 otherwise }}$ ADD EXAMPLE Likewise, we can model a tweet by the set of memes (i.e. hashtags) it includes: $T_{n}:=[...\sigma _{i,n}...],{\text{ where }}\sigma _{i}=1{\text{ if }}T{\text{ contains the meme and 0 otherwise }}$ Similarity Cosine References L. Weng, A. Flammini, A. Vespignani and F. Menczer. Competition among memes in a world with limited attention. In: Sci. Rep., 2(335), 2012. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3315179/ Structural Social Capital: The Example of Random Surfer Model - The Generative Model Learning Objectives What makes a Web page important? How is such importance evoked by the Web structure itself? How to model with Lesson on Random Surfer When we consider the behavior of a person surfing the Web, the person has a number of choices to make, namely he may: Start on an arbitrary Web page Read the Web page Interact with the Web page (e.g. fill a form) Use the BACK-button Follow a link from that page OR Jump to another page by whatever mechanism (typing a URL, using a search engine, using a bookmark, etc. etc.) And maybe you can even come up with some more choices. Structural Capital: The Example of Random Surfer Model - The Analytical Model Learning Objectives Randomized models may be accessible for analytical solutions Vectors are good for representing the state of complex systems Matrices are good for representing networks representing transition probabilities Lesson on Random Surfer - The Analytical Model Represent transition probabilities as a matrix This is an ergodic Markoff system The solution is given by First eigenvalue of the corresponding equation The corresponding eigenvector gives the stationary probabilities of the surfer. But: don't solve analytically, but by iteration and by computing in distributed fashion This model has been crafted and exploited by Sergej Brin and Larry Page, the Google founders, in their PageRank algorithm in 1998. Cf. http://infolab.stanford.edu/pub/papers/google.pdf There are many modifications of this model, e.g. an intentional surfer model, rather than a random surfer, leading to improved rankings in certain situations, cf. http://pr.efactory.de/e-pagerank-themes.shtml. Further Thoughts on Research Needed Most research about Web structure focuses on static HTML pages and folksonomies (sometimes with time stamps of data). There is very little research on Web structure analysis looking at dynamic content. The reason is that there are very few people who understand both dynamic Web content and Web structure analysis and models. If you can think about some nice hypothesis, this could lead to intriguing research.

The structures described up to here have started to arise in the very early Web; very many structures however came into existence in order to be found. Thus, understanding the search engine eco system is important to understand the Web as it is now.

The following video of the flipped classroom associated with this topic are available:

You can find more information on wiki commons and also directly download this file

You can find more information on wiki commons and also directly download this file