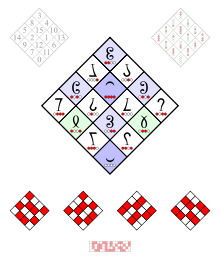
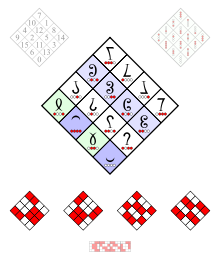
Multigrade operator XOR The magic square corresponding to wp ( 7,11,13,14), below the dual matrix
There are 24*9=216 Walsh permutations that correspond to magic squares of order 4.
5 7 10 11
5 7 10 14
5 7 11 13
5 7 13 14
5 10 11 13
5 10 13 14
7 10 11 14
7 11 13 14
10 11 13 14
RevCoLex order of the permutations.
I II III IV V VI
11 13 5 10
11 5 13 10
13 11 5 10
5 11 13 10
13 5 11 10
5 13 11 10
11 13 10 5
11 5 10 13
13 11 10 5
5 11 10 13
13 5 10 11
5 13 10 11
11 10 13 5
11 10 5 13
13 10 11 5
5 10 11 13
13 10 5 11
5 10 13 11
10 11 13 5
10 11 5 13
10 13 11 5
10 5 11 13
10 13 5 11
10 5 13 11
7 5 14 10
7 5 10 14
5 7 14 10
5 7 10 14
7 14 5 10
7 10 5 14
5 14 7 10
5 10 7 14
14 7 5 10
10 7 5 14
14 5 7 10
10 5 7 14
7 14 10 5
7 10 14 5
5 14 10 7
5 10 14 7
14 7 10 5
10 7 14 5
14 5 10 7
10 5 14 7
14 10 7 5
10 14 7 5
14 10 5 7
10 14 5 7
7 11 13 14
11 7 13 14
7 13 11 14
11 13 7 14
13 7 11 14
13 11 7 14
7 11 14 13
11 7 14 13
7 13 14 11
11 13 14 7
13 7 14 11
13 11 14 7
7 14 11 13
11 14 7 13
7 14 13 11
11 14 13 7
13 14 7 11
13 14 11 7
14 7 11 13
14 11 7 13
14 7 13 11
14 11 13 7
14 13 7 11
14 13 11 7
7 11 13 5
7 11 5 13
11 7 13 5
11 7 5 13
7 13 11 5
7 5 11 13
11 13 7 5
11 5 7 13
13 7 11 5
5 7 11 13
13 11 7 5
5 11 7 13
7 13 5 11
7 5 13 11
11 13 5 7
11 5 13 7
13 7 5 11
5 7 13 11
13 11 5 7
5 11 13 7
13 5 7 11
5 13 7 11
13 5 11 7
5 13 11 7
7 11 14 10
11 7 14 10
7 11 10 14
11 7 10 14
7 14 11 10
11 14 7 10
7 10 11 14
11 10 7 14
14 7 11 10
14 11 7 10
10 7 11 14
10 11 7 14
7 14 10 11
7 10 14 11
11 14 10 7
11 10 14 7
14 7 10 11
10 7 14 11
14 11 10 7
10 11 14 7
14 10 7 11
10 14 7 11
14 10 11 7
10 14 11 7
13 5 14 10
5 13 14 10
13 5 10 14
5 13 10 14
13 14 5 10
5 14 13 10
13 10 5 14
5 10 13 14
14 13 5 10
14 5 13 10
10 13 5 14
10 5 13 14
13 14 10 5
5 14 10 13
13 10 14 5
5 10 14 13
14 13 10 5
14 5 10 13
10 13 14 5
10 5 14 13
14 10 13 5
14 10 5 13
10 14 13 5
10 14 5 13
wp (11,13, 5,10)
wp (14, 7, 5,10)
wp (13,11,14, 7)
wp (13,11, 7, 5)
wp (14, 7,11,10)
wp (10, 5,13,14)
There are 24*81=1944 Walsh permutations that correspond to semi-magic squares of order 4 (where the diagonals do not necessarily sum up to 30).
5 6 7 9
5 6 7 10
5 6 7 11
5 6 7 13
5 6 7 14
5 6 7 15
5 6 9 11
5 6 9 13
5 6 9 14
5 6 10 11
5 6 10 13
5 6 10 14
5 6 11 15
5 6 13 15
5 6 14 15
5 7 9 10
5 7 9 13
5 7 9 15
5 7 10 11
5 7 10 14
5 7 11 13
5 7 11 15
5 7 13 14
5 7 14 15
5 9 10 11
5 9 10 13
5 9 10 14
5 9 11 13
5 9 11 15
5 9 13 14
5 9 13 15
5 9 14 15
5 10 11 13
5 10 13 14
5 11 13 15
5 13 14 15
6 7 9 10
6 7 9 11
6 7 9 13
6 7 10 14
6 7 10 15
6 7 11 14
6 7 11 15
6 7 13 14
6 7 13 15
6 9 10 11
6 9 10 13
6 9 10 14
6 9 11 14
6 9 13 14
6 10 11 14
6 10 11 15
6 10 13 14
6 10 13 15
6 10 14 15
6 11 14 15
6 13 14 15
7 9 10 11
7 9 10 15
7 9 11 13
7 9 11 15
7 9 13 15
7 10 11 14
7 10 11 15
7 10 14 15
7 11 13 14
7 11 13 15
7 11 14 15
7 13 14 15
9 10 11 13
9 10 11 14
9 10 11 15
9 10 13 15
9 10 14 15
9 11 13 14
9 11 14 15
9 13 14 15
10 11 13 14
10 11 13 15
10 13 14 15
11 13 14 15