Lexicographic and colexicographic order
Lexicographic (Lex) and colexicographic (CoLex) order are probably the most important ways to order tuples in mathematics.
Lex order is that of a dictionary.
CoLex order is obtained by reflecting all tuples, applying Lex order, and reflecting the tuples again.
Lex order is more intuitive for most people.
CoLex order is more practical when the finite sets of tuples to be ordered shall be generalized to infinite sets of sequences.
Both orderings can be reversed, so there are actually four different orderings.
They can also be reflected (see here), but that's not a different ordering of the set of tuples, but just a certain ordering written in a different way.
When the set of tuples contains all reflections, each reflected order is equal to some of the four others (see below).
Combinations
[edit | edit source]The sequence of the k-subsets of in CoLex order
is the beginning of the infinite sequence of k-subsets of in CoLex order.
This corresponds to the increasing sequence ![]() A014311 = 7,11,13,14,19,21...
A014311 = 7,11,13,14,19,21...
In the file on the left it can be seen that the blue patterns are horizontally reflected.
However, this is not the case in the file on the right, which shows only some of the subsets.
| Combinations with repetition |
|---|
 (red vectors RevLex, combinations Lex) |

The triangle on the right shows 2-subsets of the integers.
This corresponds to the sequence ![]() A018900 as a square array.
A018900 as a square array.
The sequence of numbers (3,5,6,9,10,12...) corresponds to the CoLex ordering of 2-subsets: (1, 2), (1, 3), (2, 3), (1, 4), (2, 4), (3, 4)...
| The 28 2-subsets of {1..8} |
|---|
1 2
1 3
2 3
1 4
2 4
3 4
1 5
2 5
3 5
4 5
1 6
2 6
3 6
4 6
5 6
1 7
2 7
3 7
4 7
5 7
6 7
1 8
2 8
3 8
4 8
5 8
6 8
7 8
|
Permutations
[edit | edit source]Finite sets of permutations are often shown in lex order, but rev colex order has the advantage that it can be used to order an infinite number of permutations.
This above all means the finitary symmetric group on , which is the union of all finite symmetric groups, and thus contains each finitary permutation of .
Its n-th element (counted from 0) is found in row n of ![]() A055089.
A055089.
This makes it possible to assign a number to a permutation that is only given in cycle notation, without seeing it as a permutation of a particular number of elements.
The reverse colex rank is its left inversion count interpreted as a (little-endian) factorial number.
The reverse colex order of the permutations corresponds to the colex order of these left inversion counts, as seen in the following illustrations.
 that have a complete 5-cycle |
 (the ones that are not green or orange in the table on the right) |
 This is the top left submatrix of all bigger tables of this kind (compare this one). |
 Here the blue patterns are not horizontally symmetric. |
Partitions
[edit | edit source]Infinite orderings of integer partitions and set partitions can be defined using CoLex ordering.
 The binary vectors are in CoLex order and correspond to the increasing sequence |
 The binary matrix in CoLex order is the top left corner of the right matrix in the box below. |
| Partitions of a 5-set | |
|---|---|
| The rows of the binary matrices are in CoLex order. (The white fields are 0s, colored fields are 1s. | |
 |
 |
Walsh functions
[edit | edit source]The rows of binary Walsh matrices in Lex and CoLex order give symmetric matrices.
For normal Walsh matrices (with 1 and −1 instead of 0 and 1) RevLex and RevCoLex would give this result.
 The arguments (read like binary vectors) are in Lex order. |
 |
 The arguments (r.l.b.v.) are in CoLex order. |
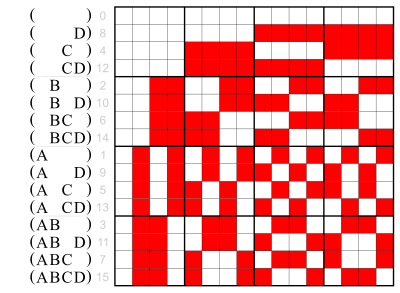
Subsets
[edit | edit source] |
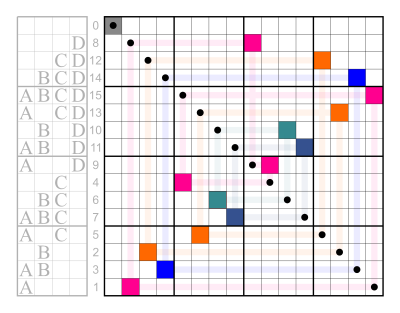 (This order does not seem to have a name.) |
The following Python code shows the 16 subsets of the set {a,b,c,d} in lexicographic order.
The second part shows that Lex order is the same as binary CoLex order, when the subsets themselves are reversed.
>>> asc = ['', 'a', 'b', 'ab', 'c', 'ac', 'bc', 'abc', 'd', 'ad', 'bd', 'abd', 'cd', 'acd', 'bcd', 'abcd']
>>> sorted(asc)
['', 'a', 'ab', 'abc', 'abcd', 'abd', 'ac', 'acd', 'ad', 'b', 'bc', 'bcd', 'bd', 'c', 'cd', 'd']
>>> desc = ['', 'a', 'b', 'ba', 'c', 'ca', 'cb', 'cba', 'd', 'da', 'db', 'dba', 'dc', 'dca', 'dcb', 'dcba']
>>> print desc == sorted(desc)
True
 also the Lex order of the reversed subsets |
 |
Hypercube faces
[edit | edit source]
The following lists show the vertices of the tesseracts k-faces for k in {3, 2, 1}.
(The tesseract is the 4-dimensional hypercube, and has 8 cubic cells, 24 square faces, 32 edges and 16 vertices.)
For the cubes Lex and CoLex are the same. The binary matrix on the right has rotational symmetry.
For squares and edges the two orderings are shown separately. Their binary matrices are rotations of each other.
| 8 cubes | ||
|---|---|---|
0 1 2 3 4 5 6 7 |
[ 0, 1, 2, 3, 4, 5, 6, 7], [ 0, 1, 2, 3, 8, 9, 10, 11], [ 0, 1, 4, 5, 8, 9, 12, 13], [ 0, 2, 4, 6, 8, 10, 12, 14], [ 1, 3, 5, 7, 9, 11, 13, 15], [ 2, 3, 6, 7, 10, 11, 14, 15], [ 4, 5, 6, 7, 12, 13, 14, 15], [ 8, 9, 10, 11, 12, 13, 14, 15] |
1111 1111 .... .... 1111 .... 1111 .... 11.. 11.. 11.. 11.. 1.1. 1.1. 1.1. 1.1. .1.1 .1.1 .1.1 .1.1 ..11 ..11 ..11 ..11 .... 1111 .... 1111 .... .... 1111 1111 |
| 24 squares | ||||||
|---|---|---|---|---|---|---|
| Lex | CoLex | |||||
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
[ 0, 1, 2, 3], [ 0, 1, 4, 5], [ 0, 1, 8, 9], [ 0, 2, 4, 6], [ 0, 2, 8, 10], [ 0, 4, 8, 12], [ 1, 3, 5, 7], [ 1, 3, 9, 11], [ 1, 5, 9, 13], [ 2, 3, 6, 7], [ 2, 3, 10, 11], [ 2, 6, 10, 14], [ 3, 7, 11, 15], [ 4, 5, 6, 7], [ 4, 5, 12, 13], [ 4, 6, 12, 14], [ 5, 7, 13, 15], [ 6, 7, 14, 15], [ 8, 9, 10, 11], [ 8, 9, 12, 13], [ 8, 10, 12, 14], [ 9, 11, 13, 15], [10, 11, 14, 15], [12, 13, 14, 15] |
1111 .... .... .... 11.. 11.. .... .... 11.. .... 11.. .... 1.1. 1.1. .... .... 1.1. .... 1.1. .... 1... 1... 1... 1... .1.1 .1.1 .... .... .1.1 .... .1.1 .... .1.. .1.. .1.. .1.. ..11 ..11 .... .... ..11 .... ..11 .... ..1. ..1. ..1. ..1. ...1 ...1 ...1 ...1 .... 1111 .... .... .... 11.. .... 11.. .... 1.1. .... 1.1. .... .1.1 .... .1.1 .... ..11 .... ..11 .... .... 1111 .... .... .... 11.. 11.. .... .... 1.1. 1.1. .... .... .1.1 .1.1 .... .... ..11 ..11 .... .... .... 1111 |
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
[ 0, 1, 2, 3], [ 0, 1, 4, 5], [ 0, 2, 4, 6], [ 1, 3, 5, 7], [ 2, 3, 6, 7], [ 4, 5, 6, 7], [ 0, 1, 8, 9], [ 0, 2, 8, 10], [ 1, 3, 9, 11], [ 2, 3, 10, 11], [ 8, 9, 10, 11], [ 0, 4, 8, 12], [ 1, 5, 9, 13], [ 4, 5, 12, 13], [ 8, 9, 12, 13], [ 2, 6, 10, 14], [ 4, 6, 12, 14], [ 8, 10, 12, 14], [ 3, 7, 11, 15], [ 5, 7, 13, 15], [ 9, 11, 13, 15], [ 6, 7, 14, 15], [10, 11, 14, 15], [12, 13, 14, 15] |
1111 .... .... .... 11.. 11.. .... .... 1.1. 1.1. .... .... .1.1 .1.1 .... .... ..11 ..11 .... .... .... 1111 .... .... 11.. .... 11.. .... 1.1. .... 1.1. .... .1.1 .... .1.1 .... ..11 .... ..11 .... .... .... 1111 .... 1... 1... 1... 1... .1.. .1.. .1.. .1.. .... 11.. .... 11.. .... .... 11.. 11.. ..1. ..1. ..1. ..1. .... 1.1. .... 1.1. .... .... 1.1. 1.1. ...1 ...1 ...1 ...1 .... .1.1 .... .1.1 .... .... .1.1 .1.1 .... ..11 .... ..11 .... .... ..11 ..11 .... .... .... 1111 | |
| 32 edges | ||||||
|---|---|---|---|---|---|---|
| Lex | CoLex | |||||
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
[ 0, 1], [ 0, 2], [ 0, 4], [ 0, 8], [ 1, 3], [ 1, 5], [ 1, 9], [ 2, 3], [ 2, 6], [ 2, 10], [ 3, 7], [ 3, 11], [ 4, 5], [ 4, 6], [ 4, 12], [ 5, 7], [ 5, 13], [ 6, 7], [ 6, 14], [ 7, 15], [ 8, 9], [ 8, 10], [ 8, 12], [ 9, 11], [ 9, 13], [10, 11], [10, 14], [11, 15], [12, 13], [12, 14], [13, 15], [14, 15] |
11.. .... .... .... 1.1. .... .... .... 1... 1... .... .... 1... .... 1... .... .1.1 .... .... .... .1.. .1.. .... .... .1.. .... .1.. .... ..11 .... .... .... ..1. ..1. .... .... ..1. .... ..1. .... ...1 ...1 .... .... ...1 .... ...1 .... .... 11.. .... .... .... 1.1. .... .... .... 1... .... 1... .... .1.1 .... .... .... .1.. .... .1.. .... ..11 .... .... .... ..1. .... ..1. .... ...1 .... ...1 .... .... 11.. .... .... .... 1.1. .... .... .... 1... 1... .... .... .1.1 .... .... .... .1.. .1.. .... .... ..11 .... .... .... ..1. ..1. .... .... ...1 ...1 .... .... .... 11.. .... .... .... 1.1. .... .... .... .1.1 .... .... .... ..11 |
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
[ 0, 1], [ 0, 2], [ 1, 3], [ 2, 3], [ 0, 4], [ 1, 5], [ 4, 5], [ 2, 6], [ 4, 6], [ 3, 7], [ 5, 7], [ 6, 7], [ 0, 8], [ 1, 9], [ 8, 9], [ 2, 10], [ 8, 10], [ 3, 11], [ 9, 11], [10, 11], [ 4, 12], [ 8, 12], [ 5, 13], [ 9, 13], [12, 13], [ 6, 14], [10, 14], [12, 14], [ 7, 15], [11, 15], [13, 15], [14, 15] |
11.. .... .... .... 1.1. .... .... .... .1.1 .... .... .... ..11 .... .... .... 1... 1... .... .... .1.. .1.. .... .... .... 11.. .... .... ..1. ..1. .... .... .... 1.1. .... .... ...1 ...1 .... .... .... .1.1 .... .... .... ..11 .... .... 1... .... 1... .... .1.. .... .1.. .... .... .... 11.. .... ..1. .... ..1. .... .... .... 1.1. .... ...1 .... ...1 .... .... .... .1.1 .... .... .... ..11 .... .... 1... .... 1... .... .... 1... 1... .... .1.. .... .1.. .... .... .1.. .1.. .... .... .... 11.. .... ..1. .... ..1. .... .... ..1. ..1. .... .... .... 1.1. .... ...1 .... ...1 .... .... ...1 ...1 .... .... .... .1.1 .... .... .... ..11 | |
As usual, the CoLex order is the one where the sequence for a lower dimension is the beginning of the sequence for a higher one.
The binary matrices shown above can be interpreted as integer sequences:
vertices: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768...
edges: 3, 5, 10, 12, 17, 34, 48, 68, 80, 136, 160, 192, 257, 514, 768, 1028, 1280, 2056, 2560, 3072, 4112, 4352, 8224, 8704, 12288, 16448, 17408, 20480, 32896, 34816, 40960, 49152...
squares: 15, 51, 85, 170, 204, 240, 771, 1285, 2570, 3084, 3840, 4369, 8738, 12336, 13056, 17476, 20560, 21760, 34952, 41120, 43520, 49344, 52224, 61440...
cubes: 255, 3855, 13107, 21845, 43690, 52428, 61680, 65280...
tesseracts: 65535...
Petrie polygon
[edit | edit source]A hypercube of dimension n has a Petrie polygon of size 2n, which is also the number of its facets. It passes the first half of them in ascending order, and the second half in descending order.
| Petrie polygons for n = 2..4 | |||||||
|---|---|---|---|---|---|---|---|

|

|

| |||||
| cube faces | |||||||
|---|---|---|---|---|---|---|---|
 0 |
 1 |
 2 |
 5 |
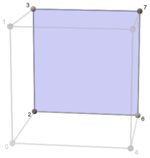 4 |
 3 | ||
| Each pair of consecutive edges belongs to one face. | |||||||
| tesseract cells | |||||||
|---|---|---|---|---|---|---|---|
 0 |
 1 |
 2 |
 3 |
 7 |
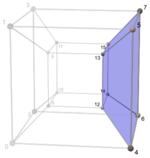 6 |
 5 |
 4 |
| Each triple of consecutive edges belongs to one cell. | |||||||


















