Walsh permutation
The term n-bit Walsh permutation was chosen by the author for permutations of 2n elements, that permute Walsh functions into other Walsh functions.
Walsh permutations of 2n elements can be represented by an n-element compression vector
of integers referring to the numbering of Walsh functions (displayed in orange in the images).
It corresponds to the n×n compression matrix. It's columns show the elements of the compression vector in binary representation.
The multiplication of the compression matrices (with F2 operations) corresponds to the composition of the permutations.
As the compression matrices are the elements of the general linear group GL(n,2) the Walsh permutations form a group isomorphic to GL(n,2).
There are ![]() A002884(n) n-bit Walsh permutations.
A002884(n) n-bit Walsh permutations.

(the product of two Walsh permutations related to bent functions)

Not all vectors with different elements correspond to Walsh permutations, as the following example shows:
| No Walsh permutation wp(1,2,3,4) | ||
|---|---|---|
|
Notation warning[edit | edit source]
This article and its subpages currently use two different ways to name and display Walsh permutations. In older files the direction of the compression vector is horizontal, and the permutation is vertical. In new files both compression vector and permutation are horizontal. The old files are gradually replaced. 3-bit Walsh permutation already uses new files.
 = wp(7, 2, 4) old |
 new: horizontal (0, 1, 3, 2, 5, 4, 6, 7) old: vertical (0, 7, 2, 5, 4, 3, 6, 1) |
 = wp(1, 2, 6, 10) new |
 Bit permutation[edit | edit source]
Bit permutation[edit | edit source]

When a simple permutation of n elements is applied on the binary digits of numbers from 0 to 2n-1 the result is a permutation of the numbers from 0 to 2n-1.
The example on the right corresponds to the simple permutation that swaps the first two and the last two digits of the 4-bit binary numbers.
Probably the most important bit permutation is the bit-reversal permutation.
 Nimber multiplication[edit | edit source]
Nimber multiplication[edit | edit source]

The rows of each nimber multiplication table are Walsh permutations (except row 0).
They are not only closed under multiplication (function composition), but even under addition (bitwise XOR).
 Gray code permutation powers[edit | edit source]
Gray code permutation powers[edit | edit source]

Powers of the Gray code permutation have very simple compression matrices and vectors.
In each vector all entries follow from the first one, and the first entries follow from the rows of the Sierpinski triangle.
See also Algebraic normal form.
 Sequency ordered Walsh matrix[edit | edit source]
Sequency ordered Walsh matrix[edit | edit source]

The permutation that changes the natural ordered into the sequency ordered Walsh matrix is the product of the Gray code permutation and the bit-reversal permutation.
 Bent functions[edit | edit source]
Bent functions[edit | edit source]

Each bent function corresponds to a Walsh permutation.
This can be seen when all rows of its sec matrix are XORed with the function itself (second step in the example on the right).
 Magic squares[edit | edit source]
Magic squares[edit | edit source]
 These matrices are found in the dual matrices of the magic squares. |
 |
There are 24*9=216 Walsh permutations that correspond to magic squares of order 4.
One my say that only 6 of them are essentially different.
 Inversions[edit | edit source]
Inversions[edit | edit source]
 |
 |
 |
Some inversion sets of Walsh permutations are very regular.
E.g. there are 2n-1 n-bit Walsh permutations with horizontally striped inversion sets (like the left one of the examples).
The pattern of the stripes is that of Walsh functions.
 2-bit[edit | edit source]
2-bit[edit | edit source]
The ![]() A002884(2) = 6 2-bit Walsh permutations form general linear group GL(2,2), which is also the symmetric group S3.
A002884(2) = 6 2-bit Walsh permutations form general linear group GL(2,2), which is also the symmetric group S3.
 3-bit[edit | edit source]
3-bit[edit | edit source]
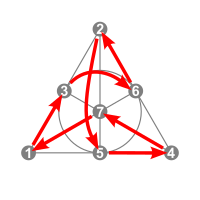
The ![]() A002884(3) = 168 3-bit Walsh permutations correspond to the collineations of the Fano plane.
A002884(3) = 168 3-bit Walsh permutations correspond to the collineations of the Fano plane.
Compression vectors, Permutations
4-bit[edit | edit source]
There are ![]() A002884(4) = 20160 4-bit Walsh permutations.
A002884(4) = 20160 4-bit Walsh permutations.
Fixed points[edit | edit source]
The fixed points of an n-bit Walsh permutation are seals of arity n.
1001 1001 (compare matrix 12 in this list)