OpenStax University Physics/E&M/Magnetic Forces and Fields

${\mathcal {E}}\&{\mathcal {M}}$ (Vol. 2):    5:Electric Charges and Fields    6:Gauss's Law    7:Electric Potential    8:Capacitance    9:Current and Resistance    10:Direct-Current Circuits    11:Magnetic Forces and Fields    12:Sources of Magnetic Fields    13:Electromagnetic Induction    14:Inductance    15:Alternating-Current Circuits    16:Electromagnetic Waves

Subpages

Chapter 11

Magnetic Forces and Fields

• 
  Cross product $|{\vec {a}}\times {\vec {b}}|$$=ab\sin \theta$
• 
  Hall effect ${\vec {v}}_{d}={\vec {E}}\times {\vec {B}}/B^{2}$
• 
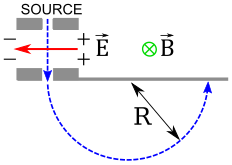
  Mass spectrometer in special case that both magnetic fields are equal

▭ ${\vec {F}}=q{\vec {v}}\times {\vec {B}}$ is the force due to a magnetic field on a moving charge.
▭ For a current element oriented along ${\overrightarrow {d\ell }},\;d{\vec {F}}=I{\overrightarrow {d\ell }}\times {\vec {B}}$.

▭ The SI unit for magnetic field is the Tesla: 1T=10⁴ Gauss.
▭ Gyroradius $r={\tfrac {mB}{qB}}.\;$ Period $T={\tfrac {2\pi m}{qB}}.\;$
▭ Torque on current loop ${\vec {\tau }}={\vec {\mu }}\times {\vec {B}}$ where ${\vec {\mu }}=NIA{\hat {n}}$ is the dipole moment. Stored energy $U={\vec {\mu }}\cdot {\vec {B}}.$
▭ Drift velocity in crossed electric and magnetic fields $v_{d}={\tfrac {E}{B}}$
▭ Hall voltage = $V$ where the electric field is $E=V/\ell =Bv_{d}={\tfrac {IB}{neA}}$
▭ Charge-to-mass ratio $q/m={\tfrac {E}{BB_{0}r}}$ where the $E$ and $B$ fields are crossed and $E=0$ when the magnetic field is $B_{0}$

For quiz at QB/d_cp2.11

cross product

$|{\vec {a}}\times {\vec {b}}|$$=ab\sin \theta \Leftrightarrow$ $({\vec {a}}\times {\vec {b}})_{x}=(a_{y}b_{z}-a_{z}b_{y})$, $({\vec {a}}\times {\vec {b}})_{y}=(a_{z}b_{x}-a_{x}b_{z})$, $({\vec {a}}\times {\vec {b}})_{z}=(a_{x}b_{y}-a_{y}b_{x})$
Magnetic force: ${\vec {F}}=q{\vec {v}}\times {\vec {B}},\;$$d{\vec {F}}=I{\overrightarrow {d\ell }}\times {\vec {B}}$.
${\vec {v}}_{d}={\vec {E}}\times {\vec {B}}/B^{2}$=EXB drift velocity
Circular motion (uniform B field): $r={\tfrac {mv}{qB}}.\;$ Period=$T={\tfrac {2\pi m}{qB}}.\;$

Hall effect

Dipole moment=${\vec {\mu }}=NIA{\hat {n}}$. Torque=${\vec {\tau }}={\vec {\mu }}\times {\vec {B}}$. Stored energy=$U={\vec {\mu }}\cdot {\vec {B}}$.
Hall field =$E=V/\ell =Bv_{d}={\tfrac {IB}{neA}}$
Lorentz force =$q\left({\vec {E}}+{\vec {v}}\times {\vec {B}}\right)$