OpenStax University Physics/E&M/Electric Charges and Fields

${\mathcal {E}}\&{\mathcal {M}}$ (Vol. 2):    5:Electric Charges and Fields    6:Gauss's Law    7:Electric Potential    8:Capacitance    9:Current and Resistance    10:Direct-Current Circuits    11:Magnetic Forces and Fields    12:Sources of Magnetic Fields    13:Electromagnetic Induction    14:Inductance    15:Alternating-Current Circuits    16:Electromagnetic Waves

Subpages

Chapter 5

Electric Charges and Fields

Coulomb's Law ${\vec {F}}={\tfrac {1}{4\pi \varepsilon _{0}}}{\tfrac {q_{1}q_{2}}{r_{12}^{2}}}{\hat {r}}_{12}$ where the vacuum permittivity $\varepsilon _{0}=$ 8.85×10⁻¹² F/m.

Elementary charge = e = 1.602×10⁻¹⁹C (electrons have charge q=−e and protons have charge q=+e.)

Dipole moment

▭ By superposition, ${\vec {F}}={\tfrac {1}{4\pi \varepsilon _{0}}}Q\sum _{i=1}^{N}{\tfrac {q_{i}}{r_{Qi}^{2}}}{\hat {r}}_{Qi}$ where ${\vec {r}}_{Qi}={\vec {r}}_{Q}-{\vec {r}}_{i}$
▭ Electric field ${\vec {F}}=Q{\vec {E}}$ where ${\vec {E}}({\vec {r}}_{P})={\tfrac {1}{4\pi \varepsilon _{0}}}\sum _{i=1}^{N}{\tfrac {q_{i}}{r_{Pi}^{2}}}{\hat {r}}_{Pi}$ is the field at ${\vec {r}}_{P}$ due to charges at ${\vec {r}}_{i}$
▭ The field above an infinite wire ${\vec {E}}(z)={\tfrac {1}{4\pi \varepsilon _{0}}}{\tfrac {2\lambda }{z}}{\hat {k}}$ and above an infinite plane ${\vec {E}}={\tfrac {\sigma }{2\varepsilon _{0}}}{\hat {k}}$
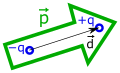
▭ An electric dipole ${\vec {p}}=q{\vec {d}}$ in a uniform electric field experiences the torque $\tau ={\vec {p}}\times {\vec {E}}$

For quiz at QB/d_cp2.5

$\varepsilon _{0}=$ 8.85×10⁻¹² F/m = vacuum permittivity.

e = 1.602×10⁻¹⁹C: negative (positive) charge for electrons (protons)

$k_{e}={\tfrac {1}{4\pi \varepsilon _{0}}}=$ = 8.99×10⁹ m/F

${\vec {F}}=Q{\vec {E}}$ where ${\vec {E}}={\tfrac {1}{4\pi \varepsilon _{0}}}\sum _{i=1}^{N}{\tfrac {q_{i}}{r_{Pi}^{2}}}{\hat {r}}_{Pi}$

${\vec {E}}=\int {{\tfrac {dq}{{r}^{2}}}{\hat {r}}}$ where $dq=\lambda d\ell =\sigma da=\rho dV$

$E={\tfrac {\sigma }{2\varepsilon _{0}}}$ = field above an infinite plane of charge.