MyOpenMath/Three types of test questions

Abstract:Of the three kinds of questions, only one needs to be finished.
Outline: 1. Reform: Two tasks for the reformer: first convince people the reform is needed, second lay out a plan. 2. Type 1-2 errors. 3. sss
- open educational resources wikiversity link
- The advantages of assessing students before the course begins cannot be overstated. Mechanisms already exist that allow students to skip a required course,[1] and the introduction of quasi-standardized[2] undergraduate prelims will facilitate further evolution of such alternative assessments.[3]I am confident that all the flaws associated with an initial effort to create an open source exam bank for undergraduate prelims can be overcome by providing students with alternative assessments.
Three types of test questions
[edit | edit source]Of the three kinds of test questions on a first effort to create our bank, current efforts should focus on the third:
- Simple fact-based knowledge questions.
- Traditional "problems"[4] that require a calculation.
- Reading comprehension with fact-based follow-up questions.
The first two types actually represent the ends of a continuous spectrum. To some extent, the student's solution to any question requiring a calculation is based on the student's ability to remember the solution to another problem. With the ever-increasing practice of Google-solving, one can argue that the traditional exercise of using thought to solve a physics problem no longer exists.
- Concept inventory questions. If the circumstances are favorable, these questions effectively measure a student's grasp of fundamental ideas.[5] Unfortunately, the release of any quizbank information to students is essentially "teaching-to-the-test", and therefore diametrically opposite to any authentic assessment. Ways to compensate for the absence of such questions shall be discussed below.
- Essay questions and oral exams. These are by far the most effective assessments if the goal is to permit students to bypass a prerequisite course. I view such essays and oral exams as an opportunity to compensate for the obvious flaws associated attempting to design a collection of undergraduate prelims for introductory college courses.
Two short "essays" with sample questions
[edit | edit source]key points to mention here or elsewhere
- True false questions
- Disjoint nature of the two essays
- Important to introduce all formulas in review
- Reviewing material is permissible b/c it teaches students to skim.
- Short essays and TF will permit students to contribute to the bank
- Plan is to start "low-tech" and hope "high-tech" versions follow
Review of binomial coefficients
[edit | edit source]The binomial coefficient, is often pronounced as "n choose k":
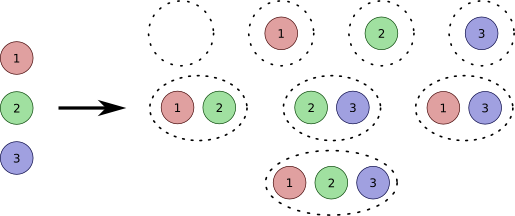
where the factorial is expressed as While this "definition" leads naturally to , it does little to justify the empty product convention,[6] which is that This convention also supports An examination of 3 choose k for k also supports the use of this convention[7] for both and as shown to the left in the figure below:
In this figure, the three objects are the colored circles, labeled 1,2,3.[8] On the right, we see that 3 choose 2 and 3 choose 1 are equal.
The other pair of binomial coefficients shown in the figure above are obviously equal: When choosing from 3 items, selecting two items is equivalent to not selecting one item. Instead of "choosing" either one or two items, both coefficients represent splitting the items into two groups: One group contains 1 item, while the other contains 2 items.
When introducing binomial coefficients to students for the first time, this example can be used to establish that the order in which objects are chosen has no significance. The above figure makes it abundantly clear that the choice 1,2 is equivalent the choice 2,1.
Number of words that can be created from a set of letters
[edit | edit source]
Here we use properties of the binomial coefficient to solve a more complex problem. Consider the set of positive integers less than or equal to eleven: {1,2,3,...11}. While the binomial coefficients permit us to group the elements of this set into two distinct sets, we now seek to group the eleven members of this set into four groups. For reasons that will become clear, we label these four sets with the capital letters: I, M, P, S. The eleven integers shall be placed into these groups (or "bins") in the following manner:
- 4 elements are placed in bin I
- 1 element is placed in bin M
- 2 elements are placed in bin P
- 4 elements are placed in bin S
For example, the number of distinct permutations of the letters of the word MISSISSIPPI, which has 1 M, 4 Is, 4 Ss, and 2 Ps, is
Educational "reform": easier said than done
[edit | edit source]private and public institutions
competing interests and vaguely defined division of power
perestroika driving on left to right
I have hope for this
Type-1 and type-2 assessment errors
[edit | edit source]The construction of a publicly available OER bank questions preliminary exams in STEM courses is greatly simplified by a surprising fact: There is little need for concern ???about the quality of the questions. This can be explained in the language of hypothesis testing, taking the null hypotheses to be that the student is prepared to skip a portion of the course.[9].
There is almost no reason to be concerned??? about a type-1 error, where a qualified student fails the prelim an is told to take the course. Keep in mind that student has studied a topic before taking a course, at zero financial cost. Perhaps the student will learn how not to learn a topic. Perhaps the student will uncover (or document) a test-taking disability. Perhaps the student has exposed a flaw in the test that the college needs to know about. All of these type-1 errors uncover issues that need to be resolved as soon as possible. Keep in mind that the alternative to learning about these issues before a student enrolls in a course is for them to be discovered after time and money has been wasted on an unsuccessful effort to complete a college course.
A simple remedy for the type-1 error is to provide alternative assessments to students who fail the prelim but continue to believe they know the perquisite material. MENTION THE OPTIONS
A path through the wilderness
[edit | edit source]Temporary odds and ends to be included/discarded
[edit | edit source]This proof reminded me of the fact that I have been contemplating the problem of writing test questions specifically designed for an open source quizbank.
How_things_work_college_course/Conceptual_physics_wikiquizzes/Velocity_and_acceleration
- ↑ After getting my undergraduate degree in physics, I spent two gap years studying graduate level physics, while working part time at an IHOP. I was scheduled to take a three-semester course that covered Jackson's Electrodynamics. Upon my request to skip the course, the professor opened the book to a random page. I knew enough from the top of my head about spherical harmonics to bypass the entire sequence.
- ↑ I all them "quazi-standardized" for two reasons: (1) there will be no strictly enforced uniform standards
- ↑ For example, contribution to these undergraduate prelim exams could serve as an alternative assessment for those with test anxiety, dyslexia, or other neurological conditions
- ↑ I place "problems" in quotation marks because the majority of such entities are pedagogical in nature and at best marginally related to real-life situations. No criticism of higher education is intended here; the complexity of the "real world" is such that our goal is not to
- ↑ My experience is with w:Force Concept Inventory
- ↑ Perhaps the most well-known argument that should equal unity involves the gamma function.
- ↑ In set theory means that is in the set
- ↑ One might be able to argue that the convention that there is one way to select zero objects is arbitrary by saying that it is meaningless to count the ways to do nothing. On the other hand, a strong case can be made there is one way to select all three items. Both formulas involve 0!.
- ↑ If the test exempts students from the first of multi-course series, most colleges would probably require that the student either take the next course, or successfully engage in a follow-up workshop or seminar on the subject. The simplest such followup would be to require attendance and some sort of performance in the last weeks of the course that the student wishes to test out of.