MyOpenMath/Solutions/Electric Flux
Portions of this page are under a CC BY-NC-SA copyright from Rice University that can be downloaded for free at http://cnx.org/content/col12074/latest/
1

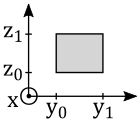
Each surface of the rectangular box shown is aligned with the xyz coordinate system. Two surfaces occupy identical rectangles in the planes x=0 and x=x1=3 m. The other four surfaces are rectangles in y=y0=1 m, y=y1=5 m, z=z0=1 m, and z=z1=3 m. The surfaces in the yz plane each have area 8m2. Those in the xy plane have area 12m2 ,and those in the zx plane have area 6m2. An electric field of magnitude 10 N/C has components in the y and z directions and is directed at 30° above the xy-plane (i.e. above the y axis.) What is the magnitude (absolute value) of the electric flux through a surface aligned parallel to the xz plane?[1]
- Solution: Φ=5.196E+01 N·m2/C. The face is marked at the bottom of the square, and the angle of the electric field is shown as θ In this case, the flux is (10 N/C)(6m2)(cos30°)=51.96 Nm2/C
2

Each surface of the rectangular box shown is aligned with the xyz coordinate system. Two surfaces occupy identical rectangles in the planes x=0 and x=x1=3 m. The other four surfaces are rectangles in y=y0=1 m, y=y1=5 m, z=z0=1 m, and z=z1=3 m. The surfaces in the yz plane each have area 8m2. Those in the xy plane have area 12m2 ,and those in the zx plane have area 6m2. An electric field of magnitude 10 N/C has components in the y and z directions and is directed at 60° from the z-axis. What is the magnitude (absolute value) of the electric flux through a surface aligned parallel to the xz plane? [2]
- Solution: Φ=5.196E+01 N·m2/CThis is like the previous problem, except now the angle is measured with respect to the z axis so we instead use sin60° and get the same answer: (10 N/C)(6m2)(sin60°)=51.96 Nm2/C
3

Each surface of the rectangular box shown is aligned with the xyz coordinate system. Two surfaces occupy identical rectangles in the planes x=0 and x=x1=3 m. The other four surfaces are rectangles in y=y0=1 m, y=y1=5 m, z=z0=1 m, and z=z1=3 m. The surfaces in the yz plane each have area 8m2. Those in the xy plane have area 12m2 ,and those in the zx plane have area 6m2. An electric field has the xyz components (0, 8.7, 5.0) N/C. What is the magnitude (absolute value) of the electric flux through a surface aligned parallel to the xz plane?[3]
- Solution This is the same geometry, except now we take only the y-component: Φ=(8.7N/C)(6m2)=52.2 Nm2/C
4
What is the magnetude (absolute value) of the electric flux through a rectangle that occupies the z=0 plane with corners at (x,y)= (x=0, y=0), (x=3, y=0), (x=0, y=2), and (x=3, y=2), where x and y are measured in meters. The electric field is
- Solution: The dimensions of the rectangle are , where and . We only care about the z component of the electric field. Instead of being the flux, we have to break the rectangle up into little rectangles, each with area , where is very small:
- = 24 (units are either V·m or N·m2/C)
5

Five concentric spherical shells have radius of exactly (1m, 2m, 3m, 4m, 5m).Each is uniformly charged with 5 nano-Coulombs. What is the magnitude of the electric field at a distance of 3.5 m from the center of the shells?[4]
- Solution: By Gauss's law the charge enclosed by a sphere of radius 3.5 meters is determined by the fact that charged spheres have radius less than 2.5 meters:
- Spherical symmetry (or more precisely spherical invariance) renders the surface integral trivial:
- ,
- where . Equating this integral to yields the desired result: 1.102E+01 N/C.
6
A non-conducting sphere of radius R=2 m has a non-uniform charge density that varies with the distnce from its center as given by ρ(r)=ar2 (r≤R) where a=1 nC·m-1. What is the magnitude of the electric field at a distance of 1 m from the center?[5]
- Solution: Here, , is the easy integral in Gauss's law. The difficult integral is finding the enclosed charge:
- Here, is one of many notations used to denote a small volume differential (other notations being ) For our purposes, we can use symmetry to divide our sphere into small shells of volume,
- Since the variable has already been taken to denote the radius of the Gaussian sphere, we make a "change of variables",
- (using .)
- Hence the charge enclosed by a sphere of radius r is:
- I think this yeilds = 2.259E+01 N/C
OER Attribution
- ↑ Inspired by Example 6.3 from OpenStax University Physics2: https://cnx.org/contents/eg-XcBxE@9.8:7Rx6Svvy@4/61-Electric-Flux_1
- ↑ Example 6.3a from OpenStax University Physics2: https://cnx.org/contents/eg-XcBxE@9.8:7Rx6Svvy@4/61-Electric-Flux_1
- ↑ Example 6.3b from OpenStax University Physics2: https://cnx.org/contents/eg-XcBxE@9.8:7Rx6Svvy@4/61-Electric-Flux_1
- ↑ Inspired by Example 6.6 from OpenStax University Physics2, but modified by user:Guy vandegrift.
- ↑ Example 6.7 from OpenStax University Physics2: https://cnx.org/contents/eg-XcBxE@9.8:7NEpGtkt@4/63-Applying-Gausss-Law_1

























