Inverse limit
Wiki2Reveal Slide for Inverse Limit
[edit | edit source]This page can be displayed as Wiki2Reveal slides. Single sections are regarded as slides and modifications on the slides will immediately affect the content of the slides (see Wiki2Reveal for further details or Lecture aboout Inverse Producing Algebra Extensions (german) if you want to create a course page with Wiki2Reveal for a lecture)
Introduction
[edit | edit source]In mathematics, the inverse limit (also called the projective limit) is a construction that allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects. Inverse limits can be defined in any category, and they are a special case of the concept of a limit in category theory.
Objective
[edit | edit source]This learning resource in Wikiversity has the objective to provide a Wiki2Reveal environment for lectures and seminars about Algebra. The presentation can be used in lectures to explain the topic and the lecturer can annotate the slides with a stylus in the browsers or students can use the slides in seminars to explain the topic of inverse limits.
Target Group
[edit | edit source]The target group of the learning resource are students and lectures in Mathematics that want present or explain the concept of inverse limits an annotate the slides in the browser. Press F for Fullscreen and C to mark certain areas on the slides.
Formal definition
[edit | edit source]The formal definition consists of the following steps:
- Definition of the inverse system that creates mappings between groups
- the mappings are homomorphisms between the groups
Family of Groups
[edit | edit source]We start with the definition of an inverse system (or projective system) of groups and homomorphisms. Let (, ≤) be a directed poset (not all authors require I to be directed). Let (Ai)i∈I be a family of groups.
Family of Group Homomorphisms
[edit | edit source]Suppose we have a family of homomorphisms for all (note the order) with the following properties:
- is the identity on ,
Then the pair is called an inverse system of groups and morphisms over , and the morphisms are called the transition morphisms of the system.
Inverse System and Inverse Limit
[edit | edit source]We define the inverse limit of the inverse system as a particular subgroup of the direct product of the 's:
Remark
[edit | edit source]The inverse limit comes equipped with natural projections >: → which pick out the ith component of the direct product for each in . The inverse limit and the natural projections satisfy a universal property described in the next section.
This same construction may be carried out if the 's are sets,[1] semigroups,[1] topological spaces,[1] rings, modules (over a fixed ring), algebras (over a fixed ring), etc., and the homomorphisms are morphisms in the corresponding category. The inverse limit will also belong to that category.
General definition
[edit | edit source]The inverse limit can be defined abstractly in an arbitrary category by means of a universal property. Let be an inverse system of objects and morphisms in a category C (same definition as above). The inverse limit of this system is an object X in C together with morphisms i: X → Xi (called projections) satisfying i = ∘ j for all i ≤ j.
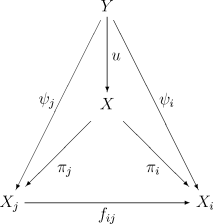
Diagram
[edit | edit source]The pair (X, i) must be universal in the sense that for any other such pair (Y, ψi) there exists a unique morphism u: Y → X such that the diagram
commutes for all i ≤ j. The inverse limit is often denoted
with the inverse system being understood.
Existence and Uniqueness of Inverse Systems
[edit | edit source]In some categories, the inverse limit of certain inverse systems does not exist. If it does, however, it is unique in a strong sense: given any two inverse limits and of an inverse system, there exists a unique isomorphism commuting with the projection maps.
Category C and partially ordered sets
[edit | edit source]Inverse systems and inverse limits in a category C admit an alternative description in terms of functors. Any partially ordered set I can be considered as a small category where the morphisms consist of arrows i → j if and only if i ≤ j. An inverse system is then just a contravariant functor I → C. Let be the category of these functors (with natural transformations as morphisms). An object X of C can be considered a trivial inverse system, where all objects are equal to X and all arrow are the identity of X. This defines a "trivial functor" from C to The direct limit, if it exists, is defined as a right adjoint of this trivial functor.
Examples
[edit | edit source]The following list provides examples of inverse limits
Example 1 - p-adic Integers
[edit | edit source]The ring of p-adic integers is the inverse limit of the rings (see modular arithmetic) with the index set being the natural numbers with the usual order, and the morphisms being "take remainder". That is, one considers sequences of integers such that each element of the sequence "projects" down to the previous ones, namely, that whenever The natural topology on the p-adic integers is the one implied here, namely the product topology with cylinder sets as the open sets.
Example 2 - p-adic Solenoids
[edit | edit source]The ring of p-adic solenoids is the inverse limit of the rings (see modular arithmetic) with the index set being the natural numbers with the usual order, and the morphisms being "take remainder". That is, one considers sequences of real numbers such that each element of the sequence "projects" down to the previous ones, namely, that whenever
Example 3 - Factor Groups
[edit | edit source]Let p be a prime number. Consider the direct system composed of the factor groups and the homomorphisms induced by multiplication by . The inverse limit of this system is the circle group , expressed in a positional number system of base . This is similar to the construction of the real numbers by Cauchy sequences, using elements of the Prüfer group instead of the rational numbers or base decimal fractions.
Example 4 - Formal Power Series
[edit | edit source]The ring of formal power series over a commutative ring R can be thought of as the inverse limit of the rings , indexed by the natural numbers as usually ordered, with the morphisms from to given by the natural projection.
Example 5 - Pro-finite Groups
[edit | edit source]Pro-finite groups are defined as inverse limits of (discrete) finite groups.
Example 6 - Natural Projections
[edit | edit source]Let the index set I of an inverse system (Xi, ) have a greatest element m. Then the natural projection m: X → Xm is an isomorphism.
Example 7 - Inverse system and inverse limits - Category Sets
[edit | edit source]In the category of sets, every inverse system has an inverse limit, which can be constructed in an elementary manner as a subset of the product of the sets forming the inverse system. The inverse limit of any inverse system of non-empty finite sets is non-empty. This is a generalization of Kőnig's lemma in graph theory and may be proved with Tychonoff's theorem, viewing the finite sets as compact discrete spaces, and then applying the finite intersection property characterization of compactness.
Example 8 - Topological Spaces
[edit | edit source]In the category of topological spaces, every inverse system has an inverse limit. It is constructed by placing the initial topology on the underlying set-theoretic inverse limit. This is known as the limit topology.
Example 9 - Set of Strings in Computer Science
[edit | edit source]The set of infinite strings is the inverse limit of the set of finite strings, and is thus endowed with the limit topology. As the original spaces are discrete, the limit space is totally disconnected. This is one way of realizing the p-adic numbers and the Cantor set (as infinite strings).
Derived functors of the inverse limit
[edit | edit source]For an abelian category C, the inverse limit functor
is left exact.
Ordered and Countable
[edit | edit source]If I is ordered (not simply partially ordered) and countable, and C is the category Ab of abelian groups, the Mittag-Leffler condition is a condition on the transition morphisms fij that ensures the exactness of . Specifically, Eilenberg constructed a functor
(pronounced "lim one") such that if (Ai, fij), (Bi, gij), and (Ci, hij) are three inverse systems of abelian groups, and
is a short exact sequence of inverse systems, then
is an exact sequence in Ab.
Mittag-Leffler condition
[edit | edit source]If the ranges of the morphisms of an inverse system of abelian groups (Ai, fij) are stationary, that is, for every k there exists j ≥ k such that for all i ≥ j : one says that the system satisfies the Mittag-Leffler condition.
Origine of the Name
[edit | edit source]The name "Mittag-Leffler" for this condition was given by Bourbaki in their chapter on uniform structures for a similar result about inverse limits of complete Hausdorff uniform spaces. Mittag-Leffler used a similar argument in the proof of Mittag-Leffler's theorem.
Examples for Mittag-Leffler condition
[edit | edit source]The following situations are examples where the Mittag-Leffler condition is satisfied:
- a system in which the morphisms fij are surjective
- a system of finite-dimensional vector spaces or finite abelian groups or modules of finite length or Artinian modules.
An example where is non-zero is obtained by taking I to be the non-negative integers, letting Ai = piZ, Bi = Z, and Ci = Bi / Ai = Z/piZ. Then
where Zp denotes the p-adic integers.
Further results
[edit | edit source]More generally, if C is an arbitrary abelian category that has enough injectives, then so does CI, and the right derived functors of the inverse limit functor can thus be defined. The nth right derived functor is denoted
In the case where C satisfies Grothendieck's axiom (AB4*), Jan-Erik Roos generalized the functor lim1 on AbI to series of functors limn such that
It was thought for almost 40 years that Roos had proved (in Sur les foncteurs dérivés de lim. Applications. ) that lim1 Ai = 0 for (Ai, fij) an inverse system with surjective transition morphisms and I the set of non-negative integers (such inverse systems are often called "Mittag-Leffler sequences"). However, in 2002, Amnon Neeman and Pierre Deligne constructed an example of such a system in a category satisfying (AB4) (in addition to (AB4*)) with lim1 Ai ≠ 0. Roos has since shown (in "Derived functors of inverse limits revisited") that his result is correct if C has a set of generators (in addition to satisfying (AB3) and (AB4*)).
Barry Mitchell has shown (in "The cohomological dimension of a directed set") that if I has cardinality (the dth infinite cardinal), then Rnlim is zero for all n ≥ d + 2. This applies to the I-indexed diagrams in the category of R-modules, with R a commutative ring; it is not necessarily true in an arbitrary abelian category (see Roos' "Derived functors of inverse limits revisited" for examples of abelian categories in which limn, on diagrams indexed by a countable set, is nonzero for n > 1).
Related concepts and generalizations
[edit | edit source]The categorical dual of an inverse limit is a direct limit (or inductive limit). More general concepts are the limits and colimits of category theory. The terminology is somewhat confusing: inverse limits are a class of limits, while direct limits are a class of colimits.
Learning Tasks / Activities
[edit | edit source]- Explain how the ordered sets in is linked to properties of the group homomorphisms.
See also
[edit | edit source]Notes
[edit | edit source]- ↑ 1.0 1.1 1.2 John Rhodes & Benjamin Steinberg. The q-theory of Finite Semigroups. p. 133. ISBN 978-0-387-09780-0.
References
[edit | edit source]- Bourbaki, Nicolas (1989), Algebra I, Springer, ISBN 978-3-540-64243-5, OCLC 40551484
{{citation}}: Check|authorlink=value (help) - Bourbaki, Nicolas (1989), General topology: Chapters 1-4, Springer, ISBN 978-3-540-64241-1, OCLC 40551485
{{citation}}: Check|authorlink=value (help) - Mac Lane, Saunders (September 1998), Categories for the Working Mathematician (2nd ed.), Springer, ISBN 0-387-98403-8
{{citation}}: Check|authorlink=value (help) - Mitchell, Barry (1972), "Rings with several objects", Advances in Mathematics - MR 0294454, 8: 1–161, doi:10.1016/0001-8708(72)90002-3
{{citation}}: Check|author-link=value (help) - Neeman, Amnon (2002), "A counterexample to a 1961 "theorem" in homological algebra (with appendix by Pierre Deligne)", Inventiones Mathematicae MR: 1906154, 148 (2): 397–420, doi:10.1007/s002220100197
{{citation}}: Check|author-link=value (help) - Roos, Jan-Erik (1961), "Sur les foncteurs dérivés de lim. Applications", C. R. Acad. Sci. Paris MR: 0132091, 252: 3702–3704
{{citation}}: Check|author-link=value (help) - Roos, Jan-Erik (2006), "Derived functors of inverse limits revisited", J. London Math. Soc., Series 2 - MR 2197371, 73 (1): 65–83, doi:10.1112/S0024610705022416
{{citation}}: Check|author-link=value (help)
Page Information
[edit | edit source]You can display this page as Wiki2Reveal slides
Wiki2Reveal
[edit | edit source]The Wiki2Reveal slides were created for the Algebra Course - Slides' and the Link for the Wiki2Reveal Slides was created with the link generator.
- This page is designed as a PanDocElectron-SLIDE document type.
- Source: Wikiversity https://en.wikiversity.org/wiki/Inverse%20limit
- see Wiki2Reveal for the functionality of Wiki2Reveal.
Wikipedia2Wikiversity
[edit | edit source]This page was based on the following Wikipedia source page:





























![{\displaystyle R[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97ef3abdc745032b4d0ff06ee85ee220b1978da7)
![{\displaystyle \textstyle R[t]/t^{n}R[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80cc9becb0021ee974d04ada52fd76e5c38effaf)
![{\displaystyle \textstyle R[t]/t^{n+j}R[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/244af7ecce917c226dca459f261ee57b7a89ada7)










