Introduction to Cartesian Geometry
Welcome to Introduction to Cartesian Geometry
In Cartesian or Analytic Geometry we will learn how to represent points, lines, and planes using the Cartesian Coordinate System, also called Rectangular Coordinate System. This can be applied to solve a broad range of problems from geometry to algebra and it will be very useful later on Calculus.
Cartesian Coordinate System
[edit | edit source]The foundations of Analytic Geometry lie in the search for describing geometric shapes by using algebraic equations. One of the most important mathematicians that helped to accomplish this task was René Descartes for whom the name is given to this exciting subject of mathematics.
The Coordinate System
[edit | edit source]For a coordinate system to be useful we want to give to each point an attribute that helps to distinguish and relate different points. In the Cartesian system we do that by describing a point using the intersection of two(2D Coordinates) or more(Higher Dimensional Coordinates) lines. Therefore a point is represented as P(x1,x2,x3,...,xn) in "n" dimensions.
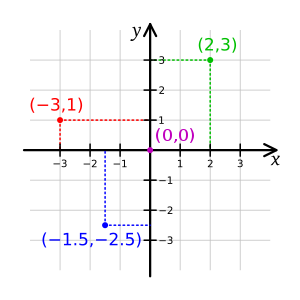
2D Coordinates
[edit | edit source]You can look at a 2D Coordinate system as a system in which a point can be defined using two values. We do this by using two perpendicular and directed lines called the abscissa(x-axis) and the ordinate(y-axis). The point of intersection of these two lines is called the origin denoted O(0,0). Any point can be determined as P(x,y), where x is the value in the x-axis and y is the value in the y-axis.
3d Coordinate Geometry
[edit | edit source]The coordinate system in two dimensions uses values containing width and depth expressed as values of and/or
Coordinate geometry in three dimensions adds the dimension of height, usually expressed as a value of The axes of and usually represent the horizontal plane. The axis is thus vertical or normal to the plane of and
In three dimensional space a point is shown as where the 3 values locate the point relative to the origin along each of the axes respectively. The value is valid, usually the origin.
Within this page the values are all real numbers.
Examples of points in 3 dimensional space.
[edit | edit source]Distance between 2 points
[edit | edit source]
 Length Length Length Consider the point What is the distance from point to the origin? Point is the projection of on to the plane of Calculate length Then length Length In this case The general case: For two points and the distance Length is the special case in which The distance may be in which case and are the same point. |
The line in 3 dimensions
[edit | edit source]
as 2 points[edit | edit source]
as point and 3 direction numbers[edit | edit source]
|
Angle between two lines
[edit | edit source]
 In the diagram line has direction numbers Point has coordinates Line has direction numbers and point has coordinates Length Length Length By the cosine rule
If all values are direction cosines, If the lines are normal. If or the lines are parallel.
|
Normal to 2 lines
[edit | edit source]|
A line normal or perpendicular to two lines is normal to each line. Before attempting to calculate the direction numbers of the normal, first verify that the two lines are not parallel. Let the normal have direction numbers Let the 2 lines have direction numbers Then: and
If divisor If divisor Provided that all inputs are valid, then at least one of must be non-zero and at least one of or or must be valid. From above:
Values of that satisfy this condition are:
Proof: Angle between and
Therefore the two groups of direction numbers are normal. Similarly it can be shown that the two groups of direction numbers and are normal. The line normal to and has direction numbers:
|
Normal to 1 line
[edit | edit source]|
If a given line has direction numbers
For example: If the given line has direction numbers If the given line has direction numbers If the given line has direction numbers |
Point and line
[edit | edit source]
 In the diagram line and point are well defined and Point is on line Line is perpendicular to line Calculate the coordinates of point and length Initial considerations:
Calculate direction cosines of line : Calculate direction cosines of line : Calculate Calculate length Calculate length Let point have coordinates Then point lengthlengthlength Calculate length By extending line PQ with constant K[edit | edit source]
|
Points of closest approach
[edit | edit source]|
Points of closest approach are the 2 points at which the distance between 2 skew lines is minimum. Let 2 lines be Calculate point on It's possible that length may be zero in which case points are the same point and the lines intersect.
Let Calculate the direction numbers of the normal:
and point Relative to
or:
This is a system of three equations with three unknowns: If are direction cosines, length
Example 2:
|
The plane in 3 dimensions
[edit | edit source]|
In two dimensions the point that is always equidistant from two fixed points is the line. In three dimensions the point that is always equidistant from two fixed points is the plane. Let point have coordinates Let point have coordinates Distance must be non-zero. Let point have coordinates Then length = length
This equation has the form where:
Normal to the plane:[edit | edit source]
Distances:[edit | edit source]
To visualize the plane:[edit | edit source]
Defining the plane[edit | edit source]
Plane and line[edit | edit source]
Plane and point[edit | edit source]
Plane and plane[edit | edit source]
|
Reviewing:
[edit | edit source]Now that information about the plane is available to the reader, some of the concepts above can be reviewed and simplified.
Point and line[edit | edit source]
Points of closest approach[edit | edit source]
|
Three planes
[edit | edit source]|
The intersection of 3 planes is a point. The word "intersection" implies that the three planes actually intersect. Given three random planes, there are two situations that do not produce a point of intersection:
|
The sphere
[edit | edit source]|
The sphere is the locus of a point that is always a fixed non-zero distance from a given fixed point. Let the point be Let Then
where:
reversing the conversion[edit | edit source]Given a sphere defined as
examples[edit | edit source]
|
Sphere and line
[edit | edit source]|
Given a sphere and a line:
from the center of the sphere is always greater than the radius of the sphere. The possible point/s of intersection may be calculated by trigonometry or by algebra. Given a sphere defined as By trigonometry:[edit | edit source]
By extending line with constant K[edit | edit source]
By algebra:[edit | edit source]
|
Defined as 4 points
[edit | edit source]|
If 4 unique points on surface of sphere are known, the center and radius may be calculated. From above, equation of sphere is: When are known and are unknown the above equation becomes: With four points provided, equation may be used to construct a system of 4 simultaneous equations that, when solved, provide the values For example:
The above matrix of 4 rows by 5 columns is input to function
|
Center as intersection of 3 planes
[edit | edit source]|
Let center of sphere be Let 4 points on surface of sphere be
or
# python code:
point1 = a,b,c = (16,11,29)
point2 = g,h,j = (17,-5,20)
point3 = k,l,m = (25,3,14)
point4 = n,p,q = (10,19,13)
def plane (point1, point2) :
a,b,c = point1
d,e,f = point2
x,y,z = (a+d)/2, (b+e)/2, (c+f)/2
A,B,C = a-d, b-e, c-f
if A == B == C == 0 :
print ('plane (point1, point2) : distance between point1 and point2 must be non-zero.')
return None
''' Ax + By + Cz + D = 0 '''
D = -( A*x + B*y + C*z )
return (A,B,C,D)
input = []
for point in (point2, point3, point4) :
A,B,C,D = plane(point1,point)
input.append( (A,B,C,D) )
print (input)
output = solve3by4(input)
print (output)
[
(-1, 16, 9, -252.0),
(-9, 8, 15, -194.0),
(6, -8, 16, -294.0)
]
(13.0, 7.0, 17.0) # Coordinates of center of sphere.
For function |
Third line
[edit | edit source]|
Given:
Calculate direction numbers of line3.
|
Rotate line through given angle
[edit | edit source]|
Given:
Calculate:
This is a special case of function # python code.
def rotateLine(ABCD, A1B1C1, cosθ, flag=None) :
'''
ABCD contains the direction numbers A,B,C of the normal to the plane.
A1B1C1 contains [A1,B1,C1], direction numbers of line1.
cosθ is cosine of angle between line1 and line2.
if flag is non-zero, cosθ is an angle in degrees and cosθ is to be calculated.
direction_numbers1,direction_numbers2 = rotateLine(ABCD, A1B1C1, cosθ, flag=None)
'''
rotateLine__ = 'rotateLine(ABCD, A1B1C1, cosθ, flag=None) : '
if flag :
angleInDegrees = cosθ
angleInRadians = angleInDegrees*math.pi/180
cosθ = math.cos(angleInRadians)
A,B,C,D = ABCD
A1,B1,C1 = A1B1C1
# Verify that direction numbers are normal.
sum = A*A1 + B*B1 + C*C1
# If sum is close to zero, make it zero.
sum = (sum,0)[abs(sum) < 1e-14]
if sum :
print ( rotateLine__ + 'error 1. direction numbers not normal, sum =',sum)
return None
#output = dcOfLine3 ([A1,B1,C1], [A2,B2,C2], cos1, cos2)
output = dcOfLine3 ([A1,B1,C1], [A,B,C], cosθ, 0)
# cosθ is associated with line1 [A1,B1,C1]
# 0 = cos(90) is asociated with normal to plane [A,B,C]
return output
A simple example: ABCD = A,B,C,D = 0,0,1,0 # Plane of x and y.
A1B1C1 = A1,B1,C1 = 0,1,0 # Y axis
output = rotateLine(ABCD, A1B1C1, 45, 1) # 45 degrees.
print (output)
[[0.7071067811865475, 0.7071067811865476, 0.0], # 45 degrees to right of Y axis.
[-0.7071067811865475, 0.7071067811865476, 0.0]] # 45 degrees to left of Y axis.
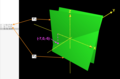
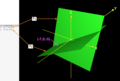
Spokes of a wheel[edit | edit source]
|
By algebra
[edit | edit source]|
Ensure that all values are direction cosines. The relevant equations are:
The function above simplifies to:
def dcOfLine3_byAlgebra (dn1, dn2, cos1, cos2) :
'''
direction cosines of line 3 by algebra
output = dcOfLine3_byAlgebra ([A1,B1,C1], [A2,B2,C2], cos1, cos2)
output may be:
None
[] no solution
[[a3,b3,c3]] 1 group of direction cosines
[[a3a,b3a,c3a], [a3b,b3b,c3b]] 2 groups of direction cosines
'''
if 1 >= cos1 >= -1 : pass
else :
print ('dcOfLine3_byAlgebra (dn1, dn2, cos1, cos2) : error in cos1.')
return None
if 1 >= cos2 >= -1 : pass
else :
print ('dcOfLine3_byAlgebra (dn1, dn2, cos1, cos2) : error in cos2.')
return None
A1,B1,C1 = dn1
if A1 == B1 == C1 == 0 :
print ('dcOfLine3_byAlgebra (dn1, dn2, cos1, cos2) : dn1 all zero.')
return None
A2,B2,C2 = dn2
if A2 == B2 == C2 == 0 :
print ('dcOfLine3_byAlgebra (dn1, dn2, cos1, cos2) : dn2 all zero.')
return None
A3 = B1*C2 - C1*B2
if not A3 :
B3 = C1*A2 - A1*C2
if not B3 :
C3 = A1*B2 - B1*A2
if not C3 :
print ('dcOfLine3_byAlgebra (dn1, dn2, cos1, cos2) : dn1 and dn2 are parallel.')
return None
# Convert direction numbers to direction cosines:
K1 = (A1*A1 + B1*B1 + C1*C1)**.5
a1,b1,c1 = A1/K1, B1/K1, C1/K1
K2 = (A2*A2 + B2*B2 + C2*C2)**.5
a2,b2,c2 = A2/K2, B2/K2, C2/K2
debug = 1
output = dcOfLine3_byAlgebra_ ([a1,b1,c1], [a2,b2,c2], cos1, cos2)
if isinstance(output,list) :
if debug : print (1,output) # output line 1
return output
output = dcOfLine3_byAlgebra_ ([b1,c1,a1], [b2,c2,a2], cos1, cos2)
if isinstance(output,list) :
output = [ [v[2],v[0],v[1]] for v in output ]
if debug : print (2,output) # output line 2
return output
output = dcOfLine3_byAlgebra_ ([c1,a1,b1], [c2,a2,b2], cos1, cos2)
if isinstance(output,list) :
output = [ [v[1],v[2],v[0]] for v in output ]
if debug : print (3,output) # output line 3
return output
Examples[edit | edit source]
|
Links to Related Topics
[edit | edit source]Functions_(mathematics)/Graphs/Coordinations
Functions_(mathematics)/Graphs


























































![{\displaystyle OQ=[A,B,C]=[x_{2}-x_{1},y_{2}-y_{1},z_{2}-z_{1}]=[4,3,12].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddf76bda7fbc4578fcf1436a8fa6d529d673b5c2)
![{\displaystyle ((x_{1},y_{1},z_{1}),\ [A_{1},B_{1},C_{1}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/926cd202848e11bda925d006d117431b3ee1b0ee)
![{\displaystyle [A_{1},B_{1},C_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a92b39bfaa8eee6bba4e1f64edaf0b3290f967cc)

















![{\displaystyle [A,B,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55f0f53888fe1959dd012fbc91f17aa101f2fde5)


![{\displaystyle [A,B,C]=[0,0,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8b2c72412c2980329fad00d43862b967d996984)




![{\displaystyle [A_{1},B_{1},C_{1}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11b4883699a5bb609e30b5fdaed7c020b1bca3ce)


![{\displaystyle [A_{2},B_{2},C_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8149ee6f240fef2e38ee3c91312aaf1b0e6dde63)











![{\displaystyle [A_{2},B_{2},C_{2}]=[1,0,0].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63810263135f596fc1fe1a8d27004fbfc9776a9b)





![{\displaystyle [KA,KB,KC].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e82abc8663356a03c40e21a27404219640f36a2)



![{\displaystyle [-KA,-KB,-KC],\ \cos(\theta )=-1,\ \theta =180^{\circ }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efdacee76411857950b930dfb385a4baf91db686)


![{\displaystyle [A_{2},B_{2},C_{2}]=[KA_{1},KB_{1},KC_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dcd57c313ff10febbae6a67e3a6ede8cd57cff1)





![{\displaystyle [A_{2},B_{2},C_{2}],\ [A_{3},B_{3},C_{3}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39e7e60aa648d92a6dd0a9e4c3a3eef0b1331da4)















![{\displaystyle [B_{3}C_{2}-B_{2}C_{3},\ A_{2}C_{3}-A_{3}C_{2},\ B_{2}A_{3}-B_{3}A_{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/020ed4e99c0b74a6160a66744f0a392af83c093d)
![{\displaystyle [A_{2},B_{2},C_{2}]:}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eed09807719227edea9d40c3abe41657e194c853)






![{\displaystyle [A_{3},B_{3},C_{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e4be68a8bfc6e7c751a776f71fe3cd6506c2142)



![{\displaystyle [A_{3},B_{3},C_{3}]=[KA_{2},KB_{2},KC_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17058dfa05b2163abd6a316de3ca8781474902a8)

![{\displaystyle [A_{2},B_{2},C_{2}],[A_{3},B_{3},C_{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e684762cc7fb6fb9a54ddfb18a538da0b4b8683)
![{\displaystyle [A_{1},B_{1},C_{1}]=[0,0,0].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9eccb8d064be04124d917b2a69b372749f2d2329)












![{\displaystyle [A1,B1,C1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b340149f226cba74d63acc0611c11b8993bae8a3)

![{\displaystyle [A2,B2,C2].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/809861aa8d88ef56307404071342fb182862d531)


















![{\displaystyle [A_{2},B_{2},C_{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c485b71f8ade45466adc3439cf51e99e2c5b391)
![{\displaystyle [A_{3},B_{3},C_{3}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05f0e029af0ee1f31431cb5e02d4fd1a4961f408)




































![{\displaystyle [d-a,e-b,f-c]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc466c21d4eb62c32183b0f20b745a24843e3da1)
![{\displaystyle [{\frac {A}{2}},{\frac {B}{2}},{\frac {C}{2}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63fde96ba5b7a68f3fe3e6566a0eee5a9abcd079)

![{\displaystyle [A,B,C].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c70004a749dd4d9e07cedf639cbce35409946f5)



































![{\displaystyle ((x_{1},y_{1},z_{1}),[A_{1},B_{1},C_{1}]):}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff6ec39e3de1b733e9318fcdd84d4ce621f27f99)














![{\displaystyle [5,25,-7].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8916224368b555209d99bfdeef402b4366a026c)



![{\displaystyle =[A_{1},B_{1},C_{1}]=[{\frac {5}{\sqrt {699}}},{\frac {25}{\sqrt {699}}},{\frac {-7}{\sqrt {699}}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/810c1de9cda757ae06103313395e8b54caca8b86)


![{\displaystyle [A,B,C],[A_{1},B_{1},C_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c675b33bd3774757b5dd43a4edd5767a4378fd66)



























































































































































![{\displaystyle [a_{1},b_{1},c_{1}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2941b7a73ad3777ffe710009e4daacd30dd1f25)
![{\displaystyle [a_{2},b_{2},c_{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dd26d4db20dcbabc6ae7302efb6f2961794a642)













![{\displaystyle [a_{1},b_{1},c_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c02e7cd934db03c17d6a9bb3ee4faf66c1d5b3bc)
![{\displaystyle [a_{1},b_{1},c_{1}],\ [a_{2},b_{2},c_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/434457196f5f81247941a5775801ad65466ca00a)














