Solving simultaneous equations

Introduction

The word "simultaneous" implies that two or more equations exist in the same context at the same time.

For example:

$3x+2y-13=0\ \dots \ (1)$

$2x-y-4=0\ \dots \ (2)$

Equations $(1)$ and $(2)$ are 2 simultaneous equations.

When we see two simultaneous equations, it's natural to ask the question: What are the values of $x$ and $y$ that satisfy both equations $(1)$ and $(2)$ ?

To calculate $(x,y)$ common to both $(1)$ and $(2)$ :

$(2)*2\ \dots \ 4x-2y-8=0\ \dots \ (3)$

$(3)+(1)\ \dots \ 7x-21=0;\ x=3.$

Substitute $3$ for $x$ in $(2):\ 2(3)-y-4=0;\ y=2.$

The values $(x,y)=(3,2)$ satisfy both equations $(1)$ and $(2).$

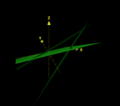
In cartesian coordinate geometry of 2 dimensions, point $(3,2)$ is the point of intersection of two lines $(1)$ and $(2).$ See Figure 1 below.

If the 2 lines are parallel, there is no point of intersection. See Figure 2 below.

The trivial solution $(0,0)$ is a valid solution. See Figure 3 below.

Figure 1. 2 lines that intersect at point (3,2).
Figure 2. When 2 lines are parallel, there is no point of intersection.
Figure 3. The trivial solution x=y=0 is a valid solution.

The information contained in equations $(1)$ and $(2)$ may constitute a matrix:

[
  [3,  2, -13],
  [2, -1,  -4]
]

In fact, in the python programming language, the following statement is valid code:

data = [
  [3,  2, -13],
  [2, -1,  -4]
]

For there to be a point of intersection, data must be valid.

Here are examples of invalid data:

data = [
  [3,  2, -13],  # Both lines are parallel.
  [6,  4,  -5]   # See Figure 2 above.
]

data = [
  [3,  2, -13],
  [0,  0,  -4] # Empty row, representing equation 0x + 0y - 4 = 0.
]

data = [
  [3,  0, -13], # Empty column representing 2 parallel lines:
  [2,  0,  -4]  # 3x = 13 and 2x = 4.
]

The matrix above with name "data" is described as matrix "2 by 3," meaning that it contains 2 rows with 3 columns or 3 members per row.

Solving 2 by 3

Below is python code containing function solve2by3 (input). The function accepts as input a matrix like data above.

After the code are examples of invocation with both good data and bad data.

import sys

def solve2by3 (input) :
    '''
input represents system:
a1*x + b1*y + c1 = 0
a2*x + b2*y + c2 = 0

input = (
(a1,b1,c1),
(a2,b2,c2),
)

To invoke:
x,y = solve2by3 (input)
Function solve2by3 () may return None.

input is not changed by this function.
'''
    def solve2by3_(input) :
        row1,row2 = input
        a1,b1,c1 = row1
        a2,b2,c2 = row2

        if ( (a1 == b1 == 0) or (a2 == b2 == 0) ) :
            print ('solve2by3() : empty row in input.')
            return None
        if (a1 == a2 == 0) or (b1 == b2 == 0) :
            print ('solve2by3() : empty column in input.')
            return None
        if a1*b2 == a2*b1 :
            print ('solve2by3() : parallel input.')
            return None
        if c1 == c2 == 0 :
            # Column is empty. However, trivial solution is valid.
            return 0,0

# Arrange input, if necessary, to ensure that a1 is non-zero.
        if a1 : pass
        else :
            row1,row2 = row2,row1
            a1,b1,c1 = row1
            a2,b2,c2 = row2

# The matrix is:
# a1, b1, c1 with a1 non-zero.
# a2, b2, c2
# Process row2, if necessary,  so that a2 becomes 0.

        if a2 :
            if a2 == a1 :
                b2_,c2_ =  b1-b2, c1-c2
            else:
                L1 = [a2*v for v in row1]
                L2 = [a1*v for v in row2]
                zero,b2_,c2_ = [ L1[p]-L2[p] for p in (0,1,2) ]
                if zero :
                    # Theoretically this should not happen.
                    # It may happen if, for example, limited precision
                    # of floats causes small rounding errors.
                    print ('solve2by3() : Internal error 1.')
                    return None
        else : b2_,c2_ =  b2,c2

# The matrix is:
# a1, b1,  c1  with a1 non-zero
# 0,  b2_, c2_ and a2 zero.

        # 0*x + b2_*y + c2_ = 0
        # b2_*y = - c2_
        y = -c2_/b2_

        # a1*x + b1*y + c1 = 0
        # a1*x = -( b1*y + c1 )
        x = -(c1 + b1*y)/a1 # Here is why a1 must be non-zero.

        return x,y

# Following is python code used for trapping errors
# that may occur in function solve2by3_() above.
    output = error = ''
    try : output = solve2by3_(input)
    except : error = sys.exc_info()[:2]
    if (output == None) or error :
        if error :
            print ('solve2by3() :')
            print ('  error detected in processing.')
            print ('   ', error)
        print ('  input =')
        print ('   ', input[0])
        print ('   ', input[1])
        return None
    return output

Invocation with good data:

output = solve2by3([
  [3,  2, -13],
  [2, -1,  -4]
])
print (output)

(3.0, 2.0)

Invocation with bad or invalid data:

output = solve2by3([
  [3,  2, -13],  # Both lines are parallel.    
  [6,  4,  -5]   # See Figure 2 above.         
])
print (output)

solve2by3() : parallel input.
  input =
    [3, 2, -13]
    [6, 4, -5]
None

output = solve2by3([
  [3,  2, -13, 7], # Input matrix not exactly 2 by 3.
  [6,  4,  -5]
])
print (output)

solve2by3() :
  error detected in processing.
    (<class 'ValueError'>, ValueError('too many values to unpack (expected 3)',))
  input =
    [3, 2, -13, 7]
    [6, 4, -5]
None

output = solve2by3([
  [3,  0, 2],
  [6,  0, 4]
])
print (output)

solve2by3() : empty column in input.
  input =
    [3, 0, 2]
    [6, 0, 4]
None

Reversing the process

Linear Function

**Figure 1. Diagram of line defined by 2 points.**
2 points are: $(-5,4),(3,1).$
Equation of line is: $3x+8y-17=0.$

Examples above calculate the point of intersection of 2 lines.

An example of reversing the process is this task:

Given two points $(x_{1},y_{1}),(x_{2},y_{2})$ calculate equation of line containing these 2 points.

Equation of line is of format $Ax+By+C=0,$

For example: $3x+2y+10=0\ \dots \ (1).$

Equation $(1)$ can be expressed as $6x+4y+20=0$ or $-9x-6y-30=0.$

Also, there appear to be 3 unknowns, but only two sets of values are required to define the line.

Assume $C=1$ and the 2 relevant equations are:

$Ax_{1}+By_{1}+1=0$

$Ax_{2}+By_{2}+1=0$

To solve for $A,B:$

$x_{1}A+y_{1}B+1=0$

$x_{2}A+y_{2}B+1=0$

Suppose the line is defined by points $(3,1),(-5,4):$

# python code:
input = [
    [3,1,1],
    [-5,4,1],
]
result = solve2by3 (input)
print (result)

(-0.17647058823529413, -0.47058823529411764)

Desired equation is: $-0.17647058823529413\cdot x-0.47058823529411764\cdot y+1=0\ \dots \ (2).$

To improve appearance of $(2):$

# python code:

print (A/B)

0.37500000000000006

Let $A,B=3,8$ and check:

# python code

A,B = 3,8

p1 = x1,y1 = 3,1
p2 = x2,y2 = -5,4

for v in (p1,p2) :
    x,y = v
    C = -(A*x + B*y)
    s1 = 'C'
    print (s1, eval(s1))

C -17
C -17

Desired equation $(2)$ becomes $3x+8y-17=0\ \dots \ (3).$

Wrong assumptions

**Figure 2. Diagram of line defined by 2 points and passing through origin.**
2 points are: $(3,2),(6,4).$
Equation of line is: $2x-3y=0.$
Non-zero value for coefficient $C$ is impossible.

Sometimes you create a matrix that seems correct, but it fails to produce a result. Here is such an example:

What is equation of line defined by points $(3,2),(6,4)?$

As above assume that $C=1.$

# python code:

p1 = x1,y1 = 3,2 
p2 = x2,y2 = 6,4
input = [
    [x1,y1,1],
    [x2,y2,1],
]

result = solve2by3 (input)
print (result)

This assumption failed:

solve2by3() : parallel input.
  input =
    [3, 2, 1]
    [6, 4, 1]
None

Assume that $A=1.$

# python code:

# 1(x1) + B(y1) + 1(C) = 0
# 1(x2) + B(y2) + 1(c) = 0

# y1(B) + 1(C) + x1 = 0
# y2(B) + 1(C) + x2 = 0

input = [
    [y1,1,x1], # Notice that input has been
    [y2,1,x2], # rotated left by one column.
]

result = solve2by3 (input)
print (result)

(-1.5, 0.0)

Equation of line is: $1\cdot x+(-1.5)\cdot y+0=0$ or $2x-3y=0$

This line includes the origin. Therefore constant $C$ cannot be non-zero.

Generally:

Without rotation, $A,B={\text{result}}$ and $C=1.$

With rotation left by one column, $B,C={\text{result}}$ and $A=1.$

In this case:

# python code:
>>> B,C = result ; A = 1
>>> A,B,C
>>> 1,-1.5,0

For example of big matrix that failed the first time, but was successful the second time, see cubic resistive network below.

Solving 3 by 4

Below is python code containing function solve3by4 (input). The function accepts as input a 3 by 4 matrix like that described in the code comments.

In 3d coordinate geometry the equations (1), (2), (3) are the equations of 3 planes and the solution of the system is the point of intersection of the 3 planes.

Given 3 random planes, there are 2 conditions that do not produce a point of intersection:

If 2 of the planes are parallel. See Figure 1 below.

If the 3 planes form a "tent" or "delta." See Figure 2, 3 or 4 below. A special case of this condition occurs when size of "tent" is zero, in which case all three planes intersect on a common line and there is an infinite number of solutions. See Figure 5 below.

The trivial solution $(0,0,0)$ is valid. See Figure 6 below.

Figure 1. When 2 planes are parallel, there is no point of intersection.
Figure 2. Triangular tube, 3 planes that never intersect.
Figure 3. 3 planes that form a "tent," view 1. There is no point of intersection.
Figure 4. 3 planes that form a "tent," view 2. There is no point of intersection.
Figure 5. 3 planes that intersect on a common line. Points $(6,6,1),$ $(7,7,4),$ $(8,8,7)$ are on this line and are common to all 3 planes.
Figure 6. 3 planes that intersect at origin (0, 0, 0).

def solve3by4 (input) :
    '''
input represents system:
a1*x + b1*y + c1*z + d1 = 0 ... (1)
a2*x + b2*y + c2*z + d2 = 0 ... (2)
a3*x + b3*y + c3*z + d3 = 0 ... (3)

input = (
(a1,b1,c1,d1),
(a2,b2,c2,d2),
(a3,b3,c3,d3),
)

To invoke:
x,y,z = solve3by4 (input)
Function solve3by4 () may return None.

input is not changed by this function.
'''
    def checkDirectionNumbers (input) :
        row1,row2,row3 = input
        a1,b1,c1,d1 = row1
        a2,b2,c2,d2 = row2
        a3,b3,c3,d3 = row3
# The direction numbers of the lines of intersection.
        dn1 = [b3*c2-b2*c3, a2*c3-a3*c2, b2*a3-b3*a2]
        if dn1[0] == dn1[1] == dn1[2] == 0 :
            print ('checkDirectionNumbers() : 2 rows parallel, 2 and 3.')
            return
        dn2 = [b3*c1-b1*c3, a1*c3-a3*c1, b1*a3-b3*a1]
        if dn2[0] == dn2[1] == dn2[2] == 0 :
            print ('checkDirectionNumbers() : 2 rows parallel, 1 and 3.')
            return
        dn3 = [b1*c2-b2*c1, a2*c1-a1*c2, b2*a1-b1*a2]
        if dn3[0] == dn3[1] == dn3[2] == 0 :
            print ('checkDirectionNumbers() : 2 rows parallel, 1 and 2.')
            return
# Are 2 lines of intersection parallel?
# If so, and no 2 planes are parallel, the 3 planes form a tent.
        a2,b2,c2 = dn2
        a3,b3,c3 = dn3
        dn1 = [b3*c2-b2*c3, a2*c3-a3*c2, b2*a3-b3*a2]
        if dn1[0] == dn1[1] == dn1[2] == 0 :
            print ('checkDirectionNumbers() : 3 rows form a tent.');
            return

    def solve3by4_(input) :
        row1,row2,row3 = input
        a1,b1,c1,d1 = row1
        a2,b2,c2,d2 = row2
        a3,b3,c3,d3 = row3

        if (a1 == b1 == c1 == 0) or (a2 == b2 == c2 == 0) or (a3 == b3 == c3 == 0) :
            print ('solve3by4() : empty row in input.')
            return None
        if (a1 == a2 == a3 == 0) or (b1 == b2 == b3 == 0) or (c1 == c2 == c3 == 0) :
            print ('solve3by4(). empty column in input.')
            return None
        if (d1 == d2 == d3 == 0) :
            # This empty column means that trivial solution is valid.
            return 0,0,0

# Sort input if necessary so that a1 is non-zero.
        if a1 : pass
        elif a2 :
            row1,row2 = row2,row1
            a1,b1,c1,d1 = row1
            a2,b2,c2,d2 = row2
        else :
            row1,row3 = row3,row1
            a1,b1,c1,d1 = row1
            a3,b3,c3,d3 = row3

# The matrix is:
# a1, b1, c1, d1 with a1 non-zero.
# a2, b2, c2, d2
# a3, b3, c3, d3

# Process rows, if necessary, so that a2,a3 become zero.

        if a2 :
            L1 = [a2*v for v in row1]
            L2 = [a1*v for v in row2]
            zero,b2_,c2_,d2_ = [ L1[p]-L2[p] for p in (0,1,2,3) ]
        else : zero,b2_,c2_,d2_ =  a2,b2,c2,d2

        if a3 :
            L1 = [a3*v for v in row1]
            L2 = [a1*v for v in row3]
            zero,b3_,c3_,d3_ = [ L1[p]-L2[p] for p in (0,1,2,3) ]
        else : zero,b3_,c3_,d3_ =  a3,b3,c3,d3

# The matrix is:
# a1, b1,  c1,  d1 with a1 non-zero.
# 0,  b2_, c2_, d2_
# 0,  b3_, c3_, d3_
        data1 = (
(b2_, c2_, d2_),
(b3_, c3_, d3_),
)
        data2 = solve2by3(data1)
        if data2 == None :
            checkDirectionNumbers (input) # If solve2by3() fails, this line shows why.
            return None
        y,z = data2
        # a1*x + b1*y + c1*z + d1 = 0
        # a1*x = -( b1*y + c1*z + d1 )
        x = -(b1*y + c1*z + d1)/a1 # Here is why a1 must be non-zero.

        return x,y,z

    output = error = ''
    try : output = solve3by4_(input)
    except : error = sys.exc_info()[:2]

    if (output == None) or error :
        if error :
            print ('solve3by4() :')
            print ('  error detected in processing.')
            print ('   ', error)
        print ('  input of solve3by4() =')
        print ('   ', input[0])
        print ('   ', input[1])
        print ('   ', input[2])
        return None
    return output

Below are examples of invocation with both good data and bad data.

Invocation with good data:

output = solve3by4([
  [2,  -1, 3, -17],
  [1,  3, 2, -25] ,
  [3,  2, -1, -12] ,
])
print (output)

(3.0, 4.0, 5.0)

output = solve3by4([
  [12,  -12, -5, -24],
  [-6,   15,  8,  12] ,
  [ 0,   10,  3,   0] ,
])
print (output)

(2.0, 0.0, -0.0)

Invocation with bad or invalid data:

output = solve3by4([
    [20, 16, 2, 17],
    [-77, -27, -25, -24],
    [81, 45, 18, 43]
])
print (output)

solve2by3() : parallel input.
  input =
    (-692, 346, -829)
    (396, -198, 517)
checkDirectionNumbers() : 3 rows form a tent.
  input of solve3by4() =
    [20, 16, 2, 17]
    [-77, -27, -25, -24]
    [81, 45, 18, 43]
None

output = solve3by4([
    [-34, -6, 34, -32],
    [82, 14, -82, 72],
    [-59, -45, 59, -88]
])
print (output)

solve2by3() : empty column in input.
  input =
    (-16, 0, -176)
    (-1176, 0, -1104)
checkDirectionNumbers() : 3 rows form a tent.
  input of solve3by4() =
    [-34, -6, 34, -32]
    [82, 14, -82, 72]
    [-59, -45, 59, -88]
None

output = solve3by4([
    [34, -5, -21, 30],
    [-54, -33, 63, 62],
    [18, 11, -21, 38]
])
print (output)

solve2by3() : parallel input.
  input =
    (1392, -1008, -3728)
    (-464, 336, -752)
checkDirectionNumbers() : 2 rows parallel, 2 and 3.
  input of solve3by4() =
    [34, -5, -21, 30]
    [-54, -33, 63, 62]
    [18, 11, -21, 38]
None

output = solve3by4([
    [20, 16, 2, 17],
    [-77, -27, '-25', -24],
    [81, 45, 18, 43]
])
print (output)

solve3by4() :
  error detected in processing.
    (<class 'TypeError'>, TypeError("unsupported operand type(s) for -: 'int' and 'str'",))
  input of solve3by4() =
    [20, 16, 2, 17]
    [-77, -27, '-25', -24]
    [81, 45, 18, 43]
None

Reversing the Process

Quadratic function

A quadratic function $y=f(x)=Ax^{2}+Bx+C$ is defined by 3 points: $(-2,9.0),(5,4.8),(10,13.8).$

What is $f(x)?$

$y=Ax^{2}+Bx+C$

$A,B,C$ are 3 unknowns.

$x^{2}(A)+x(B)+1(C)-y=0$

# python code:

x1,y1 = -2, 9
x2,y2 =  5, 4.8
x3,y3 = 10, 13.8

input = [
    [x1**2, x1, 1, -y1],
    [x2**2, x2, 1, -y2],
    [x3**2, x3, 1, -y3],
]

A, B, C = solve3by4 (input)
s1 = 'A,B,C'
print (s1, eval(s1))

A,B,C (0.2, -1.2, 5.8)

$y=f(x)=0.2x^{2}-1.2x+5.8$

Wrong assumptions

**Figure 2. Graph of plane containing X axis.**
Because plane passes through origin, non-zero value for coefficient $D$ is impossible.
Because plane is parallel to $X$ axis, non-zero value for coefficient $A$ is impossible.

In 3 dimensions a plane ( $Ax+By+Cz+D=0$ ) is defined by 3 points: $(5,3,-2),(-1,12,-8),(37,15,-10).$

What is equation of plane?

$Ax+By+Cz+D=0$

$xA+yB+zC+D=0$

Assume that $D=1.$

$xA+yB+zC+1=0$

# python code

pt1 = x1,y1,z1 = (5, 3, -2)
pt2 = x2,y2,z2 = (-1, 12, -8)
pt3 = x3,y3,z3 = (37, 15, -10)

input = [
    [ 5,  3,  -2, 1],
    [-1, 12,  -8, 1],
    [37, 15, -10, 1],
]

result = solve3by4 (input)
s1 = 'result'
print (s1, eval(s1))

solve2by3() : parallel input.
  input =
    (-63, 42, -6)
    (36, -24, 32)
checkDirectionNumbers() : 3 rows form a tent.
  input of solve3by4() =
    (5, 3, -2, 1)
    (-1, 12, -8, 1)
    (37, 15, -10, 1)
result None

Input was invalid. Rotate input left and try again.

# python code.

input = [
    [ 3,  -2, 1,  5],
    [12,  -8, 1, -1],
    [15, -10, 1, 37],
]

result = solve3by4 (input)
s1 = 'result'
print (s1, eval(s1))

solve2by3() : empty column in input.
  input =
    (0, 9, 63)
    (0, 12, -36)
checkDirectionNumbers() : 3 rows form a tent.
  input of solve3by4() =
    (3, -2, 1, 5)
    (12, -8, 1, -1)
    (15, -10, 1, 37)
result None

Input was invalid. Rotate input left and try again.

input = [
    [ -2, 1,  5,  3],
    [ -8, 1, -1, 12],
    [-10, 1, 37, 15],
]

result = solve3by4 (input)
s1 = 'result'
print (s1, eval(s1))

result (1.5, 0, 0)

Without rotation: $A,B,C={\text{result}}$ and $D=1.$

With rotation left: $B,C,D={\text{result}}$ and $A=1.$

With another rotation left: $C,D,A={\text{result}}$ and $B=1.$

# python code:
C, D, A = (1.5, 0, 0) ; B = 1
A, B, C, D

(0, 1, 1.5, 0)

Equation of plane is: $0x+1y+1.5z+0=0$ or $2y+3z=0$

Solving M by (M+1)

Below is python code containing function solveMbyN (input). The function accepts as input a 4 by 5 matrix (or greater) like that described in the code comments.

This function is recursive, calling itself with M being reduced by 1 with each recursive invocation until the matrix is size 3 by 4 in which case function solve3by4() is called.

# python code

import decimal
Decimal = decimal.Decimal
getcontext = decimal.getcontext

def reduceRow (row) :
    '''
This function calculates the max(abs) of all values in row,
divides all values by the max(abs) and returns the result.
[27, -15, 42] becomes [27/42, -15/42, 42/42].
Very small values are converted to zero.

To invoke:
output = reduceRow (row)
output is list or None
'''
    if False in [ isinstance(v,Decimal) for v in row ] :
        print ('reduceRow: non Decimal in input.', { type(v) for v in row })
        return None
    max = sorted([ abs(v) for v in row ])[-1]
    row = [ v/max for v in row ]
    almostZero = Decimal('1e-' + str( getcontext().prec ))
    row = [ (v, Decimal(0))[abs(v) < almostZero] for v in row ]
    return row

enable_reduceRow = 0

def solveMbyN (input) :
    '''
input represents system:
a0*w + b0*x + c0*y + d0*z + e0 = 0
a1*w + b1*x + c1*y + d1*z + e1 = 0
a2*w + b2*x + c2*y + d2*z + e2 = 0
a3*w + b3*x + c3*y + d3*z + e3 = 0
or greater.
This solves a matrix of M rows by N columns where N = M+1 and M >= 2

input = [
(a0,b0,c0,d0,e0),
(a1,b1,c1,d1,e1),
(a2,b2,c2,d2,e2),
(a3,b3,c3,d3,e3),
]

To invoke:
w,x,y,z = solveMbyN (input)
Function solveMbyN () may return None.

If input is size 15 by 16:
v1,v2,v3, .... ,v14,v15 = solveMbyN (input)

input is not changed by this function.
'''
    def solveMbyN_(input) :
        input = [ list(v) for v in input ]
        # input is now local, hard copy of original input.
        # This ensures that original input is not changed by this function.

        numberOfRows = len(input)
        numberOfColumns = numberOfRows+1

        if numberOfRows < 2 :
            print ('solveMbyN()! len(input) < 2.')
            return None
        if numberOfRows == 2 : return solve2by3(input)
        if numberOfRows == 3 : return solve3by4(input)

        for row in range (0, numberOfRows) :
            if len(input[row]) != numberOfColumns :
                print ('solveMbyN()! row with bad length.')
                print ('    row number',row,'of',numberOfRows,'rows has length',len(input[row]),'.')
                return None
            if True not in [ bool(v) for v in input[row][:-1] ] :
                print ('solveMbyN()! empty row in input, row number',row,'of',numberOfRows,'rows.')
                return None

        for column in range (0, numberOfRows) :
            sum = 0
            for row in range (0, numberOfRows) :
                sum = bool(input[row][column])
                if sum : break
            if not sum :
                print ('solveMbyN()! empty column in input. column number',column,'of',numberOfRows,'columns.')
                return None

        for column in (numberOfRows,) :
            sum = 0
            for row in range (0, numberOfRows) :
                sum = bool(input[row][column])
                if sum : break
            if not sum :
                # Empty column. Trivial solution is valid.
                return (0,) * numberOfRows

        if enable_reduceRow :
            # For matrices greater than 10 by 11 enable this piece of code.
            for row in range (0, numberOfRows) :
                data = reduceRow (input[row])
                if isinstance(data,list) :
                    input[row] = data

# Arrange input if necessary so that a0 is non-zero.
        if not input[0][0] :
            for p in range (1, numberOfRows) :
                if input[p][0] :
                    input[p], input[0] = input[0], input[p]
                    break
# The matrix is:
# [a0,b0,c0,d0,e0], with a0 non-zero,
# [a1,b1,c1,d1,e1],
# [a2,b2,c2,d2,e2],
# [a3,b3,c3,d3,e3],

# Process rows so that a1, a2, a3, .... become zero.
        a0 = input[0][0]
        for p in range (1, numberOfRows) :
            ap = input[p][0]
            if ap :
                L0 = [ input[0][q]*ap for q in range (0, numberOfColumns) ]
                Lp = [ input[p][q]*a0 for q in range (0, numberOfColumns) ]
                L_ = [ L0[q]-Lp[q] for q in range (0, numberOfColumns) ]
                if L_[0] :
                    # This should not happen.
                    print ('solveMbyN()! internal error 1.')
                    return None
                input[p] = L_

# The matrix is:
# [a0, b0, c0, d0, e0], with a0 non-zero,
# [ 0,b1_,c1_,d1_,e1_],
# [ 0,b2_,c2_,d2_,e2_],
# [ 0,b3_,c3_,d3_,e3_],
        data1 = [ input[p][1:] for p in range (1, numberOfRows) ]
# data1 = [
# [b1_,c1_,d1_,e1_],
# [b2_,c2_,d2_,e2_],
# [b3_,c3_,d3_,e3_] ]

        data2 = solveMbyN(data1) # Here is where function solveMbyN() calls itself.
        if data2 == None : return None
        topRow = input[0][1:]
# b0, c0, d0, e0 topRow
#  x,  y,  z     data2
        listOfProducts = [ topRow[p]*data2[p] for p in range (0, len(data2)) ] + topRow[-1:]
# listOfProducts = [ b0*x, c0*y, d0*z, e0 ]
        sumOfProducts = [ sum for sum in (0,) for p in listOfProducts for sum in (sum+p,) ][-1]
# sumOfProducts = [ b0*x, b0*x+c0*y, b0*x+c0*y+d0*z, b0*x+c0*y+d0*z+e0 ][-1]
# sumOfProducts =  b0*x + c0*y + d0*z + e0
#           a0*w + b0*x + c0*y + d0*z + e0 = 0
#           a0*w + sumOfProducts = 0

        w = -sumOfProducts/a0 # Here is why a0 must be non-zero.

        return (w,) + data2

    output = error = ''
    try : output = solveMbyN_(input)
    except : error = sys.exc_info()[:2]
    if (output == None) or error :
        if error :
            print ('solveMbyN()!')
            print ('  error detected in processing.')
            print ('   ', error)
        if len(input) >= 4 :
            print ('  input of solveMbyN() with',len(input),'rows =')
            for row in input : print ('   ', row)
        return None
    return output

Below are examples of invocation with both good data and bad data.

Invocation with good data:

L1 = [
[Decimal('-870442133162'), Decimal('239132906684'), Decimal('397660499756'), Decimal('788825405004'), Decimal('156830886652'), Decimal('-87096140169')], 
[Decimal('-112130420352'), Decimal('-93605595828'), Decimal('-185262083472'), Decimal('-93369903383'), Decimal('-497973505065'), Decimal('-766710012513')], 
[Decimal('-142983492168'), Decimal('619713461197'), Decimal('-608752759383'), Decimal('-448477443042'), Decimal('-281161661751'), Decimal('-799463977245')], 
[Decimal('572854919541'), Decimal('-148673693908'), Decimal('341291756040'), Decimal('362403188059'), Decimal('-202136092949'), Decimal('-429932229578')], 
[Decimal('157632861972'), Decimal('330790263276'), Decimal('-836474627955'), Decimal('644295395386'), Decimal('-595590967129'), Decimal('-392835045727')]
]
output = solveMbyN(L1)
print (output)

The following results were produced with decimal precision set at 50:

(
Decimal('-0.06331410760212760088313271882866553044211194694576'), Decimal('1.0969089506763419155148060427588009931309074487534'), Decimal('1.0837038580207682607126722016017867670831200359767'), Decimal('-0.42989566124678842791674322699930461340596671792215'), Decimal('-2.0541601084281682582146753421426610779297051535362')
)

Invocation with bad or invalid data:

output = solveMbyN([
    [-4, -6, 3, -4, -8, -8],
    [1, 0, 2, 5, 1, 7],
    [9, -3, -8, 4, 7, -5],
    [1, -9, 5, -2, 5, -2],
    [1, -3, -6, -3, -6, 6]
])
print (output)

# With each step towards solve2by3() the length of each number in digits can theoretically double.
solve2by3() : parallel input.
  input =
    (-181440, 181440, -101088)
    (90720, -90720, 406944)
checkDirectionNumbers() : 3 rows form a tent.
  input of solve3by4() =
    [-756, -1176, 0, -1872]
    [-324, -744, 240, -936]
    [-324, -384, -120, -264]
  input of solveMbyN() with 4 rows =
    [-6, 11, 16, -4, 20]
    [-66, -5, -20, -44, -92]
    [-42, 23, -12, 12, -16]
    [-18, -21, -16, -32, 16]
  input of solveMbyN() with 5 rows =
    [-4, -6, 3, -4, -8, -8]
    [1, 0, 2, 5, 1, 7]
    [9, -3, -8, 4, 7, -5]
    [1, -9, 5, -2, 5, -2]
    [1, -3, -6, -3, -6, 6]
None

Provided that numbers are small, integers, floats and Decimal objects produce the same results:

output = solveMbyN([
[-4.0, -6.0, 3.0, -4.0, -8.0, -8.0],
[1.0, 0.0, 2.0, 5.0, 1.0, 7.0],
[9.0, -3.0, -8.0, 4.0, 7.0, -5.0],
[1.0, -9.0, 5.0, -2.0, 5.0, -2.0],
[1.0, -3.0, -6.0, -3.0, -6.0, 6.0]
])
print (output)

solve2by3() : parallel input.
  input =
    (-181440.0, 181440.0, -101088.0)
    (90720.0, -90720.0, 406944.0)
checkDirectionNumbers() : 3 rows form a tent.
  input of solve3by4() =
    [-756.0, -1176.0, 0.0, -1872.0]
    [-324.0, -744.0, 240.0, -936.0]
    [-324.0, -384.0, -120.0, -264.0]
  input of solveMbyN() with 4 rows =
    [-6.0, 11.0, 16.0, -4.0, 20.0]
    [-66.0, -5.0, -20.0, -44.0, -92.0]
    [-42.0, 23.0, -12.0, 12.0, -16.0]
    [-18.0, -21.0, -16.0, -32.0, 16.0]
  input of solveMbyN() with 5 rows =
    [-4.0, -6.0, 3.0, -4.0, -8.0, -8.0]
    [1.0, 0.0, 2.0, 5.0, 1.0, 7.0]
    [9.0, -3.0, -8.0, 4.0, 7.0, -5.0]
    [1.0, -9.0, 5.0, -2.0, 5.0, -2.0]
    [1.0, -3.0, -6.0, -3.0, -6.0, 6.0]
None

output = solveMbyN([
[Decimal('-4'), Decimal('-6'), Decimal('3'), Decimal('-4'), Decimal('-8'), Decimal('-8')],
[Decimal('1'), Decimal('0'), Decimal('2'), Decimal('5'), Decimal('1'), Decimal('7')],
[Decimal('9'), Decimal('-3'), Decimal('-8'), Decimal('4'), Decimal('7'), Decimal('-5')],
[Decimal('1'), Decimal('-9'), Decimal('5'), Decimal('-2'), Decimal('5'), Decimal('-2')],
[Decimal('1'), Decimal('-3'), Decimal('-6'), Decimal('-3'), Decimal('-6'), Decimal('6')]
])
print (output)

solve2by3() : parallel input.
  input =
    (Decimal('-181440'), Decimal('181440'), Decimal('-101088'))
    (Decimal('90720'), Decimal('-90720'), Decimal('406944'))
checkDirectionNumbers() : 3 rows form a tent.
  input of solve3by4() =
    [Decimal('-756'), Decimal('-1176'), Decimal('0'), Decimal('-1872')]
    [Decimal('-324'), Decimal('-744'), Decimal('240'), Decimal('-936')]
    [Decimal('-324'), Decimal('-384'), Decimal('-120'), Decimal('-264')]
  input of solveMbyN() with 4 rows =
    [Decimal('-6'), Decimal('11'), Decimal('16'), Decimal('-4'), Decimal('20')]
    [Decimal('-66'), Decimal('-5'), Decimal('-20'), Decimal('-44'), Decimal('-92')]
    [Decimal('-42'), Decimal('23'), Decimal('-12'), Decimal('12'), Decimal('-16')]
    [Decimal('-18'), Decimal('-21'), Decimal('-16'), Decimal('-32'), Decimal('16')]
  input of solveMbyN() with 5 rows =
    [Decimal('-4'), Decimal('-6'), Decimal('3'), Decimal('-4'), Decimal('-8'), Decimal('-8')]
    [Decimal('1'), Decimal('0'), Decimal('2'), Decimal('5'), Decimal('1'), Decimal('7')]
    [Decimal('9'), Decimal('-3'), Decimal('-8'), Decimal('4'), Decimal('7'), Decimal('-5')]
    [Decimal('1'), Decimal('-9'), Decimal('5'), Decimal('-2'), Decimal('5'), Decimal('-2')]
    [Decimal('1'), Decimal('-3'), Decimal('-6'), Decimal('-3'), Decimal('-6'), Decimal('6')]
None

Sphere

In cartesian coordinate geometry of three dimensions a sphere is represented by equation:

$x^{2}+y^{2}+z^{2}+Ax+By+Cz+D=0.$

On the surface of a certain sphere there are 4 known points:

# python code

point1 = (13,7,20)
point2 = (13,7,4)
point3 = (13,-17,4)
point4 = (16,4,4)

What is equation of sphere?

Rearrange equation of sphere to prepare for creation of input matrix:

$(x)A+(y)B+(z)C+(1)D+(x^{2}+y^{2}+z^{2})=0.$

Create input matrix of size 4 by 5:

# python code

input = []
for (x,y,z) in (point1, point2, point3, point4) :
    input += [ ( x, y, z, 1, (x**2 + y**2 + z**2) ) ]

print (input)

[ (13,   7, 20, 1, 618),
  (13,   7,  4, 1, 234),
  (13, -17,  4, 1, 474),
  (16,   4,  4, 1, 288), ] # Matrix containing 4 rows with 5 members per row.

# python code

result = solveMbyN(input)
print (result)

(-8.0, 10.0, -24.0, -104.0)

Equation of sphere is :

$x^{2}+y^{2}+z^{2}-8x+10y-24z-104=0$

Quintic function

A quintic function $y=f(x)=Ax^{5}+Bx^{4}+Cx^{3}+Dx^{2}+Ex+F$ is defined by 6 points: $(-8,0),(-6,0),(-3,0),(1,0),(3,0),(5,10).$

What is $f(x)?$

$y=f(x)=Ax^{5}+Bx^{4}+Cx^{3}+Dx^{2}+Ex+F$

$A,B,C,D,E,F$ are 6 unknowns.

$x^{5}(A)+x^{4}(B)+x^{3}(C)+x^{2}(D)+x(E)+1(F)-y=0$

# python code:

pt1 = x1,y1 = -8,0
pt2 = x2,y2 = -6,0
pt3 = x3,y3 = -3,0
pt4 = x4,y4 = 1,0
pt5 = x4,y5 = 3,0
pt6 = x6,y6 = 5,10

input = []

for pt in (pt1,pt2,pt3,pt4,pt5,pt6) :
    x,y = pt
    input += [[ x**5, x**4, x**3, x**2, x, 1, -y  ]]

print (input)

[[-32768, 4096, -512, 64, -8, 1,   0],
 [ -7776, 1296, -216, 36, -6, 1,   0],
 [  -243,   81,  -27,  9, -3, 1,   0],
 [     1,    1,    1,  1,  1, 1,   0],
 [   243,   81,   27,  9,  3, 1,   0],
 [  3125,  625,  125, 25,  5, 1, -10]]

result = solveMbyN (input)

s1 = 'result'
print (s1, eval(s1))

result (0.0010926573426573423, 0.014204545454545447, 0.027316433566433533, 
       -0.18028846153846156,  -0.3343531468531468,   0.47202797202797203)

From these results the following ratios may be deduced:

${\frac {1}{A}}=915.2;\$ ${\frac {B}{A}}=13;\$ ${\frac {C}{A}}=25;\$ ${\frac {D}{A}}=-165;\$ ${\frac {E}{A}}=-306;\$ ${\frac {F}{A}}=432.$

$y=f(x)={\frac {x^{5}+13x^{4}+25x^{3}-165x^{2}-306x+432}{915.2}}$

Resistive network

A resistive network containing 8 resistors is connected as shown in Figure 1.

What is resistance $R$ between points $P_{1},P_{3}?$

Solve for 8 Branch Currents

**Figure 2. Diagram of resistive network showing all branch currents.**

At any point to which 3 or more conductors are connected, sum of currents = 0.
At point $P_{4}$ currents $i_{1},i_{7}$ flow towards point; current $i_{4}$ flows away from point.
$i_{1}+i_{7}-i_{4}=0.$

In any closed loop sum of voltages = 0.
In loop containing points $P_{1},P_{2}$ voltages $e_{2},e_{8}$ are clockwise; voltage $e_{3}$ is counter-clockwise.
$e_{2}+e_{8}-e_{3}=0.$

Direction of flow through $r_{7},r_{8}$ is assumed and is subject to correction.

Voltage across $r_{1}:$

Using $E=IR,\ e_{1}=i_{1}\cdot r_{1}=r_{1}\cdot a.$

Similarly:

$e_{2}=r_{2}\cdot b.$

$e_{3}=r_{3}\cdot c.$

$\dots \dots$

$e_{8}=r_{8}\cdot h.$

Build a matrix size 8 by 9 which will be input to function solveMbyN().

# Python code:

r1,r2,r3,r4,r5,r6,r7,r8 = 10,20,30,40,50,60,70,80

input = []

# e1 = e2 + e7
# 10a = 20b + 70g
#          10a - 20b + 0c + 0d + 0e + 0f - 70g + 0h + 0 = 0
input += [[r1, - r2,   0,   0,   0,   0, - r7,   0,   0]]

# e3 = e2 + e8
# 30c = 20b + 80h
#          0a - 20b + 30c + 0d + 0e + 0f + 0g - 80h + 0 = 0
input += [[0, - r2,   r3,   0,   0,   0,   0, - r8,   0]]

# e5 = e7 + e4
# 50e = 70g + 40d
#          0a + 0b + 0c - 40d + 50e + 0f - 70g + 0h + 0 = 0
input += [[0,   0,   0, - r4,   r5,   0, - r7,   0,   0]]

# e5 = e8 + e6
# 50e = 80h + 60f
#          0a + 0b + 0c + 0d + 50e - 60f + 0g - 80h + 0 = 0
input += [[0,   0,   0,   0,   r5, - r6,   0, - r8,   0]]

# i7 + i5 + i8 = i2
# g + e + h = b
#          0a - 1b + 0c + 0d + 1e + 0f + 1g + 1h + 0 = 0
input += [[0 ,- 1,   0,   0,   1,   0,   1,   1,   0]]

# i4 = i1 + i7
# d = a + g
#          -1a + 0b + 0c + 1d + 0e + 0f - 1g + 0h + 0 = 0
input += [[-1,   0,   0,   1,   0,   0, - 1,   0,   0]]

# i6 = i3 + i8
# f = c + h
#          0a + 0b - 1c + 0d + 0e + 1f + 0g - 1h + 0 = 0
input += [[0,   0, - 1,   0,   0,   1,   0, - 1,   0]]

# Total input current = 1
# a + b + c = 1
#          1a + 1b + 1c + 0d + 0e + 0f + 0g + 0h - 1 = 0
input += [[1,   1,   1,   0,   0,   0,   0,   0, - 1]]

This last entry can contain almost any arbitrary values. For example:

# Python code:

# i7 = 2.3
input += [[0,   0,   0,   0,   0,   0,   1,   0, - 2.3]]

# e5 = 1.9
input += [[0,   0,   0,   0,   r5,   0,   0,   0, - 1.9]]

Changing this last entry changes all values of $e_{x},i_{x}.$ However, the ratio ${\frac {e_{x}}{i_{x}}}=r_{x}$ remains constant.

input is matrix of size 8 by 9:

[
    [10, -20,  0,   0,  0,   0, -70,   0,  0],  # e1 = e2 + e7,      or r1(i1) - r2(i2) - r7(i7) = 0
    [ 0, -20, 30,   0,  0,   0,   0, -80,  0],  # e3 = e2 + e8,      or r3(i3) - r2(i2) - r8(i8) = 0
    [ 0,   0,  0, -40, 50,   0, -70,   0,  0],  # e5 = e4 + e7,      or r5(i5) - r4(i4) - r7(i7) = 0
    [ 0,   0,  0,   0, 50, -60,   0, -80,  0],  # e5 = e6 + e8,      or r5(i5) - r6(i6) - r8(i8) = 0
    [ 0,  -1,  0,   0,  1,   0,   1,   1,  0],  # i2 = i5 + i7 + i8, or 1(i5) + 1(i7) + 1(i8) - 1(i2) = 0
    [-1,   0,  0,   1,  0,   0,  -1,   0,  0],  # i4 = i1 + i7,      or 1(i4) - 1(i1) - 1(i7) = 0
    [ 0,   0, -1,   0,  0,   1,   0,  -1,  0],  # i6 = i3 + i8,      or 1(i6) - 1(i3) - 1(i8) = 0
    [ 1,   1,  1,   0,  0,   0,   0,   0, -1]   # i1 + i2 + i3 = 1,  or 1(i1) + 1(i2) + 1(i3) - 1 = 0
]

i1,i2,i3,i4,i5,i6,i7,i8 = values_of_i = solveMbyN (input)

s1 = 'values_of_i' ; print(s1,eval(s1))
s1 = 'i1 + i2 + i3' ; print(s1,eval(s1))

values_of_i (0.45727389222364606,  0.3065353746543468,  0.23619073312200717, 
             0.4350171983543536,   0.31685438726647336, 0.24812841437917316, 
            -0.022256693869292507, 0.011937681257165982)
i1 + i2 + i3 1.0

$i_{7}$ has negative value. Reverse $i_{7}$ to make all branch currents positive.

Make all Branch Currents positive

**Figure 3. Diagram of resistive network showing all branch currents positive.**

Make $i_{7}$ positive and check results.

# Python code

i7 *= -1

values_of_e = e1,e2,e3,e4,e5,e6,e7,e8 = [ 
    eval(s1) 
    for s in '12345678' 
    for s1 in [ 'i' + s + '*r' + s ]
]
s1 = 'values_of_e'
print(s1,eval(s1))

values_of_e [ 4.572738922236461,  6.130707493086937,
              7.085721993660215, 17.400687934174144,
             15.842719363323669, 14.88770486275039, 
              1.5579685708504756, 0.9550145005732785]

# python code

t1 = (
'e1+e7-e2',              # e1 + e7 should equal e2
'e2+e8-e3',              # e2 + e8 should equal e3
'e7+e5-e4',              # e7 + e5 should equal e4
'e8+e6-e5',              # e8 + e6 should equal e5

'e1+e4-(e2+e5)',         # e1 + e4 should equal e2 + e5
'e1+e4-(e3+e6)',         # e1 + e4 should equal e3 + e6

'e1+e7+e8-e3',           # e1 + e7 + e8 should equal e3
'e7+e8+e6-e4',           # e7 + e8 + e6 should equal e4

'i1-i7-i4',              # i1 should equal i7 + i4
'i6-i3-i8',              # i6 should equal i3 + i8
'i2+i7-(i8+i5)',         # i2 + i7 should equal i8 + i5
'i1+i2+i3 - (i4+i5+i6)', # Total input current should
                         # equal total output current.
)

for s1 in t1 :
    print(s1,eval(s1))

e1+e7-e2             -8.881784197001252e-16
e2+e8-e3              0.0
e7+e5-e4              0.0
e8+e6-e5              0.0

e1+e4-(e2+e5)         0.0
e1+e4-(e3+e6)         0.0

e1+e7+e8-e3          -8.881784197001252e-16
e7+e8+e6-e4           0.0

i1-i7-i4             -5.551115123125783e-17
i6-i3-i8              6.938893903907228e-18
i2+i7-(i8+i5)         0.0
i1+i2+i3 - (i4+i5+i6) 0.0

Compute R

# Python code

E1 = e3+e6
I1 = i1 + i2 + i3
R1 = E1/I1
s1 = 'R1' ; print(s1,eval(s1))

E2 = e1 + e7 + e5
I2 = i4 + i5 + i6
R2 = E2/I2
s1 = 'R2' ; print(s1,eval(s1))

R1 21.973426856410605
R2 21.973426856410605

$R=R_{1}=R_{2}$

Solving big matrices

A big matrix is one of size greater than 10 by 11.

With each recursive call of solveMbyN() the size of each value in decimal digits can theoretically double. Python's integer math enjoys infinite precision. If your original matrix is of size 32 by 33, and each value in the matrix is an int of 1 decimal digit, function solve2by3() can be called with ints of size 2**30 (1,073,741,824) decimal digits.

Floats can be used instead of ints, but the limited precision of floats may not provide a desirable level of accuracy in the result.

Python's decimal objects are a good compromise and function reduceRow() above is an attempt to keep the size of each member manageable.

Function reduceRow() works well. However, as with all operations involving python's decimal objects, you need to pay careful attention to precision and accuracy of the results.

On my Mac the following python code generates a matrix of size 100 by 101 and calculates the result containing 100 values in about 1.5 seconds, including the time to generate 10,100 random numbers, each containing up to 12 decimal digits with the decimal point in a random position, and including the time to test output over 100 rows to verify that all calculated values of the solution satisfy each row.

In function solveMbyN() above find line:

if 0 : # For matrices greater than 10 by 11 enable this piece of code.

Change it to:

if 1 : # For matrices greater than 10 by 11 enable this piece of code.

Then:

from random import getrandbits
from decimal import *
import sys
getcontext().prec=50 # Set precision to 50.

numRows=100

def randomNumber():
# 1 invocation in 256 returns 0.
    if not (getrandbits(10) & 0xFF) : return Decimal(0)
    return [ w
             for q in [ getrandbits(10) & 1]
             for sign in [ (-1,1)[q] ]
             for numberOfDecimalPlaces in [ getrandbits(10) & 0xF ]
             for s1 in [ str(getrandbits(50))[-12:] ]
             for s2 in [ '0'*12+s1 ]
             for posn in [ len(s2)-numberOfDecimalPlaces ]
             for w in [ sign*Decimal(s2[:posn]+'.'+s2[posn:]) ]
           ][0]

data = [[ randomNumber() for p in range(numRows+1) ]
        for p in range (numRows)
       ]

datan = sorted([ v  for row in data for v in row if v < 0 ])
datap = sorted([ v  for row in data for v in row if v >= 0 ])
print ('A small sample of the random numbers in data:')
print ('+ve values:',len(datap), ',', datap[:2],'\n   ',datap[-2:])
print ('-ve values:',len(datan), ',', datan[:2],'\n   ',datan[-2:])

output = solveMbyN(data)

print ('A small sample of the solutions:')
print ('output[0]  =', output[0])
print ('output[19] =', output[19])
print ('output[59] =', output[59])
print ('output[99] =', output[99])

A small sample of the random numbers in data:
+ve values: 5021 , [Decimal('1.16871265E-7'), Decimal('1.73721245E-7')]
    [Decimal('998523464710'), Decimal('999768605679')]
-ve values: 5079 , [Decimal('-991079944209'), Decimal('-989786083110')]
    [Decimal('-4.10272824E-7'), Decimal('-2.38664537E-7')]
    
A small sample of the solutions:
output[0]  = 0.43689400018920695253771832432651757885163362928745
output[19] = 0.19867480862268284151047885891372314311902973127033
output[59] = 0.46169681824826309421940885550155275946668017604646
output[99] = -0.020598220802233733529683040085023443421113627790464

Testing results

Data input to function solveMbyN() is an array of 100 rows, each row containing 101 numbers.

[
[v0_0, v0_1, v0_2, ..... v0_98,v0_99,v0_100],
.......
[v99_0,v99_1,v99_2, ...... v99_98,v99_99,v99_100],]
]

Data received from function solveMbyN() is an array of 100 numbers.

[ s0,s1,s2, ...... s98,s99 ]

The first row is tested with the solutions by;

L2 = [ v0_0*s0, v0_1*s1, v0_2*s2, ..... v0_98*s98,v0_99*s99,v0_100 ]

sum is the sum of all items in L2.

sum is appended to L1 and the process is repeated for all 100 rows.

L1 = []
for row in data :
# a, b, c, d, e, f, g ....... # row
# u, v, w, x, y, z            # output
        L2 = [ row[p]*t1[p] for t1 in (output+(1,),) for p in range (0, len(row)) ]
# L2 = [a*u , b*v , c*w , d*x , e*y , f*z , g]
        sum = [ sum for sum in [0] for p in L2 for sum in [sum+p] ][-1]
# sum = [a*u, a*u + b*v, a*u + b*v + c*w, a*u + b*v + c*w + d*x, a*u + b*v + c*w + d*x + e*y,
#        a*u + b*v + c*w + d*x + e*y + f*z, a*u + b*v + c*w + d*x + e*y + f*z + g][-1]
# sum = a*u + b*v + c*w + d*x + e*y + f*z + g
# sum is the sum of all items in L2
        L1 += [abs(sum)]

L1a = sorted(L1)
print (len(L1a), L1a[0], L1a[-1])

Ideally sum should be zero.

In practice it's extremely unlikely that sum will be zero. My results typically gave values close to

100 4.1065149609E-38 9.6425614873452398368906E-25

The worst of the results above was 23 zeroes after the decimal point.

Better results can be achieved by increasing precision.

Cubic Resistive Network

**Figure 1. Diagram of resistive network containing 12 resistors.**
Blue arrows show assumed direction of current.

A resistive network containing 12 resistors is connected as shown in Figure 1.

The network is called "cubic" because, in 3 dimensions, each resistor is located on one edge of a cube.

What is resistance $R$ between points $P_{1},P_{2}?$

# Python code:

values_of_r = r1,r2,r3,r4,r5,r6,r7,r8,r9,r10,r11,r12 = 10,20,30,40,50,60,70,80,90,100,110,120

Solve for 12 Branch Currents

Create matrix 12 by 13

# Python code:
input = [
[10, 20, -30, -40,   0,  0,   0,   0,  0,    0,   0,    0,    0],  # e1 + e2 = e3 + e4
[ 0,  0,   0,   0,  50, 60, -70, -80,  0,    0,   0,    0,    0],  # e5 + e6 = e7 + e8
[ 0,  0,   0,  40,   0,  0,   0, -80,  0,    0, 110, -120,    0],  # e11 + e4 = e8 + e12
[10,  0,   0,   0, -50,  0,   0,   0, 90, -100,   0,    0,    0],  # e9 + e1 = e5 + e10
[ 0,  0,   0,   0,   1, -1,   0,   0,  0,   -1,   0,    0,    0],  # i5 = i10 + i6
[ 0,  0,   0,   0,   0,  0,   1,  -1,  0,    0,  -1,    0,    0],  # i7 = i11 + i8
[-1,  0,  -1,   0,   0,  0,   0,   0,  1,    0,   0,    0,    0],  # i9 = i1 + i3
[ 0,  0,  -1,   1,   0,  0,   0,   0,  0,    0,  -1,    0,    0],  # i4 = i3 + i11
[-1,  1,   0,   0,   0,  0,   0,   0,  0,   -1,   0,    0,    0],  # i2 = i1 + i10
[ 0,  0,   0,   0,   0, -1,   0,  -1,  0,    0,   0,    1,    0],  # i12 = i6 + i8
[ 0, -1,   0,  -1,   1,  0,   1,   0,  1,    0,   0,   -1,    0],  # i9 + i5 + i7 = i2 + i4 + i12
[ 0,  0,   1,   0,   0,  0,   0,   0,  0,    0,   0,    0, -1.6]  # i3 = 1.6
]

i1,i2,i3,i4,i5,i6,i7,i8,i9,i10,i11,i12 = values_of_i = solveMbyN (input)
s1 = 'values_of_i'
print(s1,eval(s1))

This matrix failed:

solve2by3() : empty row in input.
  input =
    (0, 0, 0)
    (90533116137774317568000000000000000000000000000000000000000000, -84449318308603494400000000000000000000000000000000000000000000, 1.4228848407261846e+61)
checkDirectionNumbers() : 2 rows parallel, 1 and 2.
  input of solve3by4() =
    [38760268800000000000000000000, 593753233920000000000000000000, -569385344000000000000000000000, 0]
    [620164300800000000000000000000000000, 9500051742720000000000000000000000000, -9110165504000000000000000000000000000, 0]
    [153839206400000000000000000000000, 20882470400000000000000000000000, -81126144000000000000000000000000, -3.67098806272e+32]

Try again

# Python code:
input = [
  [10, 20, -30, -40,   0,  0,   0,   0,  0,    0,   0,    0,    0],  # e1 + e2 = e3 + e4
  [ 0,  0,   0,   0,  50, 60, -70, -80,  0,    0,   0,    0,    0],  # e5 + e6 = e7 + e8
  [ 0,  0,   0,  40,   0,  0,   0, -80,  0,    0, 110, -120,    0],  # e11 + e4 = e8 + e12
  [10,  0,   0,   0, -50,  0,   0,   0, 90, -100,   0,    0,    0],  # e9 + e1 = e5 + e10
  [ 0,  0,   0,   0,   1, -1,   0,   0,  0,   -1,   0,    0,    0],  # i5 = i10 + i6
  [ 0,  0,   0,   0,   0,  0,   1,  -1,  0,    0,  -1,    0,    0],  # i7 = i11 + i8
  [-1,  0,  -1,   0,   0,  0,   0,   0,  1,    0,   0,    0,    0],  # i9 = i1 + i3
  [ 0,  0,  -1,   1,   0,  0,   0,   0,  0,    0,  -1,    0,    0],  # i4 = i3 + i11
  [-1,  1,   0,   0,   0,  0,   0,   0,  0,   -1,   0,    0,    0],  # i2 = i1 + i10
  [ 0,  0,   0,   0,   0, -1,   0,  -1,  0,    0,   0,    1,    0],  # i12 = i6 + i8
 #[ 0, -1,   0,  -1,   1,  0,   1,   0,  1,    0,   0,   -1,    0],  # i9 + i5 + i7 = i2 + i4 + i12 DELETED.
  [10, 20,   0,   0,   0,  0, -70, -80, 90,    0,   0, -120,    0],  # e9 + e1 + e2 = e7 + e8 + e12 ADDED.
  [ 0,  0,   1,   0,   0,  0,   0,   0,  0,    0,   0,    0, -1.6]   # i3 = 1.6
]

import decimal
dD = decimal.Decimal
dgt = decimal.getcontext()
Precision = dgt.prec = 30
Tolerance = dD("1e-" + str(Precision-2))

# Convert all values in input to decimal objects with precision of 30.

input = [ [ dD(str(p)) for p in v  ] for v in input ]

i1,i2,i3,i4,i5,i6,i7,i8,i9,i10,i11,i12 = values_of_i = solveMbyN (input)

# values_of_i

5.5027171492204899777282850777     9.3809275973899113038721525414     1.5999999999999999999999999999  # i3 should be 1.6.
4.8661430860000781463681475402     6.12901340210213730316883522816    2.25080295393271597702496776458
4.68526862814050716992927753670    1.41912554214042902356112999643    7.10271714922048997772828507766
3.87821044816942132614386746358    3.26614308600007814636814754027    3.66992849607314500058609776103

Compute R

# python code

values_of_e = e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12 = [ (i*r) for (i,r) in zip(values_of_i, values_of_r) ]

values_of_e
55.0271714922048997772828507770    187.618551947798226077443050828    47.9999999999999999999999999970 
194.645723440003125854725901608    306.450670105106865158441761408    135.048177235962958621498065875
327.968803969835501895049427569    113.530043371234321884890399714    639.244543429844097995545656989
387.821044816942132614386746358    359.275739460008596100496229430    440.391419528777400070331731324

$e_{3}$ should be $48,\ i_{3}*r_{3}$ or $1.6*30.$

E1 = e5 + e10 + e2
I1 = i9 + i5 + i7
R1 = E1/I1
s1 = 'R1' ; print(s1,eval(s1))

E2 = e7 + e8 - e6 + e10 - e1 + e3 + e4
I2 = i2 + i4 + i12
R2 = E2/I2
s1 = 'R2' ; print(s1,eval(s1))

R1 49.2208688540148837936367036806
R2 49.2208688540148837936367036803

Display results with precision of 28:

dgt.prec = 28
R1 += 0 ; R2 += 0
dgt.prec = Precision

s1 = 'R1' ; print(s1,eval(s1))
s1 = 'R2' ; print(s1,eval(s1))

R1 49.22086885401488379363670368 
R2 49.22086885401488379363670368

$R=R_{1}=R_{2}.$

Review

In matrix all values $i_{1},i_{2},\dots ,i_{11},i_{12}$ and $e_{1},e_{2},\dots ,e_{11},e_{12}$ are included.

Testing was done with the following lines substituted for last line of matrix:

# python code
[ 0,  0,   0,    0,   0,  0,   1,    0,  0,    0,   0,    0, -3.15]  # i7 = 3.15
[ 0,  0,   0,   r4,   0,  0,   0,    0,  0,    0,   0,    0, -6   ]  # e4 = 6
[ 0,  0,   r3,   0,   0,  0,   0,   r8,  0,    0,   0,    0, -5   ]  # e3 + e8 = 5

All tests produced a consistent value of $R.$

Checking

Examples of current nodes

$i_{1}+i_{10}=i_{2}$
$i_{6}+i_{8}=i_{12}$

Examples of voltage loops

Top and Bottom. $e_{1}+e_{2}-e_{4}-e_{3}=0$ $e_{5}+e_{6}-e_{8}-e_{7}=0$
Two sides in background. $e_{5}+e_{10}-e_{1}-e_{9}=0$ $e_{6}+e_{12}-e_{2}-e_{10}=0$
Two sides in foreground. $e_{7}+e_{11}-e_{3}-e_{9}=0$ $e_{8}+e_{12}-e_{4}-e_{11}=0$

Python code

t1 = (
# 3 nodes on top
'i1 + i10 - i2',
'i1 + i3 - i9',
'i3 + i11 - i4',

# 3 nodes on bottom
'i10 + i6 - i5',
'i11 + i8 - i7',
'i6 + i8 - i12',

# Total input current equals total output current.
'i5 + i7 + i9 - i2 - i4 - i12',

# Voltage loops
# top
'e1 + e2 - e4 - e3',

# bottom
'e5 + e6 - e8 - e7',

# 2 sides in background
'e9 + e1 - e10 - e5',
'e10 + e2 - e12 - e6',

# 2 sides in foreground
'e9 + e3 - e11 - e7',
'e11 + e4 - e12 - e8',

# Some elaborate loops.
'e8 - e6 + e10 + e2 - e4 - e3 - e9 + e7',
'e10 + e2 - e12 - e8 + e11 - e3 - e9 + e5',
)

Result of each of the above calculations should be $0.$

Because of small rounding errors, result may not be exactly $0.$

See values_of_i and values_of_e above.

This code verifies that result is close enough to $0$ to be acceptable.

For example:

${\text{result}}=e_{10}+e_{2}-e_{12}-e_{8}+e_{11}-e_{3}-e_{9}+e_{5}.$

${\text{v1}}=e_{10}+e_{2}+e_{11}+e_{5},$ sum of positive values.

${\text{status = (abs(result)}}<{\text{(v1}}*{\text{Tolerance)). status}}$ should be ${\text{True.}}$

# python code

import re

for str1 in t1 :
    str2 = re.sub ('\+', ';+', str1)
    str2 = re.sub ('\-', ';-', str2)
    L1 = str2.split(';')
    positives = ''.join([ v for v in L1 if '-' not in v ])
    result = eval(str1)
    v1 = eval( positives )
    status = (abs(result) < (v1*Tolerance))
    str3 = (str1+(' '*40))[:42]
    str4 = ((' '*10) + str(result))[-10:]
    str5 = '{}{}    {}'.format(str3,str4,status)
    print ( str5 )

Calculation	Result	Result Acceptable
$i_{1}+i_{10}-i_{2}$	$-1.2E-28$	${\text{True}}$
$i_{1}+i_{3}-i_{9}$	$-6E-29$	${\text{True}}$
$i_{3}+i_{11}-i_{4}$	$-3E-29$	${\text{True}}$
$i_{10}+i_{6}-i_{5}$	$0E-29$	${\text{True}}$
$i_{11}+i_{8}-i_{7}$	$0E-29$	${\text{True}}$
$i_{6}+i_{8}-i_{12}$	$-2E-29$	${\text{True}}$
$i_{5}+i_{7}+i_{9}-i_{2}-i_{4}-i_{12}$	$-3E-29$	${\text{True}}$
$e_{1}+e_{2}-e_{4}-e_{3}$	$0E-28$	${\text{True}}$
$e_{5}+e_{6}-e_{8}-e_{7}$	$0E-27$	${\text{True}}$
$e_{9}+e_{1}-e_{10}-e_{5}$	$0E-27$	${\text{True}}$
$e_{10}+e_{2}-e_{12}-e_{6}$	$-1.3E-26$	${\text{True}}$
$e_{9}+e_{3}-e_{11}-e_{7}$	$-1.3E-26$	${\text{True}}$
$e_{11}+e_{4}-e_{12}-e_{8}$	$0E-27$	${\text{True}}$
$e_{8}-e_{6}+e_{10}+e_{2}-e_{4}-e_{3}-e_{9}+e_{7}$	$0E-27$	${\text{True}}$
$e_{10}+e_{2}-e_{12}-e_{8}+e_{11}-e_{3}-e_{9}+e_{5}$	$0E-27$	${\text{True}}$

Big Matrix 64 by 65

A network containing 64 resistors is connected as shown in diagram.

What is resistance R between points P1, P2?

# python code
values_of_R = (
    R10, R11, R12, R13, R14, R15, R16, R17, R18, R19, 
    R20, R21, R22, R23, R24, R25, R26, R27, R28, R29, 
    R30, R31, R32, R33, R34, R35, R36, R37, R38, R39,
    R40, R41, R42, R43, R44, R45, R46, R47, R48, R49, 
    R50, R51, R52, R53, R54, R55, R56, R57, R58, R59, 
    R60, R61, R62, R63, R64, R65, R66, R67, R68, R69,
    R70, R71, R72, R73, 
) = [ v for v in range (100,731,10) ]

While this resistive circuit may be very theoretical, it lends itself well to the creation of a big matrix, 64 by 65, meaning that there are 64 resistors and 64 simultaneous equations to be solved.

Create matrix

An examination of the circuit produces the following conditions:

# python code

iconditions = [
              "+ i10 + i70 - i44" ,        "+ i11 - i10 - i49" ,        "+ i12 - i11 - i54",
              "+ i13 - i12 - i59" ,        "+ i14 - i13 - i64" ,        "+ i15 + i44 - i43",
  "+ i16 + i49 - i15 - i48 - i70" ,  "+ i17 + i54 - i16 - i53" ,  "+ i18 + i59 - i17 - i58",
  "+ i19 + i64 + i71 - i18 - i63" ,        "+ i69 - i19 - i68" ,        "+ i20 + i43 - i42",
        "+ i21 + i48 - i20 - i47" ,  "+ i22 + i53 - i21 - i52" ,  "+ i23 + i58 - i22 - i57",
        "+ i24 + i63 - i23 - i62" ,        "+ i68 - i24 - i67" ,        "+ i25 + i42 - i41",
        "+ i26 + i47 - i25 - i46" ,  "+ i27 + i52 - i26 - i51" ,  "+ i28 + i57 - i27 - i56",
        "+ i29 + i62 - i28 - i61" ,        "+ i67 - i29 - i66" ,        "+ i30 + i41 - i40",
  "+ i31 + i46 - i30 - i45 - i72" ,  "+ i32 + i51 - i31 - i50" ,  "+ i33 + i56 - i32 - i55",
  "+ i34 + i61 + i73 - i33 - i60" ,        "+ i66 - i34 - i65" ,        "+ i36 + i45 - i35",
              "+ i37 + i50 - i36" ,        "+ i38 + i55 - i37" ,        "+ i39 + i60 - i38",
              "+ i65 - i39 - i73"
]

sx = 'len(iconditions)' ; print (sx, '=', eval(sx))

len(iconditions) = 34

econditions = [
  "+ e40 + e30 - e35 - e45" ,  "+ e41 + e25 - e30 - e46" ,  "+ e42 + e20 - e25 - e47",
  "+ e43 + e15 - e20 - e48" ,  "+ e44 + e10 - e15 - e49" ,  "+ e45 + e31 - e36 - e50",
  "+ e46 + e26 - e31 - e51" ,  "+ e47 + e21 - e26 - e52" ,  "+ e48 + e16 - e21 - e53",
  "+ e49 + e11 - e16 - e54" ,  "+ e50 + e32 - e37 - e55" ,  "+ e51 + e27 - e32 - e56",
  "+ e52 + e22 - e27 - e57" ,  "+ e53 + e17 - e22 - e58" ,  "+ e54 + e12 - e17 - e59",
  "+ e55 + e33 - e38 - e60" ,  "+ e56 + e28 - e33 - e61" ,  "+ e57 + e23 - e28 - e62",
  "+ e58 + e18 - e23 - e63" ,  "+ e59 + e13 - e18 - e64" ,  "+ e60 + e34 - e39 - e65",
  "+ e61 + e29 - e34 - e66" ,  "+ e62 + e24 - e29 - e67" ,  "+ e63 + e19 - e24 - e68",
  "+ e64 + e14 - e19 - e69" ,        "+ e44 + e70 - e15" ,        "+ e64 + e14 - e71",
        "+ e40 + e30 - e72" ,        "+ e60 + e73 - e39"
]

sx = 'len(econditions)' ; print (sx, '=', eval(sx))

len(econditions) = 29

In iconditions and econditions there are 63 conditions that include all values of i and e. These 63 conditions are used to create matrix.

The 64th condition is added manually.

The matrix is:

matrix = [
  [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,],
  [-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,],
  [0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,1,0,0,0,],
  [0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,1,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,-1,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,300,0,0,0,0,-350,0,0,0,0,400,0,0,0,0,-450,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,250,0,0,0,0,-300,0,0,0,0,0,0,0,0,0,0,410,0,0,0,0,-460,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,200,0,0,0,0,-250,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,420,0,0,0,0,-470,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,150,0,0,0,0,-200,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,430,0,0,0,0,-480,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [100,0,0,0,0,-150,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,440,0,0,0,0,-490,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,310,0,0,0,0,-360,0,0,0,0,0,0,0,0,450,0,0,0,0,-500,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,260,0,0,0,0,-310,0,0,0,0,0,0,0,0,0,0,0,0,0,0,460,0,0,0,0,-510,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,210,0,0,0,0,-260,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,470,0,0,0,0,-520,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,160,0,0,0,0,-210,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,480,0,0,0,0,-530,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,110,0,0,0,0,-160,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,490,0,0,0,0,-540,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,320,0,0,0,0,-370,0,0,0,0,0,0,0,0,0,0,0,0,500,0,0,0,0,-550,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,270,0,0,0,0,-320,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,510,0,0,0,0,-560,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,220,0,0,0,0,-270,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,520,0,0,0,0,-570,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,170,0,0,0,0,-220,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,530,0,0,0,0,-580,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,120,0,0,0,0,-170,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,540,0,0,0,0,-590,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,330,0,0,0,0,-380,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,550,0,0,0,0,-600,0,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,280,0,0,0,0,-330,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,560,0,0,0,0,-610,0,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,230,0,0,0,0,-280,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,570,0,0,0,0,-620,0,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,180,0,0,0,0,-230,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,580,0,0,0,0,-630,0,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,130,0,0,0,0,-180,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,590,0,0,0,0,-640,0,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,340,0,0,0,0,-390,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,600,0,0,0,0,-650,0,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,290,0,0,0,0,-340,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,610,0,0,0,0,-660,0,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,240,0,0,0,0,-290,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,620,0,0,0,0,-670,0,0,0,0,0,0,0,],
  [0,0,0,0,0,0,0,0,0,190,0,0,0,0,-240,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,630,0,0,0,0,-680,0,0,0,0,0,0,],
  [0,0,0,0,140,0,0,0,0,-190,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,640,0,0,0,0,-690,0,0,0,0,0,],
  [0,0,0,0,0,-150,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,440,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,700,0,0,0,0,],
  [0,0,0,0,140,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,640,0,0,0,0,0,0,-710,0,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,300,0,0,0,0,0,0,0,0,0,400,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-720,0,0,],
  [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-390,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,600,0,0,0,0,0,0,0,0,0,0,0,0,730,0,],
  [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1,],
]

sx = 'len(matrix)' ; print (sx, '=', eval(sx))

len(matrix) = 64

Bottom line of matrix is equivalent to: $(1)i10+(-1)=0$ or $i10=1.$

First result

The following conditions are included for testing:

more_econditions = [
  "+ e49 + e70 - e10",
  "+ e19 + e69 - e71",
  "+ e35 + e45 - e72",
  "+ e65 + e73 - e34",
] 

extra_test_conditions = [
  "+ e40 + e41 + e42 + e43 + e44 + e10 - e35 - e45 - e46 - e47 - e48 - e49",
  "+ e45 + e46 + e47 + e48 + e49 + e11 - e36 - e50 - e51 - e52 - e53 - e54",
  "+ e50 + e51 + e52 + e53 + e54 + e12 - e37 - e55 - e56 - e57 - e58 - e59",
  "+ e55 + e56 + e57 + e58 + e59 + e13 - e38 - e60 - e61 - e62 - e63 - e64",
  "+ e60 + e61 + e62 + e63 + e64 + e14 - e39 - e65 - e66 - e67 - e68 - e69",
  "+ e44 + e10 + e11 + e12 + e13 + e14 - e69 - e15 - e16 - e17 - e18 - e19",
  "+ e43 + e15 + e16 + e17 + e18 + e19 - e68 - e20 - e21 - e22 - e23 - e24",
  "+ e42 + e20 + e21 + e22 + e23 + e24 - e67 - e25 - e26 - e27 - e28 - e29",
  "+ e41 + e25 + e26 + e27 + e28 + e29 - e66 - e30 - e31 - e32 - e33 - e34",
  "+ e40 + e30 + e31 + e32 + e33 + e34 - e65 - e35 - e36 - e37 - e38 - e39",
  "+ i35 + i40 + i72 - i14 - i69 - i71",
  "+ e40 + e41 + e42 + e43 + e44 + e10 + e11 + e12 + e13 + e14 - e35 - e36 - e37 - e38 - e39 - e65 - e66 - e67 - e68 - e69",
  "+ e40 + e41 + e42 + e43 + e15 + e16 + e17 + e18 + e19 + e69 - e35 - e36 - e37 - e38 - e60 - e61 - e62 - e63 - e64 - e14",
  "+ e40 + e41 + e42 + e20 + e21 + e22 + e23 + e24 + e68 + e69 - e35 - e36 - e37 - e55 - e56 - e57 - e58 - e59 - e13 - e14",
  "+ e40 + e41 + e25 + e26 + e27 + e28 + e29 + e67 + e68 + e69 - e35 - e36 - e50 - e51 - e52 - e53 - e54 - e12 - e13 - e14",
  "+ e40 + e30 + e31 + e32 + e33 + e34 + e66 + e67 + e68 + e69 - e35 - e45 - e46 - e47 - e48 - e49 - e11 - e12 - e13 - e14"
]

Produce results:

if 1 :
    import decimal
    dD = decimal.Decimal
    dgt = decimal.getcontext()
    Precision = dgt.prec = 60                   # Adjust as necessary.
    Tolerance = dD("1e-" + str(Precision-4))    # Adjust as necessary.
    
    import re # Regular expressions.

def produce_result (input, flag = 0) :
    thisName = 'produce_result (input, flag = {}) :'.format(flag)

    values_of_i = solveMbyN (input)

    (   i10, i11, i12, i13, i14, i15, i16, i17, i18, i19, 
        i20, i21, i22, i23, i24, i25, i26, i27, i28, i29, 
        i30, i31, i32, i33, i34, i35, i36, i37, i38, i39,
        i40, i41, i42, i43, i44, i45, i46, i47, i48, i49, 
        i50, i51, i52, i53, i54, i55, i56, i57, i58, i59, 
        i60, i61, i62, i63, i64, i65, i66, i67, i68, i69,
        i70, i71, i72, i73, 
    ) = values_of_i

    values_of_e = (
        e10, e11, e12, e13, e14, e15, e16, e17, e18, e19, 
        e20, e21, e22, e23, e24, e25, e26, e27, e28, e29, 
        e30, e31, e32, e33, e34, e35, e36, e37, e38, e39,
        e40, e41, e42, e43, e44, e45, e46, e47, e48, e49, 
        e50, e51, e52, e53, e54, e55, e56, e57, e58, e59, 
        e60, e61, e62, e63, e64, e65, e66, e67, e68, e69,
        e70, e71, e72, e73, 
    ) = [ (i*R) for (i,R) in zip (values_of_i, values_of_R) ]

    E1_ = 'e40 + e41 + e42 + e43 + e44 + e10 + e11 + e12 + e13 + e14'
    E1 = eval(E1_)
    I1 = eval('i40 + i72 + i35')
    R1 = E1/I1

    if not flag : return R1
    # Check all conditions.
    # compiled regular expression plus, compiled regular expression minus
    crep,crem = [ re.compile(re.escape(v)) for v in '+-' ]
    # 
    # This code verifies that result of evaluation of condition 
    # is close enough to 0 to be called 0.
    # 
    for condition in (iconditions + econditions + more_econditions + extra_test_conditions):
        str2 = crep.sub(';+', condition)
        str3 = crem.sub(';-', str2)
        positives = [ v for v in str3.split(';') if ('+' in v) ]
        pos_sum = eval(''.join(positives))
        sum = eval(condition)
        # pos_sum - neg_sum = sum
        neg_sum = pos_sum - sum
        min,max = sorted((neg_sum, pos_sum))
        status = (abs(sum) <= (Tolerance*min))
        if not status :
            print (thisName, 'condition failed:')
            print ('   ', condition, sum)
            return None

    return R1

# Convert all values in matrix to Decimal objects
matrix = [ [ dD(str(eval(str(p)))) for p in v  ] for v in matrix ]

enable_reduceRow = 1

R = produce_result (matrix,1) 

sx = 'R' ; print (sx, '=', eval(sx))

R = 723.928575988442547699732563335265663515838075102937503680598

${\text{R}}$ is printed with precision of 60.

Matrix corrected

Original assumptions were that currrent flow through 64 resistors would be from bottom to top or from left to right.

Examination of results shows that flow through R70, R73 is from right to left. This is reflected in testing below.

Corrected diagram conforms to assumption that all current flow is from bottom towards top or from left to right.

number_of_columns = 65
output = []
# 
# Test this matrix 64 times using 
# i10 = 1
# i11 = 1.1
# i12 = 1.2
# .......
# .......
# i70 = -7
# i71 = 7.1
# i72 = 7.2
# i73 = -7.3
# 
for I in range(10, 74):
    new_line = [ dD(0) ] * number_of_columns
    place_in_line = I - 10
    new_line[place_in_line] = dD(1)
    i = dD(I)/10
    if I in (70,73) : new_line[-1] = i
    else : new_line[-1] = -i
    matrix[-1] = new_line
    r = produce_result (matrix,1)
    if r : output += [ r ]
    
sx = 'len(output)' ; print (sx, '=', eval(sx))

# Produce results with slightly reduced precision:

dgt.prec -= 4
set2 = { r+0 for r in output }
dgt.prec += 4
    
len2 = len(set2)
if len2 == 1 :
    r, = set2
    print ('R =', r)
else :
    print (len2, 'values of R:')
    for v in set2 : print ('   ', v)

len(output) = 64 
R = 723.92857598844254769973256333526566351583807510293750368

${\text{R}}$ is printed with precision of 56.

With precision of 56 all 64 results are equal.