Translations:

HansVanLeunen respectfully asks that people use the discussion page, their talk page or email them, rather than contribute to this page at this time. This page might be under construction, controversial, used currently as part of a brick and mortar class by a teacher, or document an ongoing research project. Please RESPECT their wishes by not editing this page.

Information Messengers

Warp strings

Warps are a type of solutions of the homogeneous second order partial differential equations. We take the equation that does not apply the d'Alembert's operator.

$(\nabla _{r}\nabla _{r}+\langle {\vec {\nabla }},{\vec {\nabla }}\rangle )\psi =0$

Between the solutions of this equation occur one-dimensional shock fronts that we call warps. One time actuators that operate in a single dimension emit these shock fronts.

${\vec {\psi }}=f_{r}(c\tau -{\vec {r}})\,{\vec {i}}$

The real scalar $c$ equals the speed at which the shock front travels. The vector ${\vec {r}}$ is the distance from the trigger location to the shock front.

Vector ${\vec {i}}$ represents the amplitude of the front, which directs perpendicular to ${\vec {r}}$ .

The function $f_{r}(q)$ is a real function that describes the shape of the front in the direction of ${\vec {r}}$ .

Warps do not feature a frequency. However, warps carry a standard bit of energy. That bit of energy can also be interpreted as a bit of information.

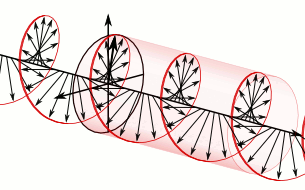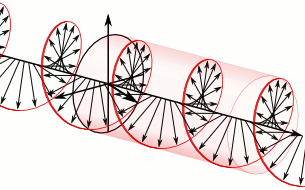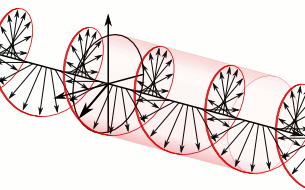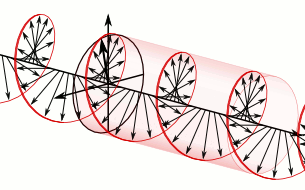
Warps may occur as isolated objects, but warps can also occur equidistant in strings.

In the string the direction of vector ${\vec {i}}$ may rotate as a function of the sequence number of the warp. This gives the string a circular polarization.

Circular polarization of warp string. The arrows represent the amplitudes of the warps that constitute the string. The red line is a help line. No wave is involved!

Circular polarization may occur right-handed or left-handed. If no rotation occurs then the polarization is linear. The actuator determines the kind of polarization.

The behavior of the warp strings invites their interpretation as information messengers.

Messengers

Interpretation

Photons can travel over huge distances in a path that crosses "empty space". Conventional physics interprets photons as waves of an electromagnetic field. Waves can only do this inside a wave guide. Empty space does not provide such wave guides. Thus waves cannot represent photons. Unguided waves spread in all directions. In this way their amplitude quickly diminishes to negligible values. Waves cannot travel billions of light years and still have sufficient energy left in order to be detected by a relatively small photon detector.

In addition, the EM field relies on the nearby existence of electric charges. The amplitude of electric fields diminishes quickly with increasing distance from electric charges. Thus, the electromagnetic field is no suitable carrier for long range information transport. It cannot possibly form a field that stretches uniformly over a billion light years.

The notion of warp strings as information messenger differs fundamentally from the current mainstream physical interpretation of a photon.

The Hilbert Book Model interprets warp strings that take part in long range information transfer as vibrations of the Palestra, which is the field that embeds and gets deformed by massive particles. As information messengers, the warp strings can perform in combination with the Palestra the trick that is observed from photons.

Information transfer

Photons are information messengers that are constituted of solutions of the homogeneous second order partial differential equations. These solutions represent warps.

Warps are one-dimensional shock fronts. These fronts keep their amplitude when they move.

Warps can cross huge spatial distances without losing their integrity. Warps move with a constant speed that is determined by its carrying field. This carrying field is the Palestra.

Warps appear equidistant in strings that are emitted by atomic modular systems. The atomic modular systems can also absorb messengers of that same frequency.

In fact the atomic modular systems can emit and absorb a complete signature of frequencies. That signature is characteristic for the type of atomic modular system.

Photons can also be emitted when an elementary module annihilates its antiparticle.

Locally and independent of the frequency, the duration of the emission of photons equals the duration of the absorption and the value is a constant.

All photons obey the Einstein-Planck relation. $E=h\,\nu$ .The energy of this information messenger is proportional to its frequency. This means that locally, all messenger strings feature a constant spatial length. This does not mean that after a travel over a very long range, the duration of the absorption is still equal to the duration of the emission.

In fact, Hubble's law tells otherwise. Due to expansion of the Palestra with the increase of progression, the distance between the warps increases. Thus, the spatial frequency decreases. At the same time the spatial length of the photon increases. Therefore the energy of the expanded photon stays the same. If the speed of the warps stays the same, then after a long trip the duration of the passage of the photon will take longer.

Consequence off Einstein-Planck relation

The consequence of the Einstein-Planck relation is that locally the duration of emission, passage and absorption are constant, but this also means that the regeneration duration of the elementary module equals that same constant.

At the annihilation of an elementary module, information messengers are produced. The duration of the generation of these warp strings must equal the standard local duration for messenger emission. But that duration is also equal to the duration of the regeneration cycle of the complete swarm. This conclusion means that all regeneration cycles of elementary modules must be equal, or several types of warp strings must exist such that each type of elementary particle corresponds to a type of warp string. The regeneration cycle period determines the mass of the elementary module. Different mass for different elementary module types means different regeneration cycle periods.

This deliberation leads to the following conclusion. If different types of elementary modules possess different mass, then each elementary module type that owns a unique mass corresponds to a different type of warp string. Another consequence is that Hubble's law involves that also the duration of the regeneration cycle of elementary particles changes with progression.

The absorption dilemma

The emission process of photons already raises eyebrows. During the emission process, the platform of the module that emits the photon must not move in lateral direction, otherwise the source cannot produce a one-dimensional string of warps.

Absorption requests an incredible aiming precision. Also here, during the absorption, the target must not move in lateral direction. In fact, absorption can better be comprehended in the creator's view as a reverse emission process. For observers the absorption stays incomprehensible. This indicates that absorption and emission can be described by a procedure that applies the creator's view.

Emission and absorption of strings of warps result from mode changes of the stochastic process, which generates the locations of the footprint of the source or target module. The basic mode of the module means that the module's platform moves uniformly. In addition the module oscillates at its lowest level mode. In atomic modules the Helmholtz equation describes these oscillation modes. A change of the oscillation mode as well as a change of platform speed causes the emission or absorption of strings of warps. During the mode-change procedure the platform stays at the same location in the background parameter space. At that location the warps depart or arrive. The warp string is one-dimensional.

Thus the source or target locates at the geometric center of the platform on which the module resides. This center also represents the location of the symmetry related charge of the module.

The duration of all photons is independent of their frequency. This also holds for photons that appear at annihilation events. That duration equals the regeneration cycle of the swarm. Thus, atoms emit and absorb the photon during that same duration. Here, the difference in mass between elementary particle types poses a dilemma. This suggests that different types of photons accompany different types of elementary particles. Either the duration differs or the energy of the warps differ.

A similar situation occurs with the explanation of the zigzag of elementary particles. There the absorption of photons must also be explained as a time-reversed emission process.

Photons versus waves

Photons are not waves, but like the fact that photons imitate waves by providing a frequency can waves imitate the behavior of photons. However, in this case the wave must live in a wave guide. The wave guide must ensure that the wave behaves a a one-dimensional object. Often radio waves are considered to be a particular kind of photon. This is faulty reasoning. The antenna shapes wave packages such that over a long trajectory the wave package behaves as a one-dimensional vibration. Moving wave packages disperse. Thus without a more efficient wave guide the waves go their own way and spread in all directions.

If the emitter spreads photons (or warps) in an angular distribution, then the photons (or warps) start to simulate the behavior of waves. In fact the location density distribution of the warps will act as a probability wave. This probability wave must be distinguished from the waves that are vibrations of the carrier field. In case of radio waves the carrier field is an electromagnetic field. The carrier field of photons is the embedding field. Only the embedding field can transport warps over huge distances. The two fields differ fundamentally.

All basic fields support the same second order partial differential equations. The actuators determine which solutions will be activated. Further, the boundary conditions determine which solutions sustain.