Full octahedral group

The full octahedral group O_h is the hyperoctahedral group of dimension 3. This article mainly looks at it as the symmetry group of the cube.

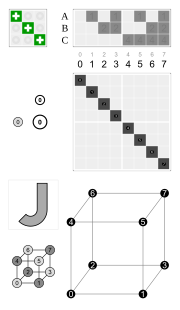
There are A000165(3) = 48 permutation of the cube. Half of them are its rotations, forming the subgroup O (the symmetric group S₄), and the other half are their inversions.
The inversion is the permutation that exchanges opposite vertices of the cube. It is not to be confused with the inversion of a permutation.

Conjugacy classes
Elements of O			Inversions of elements of O
identity	neut	0	inversion	inv3	0'
3 × rotation by 180° about a 4-fold axis	inv2	7, 16, 23	3 × reflection in a plane perpendicular to a 4-fold axis	ref1	7', 16', 23'
8 × rotation by 120° about a 3-fold axis	rot3	3, 4, 8, 11, 12, 15, 19, 20	8 × rotoreflection by 60°	rotref3	3', 4', 8', 11', 12', 15', 19', 20'
6 × rotation by 180° about a 2-fold axis	rot2	1', 2', 5', 6', 14', 21'	6 × reflection in a plane perpendicular to a 2-fold axis	ref2	1, 2, 5, 6, 14, 21
6 × rotation by 90° about a 4-fold axis	rot1	9', 10', 13', 17', 18', 22'	6 × rotoreflection by 90°	rotref1	9, 10, 13, 17, 18, 22

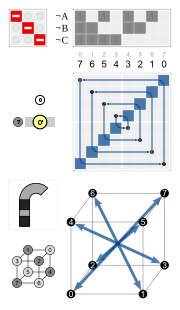
Examples
$(0,0)=0$	$(3,0)=7$	$(0,3)=3$	$(7,1)=1'$	$(4,5)=9'$
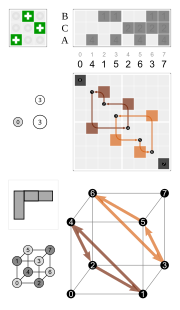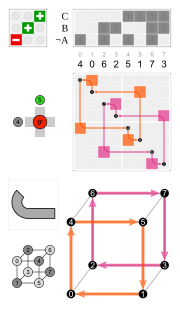neut	inv2	rot3	rot2	rot1
inv3	ref1	rotref3	ref2	rotref1
$(7,0)=0'$	$(4,0)=7'$	$(7,3)=3'$	$(0,1)=1$	$(3,5)=9$
See full list below: 8×6 matrix or Conjugacy classes

As the hyperoctahedral group of dimension 3 the full octahedral group is the wreath product $S_{2}\wr S_{3}\simeq S_{2}^{3}\rtimes S_{3}$ ,
and a natural way to identify its elements is as pairs $(m,n)$ with $m\in [0,2^{3})$ and $n\in [0,3!)$ .
But as it is also the direct product $S_{4}\times S_{2}$ , one can simply identify the elements of tetrahedral subgrup T_d as $a\in [0,4!)$ and their inversions as $a'$ .

So e.g. the identity $(0,0)$ is represented as $0$ and the inversion $(7,0)$ as $0'$ .
$(3,1)$ is represented as $6$ and $(4,1)$ as $6'$ .

A rotoreflection is a combination of rotation and reflection.
While a rotation leaves its axis and a reflection leaves its plane unchanged, a rotoreflection leaves only the center unchanged.

Illustration of rotoreflections
The reflection $7'$ applied on the 120° rotation $4$ gives the 60° rotoreflection $8'$ . $7'\circ 4=8'$
The reflection $7'$ applied on the 90° rotation $22'$ gives the 90° rotoreflection $17$ . $7'\circ 22'=17$

Cayley table

As there are two ways to denote the elements of this group, there are two ways to write the Cayley table.

S₄

The easier one is that in S₄ based notation: It simply doubles the Cayley table of S₄.
With $a,b,c\in S_{4}$ and $a',b',c'$ being their respective inversions, $a\circ b=c$ implies $a'\circ b'=c$ and $a\circ b'=a'\circ b=c'$ .

Example: $12'\circ 21=18'$

pairs

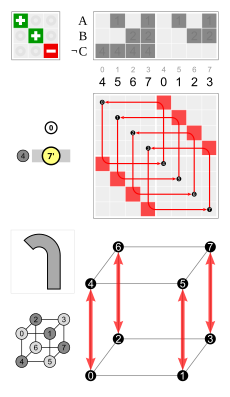
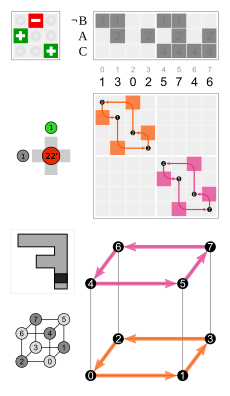
The notation with pairs is probably more useful, but also more complicated:

(pm,pn)=(am,an)\circ (bm,bn)

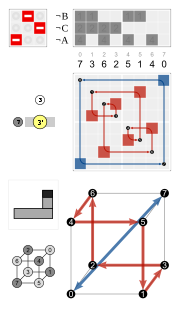
The calculation of $pm$ involves the cube vertex permutation shown in the images. E.g. $\mathrm {cvp} (2,3)=(2,6,3,7,~0,4,1,5)$ .

pm=\mathrm {cvp} (am,an)[bm]

$pn$ simply follows from the Cayley table of S₃:

pn=an\circ bn

Example: $(pm,pn)=(2,3)\circ (6,2)$

pm=\mathrm {cvp} (2,3)[6]=1

pn=3\circ 2=5

example


$12'$	$\circ$	$21$	$=$	$18'$
$(2,3)$	$\circ$	$(6,2)$	$=$	$(1,5)$

Overview

Truncated cuboctahedron

The vertices of the truncated cuboctahedron correspond to the elements of this group. Each of its faces of its dual, the disdyakis dodecahedron, is a fundamental domain.

8×6 matrix

truncated cuboctahedron

number matrices

S₄ based identifiers

0	1	2	3	4	5
23'	22'	21'	20'	19'	18'
16'	17'	13'	12'	15'	14'
7	6	10	11	8	9
7'	6'	10'	11'	8'	9'
16	17	13	12	15	14
23	22	21	20	19	18
0'	1'	2'	3'	4'	5'

Reverse colexicographic ranks

0	722	288	2210	1032	2354
5167	6490	5455	7978	6936	8258
11536	10213	12096	14018	10615	13738
16703	15981	17263	19786	16519	19642
23616	24338	23056	20533	23800	20677
28783	30106	28223	26301	29704	26581
35152	33829	34864	32341	33383	32061
40319	39597	40031	38109	39287	37965

Inversion numbers

0	2	4	6	6	8
4	6	8	10	10	12
8	6	12	14	10	12
12	10	16	18	14	16
16	18	12	10	14	12
20	22	16	14	18	16
24	22	20	18	18	16
28	26	24	22	22	20

Left inversion counts

00000000	00100010	00002200	00102030	00003210	00103130
01010101	00210021	01012301	00212041	00004321	00104241
00220022	01020102	00004422	00104252	01012402	00212052
01230123	01130113	01014523	00214263	01013513	00213163
00004444	00104454	00220044	01020304	00221054	01021404
01014545	00214465	01230145	01130315	00222165	01022515
00224466	01024546	00222266	01022526	01230246	01130326
01234567	01134557	01232367	01132537	01231357	01131437

It can be seen that the reverse colexicographic ranks of two inversions (in the sense of point reflections) add up to 40319 - the rank of the inversion (in the sense of point reflection) itself.
This means that their inversion sets (sets of pairs out of their natural order) are complements. (Beware the two different meanings of inversion here.)

Hexagon corresponding to top matrix row

3D diagrams

The files below illustrate the subgroup C_3v or [3] that corresponds to the top matrix row. It contains the six permutations of the cube that leave the main diagonal fixed.

permutohedron coordinates	permutohedron	Cayley graph generated by and	Cayley graph generated by and
example solid

2D equivalents

The rest of this article uses left action, i.e. $f\cdot g$ means first $g$ , then $f$ ,
but these two-dimensional diagrams use right action, i.e. $f\cdot g$ means first $f$ , then $g$ .
So ${\color {RoyalBlue}a}~{\widehat {=}}$ and ${\color {RubineRed}r}~{\widehat {=}}$ , but ${\color {RoyalBlue}a}\cdot {\color {RubineRed}r}~{\widehat {=}}$ $\cdot$ $=$ and ${\color {RubineRed}r}\cdot {\color {RoyalBlue}a}~{\widehat {=}}$ $\cdot$ $=$ .

details

This is left action again, so the 3×3 permutation matrices shown here are the transposes of those in the small permutohedron in the box above - which only makes a difference for

and

.

Cubes corresponding to matrix columns

Each of the six cubes in the following collapsible boxes shows one of the basic permutations from the top row of the matrix in the bottom left position.
In the other seven positions are the products of applying the reflections along coordinate axes on these basic permutations.

cube

truncated cuboctahedron

cube

truncated cuboctahedron

cube

truncated cuboctahedron

cube

truncated cuboctahedron

cube

truncated cuboctahedron

cube

truncated cuboctahedron

Conjugacy classes

The full octahedral group has A000712(3) = 10 conjugacy classes.

Two permutations $(m,n)$ and $(k,n)$ are complementary to each other, if $m+k=7$ .
Complementary permutations sum up to a vector of 7s, and their inversion sets are complements,
so their inversion numbers sum up to 28. (Compare one of the number matrices above.)

The conjugacy classes below are always shown in complementary pairs (like inv2/ref1 or rot2/ref2).
The numbers over the triangles are the inversion numbers of the corresponding permutations. It can be seen that corresponding numbers add up to 28.

neut (1)	inv3 (1)	inv2 (3)	ref1 (3)	rot3 (8)	rotref3 (8)	rot2 (6)	ref2 (6)	rot1 (6)	rotref1 (6)

neut (1 × 1)	inv3 (1 × 1)
0	28

inv2 (3 × 1)			ref1 (3 × 1)
12	20	24	16	8	4

rot3 (4 × 2)
6		14		18		18

rotref3 (4 × 2)
22		14		10		10

rot2 (6 × 1)
26	18	20	12	24	8

ref2 (6 × 1)
2	10	8	16	4	20

rot1 (3 × 2)						rotref1 (3 × 2)
6		12		12		22		16		16

Conjugacy classes of square permutations
neut	inv2	ref1		ref2		rot1
0	6	2	4	1	5	3

Examples for tesseract and penteract

The respective numbers of conjugacy classes for 4 and 5 dimensions are 20 and 36.
The following dictionaries show an example pair and the corresponding permutation from each conjugacy class.
(See here for the whole tesseract group.)

examples4 = {
    (0, 0): (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15),
    (0, 1): (0, 1, 2, 3, 8, 9, 10, 11, 4, 5, 6, 7, 12, 13, 14, 15),
    (0, 3): (0, 1, 4, 5, 8, 9, 12, 13, 2, 3, 6, 7, 10, 11, 14, 15),
    (0, 7): (0, 2, 1, 3, 8, 10, 9, 11, 4, 6, 5, 7, 12, 14, 13, 15),
    (0, 9): (0, 2, 4, 6, 8, 10, 12, 14, 1, 3, 5, 7, 9, 11, 13, 15),
    (1, 0): (1, 0, 3, 2, 5, 4, 7, 6, 9, 8, 11, 10, 13, 12, 15, 14),
    (1, 1): (1, 3, 0, 2, 5, 7, 4, 6, 9, 11, 8, 10, 13, 15, 12, 14),
    (1, 2): (1, 0, 3, 2, 9, 8, 11, 10, 5, 4, 7, 6, 13, 12, 15, 14),
    (1, 3): (1, 3, 5, 7, 0, 2, 4, 6, 9, 11, 13, 15, 8, 10, 12, 14),
    (1, 7): (1, 3, 0, 2, 9, 11, 8, 10, 5, 7, 4, 6, 13, 15, 12, 14),
    (1, 8): (1, 0, 5, 4, 9, 8, 13, 12, 3, 2, 7, 6, 11, 10, 15, 14),
    (1, 9): (1, 3, 5, 7, 9, 11, 13, 15, 0, 2, 4, 6, 8, 10, 12, 14),
    (3, 0): (3, 2, 1, 0, 7, 6, 5, 4, 11, 10, 9, 8, 15, 14, 13, 12),
    (3, 2): (3, 2, 7, 6, 1, 0, 5, 4, 11, 10, 15, 14, 9, 8, 13, 12),
    (3, 6): (3, 2, 1, 0, 11, 10, 9, 8, 7, 6, 5, 4, 15, 14, 13, 12),
    (3, 8): (3, 2, 7, 6, 11, 10, 15, 14, 1, 0, 5, 4, 9, 8, 13, 12),
    (3, 16): (3, 7, 11, 15, 2, 6, 10, 14, 1, 5, 9, 13, 0, 4, 8, 12),
    (7, 0): (7, 6, 5, 4, 3, 2, 1, 0, 15, 14, 13, 12, 11, 10, 9, 8),
    (7, 6): (7, 6, 5, 4, 15, 14, 13, 12, 3, 2, 1, 0, 11, 10, 9, 8),
    (15, 0): (15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0)
}

examples5 = {
    (0, 0): (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31),
    (0, 1): (0, 1, 2, 3, 4, 5, 6, 7, 16, 17, 18, 19, 20, 21, 22, 23, 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, 28, 29, 30, 31),
    (0, 3): (0, 1, 2, 3, 8, 9, 10, 11, 16, 17, 18, 19, 24, 25, 26, 27, 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, 28, 29, 30, 31),
    (0, 7): (0, 1, 4, 5, 2, 3, 6, 7, 16, 17, 20, 21, 18, 19, 22, 23, 8, 9, 12, 13, 10, 11, 14, 15, 24, 25, 28, 29, 26, 27, 30, 31),
    (0, 9): (0, 1, 4, 5, 8, 9, 12, 13, 16, 17, 20, 21, 24, 25, 28, 29, 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27, 30, 31),
    (0, 27): (0, 2, 1, 3, 8, 10, 9, 11, 16, 18, 17, 19, 24, 26, 25, 27, 4, 6, 5, 7, 12, 14, 13, 15, 20, 22, 21, 23, 28, 30, 29, 31),
    (0, 33): (0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31),
    (1, 0): (1, 0, 3, 2, 5, 4, 7, 6, 9, 8, 11, 10, 13, 12, 15, 14, 17, 16, 19, 18, 21, 20, 23, 22, 25, 24, 27, 26, 29, 28, 31, 30),
    (1, 1): (1, 3, 0, 2, 5, 7, 4, 6, 9, 11, 8, 10, 13, 15, 12, 14, 17, 19, 16, 18, 21, 23, 20, 22, 25, 27, 24, 26, 29, 31, 28, 30),
    (1, 2): (1, 0, 3, 2, 5, 4, 7, 6, 17, 16, 19, 18, 21, 20, 23, 22, 9, 8, 11, 10, 13, 12, 15, 14, 25, 24, 27, 26, 29, 28, 31, 30),
    (1, 3): (1, 3, 5, 7, 0, 2, 4, 6, 9, 11, 13, 15, 8, 10, 12, 14, 17, 19, 21, 23, 16, 18, 20, 22, 25, 27, 29, 31, 24, 26, 28, 30),
    (1, 7): (1, 3, 0, 2, 5, 7, 4, 6, 17, 19, 16, 18, 21, 23, 20, 22, 9, 11, 8, 10, 13, 15, 12, 14, 25, 27, 24, 26, 29, 31, 28, 30),
    (1, 8): (1, 0, 3, 2, 9, 8, 11, 10, 17, 16, 19, 18, 25, 24, 27, 26, 5, 4, 7, 6, 13, 12, 15, 14, 21, 20, 23, 22, 29, 28, 31, 30),
    (1, 9): (1, 3, 5, 7, 9, 11, 13, 15, 0, 2, 4, 6, 8, 10, 12, 14, 17, 19, 21, 23, 25, 27, 29, 31, 16, 18, 20, 22, 24, 26, 28, 30),
    (1, 26): (1, 0, 5, 4, 3, 2, 7, 6, 17, 16, 21, 20, 19, 18, 23, 22, 9, 8, 13, 12, 11, 10, 15, 14, 25, 24, 29, 28, 27, 26, 31, 30),
    (1, 27): (1, 3, 5, 7, 0, 2, 4, 6, 17, 19, 21, 23, 16, 18, 20, 22, 9, 11, 13, 15, 8, 10, 12, 14, 25, 27, 29, 31, 24, 26, 28, 30),
    (1, 31): (1, 3, 0, 2, 9, 11, 8, 10, 17, 19, 16, 18, 25, 27, 24, 26, 5, 7, 4, 6, 13, 15, 12, 14, 21, 23, 20, 22, 29, 31, 28, 30),
    (1, 32): (1, 0, 5, 4, 9, 8, 13, 12, 17, 16, 21, 20, 25, 24, 29, 28, 3, 2, 7, 6, 11, 10, 15, 14, 19, 18, 23, 22, 27, 26, 31, 30),
    (1, 33): (1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30),
    (3, 0): (3, 2, 1, 0, 7, 6, 5, 4, 11, 10, 9, 8, 15, 14, 13, 12, 19, 18, 17, 16, 23, 22, 21, 20, 27, 26, 25, 24, 31, 30, 29, 28),
    (3, 2): (3, 2, 7, 6, 1, 0, 5, 4, 11, 10, 15, 14, 9, 8, 13, 12, 19, 18, 23, 22, 17, 16, 21, 20, 27, 26, 31, 30, 25, 24, 29, 28),
    (3, 6): (3, 2, 1, 0, 7, 6, 5, 4, 19, 18, 17, 16, 23, 22, 21, 20, 11, 10, 9, 8, 15, 14, 13, 12, 27, 26, 25, 24, 31, 30, 29, 28),
    (3, 8): (3, 2, 7, 6, 11, 10, 15, 14, 1, 0, 5, 4, 9, 8, 13, 12, 19, 18, 23, 22, 27, 26, 31, 30, 17, 16, 21, 20, 25, 24, 29, 28),
    (3, 16): (3, 7, 11, 15, 2, 6, 10, 14, 1, 5, 9, 13, 0, 4, 8, 12, 19, 23, 27, 31, 18, 22, 26, 30, 17, 21, 25, 29, 16, 20, 24, 28),
    (3, 26): (3, 2, 7, 6, 1, 0, 5, 4, 19, 18, 23, 22, 17, 16, 21, 20, 11, 10, 15, 14, 9, 8, 13, 12, 27, 26, 31, 30, 25, 24, 29, 28),
    (3, 30): (3, 2, 1, 0, 11, 10, 9, 8, 19, 18, 17, 16, 27, 26, 25, 24, 7, 6, 5, 4, 15, 14, 13, 12, 23, 22, 21, 20, 31, 30, 29, 28),
    (3, 32): (3, 2, 7, 6, 11, 10, 15, 14, 19, 18, 23, 22, 27, 26, 31, 30, 1, 0, 5, 4, 9, 8, 13, 12, 17, 16, 21, 20, 25, 24, 29, 28),
    (3, 40): (3, 7, 11, 15, 2, 6, 10, 14, 19, 23, 27, 31, 18, 22, 26, 30, 1, 5, 9, 13, 0, 4, 8, 12, 17, 21, 25, 29, 16, 20, 24, 28),
    (7, 0): (7, 6, 5, 4, 3, 2, 1, 0, 15, 14, 13, 12, 11, 10, 9, 8, 23, 22, 21, 20, 19, 18, 17, 16, 31, 30, 29, 28, 27, 26, 25, 24),
    (7, 6): (7, 6, 5, 4, 15, 14, 13, 12, 3, 2, 1, 0, 11, 10, 9, 8, 23, 22, 21, 20, 31, 30, 29, 28, 19, 18, 17, 16, 27, 26, 25, 24),
    (7, 24): (7, 6, 5, 4, 3, 2, 1, 0, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 31, 30, 29, 28, 27, 26, 25, 24),
    (7, 30): (7, 6, 5, 4, 15, 14, 13, 12, 23, 22, 21, 20, 31, 30, 29, 28, 3, 2, 1, 0, 11, 10, 9, 8, 19, 18, 17, 16, 27, 26, 25, 24),
    (7, 60): (7, 6, 15, 14, 23, 22, 31, 30, 5, 4, 13, 12, 21, 20, 29, 28, 3, 2, 11, 10, 19, 18, 27, 26, 1, 0, 9, 8, 17, 16, 25, 24),
    (15, 0): (15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 31, 30, 29, 28, 27, 26, 25, 24, 23, 22, 21, 20, 19, 18, 17, 16),
    (15, 24): (15, 14, 13, 12, 11, 10, 9, 8, 31, 30, 29, 28, 27, 26, 25, 24, 7, 6, 5, 4, 3, 2, 1, 0, 23, 22, 21, 20, 19, 18, 17, 16),
    (31, 0): (31, 30, 29, 28, 27, 26, 25, 24, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0)
}

Subgroups

O_h has 98 individual subgroups, which are all shown in the list below. (A Python dictionary of them can be found here.)

They naturally divide in 33 bundles of similar subgroups, whose elements belong to the same conjugacy classes.
In this article these bundles are given naive names based on some of the colors assigned to their elements (like Dih₄ green orange).
Each of them has a collapsible box below, containing representations of the individual subgroups.

These belong to 25 bigger bundles, which can be identified with a label in Schoenflies or Coxeter notation (like D_2d or [2⁺,4]).
Each of them has a vertex in the big Hasse diagram below.

Four different kinds of Coxeter notation can be distinguished, based on where they contain plus signs:

[...]⁺	rotate
[...]	reflect
[...⁺,...⁺]	cross
[...⁺, ...]	mixed

Hasse diagrams

All 25 bundles of similar subgroups

tetrahedral, rotational and reflective subgroups
(Subgroups of S₄ as an abstract group)	Subgroups of S₄ as the tetrahedral group T_d or [3,3]	Rotational subgroups Subgroups of S₄ as the chiral octahedral group O or [4,3]⁺	Reflective subgroups Coxeter notation is like in the file on the left without the plus signs. But there is no [2,3], and no green edge from [2,2] to [3,3].

chiral tetrahedral and pyritohedral subgroups
Subgroups of A₄ as the chiral tetrahedral group T or [3,3]⁺	Subgroups of A₄×C₂ as the pyritohedral group T_h or [3⁺,4]

List of all subgroups

For the same list including all permutations of the respective example solids, see Full octahedral group/List of all subgroups.

The group itself

O_h S₄ × C₂ [4,3]
		truncated cuboctahedron
		truncated cuboctahedron

Subgroups of order 24

T_d S₄ green orange [3,3]
		nonuniform truncated octahedron
		nonuniform truncated octahedron

O S₄ blue red [4,3]⁺
		nonuniform snub cube
		nonuniform snub cube

T_h A₄ × C₂ [3⁺,4]
		cantic snub octahedron
		cantic snub octahedron

Subgroups of order 16

D_4h Dih₄ × C₂ [2,4]

Subgroups of order 12

T A₄ [3,3]⁺

submatrix

D_3d Dih₆ [2⁺,6]

submatrix

Subgroups of order 8

D_2h C₂³ white [2,2]

D_2h C₂³ green [2,2]

(Below the C₂³ subgroups are shown in more detail.)

C_4h C₄ × C₂ [4⁺,2]

C_4v Dih₄ green red [4]

submatrix

Permutations of the square
for comparison

Cube permutations that
leave the z-axis fixed

D_2d Dih₄ blue orange [2⁺,4]

D_2d Dih₄ green orange [2⁺,4]

	\|	\|	\|

D₄ Dih₄ blue red [2,4]⁺

(Below the Dih₄ subgroups are shown in more detail.)

Subgroups of order 6

C_3v S₃ green [3]

D₃ S₃ blue [2,3]⁺

(Below the S₃ subgroups are shown in more detail.)

S₆ C₆ [2⁺,6⁺]

Subgroups of order 4

S₄ C₄ orange [2⁺,4⁺]

C₄ C₄ red [4]⁺

C_2h = D_1d V inv white [2⁺,2]

C_2h = D_1d V inv green [2⁺,2]

C_2v V green blue yellow [2]

C_2v V yellow white [2]

C_2v V green white [2]

D₂ V blue white [2,2]⁺

D₂ V white [2,2]⁺

Subgroups of order 3

C₃ C₃ [3]⁺

Subgroups of order 2

S₂ C₂ inv [2⁺,2⁺]

C_s = C_1v C₂ yellow [ ]

C_s = C_1v C₂ green [ ]

C₂ C₂ white [2]⁺

C₂ C₂ blue [2]⁺

The trivial group

C₁ C₁ [ ]⁺

Different appearances of the same group

Symmetry group of the cuboid

The symmetry group of the cuboid C₂³ appears in two essentially different ways as a subgroup of O_h.
The one where the cuboid is the cube itself is the most intuitive one.
In the other one the cuboid is the original cube rotated by 45° around an axis. The one where it is rotated around the z-axis is shown below.
There are 4 individual subgroups (see above).

D_2h C₂³ white [2,2]

D_2h C₂³ green [2,2]

Symmetry group of the square

The symmetry group of the square appears in four essentially different ways as a subgroup of O_h. (C_4v or [4] being the most intuitive among them.)
There are 12 individual Dih₄ subgroups (see above). Shown below are the four where the square is seen "from above", i.e. a point on the positive z-axis.

In the white box above the colored boxes of the four subgroups are the permutations of the square. Their 2×2 transformation matrices are the top left submatrices of the four 3×3 matrices in the same column. So the last non-zero entry of the 3×3 matrix determines the permutation in this column. (So each column has only two different permutations.) The pattern of these eight last entries identifies the subgroup. It is shown on the left in the little 4×2 matrix under the example solid.

Square permutations for comparison

C_4v Dih₄ green red [4]

D_2d Dih₄ blue orange [2⁺,4]

D_2d Dih₄ green orange [2⁺,4]

D₄ Dih₄ blue red [2,4]⁺

Symmetry group of the triangle

The symmetry group of the triangle appears in two essentially different ways as a subgroup of O_h, with C_3v or [3] being the most intuitive among them.
There are 8 individual subgroups (see above). Shown below are the ones where the triangle is seen from a point on the negative main diagonal of the coordinate system.

C_3v S₃ green [3]

D₃ S₃ blue [2,3]⁺

Cuboctahedral example solids and contained hexagons

	S₄ blue red	A₄ × C₂	A₄	S₄ green orange
shown above
cuboctahedral
contained hexagon
	S₃ blue	C₆	C₃	S₃ green

Code

The Python code used to create many of the illustrations in this article can be found here: https://github.com/watchduck/full_octahedral_group

The following code shows bijections from pairs to other representations:

S₄ based identifiers

$n'$ is represented as $n+24$ .

(0, 0):  0, (0, 1):  1, (0, 2):  2, (0, 3):  3, (0, 4):  4, (0, 5):  5,
(1, 0): 47, (1, 1): 46, (1, 2): 45, (1, 3): 44, (1, 4): 43, (1, 5): 42,
(2, 0): 40, (2, 1): 41, (2, 2): 37, (2, 3): 36, (2, 4): 39, (2, 5): 38,
(3, 0):  7, (3, 1):  6, (3, 2): 10, (3, 3): 11, (3, 4):  8, (3, 5):  9,
(4, 0): 31, (4, 1): 30, (4, 2): 34, (4, 3): 35, (4, 4): 32, (4, 5): 33,
(5, 0): 16, (5, 1): 17, (5, 2): 13, (5, 3): 12, (5, 4): 15, (5, 5): 14,
(6, 0): 23, (6, 1): 22, (6, 2): 21, (6, 3): 20, (6, 4): 19, (6, 5): 18,
(7, 0): 24, (7, 1): 25, (7, 2): 26, (7, 3): 27, (7, 4): 28, (7, 5): 29

Permutations of cube vertices

The initial order is (-1, -1, -1), (1, -1, -1), (-1, 1, -1), (1, 1, -1), (-1, -1, 1), (1, -1, 1), (-1, 1, 1), (1, 1, 1).

(0, 0): (0, 1, 2, 3, 4, 5, 6, 7), (0, 1): (0, 2, 1, 3, 4, 6, 5, 7), (0, 2): (0, 1, 4, 5, 2, 3, 6, 7), (0, 3): (0, 4, 1, 5, 2, 6, 3, 7), (0, 4): (0, 2, 4, 6, 1, 3, 5, 7), (0, 5): (0, 4, 2, 6, 1, 5, 3, 7),
(1, 0): (1, 0, 3, 2, 5, 4, 7, 6), (1, 1): (1, 3, 0, 2, 5, 7, 4, 6), (1, 2): (1, 0, 5, 4, 3, 2, 7, 6), (1, 3): (1, 5, 0, 4, 3, 7, 2, 6), (1, 4): (1, 3, 5, 7, 0, 2, 4, 6), (1, 5): (1, 5, 3, 7, 0, 4, 2, 6),
(2, 0): (2, 3, 0, 1, 6, 7, 4, 5), (2, 1): (2, 0, 3, 1, 6, 4, 7, 5), (2, 2): (2, 3, 6, 7, 0, 1, 4, 5), (2, 3): (2, 6, 3, 7, 0, 4, 1, 5), (2, 4): (2, 0, 6, 4, 3, 1, 7, 5), (2, 5): (2, 6, 0, 4, 3, 7, 1, 5),
(3, 0): (3, 2, 1, 0, 7, 6, 5, 4), (3, 1): (3, 1, 2, 0, 7, 5, 6, 4), (3, 2): (3, 2, 7, 6, 1, 0, 5, 4), (3, 3): (3, 7, 2, 6, 1, 5, 0, 4), (3, 4): (3, 1, 7, 5, 2, 0, 6, 4), (3, 5): (3, 7, 1, 5, 2, 6, 0, 4),
(4, 0): (4, 5, 6, 7, 0, 1, 2, 3), (4, 1): (4, 6, 5, 7, 0, 2, 1, 3), (4, 2): (4, 5, 0, 1, 6, 7, 2, 3), (4, 3): (4, 0, 5, 1, 6, 2, 7, 3), (4, 4): (4, 6, 0, 2, 5, 7, 1, 3), (4, 5): (4, 0, 6, 2, 5, 1, 7, 3),
(5, 0): (5, 4, 7, 6, 1, 0, 3, 2), (5, 1): (5, 7, 4, 6, 1, 3, 0, 2), (5, 2): (5, 4, 1, 0, 7, 6, 3, 2), (5, 3): (5, 1, 4, 0, 7, 3, 6, 2), (5, 4): (5, 7, 1, 3, 4, 6, 0, 2), (5, 5): (5, 1, 7, 3, 4, 0, 6, 2),
(6, 0): (6, 7, 4, 5, 2, 3, 0, 1), (6, 1): (6, 4, 7, 5, 2, 0, 3, 1), (6, 2): (6, 7, 2, 3, 4, 5, 0, 1), (6, 3): (6, 2, 7, 3, 4, 0, 5, 1), (6, 4): (6, 4, 2, 0, 7, 5, 3, 1), (6, 5): (6, 2, 4, 0, 7, 3, 5, 1),
(7, 0): (7, 6, 5, 4, 3, 2, 1, 0), (7, 1): (7, 5, 6, 4, 3, 1, 2, 0), (7, 2): (7, 6, 3, 2, 5, 4, 1, 0), (7, 3): (7, 3, 6, 2, 5, 1, 4, 0), (7, 4): (7, 5, 3, 1, 6, 4, 2, 0), (7, 5): (7, 3, 5, 1, 6, 2, 4, 0)

Permutations of octahedron vertices

The initial order is (-1, 0, 0), (1, 0, 0), (0, -1, 0), (0, 1, 0), (0, 0, -1), (0, 0, 1).

(0, 0): (0, 1, 2, 3, 4, 5), (0, 1): (2, 3, 0, 1, 4, 5), (0, 2): (0, 1, 4, 5, 2, 3), (0, 3): (4, 5, 0, 1, 2, 3), (0, 4): (2, 3, 4, 5, 0, 1), (0, 5): (4, 5, 2, 3, 0, 1),
(1, 0): (1, 0, 2, 3, 4, 5), (1, 1): (2, 3, 1, 0, 4, 5), (1, 2): (1, 0, 4, 5, 2, 3), (1, 3): (4, 5, 1, 0, 2, 3), (1, 4): (2, 3, 4, 5, 1, 0), (1, 5): (4, 5, 2, 3, 1, 0),
(2, 0): (0, 1, 3, 2, 4, 5), (2, 1): (3, 2, 0, 1, 4, 5), (2, 2): (0, 1, 4, 5, 3, 2), (2, 3): (4, 5, 0, 1, 3, 2), (2, 4): (3, 2, 4, 5, 0, 1), (2, 5): (4, 5, 3, 2, 0, 1),
(3, 0): (1, 0, 3, 2, 4, 5), (3, 1): (3, 2, 1, 0, 4, 5), (3, 2): (1, 0, 4, 5, 3, 2), (3, 3): (4, 5, 1, 0, 3, 2), (3, 4): (3, 2, 4, 5, 1, 0), (3, 5): (4, 5, 3, 2, 1, 0),
(4, 0): (0, 1, 2, 3, 5, 4), (4, 1): (2, 3, 0, 1, 5, 4), (4, 2): (0, 1, 5, 4, 2, 3), (4, 3): (5, 4, 0, 1, 2, 3), (4, 4): (2, 3, 5, 4, 0, 1), (4, 5): (5, 4, 2, 3, 0, 1),
(5, 0): (1, 0, 2, 3, 5, 4), (5, 1): (2, 3, 1, 0, 5, 4), (5, 2): (1, 0, 5, 4, 2, 3), (5, 3): (5, 4, 1, 0, 2, 3), (5, 4): (2, 3, 5, 4, 1, 0), (5, 5): (5, 4, 2, 3, 1, 0),
(6, 0): (0, 1, 3, 2, 5, 4), (6, 1): (3, 2, 0, 1, 5, 4), (6, 2): (0, 1, 5, 4, 3, 2), (6, 3): (5, 4, 0, 1, 3, 2), (6, 4): (3, 2, 5, 4, 0, 1), (6, 5): (5, 4, 3, 2, 0, 1),
(7, 0): (1, 0, 3, 2, 5, 4), (7, 1): (3, 2, 1, 0, 5, 4), (7, 2): (1, 0, 5, 4, 3, 2), (7, 3): (5, 4, 1, 0, 3, 2), (7, 4): (3, 2, 5, 4, 1, 0), (7, 5): (5, 4, 3, 2, 1, 0)

Pairs in reverse colex order

The reverse colexicographic order of permutations is the order of their respective integer values.
The list of permutations of octahedron vertices on the right can be generalized as the infinite list of cross-polytope vertices.
(Its first eight elements are the permutations of the square within a 4×2 matrix.)

cube

octahedron

(0, 0), (0, 2), (0, 1), (0, 4), (0, 3), (0, 5),
(1, 0), (1, 2), (1, 1), (1, 4), (1, 3), (1, 5),
(2, 1), (2, 4), (2, 0), (2, 2), (2, 5), (2, 3),
(3, 1), (3, 4), (3, 0), (3, 2), (3, 5), (3, 3),
(4, 3), (4, 5), (4, 2), (4, 0), (4, 4), (4, 1),
(5, 3), (5, 5), (5, 2), (5, 0), (5, 4), (5, 1),
(6, 5), (6, 3), (6, 4), (6, 1), (6, 2), (6, 0),
(7, 5), (7, 3), (7, 4), (7, 1), (7, 2), (7, 0)

(0, 0), (1, 0), (2, 0), (3, 0), (0, 1), (2, 1), (1, 1), (3, 1),
(4, 0), (5, 0), (6, 0), (7, 0), (4, 1), (6, 1), (5, 1), (7, 1), 
(0, 2), (1, 2), (4, 2), (5, 2), (0, 3), (4, 3), (1, 3), (5, 3), 
(2, 2), (3, 2), (6, 2), (7, 2), (2, 3), (6, 3), (3, 3), (7, 3), 
(0, 4), (2, 4), (4, 4), (6, 4), (0, 5), (4, 5), (2, 5), (6, 5), 
(1, 4), (3, 4), (5, 4), (7, 4), (1, 5), (5, 5), (3, 5), (7, 5)

3×3 matrices

(0, 0): [[ 1, 0, 0], [0, 1, 0], [0, 0, 1]], (0, 1): [[0, 1, 0], [ 1, 0, 0], [0, 0, 1]], (0, 2): [[ 1, 0, 0], [0, 0, 1], [0, 1, 0]], (0, 3): [[0, 1, 0], [0, 0, 1], [ 1, 0, 0]], (0, 4): [[0, 0, 1], [ 1, 0, 0], [0, 1, 0]], (0, 5): [[0, 0, 1], [0, 1, 0], [ 1, 0, 0]],
(1, 0): [[-1, 0, 0], [0, 1, 0], [0, 0, 1]], (1, 1): [[0,-1, 0], [ 1, 0, 0], [0, 0, 1]], (1, 2): [[-1, 0, 0], [0, 0, 1], [0, 1, 0]], (1, 3): [[0,-1, 0], [0, 0, 1], [ 1, 0, 0]], (1, 4): [[0, 0,-1], [ 1, 0, 0], [0, 1, 0]], (1, 5): [[0, 0,-1], [0, 1, 0], [ 1, 0, 0]],
(2, 0): [[ 1, 0, 0], [0,-1, 0], [0, 0, 1]], (2, 1): [[0, 1, 0], [-1, 0, 0], [0, 0, 1]], (2, 2): [[ 1, 0, 0], [0, 0,-1], [0, 1, 0]], (2, 3): [[0, 1, 0], [0, 0,-1], [ 1, 0, 0]], (2, 4): [[0, 0, 1], [-1, 0, 0], [0, 1, 0]], (2, 5): [[0, 0, 1], [0,-1, 0], [ 1, 0, 0]],
(3, 0): [[-1, 0, 0], [0,-1, 0], [0, 0, 1]], (3, 1): [[0,-1, 0], [-1, 0, 0], [0, 0, 1]], (3, 2): [[-1, 0, 0], [0, 0,-1], [0, 1, 0]], (3, 3): [[0,-1, 0], [0, 0,-1], [ 1, 0, 0]], (3, 4): [[0, 0,-1], [-1, 0, 0], [0, 1, 0]], (3, 5): [[0, 0,-1], [0,-1, 0], [ 1, 0, 0]],
(4, 0): [[ 1, 0, 0], [0, 1, 0], [0, 0,-1]], (4, 1): [[0, 1, 0], [ 1, 0, 0], [0, 0,-1]], (4, 2): [[ 1, 0, 0], [0, 0, 1], [0,-1, 0]], (4, 3): [[0, 1, 0], [0, 0, 1], [-1, 0, 0]], (4, 4): [[0, 0, 1], [ 1, 0, 0], [0,-1, 0]], (4, 5): [[0, 0, 1], [0, 1, 0], [-1, 0, 0]],
(5, 0): [[-1, 0, 0], [0, 1, 0], [0, 0,-1]], (5, 1): [[0,-1, 0], [ 1, 0, 0], [0, 0,-1]], (5, 2): [[-1, 0, 0], [0, 0, 1], [0,-1, 0]], (5, 3): [[0,-1, 0], [0, 0, 1], [-1, 0, 0]], (5, 4): [[0, 0,-1], [ 1, 0, 0], [0,-1, 0]], (5, 5): [[0, 0,-1], [0, 1, 0], [-1, 0, 0]],
(6, 0): [[ 1, 0, 0], [0,-1, 0], [0, 0,-1]], (6, 1): [[0, 1, 0], [-1, 0, 0], [0, 0,-1]], (6, 2): [[ 1, 0, 0], [0, 0,-1], [0,-1, 0]], (6, 3): [[0, 1, 0], [0, 0,-1], [-1, 0, 0]], (6, 4): [[0, 0, 1], [-1, 0, 0], [0,-1, 0]], (6, 5): [[0, 0, 1], [0,-1, 0], [-1, 0, 0]],
(7, 0): [[-1, 0, 0], [0,-1, 0], [0, 0,-1]], (7, 1): [[0,-1, 0], [-1, 0, 0], [0, 0,-1]], (7, 2): [[-1, 0, 0], [0, 0,-1], [0,-1, 0]], (7, 3): [[0,-1, 0], [0, 0,-1], [-1, 0, 0]], (7, 4): [[0, 0,-1], [-1, 0, 0], [0,-1, 0]], (7, 5): [[0, 0,-1], [0,-1, 0], [-1, 0, 0]]

Truncated cuboctahedron coordinates

The points of the truncated cuboctahedron are the $2^{3}\cdot 6!=48$ permutations of ${\bigl (}\pm 1,\pm ({\sqrt {2}}+1),\pm (2{\sqrt {2}}+1){\bigr )}$ .
E.g. $(5,4)=(1,-b,a)=(1,-2{\sqrt {2}}-1,{\sqrt {2}}+1)$ .

a = sqrt(2) + 1
b = 2*sqrt(2) + 1

(0, 0): (-b, -a, -1), (0, 1): (-a, -b, -1), (0, 2): (-b, -1, -a), (0, 3): (-a, -1, -b), (0, 4): (-1, -b, -a), (0, 5): (-1, -a, -b),
(1, 0): ( b, -a, -1), (1, 1): ( a, -b, -1), (1, 2): ( b, -1, -a), (1, 3): ( a, -1, -b), (1, 4): ( 1, -b, -a), (1, 5): ( 1, -a, -b),
(2, 0): (-b,  a, -1), (2, 1): (-a,  b, -1), (2, 2): (-b,  1, -a), (2, 3): (-a,  1, -b), (2, 4): (-1,  b, -a), (2, 5): (-1,  a, -b),
(3, 0): ( b,  a, -1), (3, 1): ( a,  b, -1), (3, 2): ( b,  1, -a), (3, 3): ( a,  1, -b), (3, 4): ( 1,  b, -a), (3, 5): ( 1,  a, -b),
(4, 0): (-b, -a,  1), (4, 1): (-a, -b,  1), (4, 2): (-b, -1,  a), (4, 3): (-a, -1,  b), (4, 4): (-1, -b,  a), (4, 5): (-1, -a,  b),
(5, 0): ( b, -a,  1), (5, 1): ( a, -b,  1), (5, 2): ( b, -1,  a), (5, 3): ( a, -1,  b), (5, 4): ( 1, -b,  a), (5, 5): ( 1, -a,  b),
(6, 0): (-b,  a,  1), (6, 1): (-a,  b,  1), (6, 2): (-b,  1,  a), (6, 3): (-a,  1,  b), (6, 4): (-1,  b,  a), (6, 5): (-1,  a,  b),
(7, 0): ( b,  a,  1), (7, 1): ( a,  b,  1), (7, 2): ( b,  1,  a), (7, 3): ( a,  1,  b), (7, 4): ( 1,  b,  a), (7, 5): ( 1,  a,  b)

These are Python dictionaries without the surrounding braces. (Dicts work only in one direction, but bidict can be used to get back to the pairs.)

A dictionary of these permutations and their properties (including conjugacy class and inverse) can be found here.

A dictionary of all the subgroups can be found here (as a bijection from naive names to tuples of S₄ based numbers).

Cayley table

S4

pairs

Overview

Truncated cuboctahedron

8×6 matrix

Hexagon corresponding to top matrix row

Cubes corresponding to matrix columns

Conjugacy classes

Subgroups

Hasse diagrams

List of all subgroups

The group itself

Subgroups of order 24

Subgroups of order 16

Subgroups of order 12

Subgroups of order 8

Subgroups of order 6

Subgroups of order 4

Subgroups of order 3

Subgroups of order 2

The trivial group

Different appearances of the same group

Symmetry group of the cuboid

Symmetry group of the square

Symmetry group of the triangle

Cuboctahedral example solids and contained hexagons

Code

S₄