Symmetric group S4

Cycle graph of S₄

The symmetric group S₄ is the group of all permutations of 4 elements.

It has 4!=24 elements and is not abelian.

Even permutations are white:

• the identity
• eight 3-cycles
• three double-transpositions

Odd permutations are colored:

• six transpositions (green)
• six 4-cycles (orange)

The small table on the left shows the permuted elements, and inversion vectors (which are reflected factorial numbers) below them.
Another column shows the inversion sets, ordered like .
(When a dot with the numbers i,j is marked red, than the elements on places i,j are out of their natural order.)

The digit sums of the inversion vectors (or factorial numbers) and the cardinalities of the inversion sets are equal.
They form the sequence  A034968. A permutation and its corresponding digit sum have the same parity.

The big table on the right is the Cayley table of S₄.
It could also be given as the matrix multiplication table of the shown permutation matrices. (Compare multiplication table for S₃)

Permutations of 4 elements

Cayley table of S4 See also: A closer look at the Cayley table

Subgroups

There are 30 subgroups of S₄, including the group itself and the 10 small subgroups.

Every group has as many small subgroups as neutral elements on the main diagonal:
The trivial group and two-element groups Z₂. These small subgroups are not counted in the following list.

Order 12

The alternating group A₄ showing only the even permutations

Subgroups:

Cycle graphs
Alternating group A4 Subgroups:

Order 8

Dihedral group of order 8 Subgroups:

Dihedral group of order 8 Subgroups:

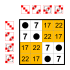Dihedral group of order 8 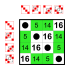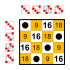Subgroups: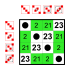

Cycle graphs
Dihedral group of order 8 Subgroups:   Dihedral group of order 8 Subgroups:   Dihedral group of order 8 Subgroups:

Order 6

Symmetric group S3 Subgroup:

Symmetric group S3 Subgroup:

Symmetric group S3 Subgroup:

Symmetric group S3 Subgroup:

Cycle graphs
Symmetric group S3 Subgroup: Symmetric group S3 Subgroup: Symmetric group S3 Subgroup: Symmetric group S3 Subgroup:

Order 4

Klein four-group	Klein four-group	Klein four-group	Klein four-group
Cyclic group Z4	Cyclic group Z4	Cyclic group Z4

Cycle graphs
Klein four-group Klein four-group Klein four-group Klein four-group Cyclic group Z4 Cyclic group Z4 Cyclic group Z4

Order 3

Cyclic group Z3

Cyclic group Z3

Cyclic group Z3

Cyclic group Z3

Cycle graphs
Cyclic group Z3 Cyclic group Z3 Cyclic group Z3 Cyclic group Z3

Lattice of subgroups

The subgroups of every group form a lattice:

Index for the Hasse diagram on the right Subgroups are represented by their cycle graphs.

Lattice of subgroups Hasse diagram Different colors are just for better readability.

Weak order of permutations

The permutations of n elements form a lattice.
A permutation may be defined by its set of inversions;
and the lattice by the subset relation $\subseteq$ between these sets.
Or a permutation my be defined by its factorial number (or inversion vector);
and the lattice by the bitwise less than or equal relation $\le$ between them.

Permutohedron

The Hasse diagram of the weak order of permutations is the permutohedron. For the symmetric group S₄ it's the truncated octahedron.

Permutohedron of S4	Permutations represented by their sets of inversions
Schlegel diagram of the truncated octahedron	In the Schlegel diagram, the inversions show a remarkable symmetry.
Permutations represented by matrices	Permutations represented by permuted elements, and inversion vectors below them (compare convex version)

The edges of the permutohedron match transpositions, i.e. permutations exchanging only two elements.

When two permutations are linked by a highlighted edge, representing one of six transpositions,
this transposition turns one permutation into the other and vice versa.

E.g. in the top permutohedron the permutations 3 and 5 are linked by a highlighted edge, representing transposition 2.
So 2∘3=5 and 2∘5=3.            The Function composition g∘f   (spoken "g of f" or "g after f")   tells, that first f is done, and then g.

This file shows the same bits like the files and above, but with a single permutohedron for each inversion.
The highlighted edges from the file above are also shown.
A vertex is red , when it's higher than such an edge - i.e. when an arrow points in its direction directly or indirectly.
The red vertices always form a compound of two hexagons and two squares.

Join and meet

If one wants to have join and meet of any two permutations, one can find them in the permutohedron. The following table shows all relevant pairs of permutations. The arguments (row and column of the table) and their join and meet are shown by red vertices in the little permutohedra. The highest red vertex is always the join $\cup$ and the lowest red vertex is the meet $\cap$.

Join and meet in permutohedra

The following join table is derived from the table above. Besides the decimal enumeration, it shows also the inversion sets and factorial numbers. (The meet table is like this one, but reflected about the subdiagonal, and with all numbers replaced by their difference with 23.)

Join table of the weak order of permutations

Positions of the entries in the join table

It's worth taking a look at the number of red squares in the 24 matrices above:

Number of entries in join and meet table
This permutohedron shows, how often an element appears in the join table - i.e. how many red squares are in the 24 matrices above. And these are the numbers for the meet table.

The table becomes more interesting, looking only at the inversion bits. This file shows the bits of every inversion in a single matrix:

This file shows the same bits like the join table above, but with a single matrix for each inversion.

One can see, that for the three inversions comparing consecutive places, the join operation is simply the union of the inversion sets. For the two inversions comparing places with one place between, there are 32 darker red fields beyond the union. For the inversion comparing the first and the last place, there are 56 darker fields beyond the union. So the union of two permutations inversion sets is always a subset to the inversion set of the permutations' join.

A closer look at the Cayley table

The Cayley table again

Every entry appears exactly one time in every row and column of the Cayley table.
So the positions of the entries form 24 permutation matrices:

Positions of the entries in the Cayley table

Rows and columns of the Cayley table match permutations of 24 elements.
Below they are also represented as permutation matrices:

Rows as permutations

Columns as permutations

Generators and Cayley graphs

Rhombicuboctahedron - Generators 4, 9 or (132), (1234)

Truncated cube - Generators 1, 8 or (12), (234)

Truncated octahedron

Generators 1, 9 or (12), (1234)

Generators 1, 2, 6 or (12), (23), (34)

(compare convex version)

Cayley graph and permutohedron
This graph is related to the permutohedron: Self inverse permutations (symmetric matrices) are on the same positions, all other permutations are replaced by their inverses (transposed matrices). Permutohedron for comparison

Nauru graph - Generators 1, 5, 21 or (12), (13), (14)

Torus embedding

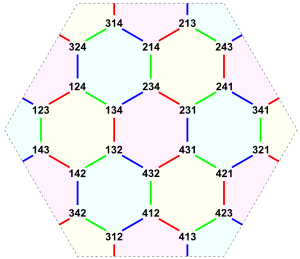Sequences with the first digit omitted Triples linked by an edge differ in only one digit. The edge color tells by which: 1st, 2nd, 3rd

Generalized Petersen graph

Adjacency matrix

Adjacency matrix of the Nauru graph

Bit permutations

When the permutations p_n of 4 elements are applied on the reverse binary digits of the integers 0...15,
they generate permutations P_n of 16 elements, which also form the symmetric group S₄.
Walsh permutation; bit permutation

    Cycle graphs of S₄ with permutations p_n and P_n

Gray code order (Steinhaus–Johnson–Trotter algorithm)

The algorithm defines a Hamiltonian path in a Cayley graph of the symmetric group. The inverse permutations define a path in the permutohedron:
Cayley graph	Permutohedron
Permutations form a Gray code. The swapped elements are always adjacent.	Permutations, inversion vectors and inversion sets form a Gray code.
Permutations with green or orange background are odd. The smaller numbers below the permutations are the inversion vectors. Red marks indicate swapped elements.