Wright State University Lake Campus/2019-1/Phy2400/Final formula sheet

00-Mathematics for this course

$\theta =s/r$

${\vec {A}}+{\vec {B}}={\vec {C}}$ ${\vec {B}}={\vec {C}}-{\vec {A}}$

Circle's circumference (area): $C_{\odot }=\,2\pi r\,(A_{\odot }=\,\pi r^{2})$.

Sphere's area (volume): $A_{\bigcirc }=4\pi r^{2}\,(V_{\bigcirc }={\frac {4}{3}}\pi r^{3})$

Unit vectors: ${\vec {A}}=A_{x}\,{\hat {i}}+A_{y}\,{\hat {j}}$. Other notations: $({\hat {x}},{\hat {y}})$, and $({\widehat {e_{1}}},{\widehat {e_{2}}})$

${\vec {r}}=x{\hat {x}}+y{\hat {y}}$. Magnitude: $A\equiv |{\vec {A}}|={\sqrt {A_{x}^{2}+A_{y}^{2}}}\quad$.

In first quadrant: $\tan \theta =y/x$ leads to $\theta =\arctan {(y/x)}\quad$

${\vec {A}}+{\vec {B}}={\vec {C}}\Leftrightarrow$ $A_{x}+B_{x}=C_{x}$ and $A_{y}+B_{y}=C_{y}$

01-Introduction

Text Symbol Factor Exponent giga G 1000000000 E9 mega M 1000000 E6 kilo k 1000 E3 (none) (none) 1 E0 centi c 0.01 E−2 milli m 0.001 E−3 micro μ 0.000001 E−6 nano n 0.000000001 E−9 pico p 0.000000000001 E−12

• 1 kilometer = .621 miles and 1 MPH = 1 mi/hr ≈ .447 m/s
• Typically air density is 1.2kg/m³, with pressure 10⁵Pa. The density of water is 1000kg/m³.
• Earth's mean radius ≈ 6371km, mass ≈ 6×10²⁴
   kg, and gravitational acceleration = g ≈ 9.8m/s²
• Universal gravitational constant = G ≈ 6.67×10⁻¹¹
   m³·kg⁻¹·s⁻²
• 1 amu = 1 u ≈ 1.66 × 10^-27 kg is the approximate mass of a proton or neutron.
• Boltzmann's constant = k_B≈ 1.38 × 10^-23 J K⁻¹ , and the gas constant is R = N_Ak_B≈8.314 J  K⁻¹  mol⁻¹, where N_A≈ 6.02 × 10²³ is the Avogadro number.

02-One dimensional kinematics

Difference: $\delta {\mathcal {X}}$: $\Delta {\mathcal {X}}={\mathcal {X}}_{f}-{\mathcal {X}}_{i}$ Average (mean): ${\bar {\mathcal {X}}}=\langle {\mathcal {X}}\rangle ={\mathcal {X}}_{\text{ave}}=\Sigma {\mathcal {X}}_{i}{\mathcal {/}}N\ {\text{or}}\ \Sigma {\mathcal {P}}_{i}{\mathcal {X}}_{i}$. Average velocity: ${\bar {v}}=\Delta x/\Delta t$

03-Two-Dimensional Kinematics

$x=x_{0}+v_{0x}\Delta t+{\frac {1}{2}}a_{x}\Delta t^{2}$	$v_{x}=v_{0x}+a_{x}\Delta t$	$v_{x}^{2}=v_{x0}^{2}+2a_{x}\Delta x$
$y=y_{0}+v_{0y}\Delta t+{\frac {1}{2}}a_{y}\Delta t^{2}$	$v_{y}=v_{0y}+a_{y}\Delta t$	$v_{y}^{2}=v_{x0}^{2}+2a_{y}\Delta y$

$v^{2}=v_{0}^{2}+2a_{x}\Delta x+2a_{y}\Delta y$   ...in advanced notation this becomes $\Delta (v^{2})=2{\vec {a}}\cdot \Delta {\vec {\ell }}$.

In free fall we often set, a_x=0 and a_y= -g. If angle is measured with respect to the x axis:

$v_{x}=v\cos \theta$       $v_{y}=v\sin \theta$       $v_{x0}=v_{0}\cos \theta _{0}$       $v_{y0}=v_{0}\sin \theta _{0}$

04-Dynamics: Force and Newton's Laws

$m{\vec {a}}=\sum {\vec {F}}_{j}\,$ and ${\vec {F}}_{ij}=-{\vec {F}}_{ji}$.

For important forces: Normal $(N\,or\,n)$ is perpendicular to surface; Friction $(f)$ is parallel to surface; Tension $(T)$ is along a rope or string; Weight $(w=mg)$ where $g\approx 9.8m/s^{2}$ at Earth's surface.

     The x and y components of the three forces of tension on the small grey circle where the three "massless" ropes meet are:

$T_{1x}=-T_{1}\cos \theta _{1}$ ,        $T_{1y}=T_{1}\sin \theta _{1}$

$T_{2x}=0$ ,                             $T_{2y}=-mg$

$T_{3x}=T_{3}\cos \theta _{3}$ ,          $T_{3y}=T_{3}\sin \theta _{3}$

05-Friction, Drag, and Elasticity

• $f_{k}=\mu _{k}N$ is an approximation for the force friction when an object is sliding on a surface, where μ_k ("mew-sub-k") is the kinetic coefficient of friction, and N is the normal force.
• $f_{s}\leq \mu _{s}N$ approximates the maximum possible static friction that canoccurs before the object begins to slide.
• Air drag: $D$ depends on velocity, size, and shape.

06-Uniform Circular Motion and Gravitation

uniform circular motion (here the Latin d was used instead of the Greek Δ

• $2\pi \;rad=360\;deg=1\;rev$ relates the radian, degree, and revolution.

• $f={\frac {\#\,{\text{revs}}}{\#\,{\text{secs}}}}$ is the number of revolutions per second, called frequency.

• $T={\frac {\#\,{\text{secs}}}{\#\,{\text{revs}}}}$ is the number of seconds per revolution, called period. Obviously $fT=1$.

• $\omega ={\frac {\Delta \theta }{\Delta t}}$ is called angular frequency (ω is called omega, and θ is measured in radians). Obviously $\omega T=2\pi$

• $a={\frac {v^{2}}{r}}=\omega v=\omega ^{2}r$ is the acceleration of uniform circular motion, where v is speed, and r is radius.
• $v=\omega r=2\pi r/T$, where T is period.

• $F=G{\frac {mM}{r^{2}}}=mg^{*}$ is the force of gravity between two objects, where the universal constant of gravity is G ≈ 6.674 × 10^-11 m³·kg⁻¹·s⁻².

07-Work and Energy

• $KE={\frac {1}{2}}mv^{2}\,$ is kinetic energy, where m is mass and v is speed..
• $U_{g}=mgy$ is gravitational potential energy,where y is height, and $g=9.80\;{\frac {m}{s^{2}}}$ is the gravitational acceleration at Earth's surface.
• $U_{s}={\frac {1}{2}}k_{s}x^{2}$ is the potential energy stored in a spring with spring constant $k_{s}$.
• $\sum KE_{f}+\sum PE_{f}=\sum KE_{i}+\sum PE_{i}-Q$ relates the final energy to the initial energy. If energy is lost to heat or other nonconservative force, then Q>0.
• $W=F\ell \cos \theta ={\vec {F}}\cdot {\vec {\ell }}$ (measured in Joules) is the work done by a force $F$ as it moves an object a distance $\ell$. The angle between the force and the displacement is θ.
• $\sum {\vec {F}}\cdot \Delta \ell$ describes the work if the force is not uniform. The steps, $\Delta {\vec {\ell }}$, taken by the particle are assumed small enough that the force is approximately uniform over the small step. If force and displacement are parallel, then the work becomes the area under a curve of F(x) versus x.
• $P={\frac {{\vec {F}}\cdot {\vec {\Delta }}\ell }{\Delta t}}={\vec {F}}\cdot {\vec {v}}$ is the power (measured in Watts) is the rate at which work is done. (v is velocity.)

08-Linear Momentum and Collisions

• ${\vec {p}}=m{\vec {v}}$ is momentum, where m is mass and ${\vec {v}}$ is velocity. The net momemtum is conserved if all forces between a system of particles are internal (i.e., come equal and opposite pairs):
• $\sum {\vec {p}}_{f}=\sum {\vec {p}}_{i}$.
• ${\bar {F}}\Delta t=\Delta p$ is the impulse, or change in momentum associated with a brief force acting over a time interval $\Delta t$. (Strictly speaking, ${\bar {F}}$ is a time-averaged force defined by integrating over the time interval.)

09-Statics and Torque

• $\tau =rF\sin \theta ,\!$ is the torque caused by a force, F, exerted at a distance ,r, from the axis. The angle between r and F is θ.

The SI units for torque is the newton metre (N·m). It would be inadvisable to call this a Joule, even though a Joule is also a (N·m). The symbol for torque is typically τ, the Greek letter tau. When it is called moment, it is commonly denoted M. The lever arm is defined as either r, or r_⊥. Labeling r as the lever arm allows moment arm to be reserved for r_⊥.

10-Rotational Motion and Angular Momentum

Linear motion	Angular motion
$x-x_{0}=v_{0}t+{\frac {1}{2}}at^{2}$	$\theta -\theta _{0}=\omega _{0}t+{\frac {1}{2}}\alpha t^{2}$
$v=v_{0}+at\,$	$\omega =\omega _{0}+\alpha t\,$
$x-x_{0}={\frac {1}{2}}(v_{0}+v)t$	$\theta -\theta _{0}={\frac {1}{2}}(\omega _{0}+\omega )t$
$v^{2}=v_{0}^{2}+2a(x-x_{0})\,$	$\omega ^{2}=\omega _{0}^{2}+2\alpha (\theta -\theta _{0})$

The following table refers to rotation of a rigid body about a fixed axis: $\mathbf {s}$ is arclength, $\mathbf {r}$ is the distance from the axis to any point, and $\mathbf {a} _{\mathbf {t} }$ is the tangential acceleration, which is the component of the acceleration that is parallel to the motion. In contrast, the centripetal acceleration, $\mathbf {a} _{\mathbf {c} }=v^{2}/r=\omega ^{2}r$, is perpendicular to the motion. The component of the force parallel to the motion, or equivalently, perpendicular, to the line connecting the point of application to the axis is $\mathbf {F} _{\perp }$. The sum is over $\mathbf {j} \ =1\ \mathbf {to} \ N$ particles or points of application.

Analogy between Linear Motion and Rotational motion

Linear motion	Rotational motion	Defining equation
Displacement = $\mathbf {x}$	Angular displacement = $\theta$	$\theta =\mathbf {x} /\mathbf {r}$
Velocity = $\mathbf {v}$	Angular velocity = $\omega$	$\omega =\mathbf {d} \theta /\mathbf {dt} =\mathbf {v} /\mathbf {r}$
Acceleration = $\mathbf {a}$	Angular acceleration = $\alpha$	$\alpha =\mathbf {d} \omega /\mathbf {dt} =\mathbf {a_{\mathbf {t} }} /\mathbf {r}$
Mass = $\mathbf {m}$	Moment of Inertia = $\mathbf {I}$	$\mathbf {I} =\sum \mathbf {m_{j}} \mathbf {r_{j}} ^{2}$
Force = $\mathbf {F} =\mathbf {m} \mathbf {a}$	Torque = $\tau =\mathbf {I} \alpha$	$\tau =\sum \mathbf {r_{j}} \mathbf {F} _{\perp }\mathbf {_{j}} =\sum \mathbf {r_{\perp j}} \mathbf {F} _{\mathbf {_{j}} }$
Momentum= $\mathbf {p} =\mathbf {m} \mathbf {v}$	Angular momentum= $\mathbf {L} =\mathbf {I} \omega$	$\mathbf {L} =\sum \mathbf {r_{j}} \mathbf {p} \mathbf {_{j}}$
Kinetic energy = ${\frac {1}{2}}\mathbf {m} \mathbf {v} ^{2}$	Kinetic energy = ${\frac {1}{2}}\mathbf {I} \omega ^{2}$	${\frac {1}{2}}\sum \mathbf {m_{j}} \mathbf {v_{j}} ^{2}={\frac {1}{2}}\sum \mathbf {m_{j}} \mathbf {r_{j}} ^{2}\omega ^{2}$

11-Fluid statics

Pressure is the weight per unit area of the fluid above a point.

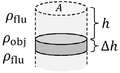
Pressure versus Depth: A fluid's pressure is F/A where F is force and A is a (flat) area. The pressure at depth, $h$ below the surface is the weight (per area) of the fluid above that point. As shown in the figure, this implies:

$P=P_{0}+\rho gh$

where $P_{0}$ is the pressure at the top surface, $h$ is the depth, and $\rho$ is the mass density of the fluid. In many cases, only the difference between two pressures appears in the final answer to a question, and in such cases it is permissible to set the pressure at the top surface of the fluid equal to zero. In many applications, it is possible to artificially set $P_{0}$ equal to zero, for example at atmospheric pressure. The resulting pressure is called the gauge pressure, for $P_{gauge}=\rho gh$ below the surface of a body of water.

Buoyancy and Archimedes' principle Pascal's principle does not hold if two fluids are separated by a seal that prohibits fluid flow (as in the case of the piston of an internal combustion engine). Suppose the upper and lower fluids shown in the figure are not sealed, so that a fluid of mass density $\rho _{flu}$ comes to equilibrium above and below an object. Let the object have a mass density of $\rho _{obj}$ and a volume of $A\Delta h$, as shown in the figure. The net (bottom minus top) force on the object due to the fluid is called the buoyant force:

${\rm {{buoyant}\;{\rm {{force}=(A\Delta h)(\rho _{flu})g\,}}}}$,

and is directed upward. The volume in this formula, AΔh, is called the volume of the displaced fluid, since placing the volume into a fluid at that location requires the removal of that amount of fluid. Archimedes principle states:

A body wholly or partially submerged in a fluid is buoyed up by a force equal to the weight of the displaced fluid.

Note that if $\rho _{obj}=\rho _{flu}$, the buoyant force exactly cancels the force of gravity. A fluid element within a stationary fluid will remain stationary. But if the two densities are not equal, a third force (in addition to weight and the buoyant force) is required to hold the object at that depth. If an object is floating or partially submerged, the volume of the displaced fluid equals the volume of that portion of the object which is below the waterline.

12-Fluid dynamics

A fluid element speeds up if the area is constricted.

• ${\frac {\Delta V}{\Delta t}}={\dot {V}}=Av=Q$ the volume flow for incompressible fluid flow if viscosity and turbulence are both neglected. The average velocity is $v$ and $A$ is the cross sectional area of the pipe. As shown in the figure, $v_{1}A_{1}=v_{2}A_{2}$ because $Av$ is constant along the developed flow. To see this, note that the volume of pipe is $\Delta V=A\Delta x$ along a distance $\Delta x$. And, $v=\Delta x/\Delta t$ is the volume of fluid that passes a given point in the pipe during a time $\Delta t$.
• $P_{1}+\rho gy_{1}+{\frac {1}{2}}\rho v_{1}^{2}=P_{2}+\rho gy_{2}+{\frac {1}{2}}\rho v_{2}^{2}$ is Bernoulli's equation, where $P$ is pressure, $\rho$ is density, and $y$ is height. This holds for inviscid flow.

13-Temperature, Kinetic Theory, and Gas Laws

• $T_{C}=T_{K}-273.15$ converts from Celsius to Kelvins, and $T_{F}={\frac {9}{5}}T_{C}+32$ converts from Celsius to Fahrenheit.
• $PV=nRT=Nk_{B}T$ is the ideal gas law, where P is pressure, V is volume, n is the number of moles and N is the number of atoms or molecules. Temperature must be measured on an absolute scale (e.g. Kelvins).
• N_Ak_B=R where N_A= 6.02 × 10²³ is the Avogadro number. Boltzmann's constant can also be written in eV and Kelvins: k_B ≈8.6 × 10^-5 eV/deg.
• ${\frac {3}{2}}k_{B}T={\frac {1}{2}}mv_{rms}^{2}$ is the average translational kinetic energy per "atom" of a 3-dimensional ideal gas.
• $v_{rms}={\sqrt {\frac {3k_{B}T}{m}}}={\sqrt {\overline {v^{2}}}}$ is the root-mean-square speed of atoms in an ideal gas.
• $E={\frac {\varpi }{2}}Nk_{B}T$ is the total energy of an ideal gas, where $\varpi =3\;$

15-Thermodynamics

• Pressure (P), Energy (E), Volume (V), and Temperature (T) are state variables (state functionscalled state functions). The number of particles (N) can also be viewed as a state variable.
• Work (W), Heat (Q) are not state variables.

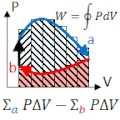
A point on a PV diagram define's the system's pressure (P) and volume (V). Energy (E) and pressure (P) can be deduced from equations of state: E=E(V,P) and T=T(V,P). If the piston moves, or if heat is added or taken from the substance, energy (in the form of work and/or heat) is added or subtracted. If the path returns to its original point on the PV-diagram (e.g., 12341 along the rectantular path shown), and if the process is quasistatic, all state variables (P, V, E, T) return to their original values, and the final system is indistinguishable from its original state.

The net work done per cycle is area enclosed by the loop. This work equals the net heat flow into the system, $Q_{in}-Q_{out}$ (valid only for closed loops).

Remember: Area "under" is the work associated with a path; Area "inside" is the total work per cycle.

• $\Delta W=-P\Delta V$ is the work done on a system of pressure P by a piston of voulume V. If ΔV>0 the substance is expanding as it exerts an outward force, so that ΔW<0 and the substance is doing work on the universe; ΔW>0 whenever the universe is doing work on the system.
• $\Delta Q$ is the amount of heat (energy) that flows into a system. It is positive if the system is placed in a heat bath of higher temperature. If this process is reversible, then the heat bath is at an infinitesimally higher temperature and a finite ΔQ takes an infinite amount of time.
• $\Delta E=\Delta Q-P\Delta V$ is the change in energy (First Law of Thermodynamics).

16-Oscillatory Motion and Waves

• CALCULUS: $(d/dx)\sin kx=k\cos kx,\quad (d/dx)\cos kx=-k\sin kx$

• $x=x_{0}\cos {\frac {2\pi t}{T}}=x_{0}\cos {\omega t}$ where T is period..
• $x(t)=x_{0}\cos \left(\omega _{0}t-\varphi \right)$. For example, $\cos \left(\omega _{0}t-\varphi \right)=\sin \omega _{0}t$.

• $\omega _{0}={\sqrt {\frac {k_{s}}{m}}}$ (m=mass, k_s=spring constant.)$\omega _{0}={\sqrt {\frac {g}{L}}}$ (L=lenghth of low-amplitude simple pendulum.)

• $PE={\frac {1}{2}}k_{s}x^{2}$ is the potential energy of a mass spring system.

Let $x(t)=x_{0}\cos \left(\omega _{0}t-\varphi \right)=$ describe position:

• $v(t)=dx/dt=-\omega _{0}x_{0}\sin \left(\omega _{0}t-\varphi \right)=v_{0}\cos \left(\omega _{0}t+...\right)$, where $v_{0}=\omega _{0}x_{0}$ is maximum velocity.
• $a(t)=dv/dt=-\omega _{0}v_{0}\cos \left(\omega _{0}t-\varphi \right)=a_{0}\cos \left(\omega _{0}t+...\right)$, where $a_{0}=\omega _{0}v_{0}=\omega _{0}^{2}x_{0}$, is maximum acceleration.
• $F_{0}=ma_{0}$, relates maximum force to maximum acceleration.
• $E={\frac {1}{2}}mv_{0}^{2}={\frac {1}{2}}k_{s}x_{0}^{2}$ is the total energy.
• CALCULUS: x(t) obeys the linear homogeneous differential equation (ODE), ${\frac {d^{2}x}{dt^{2}}}=-\omega _{0}^{2}x(t)$

• $f\lambda =v_{p}$ relates the frequency, f, wavelength, λ,and the the phase speed, v_p of the wave (also written as v_w) This phase speed is the speed of individual crests, which for sound and light waves also equals the speed at which a wave packet travels.
• $L={\frac {n\lambda _{n}}{2}}$ describes the n-th normal mode vibrating wave on a string that is fixed at both ends (i.e. has a node at both ends). The mode number, n = 1, 2, 3,..., as shown in the figure.

17-Physics of Hearing

• $v_{s}={\sqrt {\frac {T}{273}}}\cdot 331{\text{m/s}}$ is the the approximate speed near Earth's surface, where the temperature, T, is measured in Kelvins.
• $v_{s}={\sqrt {\frac {F}{\mu }}}$ is the speed of a wave in a stretched string if $F$ is the tension and $\mu$ is the linear mass density (kilograms per meter).