University of Florida/Eml4507/s13 Report 4 Team 7
Problem 1
[edit | edit source]On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.
Find
[edit | edit source]Find the eigenvector x2 corresponding to the eigenvalue λ2 for the spring-mass-damper system on p. 53-13. Plot and comment on this mode shape. Verify that the eigenvectors are orthogonal to each other.
Given
[edit | edit source]The spring-mass-damper system shown on p. 53-13.
Solution
[edit | edit source]I=identity matrix
Need to find an eigenvector where
![]()
By solving this matrix, and setting x1=1, then two equations are created.
k1+k2-γ2-k2x2=0
and
-k2+(k2+k3-γ2)x2=0
Therefore,
x2=(γ2-k1)/(k3-γ2)
Two eigenvectors are orthogonal if their dot product is 0.
The dot product of x1 and x2 however is not 0, therefore they are not orthogonal.
Problem 2
[edit | edit source]On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.
Find
[edit | edit source]Find, plot and compare the eigenvectors.
Compare the mode shapes using two different assumptions.
Animate each format in the given sine wave.
Given
[edit | edit source]|
|
(2.1) |
Solve for the eigenvectors under two differing assumptions:
|
and |
(2.2) |
Mode shapes were plotted according to
where is the circular frequency,
is the eigenvalue . is the eigenvalue .
Solution
[edit | edit source]Firstly, the eigenvectors must be found. The assumption is in effect. These values were found with
|
|
(2.3) |
|
|
(2.4) |
|
|
(2.5) |
and now, The assumption is in effect.
|
|
(2.6) |
|
|
(2.7) |
|
|
(2.8) |
and now, The assumption is in effect. These values were found with
|
|
(2.9) |
|
|
(2.10) |
|
|
(2.11) |
and now, The assumption is in effect.
|
|
(2.12) |
|
|
(2.13) |
|
|
(2.14) |
Now with these values solved for, construct the eigenvectors:
|
and
M1 =[
1.618 -.618;
1 1;
];
quiver(0,0,M1(1,1),M1(2,1));
hold on;
quiver(0,0,M1(1,2),M1(2,2));
M2 =[
1 1;
0.618 -1.618;
];
quiver(0,0,M2(1,1),M2(2,1));
hold on;
quiver(0,0,M2(1,2),M2(2,2));
%% Sine wave:
x1lambda1 = [1.618;
1;];
x2lambda1 = [-.618;
1;];
x1lambda2 = [1;
.618;];
x2lambda2 = [1;
-1.618;];
omega1 = sqrt(4 - sqrt(5));
omega2 = sqrt(4 + sqrt(5));
t = 0:pi/30:4*pi;
x1 = x1lambda1*sin(omega1*t);
x2 = x2lambda1*sin(omega1*t);
x3 = x1lambda2*sin(omega2*t);
x4 = x2lambda2*sin(omega2*t);
figure;
%mode 1
plot(t,x1);
plot(t,x2);
%mode 2
plot(t,x3);
plot(t,x4);
|


Mode 1 and Mode 2 have the same angle between vectors. Mode 2 is flipped over the line.
Modes animated according to sine graphs:


Problem 3
[edit | edit source]On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.
Find
[edit | edit source]Discuss the computational efficiency of Method 1 (root sum squared method) vs. Method 2 (transformation matrix method)
Solution
[edit | edit source]The root sum square method is less useful than the transformation matrix method because the Transformation Matrix method can be used for all other elements where as the root sum square method can be used only for the bar elements as stated in MTG 23.
The overall forces in Method 1 are found by summing the squares of each component (x,y,z) and then taking the square root of that sum for the overall force and direction of the 2D or 3D system.
Both methods use the relation that F=kd but method two goes through more steps to allow a better way for finding the stresses in each element together instead of individually.
In the end both methods will give the same answer but Method 2 is more useful when more elements are involved.
Problem 4
[edit | edit source]On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.
Find
[edit | edit source]The Lowest 3 eigenpairs and plot the 3 lowest mode shapes in a gif image.
Given
[edit | edit source]
Solution
[edit | edit source]
%GIVENS
L=0.3;
E=100e9;
A=1e-4;
rho=5000;
ep=[E A];
%ELEMENT DOF
Edof=zeros(25,5);
for i=1:6
j=2*(i-1);
Edof(i,:)=[i,1+j,2+j,3+j,4+j];
end
for i=7:12
j=2*(i+1);
Edof(i,:)=[i,j-1,j,j+1,j+2];
end
for i=13:19
j=2*(i-13);
Edof(i,:)=[i,1+j,2+j,15+j,16+j];
end
for i=20:25
j=2*(i-20);
Edof(i,:)=[i,1+j,2+j,17+j,18+j];
end
%COORDINATES
ex=zeros(14,2);
ey=zeros(14,2);
for i=1:25
if i<7
ex(i,:)=[L*(i-1),L*i];
ey(i,:)=[0,0];
elseif i>6&&i<13
ex(i,:)=[L*(i-7),L*(i-6)];
ey(i,:)=[L,L];
elseif i>12&&i<20
ex(i,:)=[L*(i-13),L*(i-13)];
ey(i,:)=[0,L];
else
ex(i,:)=[L*(i-20),L*(i-19)];
ey(i,:)=[0,L];
end
end
%STIFFNESS MATRIX
K=zeros(28);
M=zeros(28);
for i=1:25
E=ep(1);A=ep(2);
xt=ex(i,2)-ex(i,1);
yt=ey(i,2)-ey(i,1);
L=sqrt(xt^2+yt^2);
l=xt/L; m=yt/L;
ke=E*A/L*[l^2 l*m -l^2 -l*m;
l*m m^2 -l*m -m^2;
-l^2 -l*m l^2 l*m;
-l*m -m^2 l*m m^2;];
m=L*A*rho;
me=[m/2 0 0 0;
0 m/2 0 0;
0 0 m/2 0;
0 0 0 m/2];
edoft=Edof(i,2:5);
K(edoft,edoft)=K(edoft,edoft)+ke;
M(edoft,edoft)=M(edoft,edoft)+me;
end
nd=size(K,1);
fdof=[1:nd]';
b=[1 15 16]';
fdof(b(:))=[];
[X,D]=eig(K(fdof,fdof),M(fdof,fdof));
nfdof=size(X,1);
eigenval=diag(D);
eigenvec=zeros(nd,nfdof);
eigenvec(fdof,:)=X;
eigenval1=eigenval(1)
eigenvec1=eigenvec(:,1)
eigenval2=eigenval(2)
eigenvec2=eigenvec(:,2)
eigenval3=eigenval(3)
eigenvec3=eigenvec(:,3)
t=Edof(:,2:5);
eignmode=eigenvec(:,2);
for i = 1:25
Edb(i,1:4)=eignmode(t(i,:))';
end
eldraw2(ex,ey)
The resulting egienpairs are:
Combining the images into a gif results in the following
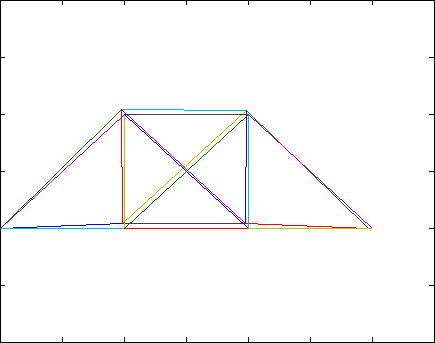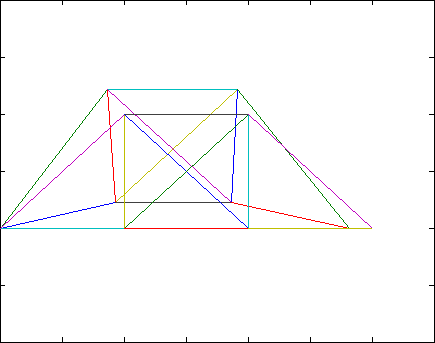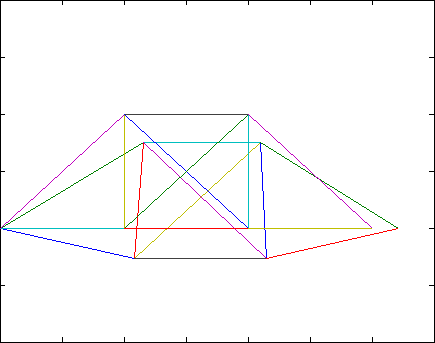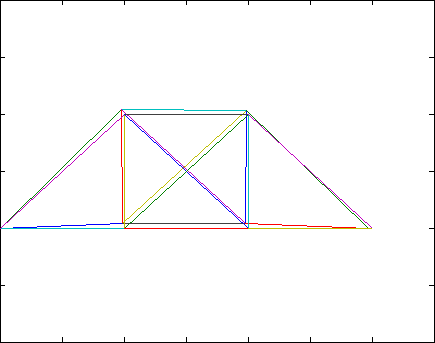
References
[edit | edit source]
Contributing Team Members
[edit | edit source]| Problem Assignments | ||
|---|---|---|
| Problem # | Solved & Typed by | Reviewed by |
| 1 | Kristin Howe | All |
| 2 | Joshua Plicque | All |
| 3 | Brandon Wright | All |
| 4 | Matthew Gidel,Spencer Herran | All |
On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.

































