TEAM 1: REPORT
Contents taken from Page 274 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664. Contents taken from Page 274 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664
Knowing that the magnitude of the horizontal force P is 8 kN, determine the stress at (a ) point A , (b ) point B . Honor Pledge: On my honor, I have neither given nor received unauthorized aid in doing this assignment.
We must first analyze the cross sectional area.
A
=
30
⋅
24
=
720
m
m
2
{\displaystyle A=30\cdot 24=720mm^{2}}
Next calculate the moment of inertia of the rectangular cross section.
I
=
b
d
3
12
=
30
⋅
24
3
12
=
34560
m
m
4
{\displaystyle I={\frac {bd^{3}}{12}}={\frac {30\cdot 24^{3}}{12}}=34560mm^{4}}
Next calculate the centroid of the rectangle
c
=
h
2
=
12
m
m
{\displaystyle c={\frac {h}{2}}=12mm}
Next we show a free body diagram of the forces present on the bracket
e
=
45
m
m
−
24
2
=
33
m
m
{\displaystyle e=45mm-{\frac {24}{2}}=33mm}
Calculate the bending couple using P = 8kN and e = 0.033m
M
=
P
e
=
8
⋅
0.033
=
264
N
∗
m
{\displaystyle M={\color {blue}Pe}=8\cdot 0.033=264N*m}
Now we can calculate the stresses
σ
c
e
n
t
r
i
c
=
−
P
A
=
8
⋅
10
3
7.2
⋅
10
−
4
=
−
11.11
M
P
a
{\displaystyle \sigma _{centric}={\color {blue}{\frac {-P}{A}}}={\frac {8\cdot 10^{3}}{7.2\cdot 10^{-4}}}=-11.11MPa}
σ
b
e
n
d
i
n
g
=
M
C
I
=
264
⋅
0.012
34560
⋅
10
(
−
3
)
4
=
90.67
M
P
a
{\displaystyle \sigma _{bending}={\color {blue}{\frac {MC}{I}}}={\frac {264\cdot 0.012}{34560\cdot 10^{\left(-3\right)^{4}}}}=90.67MPa}
Stress induced at point A:
σ
A
=
σ
c
e
n
t
r
i
c
−
σ
b
e
n
d
i
n
g
=
−
11.11
M
P
a
−
91.67
M
P
a
=
−
102.78
M
P
a
{\displaystyle \sigma _{A}=\sigma _{centric}-\sigma _{bending}=-11.11MPa-91.67MPa={\color {red}-102.78MPa}}
Stress induced at point B:
σ
B
=
σ
c
e
n
t
r
i
c
+
σ
b
e
n
d
i
n
g
=
−
11.11
M
P
a
+
91.67
M
P
a
=
80.56
M
P
a
{\displaystyle \sigma _{B}=\sigma _{centric}+\sigma _{bending}=-11.11MPa+91.67MPa={\color {red}80.56MPa}}
Contents taken from Page 274 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664. Contents taken from Page 274 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664
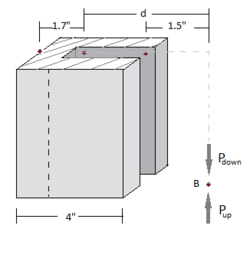
The vertical portion of the press of the press shown consists of a rectangular tube of wall thickness t = 8 mm. Knowing that the press has been tightened on wooden planks being glued together until P = 20 kN, determine the stress at (a ) point A , (b ) point B . Honor Pledge: On my honor, I have neither given nor received unauthorized aid in doing this assignment.
Given(s):
t
=
8
m
m
P
=
20
k
N
{\displaystyle t=8mm\,\,\,\,\,\,\,P=20kN}
Rectangular cutout is 64 mm x 44 mm
A
=
(
80
m
m
)
(
60
m
m
)
−
(
61
m
m
)
(
49
m
m
)
=
1.984
⋅
10
3
m
m
2
{\displaystyle A=(80mm)(60mm)-(61mm)(49mm)=1.984\cdot 10^{3}mm^{2}}
I
=
(
60
m
m
)
(
80
m
m
)
3
12
−
(
44
m
m
)
(
64
m
m
)
3
12
=
1.59881
⋅
10
6
m
m
2
=
1.599
⋅
10
−
6
m
4
{\displaystyle I={\frac {(60mm)(80mm)^{3}}{12}}-{\frac {(44mm)(64mm)^{3}}{12}}=1.59881\cdot 10^{6}mm^{2}=1.599\cdot 10^{-6}m^{4}}
c
=
40
m
m
=
0.004
m
{\displaystyle c=40mm=0.004m}
e
=
200
m
m
+
40
=
240
m
m
⟹
0.240
m
{\displaystyle e=200mm+40=240mm\implies 0.240m}
M
=
P
⋅
e
=
(
20
⋅
10
3
N
)
(
0.240
m
)
=
4.8
⋅
10
3
N
−
m
{\displaystyle {\color {blue}M=P\cdot e}=(20\cdot 10^{3}N)(0.240m)=4.8\cdot 10^{3}N-m}
Stress induced at point A:
σ
A
=
−
20
⋅
10
3
N
1.984
⋅
10
−
3
−
(
4.8
⋅
10
3
N
−
m
)
(
−
0.04
m
)
(
1.59881
⋅
10
−
6
m
)
=
130.240
⋅
10
6
P
a
{\displaystyle \sigma _{A}=-{\frac {20\cdot 10^{3}N}{1.984\cdot 10^{-3}}}-{\frac {(4.8\cdot 10^{3}N-m)(-0.04m)}{(1.59881\cdot 10^{-6}m)}}={\color {red}130.240\cdot 10^{6}Pa}}
Stress induced at point B:
σ
B
=
−
20
⋅
10
3
N
1.984
⋅
10
−
3
−
(
4.8
⋅
10
3
N
−
m
)
(
0.04
m
)
(
1.59881
⋅
10
−
6
m
)
=
−
110.0
⋅
10
6
P
a
{\displaystyle \sigma _{B}=-{\frac {20\cdot 10^{3}N}{1.984\cdot 10^{-3}}}-{\frac {(4.8\cdot 10^{3}N-m)(0.04m)}{(1.59881\cdot 10^{-6}m)}}\,={\color {red}-110.0\cdot 10^{6}Pa}}
Contents taken from Page 276 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664. * Contents taken from Page 276 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664. (*) = Reference to listed textbook
An offset h must be introduced into a metal tube of 0.75 in outer diameter and 0.08 in wall thickness. Knowing the maximum stress after the offset is introduced must not exceed 4 times the stress in the tube when it is straight, determine the largest offset that can be used. Honor Pledge: On my honor, I have neither given nor received unauthorized aid in doing this assignment.
GIVEN
Term
Desig
Value
Outer Diameter
d
o
{\displaystyle d_{o}}
0.75
i
n
{\displaystyle 0.75in}
Thickness
t
{\displaystyle t}
0.08
i
n
{\displaystyle 0.08in}
Inner Diameter
d
i
{\displaystyle d_{i}}
d
i
=
d
o
−
t
=
0.75
−
0.08
(
2
)
=
0.59
i
n
{\displaystyle d_{i}=d_{o}-t=0.75-0.08(2)=0.59in}
Area
A
{\displaystyle A}
π
4
(
d
o
2
−
d
i
2
)
=
π
4
(
0.75
2
−
0.59
2
)
≈
0.168
i
n
2
{\displaystyle {\frac {\pi }{4}}\left(d_{o}^{2}-d_{i}^{2}\right)={\frac {\pi }{4}}\left(0.75^{2}-0.59^{2}\right)\approx 0.168in^{2}}
Stress
σ
{\displaystyle \sigma }
σ
=
P
A
{\displaystyle \sigma ={\frac {P}{A}}}
The internal forces in the cross section are equivalent to a centric force P and a bending curve M. (*) Ex:4.07 on pg 272 EQ 4.49 on page 270(*) states:
F
=
P
M
=
P
d
{\displaystyle {\color {blue}F=P\,\,\,\,\,\,\,\,\,\,M=Pd}}
(Where F = Force at centroid, P = Line of action load, M = Moment, and d = offset distance.) EQ 4.5 on page 271(*) states:
σ
x
=
P
A
−
M
γ
I
{\displaystyle {\color {blue}\sigma _{x}={\frac {P}{A}}-{\frac {M\gamma }{I}}}}
γ
=
d
o
2
=
0.375
i
n
{\displaystyle \gamma ={\frac {d_{o}}{2}}=0.375in}
The Moment of Inertia of a Hollowed Cylindrical Cross-Section:
I
=
π
64
(
d
o
4
−
d
i
4
)
=
π
64
(
0.75
4
−
0.59
4
)
=
0.00958
i
n
4
{\displaystyle {\color {blue}I={\frac {\pi }{64}}\left(d_{o}^{4}-d_{i}^{4}\right)}={\frac {\pi }{64}}\left(0.75^{4}-0.59^{4}\right)=0.00958in^{4}}
To ensure the the max stress does not exceed 4 times the stress in the tube and making an assumption that P = 1, we can derive the following solution:
σ
a
l
l
=
4
σ
=
4
P
A
{\displaystyle \sigma _{all}=4\sigma =4{\frac {P}{A}}}
σ
a
l
l
=
P
A
−
M
γ
I
=
P
A
−
P
d
γ
I
{\displaystyle \sigma _{all}={\frac {P}{A}}-{\frac {M\gamma }{I}}={\frac {P}{A}}-{\frac {Pd\gamma }{I}}}
⟹
4
P
A
=
P
A
+
P
d
γ
I
⟹
4
A
=
1
A
+
d
γ
I
⟹
3
A
=
d
γ
I
{\displaystyle \implies 4{\frac {P}{A}}={\frac {P}{A}}+{\frac {Pd\gamma }{I}}\implies {\frac {4}{A}}={\frac {1}{A}}+{\frac {d\gamma }{I}}\implies {\frac {3}{A}}={\frac {d\gamma }{I}}}
⟹
3
0.168
=
d
(
0.375
)
0.00958
⟹
d
=
+
0.456
i
n
{\displaystyle \implies {\frac {3}{0.168}}={\frac {d(0.375)}{0.00958}}\implies d={\color {red}+0.456in}}
Contents taken from Page 276 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664. Contents taken from Page 276 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664. (*) = Reference to listed textbook
A vertical rod is attached at point A to the cast iron hanger shown. Knowing that the allowable stress in the hanger are
σ
a
l
l
=
+
5
k
s
i
{\displaystyle \sigma _{all}=+5ksi}
σ
a
l
l
=
−
12
k
s
i
{\displaystyle \sigma _{all}=-12ksi}
Honor Pledge: On my honor, I have neither given nor received unauthorized aid in doing this assignment.
Max allowable stresses on the hanger:
σ
a
l
l
o
w
=
+
5
k
s
i
{\displaystyle \sigma _{allow}=+5ksi}
F
m
a
x
↓
=
?
{\displaystyle F_{max\downarrow }=?}
σ
a
l
l
o
w
=
−
12
k
s
i
{\displaystyle \sigma _{allow}=-12ksi}
F
m
a
x
↑
=
?
{\displaystyle F_{max\uparrow }=?}
Take
y
¯
{\displaystyle {\overline {y}}}
Y
¯
=
∑
y
¯
A
∑
A
{\displaystyle {\overline {Y}}={\frac {\sum {\overline {y}}A}{\sum A}}}
A
1
=
(
3
i
n
)
(
1
i
n
)
=
3
i
n
2
{\displaystyle A_{1}=(3in)(1in)=3in^{2}}
A
2
=
(
3
i
n
)
(
.75
i
n
)
=
2.25
i
n
2
{\displaystyle A_{2}=(3in)(.75in)=2.25in^{2}}
A
3
=
A
2
=
2.25
i
n
2
{\displaystyle A_{3}=A_{2}=2.25in^{2}}
y
1
¯
=
1
2
i
n
=
.5
i
n
{\displaystyle {\overline {y_{1}}}={\frac {1}{2}}in=.5in}
y
2
¯
=
1
i
n
+
3
2
i
n
=
2.5
i
n
{\displaystyle {\overline {y_{2}}}=1in+{\frac {3}{2}}in=2.5in}
y
3
¯
=
y
2
¯
=
2.5
i
n
{\displaystyle {\overline {y_{3}}}={\overline {y_{2}}}=2.5in}
∴
Y
¯
=
(
.5
i
n
)
(
3
i
n
)
+
(
2.5
i
n
)
(
2.25
i
n
)
+
(
2.5
i
n
)
(
2.25
i
n
)
7.5
i
n
=
1.7
i
n
{\displaystyle \therefore {\overline {Y}}={\frac {(.5in)(3in)+(2.5in)(2.25in)+(2.5in)(2.25in)}{7.5in}}=1.7in}
Must incorporate the parallel axis theorem to find moment of inertia:
I
=
b
h
3
12
+
A
d
2
{\displaystyle {\color {blue}I={\frac {bh^{3}}{12}}+Ad^{2}}}
b = base, h = height, A = area, and d = perpendicular distance between centroidal axis and parallel axis
I
1
=
b
1
h
1
3
12
+
A
1
d
1
2
w
h
e
r
e
d
1
=
(
y
1
¯
−
Y
¯
)
⟹
I
1
=
(
3
i
n
)
(
1
i
n
)
3
12
+
(
3
i
n
2
)
(
.5
i
n
−
1.7
i
n
)
2
=
4.57
i
n
4
{\displaystyle {\color {blue}I_{1}={\frac {b_{1}h_{1}^{3}}{12}}+A_{1}d_{1}^{2}}\,\,where\,\,{\color {blue}d_{1}=({\overline {y_{1}}}-{\overline {Y}})}\implies I_{1}={\frac {(3in)(1in)^{3}}{12}}+(3in^{2})(.5in-1.7in)^{2}=4.57in^{4}}
I
2
=
b
2
h
2
3
12
+
A
2
d
2
2
w
h
e
r
e
d
2
=
(
y
2
¯
−
Y
¯
)
⟹
I
1
=
(
.75
i
n
)
(
3
i
n
)
3
12
+
(
2.25
i
n
2
)
(
2.5
i
n
−
1.7
i
n
)
2
=
3.1275
i
n
4
{\displaystyle {\color {blue}I_{2}={\frac {b_{2}h_{2}^{3}}{12}}+A_{2}d_{2}^{2}}\,\,where\,\,{\color {blue}d_{2}=({\overline {y_{2}}}-{\overline {Y}})}\implies I_{1}={\frac {(.75in)(3in)^{3}}{12}}+(2.25in^{2})(2.5in-1.7in)^{2}=3.1275in^{4}}
I
3
=
I
2
=
3.1275
i
n
4
{\displaystyle I_{3}=I_{2}=3.1275in^{4}}
∴
{\displaystyle \therefore }
I
T
o
t
=
I
1
+
I
2
+
I
3
=
4.57
i
n
4
+
3.1275
i
n
4
+
3.1275
i
n
4
⟹
10.825
i
n
4
{\displaystyle {\color {blue}I_{Tot}=I_{1}+I_{2}+I_{3}}=4.57in^{4}+3.1275in^{4}+3.1275in^{4}\implies 10.825in^{4}}
The normal stress at point A is due to bending:
σ
b
e
n
d
i
n
g
=
−
M
y
I
{\displaystyle {\color {blue}\sigma _{bending}=-{\frac {My}{I}}}}
"The internal forces in the cross section are equivalent to a centric force P and a bending couple M " (Example Problem 4.07 page 272(*))
M
=
P
d
P
=
F
m
a
x
=
m
a
x
i
m
u
m
f
o
r
c
e
d
=
{\displaystyle {\color {blue}M=Pd}\,\,\,\,\,{\color {blue}P=F_{max}=maximumforce}\,\,\,\,\,d=}
(EQ 4.49 page 270 (*)) Normal stress due to centric load:
σ
c
e
n
t
r
i
c
=
P
A
{\displaystyle {\color {blue}\sigma _{centric}={\frac {P}{A}}}}
σ
=
σ
c
e
n
t
r
i
c
+
σ
b
e
n
d
i
n
g
=
P
A
−
M
y
I
{\displaystyle {\color {blue}\sigma =\sigma _{centric}+\sigma _{bending}={\frac {P}{A}}-{\frac {My}{I}}}}
↑=
{\displaystyle \uparrow =}
Assuming conventions:
σ
m
a
x
=
+
5
k
s
i
,
A
=
7.5
i
n
2
,
I
=
10.825
i
n
4
,
y
=
−
1.7
i
n
,
d
{\displaystyle \sigma _{max}=+5ksi,A=7.5in^{2},I=10.825in^{4},y=-1.7in,d}
=
1.5
+
1.7
=
3.2
i
n
{\displaystyle =1.5+1.7=3.2in}
σ
m
a
x
=
P
m
a
x
A
−
M
y
I
=
P
m
a
x
A
−
P
m
a
x
d
y
I
=
P
m
a
x
(
1
A
−
d
y
I
)
{\displaystyle {\color {blue}\sigma _{max}={\frac {P_{max}}{A}}-{\frac {My}{I}}}={\frac {P_{max}}{A}}-{\frac {P_{max}dy}{I}}=P_{max}({\frac {1}{A}}-{\frac {dy}{I}})}
⟹
P
m
a
x
↓
=
σ
m
a
x
(
1
A
−
d
y
I
)
=
5
k
s
i
(
1
7.5
i
n
2
−
(
3.2
i
n
)
(
−
1.7
i
n
)
10.825
i
n
4
)
=
7.86
k
i
p
s
{\displaystyle \implies P_{max\downarrow }={\frac {\sigma _{max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}={\frac {5ksi}{({\frac {1}{7.5in^{2}}}-{\frac {(3.2in)(-1.7in)}{10.825in^{4}}})}}=7.86kips}
σ
a
l
l
=
−
12
k
s
i
,
A
=
7.5
i
n
2
,
I
=
10.825
i
n
4
,
y
=
4
−
1.7
=
2.3
i
n
,
d
=
1.5
+
1.7
=
3.2
i
n
{\displaystyle \sigma _{all}=-12ksi,\,A=7.5in^{2},\,I=10.825in^{4},\,y=4-1.7=2.3in,\,d=1.5+1.7=3.2in}
P
m
a
x
↑
=
σ
m
a
x
(
1
A
−
d
y
I
)
=
21.955
k
i
p
s
{\displaystyle P_{max\uparrow }={\frac {\sigma _{max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}=21.955kips}
The limiting factor is at 7.86 kips force upward. Apply negative sign throughout equation:
σ
m
a
x
=
−
P
m
a
x
A
−
−
m
y
I
⟹
P
m
a
x
=
−
σ
a
l
l
/
m
a
x
(
1
A
−
d
y
I
)
{\displaystyle {\color {blue}\sigma _{max}={\frac {-P_{max}}{A}}-{\frac {-my}{I}}\implies P_{max}={\frac {-\sigma _{all/max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}}}
The Downward force becomes:
σ
a
l
l
=
+
5
k
s
i
,
A
=
7.5
i
n
2
,
I
=
10.825
i
n
4
,
y
=
2.3
i
n
,
d
=
3.2
i
n
{\displaystyle \sigma _{all}=+5ksi,\,A=7.5in^{2},\,I=10.825in^{4},\,y=2.3in,\,d=3.2in}
⟹
P
m
a
x
↓
=
9.15
k
i
p
s
{\displaystyle \implies P_{max\downarrow }=9.15kips}
The Upward Force becomes:
σ
m
a
x
=
−
12
k
s
i
,
A
=
7.5
i
n
2
,
I
=
10.825
i
n
4
,
y
=
2.3
i
n
,
d
=
3.2
i
n
{\displaystyle \sigma _{max}=-12ksi,\,A=7.5in^{2},\,I=10.825in^{4},\,y=2.3in,\,d=3.2in}
⟹
P
m
a
x
↑
=
18.87
k
i
p
s
{\displaystyle \implies P_{max\uparrow }=18.87kips}
∴
{\displaystyle \therefore }
9.15
k
i
p
s
{\displaystyle {\color {red}9.15kips}}
Contents taken from Page 276 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664. Contents taken from Page 276 in the Mechanics of Materials: 6th Edition textbook. Authors: F.P BEER, E.R. JOHNSTON, J.T. DEWOLF AND D.F. MAZUREK ISBN:9780077565664
A vertical rod is attached at point B to the cast iron hanger shown. Knowing that the allowable stress in the hanger are
σ
a
l
l
=
+
5
k
s
i
{\displaystyle \sigma _{all}=+5ksi}
σ
a
l
l
=
−
12
k
s
i
{\displaystyle \sigma _{all}=-12ksi}
Honor Pledge: On my honor, I have neither given nor received unauthorized aid in doing this assignment.
3D Representation of Figure 4.115 Max allowable stresses on the hanger:
σ
a
l
l
o
w
=
+
5
k
s
i
{\displaystyle \sigma _{allow}=+5ksi}
F
m
a
x
↓
=
?
{\displaystyle F_{max\downarrow }=?}
σ
a
l
l
o
w
=
−
12
k
s
i
{\displaystyle \sigma _{allow}=-12ksi}
F
m
a
x
↑
=
?
{\displaystyle F_{max\uparrow }=?}
Take
y
¯
{\displaystyle {\overline {y}}}
Y
¯
=
∑
y
¯
A
∑
A
{\displaystyle {\overline {Y}}={\frac {\sum {\overline {y}}A}{\sum A}}}
A
1
=
(
3
i
n
)
(
1
i
n
)
=
3
i
n
2
{\displaystyle A_{1}=(3in)(1in)=3in^{2}}
A
2
=
(
3
i
n
)
(
.75
i
n
)
=
2.25
i
n
2
{\displaystyle A_{2}=(3in)(.75in)=2.25in^{2}}
A
3
=
A
2
=
2.25
i
n
2
{\displaystyle A_{3}=A_{2}=2.25in^{2}}
y
1
¯
=
1
2
i
n
=
.5
i
n
{\displaystyle {\overline {y_{1}}}={\frac {1}{2}}in=.5in}
y
2
¯
=
1
i
n
+
3
2
i
n
=
2.5
i
n
{\displaystyle {\overline {y_{2}}}=1in+{\frac {3}{2}}in=2.5in}
y
3
¯
=
y
2
¯
=
2.5
i
n
{\displaystyle {\overline {y_{3}}}={\overline {y_{2}}}=2.5in}
∴
Y
¯
=
(
.5
i
n
)
(
3
i
n
)
+
(
2.5
i
n
)
(
2.25
i
n
)
+
(
2.5
i
n
)
(
2.25
i
n
)
7.5
i
n
=
1.7
i
n
{\displaystyle \therefore {\overline {Y}}={\frac {(.5in)(3in)+(2.5in)(2.25in)+(2.5in)(2.25in)}{7.5in}}=1.7in}
Must incorporate the parallel axis theorem to find moment of inertia:
I
=
b
h
3
12
+
A
d
2
{\displaystyle {\color {blue}I={\frac {bh^{3}}{12}}+Ad^{2}}}
b = base, h = height, A = area, and d = perpendicular distance between centroidal axis and parallel axis
I
1
=
b
1
h
1
3
12
+
A
1
d
1
2
w
h
e
r
e
d
1
=
(
y
1
¯
−
Y
¯
)
⟹
I
1
=
(
3
i
n
)
(
1
i
n
)
3
12
+
(
3
i
n
2
)
(
.5
i
n
−
1.7
i
n
)
2
=
4.57
i
n
4
{\displaystyle {\color {blue}I_{1}={\frac {b_{1}h_{1}^{3}}{12}}+A_{1}d_{1}^{2}}\,\,where\,\,{\color {blue}d_{1}=({\overline {y_{1}}}-{\overline {Y}})}\implies I_{1}={\frac {(3in)(1in)^{3}}{12}}+(3in^{2})(.5in-1.7in)^{2}=4.57in^{4}}
I
2
=
b
2
h
2
3
12
+
A
2
d
2
2
w
h
e
r
e
d
2
=
(
y
2
¯
−
Y
¯
)
⟹
I
1
=
(
.75
i
n
)
(
3
i
n
)
3
12
+
(
2.25
i
n
2
)
(
2.5
i
n
−
1.7
i
n
)
2
=
3.1275
i
n
4
{\displaystyle {\color {blue}I_{2}={\frac {b_{2}h_{2}^{3}}{12}}+A_{2}d_{2}^{2}}\,\,where\,\,{\color {blue}d_{2}=({\overline {y_{2}}}-{\overline {Y}})}\implies I_{1}={\frac {(.75in)(3in)^{3}}{12}}+(2.25in^{2})(2.5in-1.7in)^{2}=3.1275in^{4}}
I
3
=
I
2
=
3.1275
i
n
4
{\displaystyle I_{3}=I_{2}=3.1275in^{4}}
∴
{\displaystyle \therefore }
I
T
o
t
=
I
1
+
I
2
+
I
3
=
4.57
i
n
4
+
3.1275
i
n
4
+
3.1275
i
n
4
⟹
10.825
i
n
4
{\displaystyle {\color {blue}I_{Tot}=I_{1}+I_{2}+I_{3}}=4.57in^{4}+3.1275in^{4}+3.1275in^{4}\implies 10.825in^{4}}
The normal stress at point A is due to bending:
σ
b
e
n
d
i
n
g
=
−
M
y
I
{\displaystyle {\color {blue}\sigma _{bending}=-{\frac {My}{I}}}}
"The internal forces in the cross section are equivalent to a centric force P and a bending couple M " (Example Problem 4.07 page 272(*))
M
=
P
d
P
=
F
m
a
x
=
m
a
x
i
m
u
m
f
o
r
c
e
d
=
{\displaystyle {\color {blue}M=Pd}\,\,\,\,\,{\color {blue}P=F_{max}=maximumforce}\,\,\,\,\,d=}
(EQ 4.49 page 270 (*)) Normal stress due to centric load:
σ
c
e
n
t
r
i
c
=
P
A
{\displaystyle {\color {blue}\sigma _{centric}={\frac {P}{A}}}}
σ
=
σ
c
e
n
t
r
i
c
+
σ
b
e
n
d
i
n
g
=
P
A
−
M
y
I
{\displaystyle {\color {blue}\sigma =\sigma _{centric}+\sigma _{bending}={\frac {P}{A}}-{\frac {My}{I}}}}
↑=
{\displaystyle \uparrow =}
Assuming conventions:
σ
m
a
x
=
+
5
k
s
i
,
A
=
7.5
i
n
2
,
I
=
10.825
i
n
4
,
y
=
+
2.3
i
n
,
d
{\displaystyle \sigma _{max}=+5ksi,A=7.5in^{2},I=10.825in^{4},y=+2.3in,d}
=
3.2
i
n
{\displaystyle =3.2in}
σ
m
a
x
=
P
m
a
x
A
−
M
y
I
=
P
m
a
x
A
−
P
m
a
x
d
y
I
=
P
m
a
x
(
1
A
−
d
y
I
)
{\displaystyle {\color {blue}\sigma _{max}={\frac {P_{max}}{A}}-{\frac {My}{I}}}={\frac {P_{max}}{A}}-{\frac {P_{max}dy}{I}}=P_{max}({\frac {1}{A}}-{\frac {dy}{I}})}
⟹
P
m
a
x
↓
=
σ
m
a
x
(
1
A
−
d
y
I
)
=
5
k
s
i
(
1
7.5
i
n
2
−
(
3.8
i
n
)
(
−
2.3
i
n
)
10.825
i
n
4
)
=
6.15
k
i
p
s
{\displaystyle \implies P_{max\downarrow }={\frac {\sigma _{max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}={\frac {5ksi}{({\frac {1}{7.5in^{2}}}-{\frac {(3.8in)(-2.3in)}{10.825in^{4}}})}}={\color {Red}6.15kips}}
Largest upward force: Apply negative sign throughout equation:
σ
m
a
x
=
−
P
m
a
x
A
−
−
m
y
I
⟹
P
m
a
x
=
−
σ
a
l
l
/
m
a
x
(
1
A
−
d
y
I
)
{\displaystyle {\color {blue}\sigma _{max}={\frac {-P_{max}}{A}}-{\frac {-my}{I}}\implies P_{max}={\frac {-\sigma _{all/max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}}}
σ
a
l
l
=
+
5
k
s
i
,
A
=
7.5
i
n
2
,
I
=
10.825
i
n
4
,
y
=
−
1.7
i
n
,
d
=
3.2
i
n
{\displaystyle \sigma _{all}=+5ksi,\,A=7.5in^{2},\,I=10.825in^{4},\,y=-1.7in,\,d=3.2in}
P
m
a
x
↑
=
σ
m
a
x
(
1
A
−
d
y
I
)
=
13.54
k
i
p
s
{\displaystyle P_{max\uparrow }={\frac {\sigma _{max}}{({\frac {1}{A}}-{\frac {dy}{I}})}}={\color {Red}13.54kips}}
Egm3520.s13.Jeandona (discuss • contribs ) 12:47, 10 April 2013 (UTC)