Talk:QB/d Bell.polarization/components

• 
  component
• 
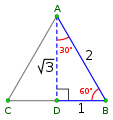
  30-60-90 triangle
• 
  45-45-90 triangle

The component, or vector projection of the vector A along a direction parallel to B is obtained by dropping a perpendicular to the line defined by B and measuring the length of side labeled $|A|\cos \theta$ as shown above. Note that the length of B is not important here. In application to polarization, the length and direction of A represents the electric field, and B indicates the direction of the polarizing filter.

It is easily verified that both triangles shown obey the Pythagorean theorem. Students should be able to draw from memory two pairs of right triangles with the following lengths:

$1:1:{\sqrt {2}}{\text{ and }}{\tfrac {1}{\sqrt {2}}}:{\tfrac {1}{\sqrt {2}}}:1{\text{ (for 45-45-90 degree triangle)}}$

$1:2:{\sqrt {3}}{\text{ and }}{\tfrac {1}{2}}:{\tfrac {\sqrt {3}}{2}}:1{\text{ (for 30-60-90 degree triangle)}}$

To verify the Pythagorean theorem:

${\begin{aligned}1^{2}+1^{2}=({\sqrt {2}})^{2}&{\text{, and }}&({\tfrac {1}{\sqrt {2}}})^{2}+({\tfrac {1}{\sqrt {2}}})^{2}={\tfrac {1}{2}}+{\tfrac {1}{2}}=1\\1^{2}+({\sqrt {3}})^{2}=2^{2}&{\text{, and }}&({\tfrac {1}{2}})^{2}+({\tfrac {\sqrt {3}}{2}})^{2}={\tfrac {1}{4}}+{\tfrac {3}{4}}=1\end{aligned}}$

Note that at the moment, all the questions inform you that the passage of energy goes as the component squared (since energy is porportional to electric field squared...something students don't need to memorize. Our goal is to teach scientific literacy, not scientific facts in a conceptual physics course.

Start a discussion about QB/d Bell.polarization/components

Talk pages are where people discuss how to make content on Wikiversity the best that it can be. You can use this page to start a discussion with others about how to improve QB/d Bell.polarization/components.

Start a discussion