Talk:QB/d Bell.Venn
1
[edit source]- 2/4=1/2 - 2/5 + 3/5 - 3/4 - 5/6
Hint
[edit source](2+1)/5 = 3/5 (Add dots in the α and Δ regions)
2
[edit source]- 2/4=1/2 + 2/5 - 3/5 - 3/4 - 5/6
Hint
[edit source](1+1)/5=2/5 add dots in the β and Δ regions
3
[edit source]- 4/5 - 5/6 - 5/4 - 6/5 + 7/5
Hint
[edit source](5+2)/5=7/5 Add the dots, and then add twice the center. Or add the dots outside the Δ region, and then add three times what is in the Δ region (since it gets counted thrice).
4
[edit source]- −2/5 - −1/5 - 0 + +1/5 - +2/5 - +1
Hint
[edit source]P(spade,diamond)=3/5 and C=2P-1 = +1/5= {3(same)−2(different)}/5
5
[edit source]- −2/5 + −1/5 - 0 - +1/5 - +2/5 - +1
Hint
[edit source]
6
[edit source]
- 0 - 1/4 + 1/2 - 3/4 - 1 - 5/4
Hint
[edit source]2 and 4 are even
7
[edit source]
- 0 - 1/4 - 1/2 + 3/4 - 1 - 5/4
Hint
[edit source]2, 3, and 5 are prime
8
[edit source]
- 0 - 1/4 - 1/2 - 3/4 - 1 + 5/4
Hint
[edit source]P(even)+P(prime)= 2/4 + 3/4 = 5/4
9
[edit source]
- 0 + 1/4 - 1/2 - 3/4 - 1 - 5/4
Hint
[edit source]Only 2 is both prime and even
10
[edit source]
- 0 - 1/4 - 1/2 - 3/4 + 1 - 5/4
Hint
[edit source]Every number is either: the first is boty, the second is odd, the third is even, and the fourth is odd (whew!)
Raw script
[edit source]- t QB/d_Bell.Venn
- ! CC0 user:Guy vandegrift
- ?
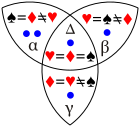
P(♠,♦) = ?
Assume the dots represent five observations. - - 2/4=1/2
- - 2/5
- + 3/5
- - 3/4
- - 5/6
- $ (2+1)/5 = 3/5 (Add dots in the α and Δ regions)
- ! CC0 user:Guy vandegrift
- ?

P(♠,♥) = ?
Assume the dots represent five observations. - - 2/4=1/2
- + 2/5
- - 3/5
- - 3/4
- - 5/6
- $ (1+1)/5=2/5 add dots in the β and Δ regions
- ! CC0 user:Guy vandegrift
- ?

P(♠,♦)+P(♠,♥)+P(♥,♦) = ?
Assume the dots represent five observations. - -4/5
- -5/6
- -5/4
- -6/5
- +7/5
- $ (5+2)/5=7/5 Add the dots, and then add twice the center. Or add the dots outside the Δ region, and then add three times what is in the Δ region (since it gets counted thrice).
- ! CC0 user:Guy vandegrift
- ?
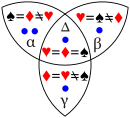
C(♠,♦) = ?
Assume the dots represent five observations. - - −2/5
- - −1/5
- - 0
- + +1/5
- - +2/5
- - +1
- $P(spade,diamond)=3/5 and C=2P-1 = +1/5= {3(same)−2(different)}/5
- ! CC0 user:Guy vandegrift
- ?

C(♠,♥) = ?
Assume the dots represent five observations. - - −2/5
- + −1/5
- - 0
- - +1/5
- - +2/5
- - +1
- $
- ! CC0 user:Guy vandegrift
- ?

- - 0
- - 1/4
- + 1/2
- - 3/4
- - 1
- - 5/4
- $ 2 and 4 are even
- ! CC0 user:Guy vandegrift
- ?

- - 0
- - 1/4
- - 1/2
- + 3/4
- - 1
- - 5/4
- $ 2, 3, and 5 are prime
- ! CC0 user:Guy vandegrift
- ?

- - 0
- - 1/4
- - 1/2
- - 3/4
- - 1
- + 5/4
- $ P(even)+P(prime)= 2/4 + 3/4 = 5/4
- ! CC0 user:Guy vandegrift
- ?

- - 0
- + 1/4
- - 1/2
- - 3/4
- - 1
- - 5/4
- $ Only 2 is both prime and even
- ! CC0 user:Guy vandegrift
- ?

- - 0
- - 1/4
- - 1/2
- - 3/4
- + 1
- - 5/4
- $ Every number is either: the first is boty, the second is odd, the third is even, and the fourth is odd (whew!)



