Strength of materials/Lesson 1
Lesson 1: Stress and strain
[edit | edit source]In this lesson we will review the concepts of stress and strain and suggest some improvements over the definitions from elementary strength of materials.
Stress
[edit | edit source]In elementary strength of materials we define the stress () as
where is the resisting force and is the area on which it acts. From Newtons third Law, it is easy to see that resisting force is same as that of the force applied. If the resisting force is not same as that of the force applied then we are supposed to take the resisting force value. For ex. Water is almost incompressible. So resisting force it offers is Zero (as it moves sideways or in some other possible direction). Then the Stress acting is Zero as the resisting force is Zero..What are the assumptions that we make when we use this definition? Some of the assumptions made are:
- The body is homogeneous, i.e., it is made of the same material in all its parts.
- The body is isotropic, i.e., the properties of the material do not depend on direction.
- The cross section is constant.
- The body is straight.
- The load is applied axially along the center line of the body, etc.
In essence, we assume that the body is a one-dimensional rod. Even in that situation we are implicitly saying that the stress is just an average over the whole body.
A better way to think about stress is as a point quantity. If we can do that then we can deal with bodies that have different stresses at different points - which is what one sees in real life. So how do we go about defining such a point stress?
What we do is to imagine a tiny block of material inside the body and then define the stresses in that tiny block. Such a block is more commonly known as an infinitesimal element of the body.
In an infinitesimal element of a body, we can assume that the stresses are constant (because they don't change much over the length of the element). We can also resolve any applied force into components that act normal and tangential to the faces of the element. And we can choose the element to be such that the cross section is constant. So we can meet all the requirements of the elementary strength of materials definition of stress while making it applicable for each point in a body.
 |
The updated definition of stress is
We have just chosen the area on which the force acts to be so small that we can think of the stress as acting at a point.
Types of Stresses
[edit | edit source]Since there can be both normal and tangential components of force acting on the infinitesimal element, we can have normal stresses and shear stresses acting on the element. Suppose that we call the normal component and the shear component . Then the normal stress is defined as
and the shear stress () is defined as
What are the units of stress? Since the units of force may be "lbf" or "N" and the units of area may be "in" or "m", the units of stress may be
Now let us consider a rod under uniaxial tension. The question is, is there a shear stress in the bar?
In fact, there is always a orientation inside the bar along which there is a shear stress though it may not look like it. You can see that this is indeed the case by taking a section along the bar that is inclined at an angle less that 90 to the axis. In that case, the applied force can be resolved into components and normal and tangential to the section. Clearly, that indicates that there has to be a shear stress in the bar. If you do an experiment in the lab and pull on a bar until it breaks, you will often see that the fracture surface is inclined to the direction of application of force. This indicates that there is a shear stress in the bar.
 |
This suggests an important point. You have to know the orientation of the infinitesimal element to find the critical stress in a body.
Stress components at a point
[edit | edit source]Since an infinitesimal element has six faces, we can resolve the applied force into components in each of the faces. By convention, we resolve the applied force into components along the directions of the coordinate axis. Since there are three axes in three dimensions there will be three such force components on each face giving a total of 18 forces on the element.
For equilibrium of forces we need forces acting in opposite directions to be equal. That reduces the number of unique force components to 9 with three normal force components and six shear force components. Also, from the balance of moments, we can show that the shear force components acting on planes perpendicular to the coordinate axes must be of equal magnitude. There are three such planes and hence the number of unique shear force components reduces to three.
You can get a feel for the situation by looking at the adjacent figure. There are three normal stresses corresponding to the three normal forces. These are labeled , , and where the subscript indicates the plane on which the normal force acts.
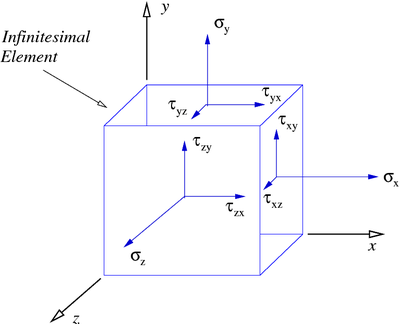 |
The three shear stresses are , , and where the first subscript indicates the plane on which the shear forces acts and the second indicates the direction of the force.
From moment equilibrium, we have
The three things to note at this point are:
- Stress is a point quantity and varies from point to point.
- The stress depends on the orientation.
- The stress has six components.
Strain
[edit | edit source]In elementary strength of materials, the strain is defined as the change in length over the original length.
Just as we did for the stress, we can define the strain as a point quantity by choosing a small element and allowing the initial length of that element to go to zero. Thus our new definition of strain is
Types of Strain
[edit | edit source]To retain the parallelism with stresses we have to define normal strains and shear strains.
The normal strains indicate how much line segments in the infinitesimal element in the , , directions change. These strains are labeled , , and .
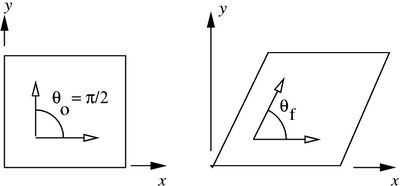
The shear strains indicate the change in angle of a right angle initially in the , , and planes. These angles are measured in radians and the strains are labelled , and . The adjacent figure shows how shear strain is measured in the plane. In this case
 |
The units of strain are dimensionless. However, people often write strain in terms of or . Since strains are small for most engineering applications (between 1 and 2 percent), people often use microstrains so that they don't have to deal with tiny numbers.
It is a bit confusing that the normal strains deal with changes in length while the shear strains deal with changes in angle. In fact, all strains deal with changes in length. However, for the very small strains that we find in engineering, the change in length due to shear and the change in angle are approximately the same. For a more accurate descriptions of strains you can look at the courses on Introduction to Elasticity or Continuum mechanics.





































