Spectroscopy/Rotational spectroscopy

Subject classification: this is a chemistry resource.

Type classification: this is a lesson resource.

• A molecule can store energy in its tumbling motion.
• This is only relevant in the gas phase where molecules are in continual motion and are free to rotate unhindered.
• Rotational motion at the molecular level is quantized in accordance with quantum mechanical theory.
• Transitions between discrete rotational energy levels give rise to the rotational spectrum of the molecule (microwave spectroscopy).

We will study:

• classical rotational motion, angular momentum, rotational inertia
• quantum mechanical energy levels
• selection rules and microwave (rotational) spectroscopy
• the extension to polyatomic molecules

Classical rotational motion

Rotational energy is kinetic energy associated with a tumbling motion.

Consider a particle with mass m, rotating with angular velocity ω, at a distance R from a given axis.

• This particle has angular momentum J
• |J| = I ω where |J| is the magnitude of the angular momentum vector, and I is the moment of inertia (the rotational equivalent of mass).

Where do we use rotational spectroscopy? The 2.45 GHz frequency used by microwave ovens is the most ideal one for causing water molecules to rotate at their fastest possible rate. There is also the added bonus that this frequency is not used for communication, so microwave ovens do not interfere with cell phones, wireless internet, televisions and so on.

Diatomic molecules: the rigid rotor

Remember that a molecule does not distort under rotation.

Diatomic molecules: the rigid rotor

R = r₁ + r₂ (Eq. 1)

The axis passes through the centre of mass (C):

$m_{1}r_{1}=m_{2}r_{2}$ (Eq. 2)

Moment of inertia:

$I=\sum _{i}m_{i}r_{i}^{2}=m_{1}r_{1}^{2}+m_{2}r_{2}^{2}$ (Eq. 3)

Using equations 1, 2 and 3:

$I={\frac {m_{1}m_{2}}{(m_{1}+m_{2})}}R^{2}$
$I=\mu R^{2}$	$\mu ={\frac {m_{1}m_{2}}{(m_{1}+m_{2})}}$

μ is the reduced mass.

Example: For ¹H³⁵Cl - $\mu ={\frac {1{\mbox{u}}\times 35{\mbox{u}}}{(1{\mbox{u}}+35{\mbox{u}})}}={\frac {35}{36}}{\mbox{u}}=1.61\times 10^{-27}{\mbox{kg}}$ (Remember that u = atomic mass unit = 1.661x10^-27 kg)

Rotational energy levels

Classical: $E={\begin{matrix}{\frac {1}{2}}\end{matrix}}I\omega ^{2}={\frac {|J|^{2}}{2I}}$

Quantum mechanical: solve the Schrödinger equation for the rigid diatomic rotor.

$E_{J}={\frac {h^{2}}{8\pi ^{2}I}}J(J+1)$

• E_J is measured in Joules
• J is the rotational quantum number (= 0, 1, 2, ...)

Converted to wavenumbers:	Rotational constant:
$\varepsilon _{J}={\frac {E_{J}}{hc}}=BJ(J+1)$	$B={\frac {h}{8\pi ^{2}Ic}}$

• The units of ε_J and B = cm^-1

Below are the rotational energy levels for diazenylium, N₂H⁺.

N2H+ rotational energy levels

	N2H+
J = 0 → εJ = 0	0
J = 1 → εJ = 2B cm-1	≈3 cm-1
J = 2 → εJ = 6B cm-1	≈10 cm-1

Important points to notice:

• The energy of the ground state (J = 0) is zero - because the molecule is not rotating.
• As J increases, the molecules rotate more and more quickly - as a result, the energy levels are more widely spaced apart.
• The energy level separations are compatible with the microwave region of the EM spectrum.

But what about spectroscopic transitions between energy levels? And what about the selection rules for microwave spectroscopy?

Gross selection rule

Gross Selection Rule: The requirement for a permanent dipole.

For example, take a rotating HCl molecule. The fluctuation in its dipole component has an identical form to the fluctuation in the electric field of EM radiation (see the electromagnetic wave in Lesson 1).

As a result, the electric field of the EM wave exerts a torque on the dipole of the HCl molecule.

This means that energy can be absorbed or emitted, giving rise to a rotational spectrum.

Gross Selection Rule: molecules with permanent dipoles are microwave active (the molecule must be polar), e.g. heteronuclear diatomics - HCl, CO, NO, etc. Homonuclear diatomics are microwave inactive (e.g. O2, N2, etc.) In other words, a dipole must be present in the molecule for you to get a rotational spectrum.

Transitions between energy levels

Specific Selection Rule: During a transition, the rotational quantum number must change by 1 unit only, i.e. ΔJ = ±1 (angular momentum is conserved)

In other words, only transitions between neighboring energy levels are possible.

Below is an example rotational spectrum.

Example rotational spectrum

$\Delta \varepsilon =\varepsilon _{J+1}-\varepsilon _{J}=B(J+1)(J+2)-BJ(J+1)$

$\Delta \varepsilon =2B(J+1){\mbox{cm}}^{-1}$

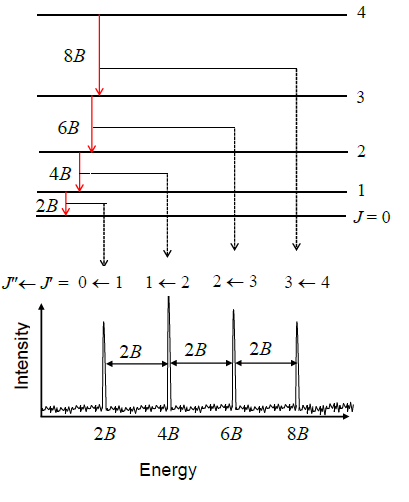
The top part shows the rotational energy levels, ε_J. The bottom part shows the microwave spectrum as observed from an experiment.

Each absorption (red arrow) complies with ΔJ = +1.

As a result of the equations in the box above, you get a series of spectral lines, each separated by 2B.

For CO, Δε = 3.86 cm^-1. For HCl, Δε = 21.18 cm^-1.

You'd get the same values for emission spectroscopy, except ΔJ = -1.

After obtaining a microwave spectrum from experiment, you measure n_exp in cm^-1. (The distance between spectral lines is Δn_exp). From this you can work the rotational constant B, because Δv_exp (this is the intensity of each spectral line) = 2B. Using the formulae in the green boxes further up this page you can work out B and I. Now you can calculate molecular properties (such as R, μ) to a high degree of accuracy.

Rotational energy level population

Note that the most intense band is not the first line in the spectrum. Why?

Remember the 3 factors from Lesson 1:

1. Amount of sample
2. Population of energy states
3. Selection rules

We need to consider number 2 - the Boltzmann distribution AND degeneracy.

${\frac {N_{f}}{N_{i}}}={\frac {g_{f}}{g_{i}}}\exp \left(-{\frac {\Delta E}{k_{B}T}}\right)$

N_f and N_i are the population of molecules in energy levels e_f and e_i with degeneracy g_fand g_I.

From quantum mechanics, the degeneracy of each e_J level = 2J + 1

J = 0	1 (non-degenerate)
J = 1	3 (3-fold degenerate)
J = 2	5 (5-fold degenerate)
J = 3	7 (7-fold degenerate)

Population of excited state relative to ground state:

Initial state:	J = 0	ei = e0 = 0	gi = g0 = 1
Final state:	J	ef = eJ = BJ(J + 1)	gf = (2J+1)

Δε = ε_J - ε₀ = BJ(J + 1) →

${\frac {N_{J}}{N_{0}}}=(2J+1)\exp \left(-{\frac {BJ(J+1)}{k_{B}T}}\right)$

Example for J = 1 (at T = 300 K):

B = 2 cm-1	Nf/Ni = 2.94
B = 10 cm-1	Nf/Ni = 2.70

The population of the J = 1 level decreases as the energy level separation (i.e. 2B) increases.

Degeneracy (the pre-exponential term) moves the maximum population away from J = 0. You can use calculus to determine the most populated level - the maximum which occurs when ${\frac {dN_{J}}{dJ}}=0$.

${\begin{matrix}{\frac {dN_{J}}{dJ}}&=&N_{0}\left\{2e^{-{\frac {BJ(J+1)}{k_{B}T}}}+(2J+1)e^{-{\frac {BJ(J+1)}{k_{B}T}}}\left[-{\frac {B(2J+1)}{k_{B}T}}\right]\right\}\\\ &=&N_{0}e^{-{\frac {BJ(J+1)}{k_{B}T}}}\left[2+(2J+1)\left(-{\frac {B(2J+1)}{k_{B}T}}\right)\right]=0\\\ &\ &2+(2J+1)^{2}\left(-{\frac {B}{k_{B}T}}\right)=0\to (2J+1)^{2}={\frac {2k_{B}T}{B}}\\\ &\ &{\Bigg \Downarrow }\end{matrix}}$

$J_{max}={\sqrt {\frac {k_{B}T}{2B}}}-{\frac {1}{2}}$

For example, at 300K, B = 5 cm^-1 → k_BT = 208.5 cm^-1 → J_max = 4 (which corresponds to the 4→5 transition).

Non-rigid rotor

Gray text is additional information provided for further reading only. This content will not be tested.

We have assumed so far that the bond length remains fixed during rotation of the molecule - this is the rigid rotor model. However, as the molecule rotates the atoms are subject to centrifugal forces which stretch the bonds - this is the non-rigid rotor model.

Hooke's law states for an elastic bond:

$F=-k(r-r_{eq})$

$k=4\pi ^{2}\omega ^{2}c^{2}m$

• F = restoring force (N)
• r = bond length; r_eq = equilibrium bond length (m)
• k = force constant (Nm^-1)
• c = vibrational frequency (cm^-1)
• m = reduced mass (kg)

Non-rigid rotor model for diatomic molecules:

Non-rigid rotor model for diatomic molecules	Centrifugal distortion coefficient
$\varepsilon _{J}=BJ(J+1)-DJ^{2}(J+1)^{2}$	$D={\frac {h^{3}}{32\pi ^{4}I^{2}R^{2}kc}}$

The first term is the rigid rotor model, and the second term is a correction for the centrifugal distortion. It is important to consider this for high values of J.

Centrifugal distortion leads to lowering of the given energy level (at high J). Consequently, spectral lines cluster together at high J and are no longer equally spaced.

Polyatomic molecules

The majority of molecules are not diatomic - they can possess rotation around more than one axis.

The classical expression for energy of a body rotating about axis a is $E_{a}={\begin{matrix}{\frac {1}{2}}\end{matrix}}I\omega ^{2}={\frac {J_{a}^{2}}{2I_{a}}}$

With similar expressions for the other axes, it follows that:

$E_{total}={\frac {J_{a}^{2}}{2I_{a}}}+{\frac {J_{b}^{2}}{2I_{b}}}+{\frac {J_{c}^{2}}{2I_{c}}}$

Polyatomic molecules are categorised according to their moments of inertia about 3 perpendicular axes:

• Linear - one moment of inertia equals zero: I_a = I_b, I_c = 0. Molecules include CO₂, OCS, C₂H₂.
• Spherical rotor - three equal moments of inertia: I_a = I_b = I_c. Molecules include CH₄, SiH₄, SF₆.
• Symmetric rotor - two equal moments of inertia: I_a = I_b ≠ I_c. Molecules include NH₃, CH₃Cl, CH₃CN.
• Asymmetric rotor - three different moments of inertia: I_a ≠ I_b ≠ I_c. Molecules include H₂O, CH₃OH, H₂CO.

Calculation of B: Example Calculate the value of the rotational constant B for a molecule of carbon monoxide. The bond length (R) of CO is 0.113 nm. Solutions Step 1: Calculate the reduced mass using equation $\mu ={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}$. $\mu ={\frac {12{\mbox{u}}16{\mbox{u}}}{(12{\mbox{u}}+16{\mbox{u}})}}={\frac {192}{28}}{\mbox{u}}=1.14\times 10^{-26}{\mbox{kg}}$ Step 2: Calculate the moment of inertia using equation $I=\mu R^{2}$. $I=(1.14\times 10^{-26}{\mbox{kg}})\times (0.113\times 10^{-9}{\mbox{m}})^{2}=1.46\times 10^{-46}{\mbox{kg m}}^{2}$ Step 3: Calculate the rotational constant using equation $B={\frac {h}{8\pi ^{2}Ic}}$. $B={\frac {(6.626\times 10^{-34}{\mbox{Js}})}{8\pi ^{2}\times (1.46\times 10^{-46}{\mbox{kg m}}^{2})\times (2.99\times 10^{10}{\mbox{cm s}}^{-1})}}=1.93{\mbox{cm}}^{-1}$ Notice that a low m and a low R give a high B.

Lesson 3. Vibrational Spectroscopy