Spectroscopy/Molecular energy levels
| Subject classification: this is a chemistry resource. |
| Type classification: this is a lesson resource. |
Molecular spectroscopy is the study of the interaction of electromagnetic (EM) radiation with matter. It is based on the analysis of EM radiation that is emitted, absorbed, or scattered by molecules, which can give information on:
- chemical analysis (finding a chemical fingerprint, so to speak)
- molecular structure (bond lengths, angles, strengths, energy levels, etc...)
Types of molecular energy
[edit | edit source]Energy can be stored either as potential energy or kinetic energy, in a variety of ways including:
- Translational energy: small amounts of energy stored as kinetic energy. This is unquantized (can take any value) and hence is not relevant to spectroscopy.
- Rotational energy: kinetic energy associated with the tumbling motion of molecules. This is quantized.
- Vibrational energy: the oscillatory motion of atoms or groups within a molecule (potential energy ↔ kinetic energy exchange). This is quantized.
- Electronic energy: energy stored as potential energy in excited electronic configurations. This is quantized.
|
This results in a series of molecular energy levels. Spectroscopy is the measuring of the transitions between levels. |
Typical values for energy level separations
[edit | edit source]
Energies (and wavefunctions) for these different levels are obtained from quantum mechanics by solving the Schrödinger equation. Spectroscopy is used to interrogate these different energy levels.
Electromagnetic radiation
[edit | edit source]
Electromagnetic (EM) radiation consists of photons (elementary particles) which behave as both particles and waves.
The image to the right shows the wave-like character associated with a single photon of EM radiation.
- In the x,z plane there is an oscillating electric field (E)
- In the y,z plane there is an oscillating magnetic field (B)
Both are in phase but perpendicular to each other.
Key equations
[edit | edit source]- c = speed of light (2.998x108 ms-1)
- λ = wavelength (m)
- ν = frequency (s-1)
- = wavenumber (m-1)
Transitions between energy levels
[edit | edit source]
- Absorption spectroscopy: a photon is absorbed ("lost") as the molecule is raised to a higher energy level.
- Emission spectroscopy: a photon is emitted ("created") as the molecule falls back to a lower energy level.
Electromagnetic spectrum
[edit | edit source]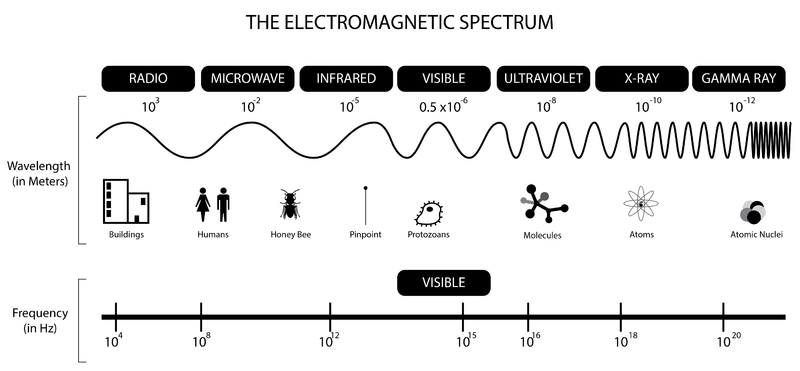
Relevant regions for this course:
- Radio → nuclear spin in magnetic field
- Microwave → rotation
- Infrared → vibration
- Ultraviolet → electronic
Common units in spectroscopy
[edit | edit source]Wavelength, λ
- S.I. unit = metres (m)
- Other units = micrometer (1 μm = 10-6 m) ; nanometer (1 nm = 10-9 m) ; Angstrom (1 Å = 10-10 m)
Frequency, ν
- S.I. unit = Hertz (Hz) or s-1
- Other units = megahertz (1 MHz = 106 Hz) ; gigahertz (1 GHz = 109 Hz)
Energy, E
- S.I. unit = Joules (J)
- For molar energies, multiply by Avogadro's constant (NA) = J mol-1 or kJ mol-1
Wavenumber,
- S.I. unit = m-1
- Units of cm-1 are most commonly used in spectroscopy
- Molecular spectra are typically recorded as line intensities as a function of frequency, wavelength or wavenumber.
- Remember the importance of using correct units and being able to convert between different ones (see the formulae below).
Factors influencing intensity of spectral lines
[edit | edit source]1. Amount of sample
The intensity of lines on the spectrum will be affected by the amount of sample which light passes through. The intensity of this transmitted light depends on the sample concentration and path length.
- Beer-Lambert Law
2. Population of energy states
A system can undergo a transition from one level, i, to another level, f, but only if it is in the first level i to begin with.
- Boltzmann Distribution
3. Spectroscopic selection rules
A selection rule is a statement about which potential transitions are allowed and which are forbidden. Each spectroscopy has its own selection rules (see later lessons). Not all transitions are allowed even though energy conservation is obeyed.
1. Amount of sample
[edit | edit source]Absorbance and transmittance
[edit | edit source]| Beer-Lambert Law: | |
| Absorbance (A) | |
| Transmittance (T) | |
- ε = molar absorption coefficient
- units of ε: conc-1 x length-1 (usually mol-1 dm3 cm-1)
- incident light intensity.
- transmitted light intensity.
- L = path length (in cm)
- εmax is the maximum absorption coefficient, and is an indication of the intensity of a transition.
2. Population of energy states
[edit | edit source]The continuous thermal agitation that molecules experience at any temperature (greater than zero Kelvin) ensures that they are distributed over all possible energy levels.
- Population of a state = the average number of molecules in a state at any given time.

The mathematical formulation of how to calculate the population of a state was provided by Ludwig Boltzmann in the late 19th century.
The Boltzmann distribution
[edit | edit source]The Boltzmann distribution defines the relative population of energy states (usually the ratio of excited states to ground state).
- kB = Boltzmann constant (= R / NA) = 1.381x10-23 J K-1
- T = temperature (Kelvin)
Effect of temperature
[edit | edit source]The Boltzmann distribution is a continuous function.
|
There is always a higher population in a state of lower energy than in one of higher energy. |
At lower temperatures, the lower energy states are more greatly populated. At higher temperatures, there are more higher energy states populated, but each is populated less.
Effect of energy separation
[edit | edit source]kBT NA ~ 2.5 kJ mol-1 at 300 K.

- Rotational:
- Vibrational:
- Electronic:
Degeneracy
[edit | edit source]Degeneracy = when more than one state has the same energy.
- gi and gf = degeneracies of initial and final states
This is very important for rotational energy levels (see later). As a result, the population of an energy state is then a product of the Boltzmann distribution and the degeneracy.
- This means that the ground state may no longer be the most populated state.
|
Population of Energy Levels: Example
Assuming that the vibrational energy levels of HCl and I2 are equally spaced, with energy separations of 2990.94 and 216.51 cm-1 respectively, calculate for each case the ratio of the number of molecules in the first two vibrational states relative to the ground state at T = 300 K and 800 K.
|
3. Spectroscopic selection rules
[edit | edit source]Each spectroscopy has its own selection rules, which will be covered later in the course.
|
|





























