Selected topics in finite mathematics/Eulerian cycles

An Eulerian Cycle is a cycle in a graph which contains every edge.

Objectives

Use every edge exactly once.

Details

A graph is connected if there is a path between any two vertices. If in a graph every vertex has an even number of edges incident upon it, the graph will have a Eulerian cycle.

A graph has an Eulerian Cycle if and only if all vertices have even numbers of edges. If a graph can't make an Eulerian Cycle, the process to make it a Eulerian Cycle is called Eulerizing.

A eulerian cycle is especially useful when trying to optimize paths and routes. For example, these cycles would be used when designing routes for trash collection, checking parking meters etc. Using a Eulerian cycle would allow one to save time by only walking down each street or pathway one time.

Examples

Figure E1: A graph with edges labeling an Eulerian Cycle.

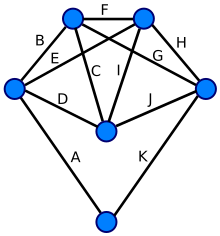
1. The graph given in figure E1 is an Eulerian graph. Its edges are labelled with an Eulerian Cycle: A-B-C-D-E-F-G-H-I-J-K

Nonexamples

1. In figure E1, A-B-C-I-H-K is not an Eulerian cycle because it misses an edge (several, in fact).

FAQ

Q: How do you know where to place new edges when you are trying to Eulerize an graph?
A: Add edges to all the vertices with odd degree, until every vertex has even degree. There are multiple ways to Eulerize a graph, some will be more efficient than others.

Homework

Figure H1

1. Find an Eulerian cycle in the graph given in figure H1.