Robotic Mechanics and Modeling/Kinematics

Introduction to Kinematics for Robotic Mechanics and Modeling (Portion from Link)

Inverse kinematics of SCARA robot done with MeKin2D.

Kinematics is the science and math of describing the configuration, position, velocity, and acceleration of an object or a machine. We ignore the dynamics or changes in velocity/acceleration due to inertia of the machine. We also ignore internal or external forces that may be acting on the machine.

Robot kinematics applies geometry to the study of the movement of multi-degree of freedom kinematic chains that form the structure of robotic systems. The emphasis on geometry means that the links of the robot are modeled as rigid bodies and its joints are assumed to provide pure rotation or translation.

Robot kinematics studies the relationship between the dimensions and connectivity of kinematic chains and the position, velocity and acceleration of each of the links in the robotic system, in order to plan and control movement and to compute actuator forces and torques.

Motion along a Line (1-D)

Position in 1-D

In 1-D, we can imagine the position of a particle along a line given as $x_{i}$, and this position is not subject to rotation but can only move along the line (translate) to a new position $x_{f}$.

Velocity in 1-D

In 1-D, we can describe the change in position ${\boldsymbol {x}}$ (a translation) over time $t$ as a velocity ${\boldsymbol {v}}$ (a vector with speed and direction) without accounting for rotation and angular velocity:

${\boldsymbol {v}}=\operatorname {d} \!{\boldsymbol {x}}/\operatorname {d} \!t$

A familiar expression for describing position motion from $x_{i}$ to $x_{f}$ as a function of time with constant speed $v_{c}$ is:

$x_{f}=x_{i}+v_{c}t$

Acceleration in 1-D

In 1-D, we can describe the change in velocity ${\boldsymbol {v}}$ (a translation) over time $t$ as an acceleration ${\boldsymbol {a}}$ (a vector with speed and direction) without accounting for rotation, angular velocity, or acceleration:

${\boldsymbol {a}}=\operatorname {d} \!{\boldsymbol {v}}/\operatorname {d} \!t$

Motion from $x_{i}$ to $x_{f}$ as a function of time with constant speed $v_{c}$ and constant acceleration $a_{c}$ is:

$x_{f}=x_{i}+v_{c}t+{\frac {1}{2}}a_{c}t^{2}$

Example for 1-D Motion in IPython (JupyterLab)

An example of how to setup a symbolic expression ${\textstyle x_{f}=x_{i}+v_{c}t+{\frac {1}{2}}a_{c}t^{2}}$ in IPython.

Code

%reset -f
from sympy import symbols
x_f,x_i,v_c,a_c,t = symbols('x_f x_i v_c a_c t')
x_f=x_i+v_c*t+1/2*a_c*t*t
x_f

If $x_{i}=0$, $v_{c}=1\,\mathrm {m/s}$, and $a_{c}=1\,\mathrm {m/s^{2}}$, what is $x_{f}$ after 1 second?

Code

x_f=x_f.subs(x_i,0)
x_f=x_f.subs(v_c,1)
x_f=x_f.subs(a_c,1)
x_f=x_f.subs(t,1)
x_f

The answer is 1.5 $\mathrm {m}$.

Additional Examples of 1-D Kinematics

Additional Examples of 1-D Kinematics

Kinematics of a particle trajectory in a non-rotating frame of reference (Copied and edited from Kinematics)

Kinematic quantities of a classical particle: mass m, position r, velocity v, acceleration a.

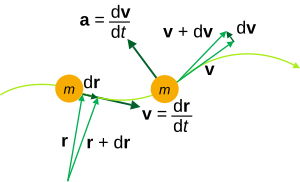
Representation of Vectors and Paths

Particle kinematics is the study of the trajectory of particles. The position of a particle is defined as the coordinate vector from the origin of a coordinate frame to the particle. In the most general case, a three-dimensional coordinate system is used to define the position of a particle. However, if the particle is constrained to move within a plane, a two-dimensional coordinate system is sufficient. All observations in physics are incomplete without being described with respect to a reference frame.

The position vector of a particle is a vector drawn from the origin of the reference frame to the particle. It expresses both the distance of the point from the origin and its direction from the origin. In three dimensions, the position of point P can be expressed as

$\mathbf {P} =<x_{P},y_{P},z_{P}>=x_{P}{\hat {\imath }}+y_{P}{\hat {\jmath }}+z_{P}{\hat {k}},$

where $x_{P}$, $y_{P}$, and $z_{P}$ are the Cartesian coordinates and ${\hat {\imath }}$, ${\hat {\jmath }}$ and ${\hat {k}}$ are the unit vectors along the $x$, $y$, and $z$ coordinate axes, respectively. The magnitude of the position vector $\left|\mathbf {P} \right|$ gives the distance between the point $\mathbf {P}$ and the origin.

$|\mathbf {P} |={\sqrt {x_{P}^{\ 2}+y_{P}^{\ 2}+z_{P}^{\ 2}}}.$

The direction cosines of the position vector provide a quantitative measure of direction. It is important to note that the position vector of a particle isn't unique. The position vector of a given particle is different relative to different frames of reference.

The trajectory of a particle is a vector function of time, $\mathbf {P} (t)$, which defines the curve traced by the moving particle, given by

$\mathbf {P} (t)=x_{P}(t){\hat {\imath }}+y_{P}(t){\hat {\jmath }}+z_{P}(t){\hat {k}},$

where the coordinates x_P, y_P, and z_P are each functions of time.

An Example for Representing a Position Vector in IPython

An example of how to define a "vector" $\mathbf {P} =<1,2,3>$ as an array in IPython.

Code

%reset -f
import numpy as np
P=np.array([1,2,3])

An example of how to calculate the magnitude of vector $\mathbf {P}$.

Code

MagnP=np.linalg.norm(P) #one approach
MagnP=np.dot(P,P)**0.5 #another approach

An example of how to plot the vector $\mathbf {P}$.

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

P=np.array([1,2,3])
# We don't know where P starts. We can place it at the origin
# and think of P as having U,V,W.
Porigin=np.array([0,0,0,P[0],P[1],P[2]])
print(Porigin)

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(Porigin[0],Porigin[1],Porigin[2],Porigin[3],
          Porigin[4],Porigin[5],pivot='tail',normalize=False)
ax.set_xlim([-3, 3])
ax.set_ylim([-3, 3])
ax.set_zlim([-3, 3])

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.view_init(20,-45)
plt.savefig('vector123in3D.png', bbox_inches='tight')

3D representation of Vector $\mathbf {P} <1,2,3>$.

An Example of Representing a 2D Path in IPython

Let's represent a trajectory with vector path $\mathbf {P} (t)=x_{P}(t){\hat {\imath }}+y_{P}(t){\hat {\jmath }}$, where $x_{P}(t)=t$ and $y_{P}(t)=e^{-t}\cos(2\pi t)$. Then, we can use the following code to represent this path of this trajectory.

Code

# See https://matplotlib.org/3.1.1/tutorials/introductory/
# pyplot.html#sphx-glr-tutorials-introductory-pyplot-py
# for instructions on 2D plotting
%reset -f
import numpy as np
import matplotlib.pyplot as plt

def x_p(t):
    return t

def y_p(t):
    return np.exp(-t) * np.cos(2*np.pi*t)

t1=np.arange(0,5,0.1)
t2=np.arange(0,5,0.02)

plt.figure()
plt.plot(x_p(t1),y_p(t1),'bo',x_p(t2),y_p(t2),'k')
plt.title('2D Path of $P(t)$',size=20)
plt.xlabel('$x_p(t)$')
plt.ylabel('$y_p(t)$')

# You can save a png of the produced plot by pressing 
# shift + right click.

plt.savefig('Path_xp_yp.png', dpi=300, bbox_inches='tight')

2D Path of $\mathbf {P} =x_{p}(t){\hat {\imath }}+y_{p}(t){\hat {\jmath }}$ for $x_{p}(t)=t$ and $y_{p}(t)=e^{-t}\cos(2\pi t)$.

Additional Examples for Vectors

Additional Examples for Vectors

The distance travelled is always greater than or equal to the displacement.

Velocity and speed

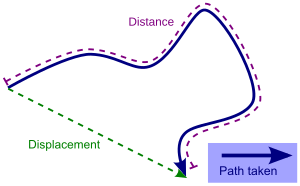
The velocity of a particle is a vector quantity that describes the magnitude as well as direction of motion of the particle. More mathematically, the rate of change of the position vector of a point, with respect to time is the velocity of the point. Consider the ratio formed by dividing the difference of two positions of a particle by the time interval. This ratio is called the average velocity over that time interval and is defined as Velocity=displacement/time taken

${\overline {\mathbf {V} }}={\frac {\Delta \mathbf {P} }{\Delta t}}\ ,$

where ΔP is the change in the position vector over the time interval Δt.

In the limit as the time interval Δt becomes smaller and smaller, the average velocity becomes the time derivative of the position vector,

$\mathbf {V} =\lim _{\Delta t\rightarrow 0}{\frac {\Delta \mathbf {P} }{\Delta t}}={\frac {d\mathbf {P} }{dt}}={\dot {\mathbf {P} }}={\dot {x}}_{p}{\hat {\imath }}+{\dot {y}}_{P}{\hat {\jmath }}+{\dot {z}}_{P}{\hat {k}}.$

Thus, velocity is the time rate of change of position of a point, and the dot denotes the derivative of those functions x, y, and z with respect to time. Furthermore, the velocity is tangent to the trajectory of the particle at every position the particle occupies along its path. Note that in a non-rotating frame of reference, the derivatives of the coordinate directions are not considered as their directions and magnitudes are constants.

The speed of an object is the magnitude |V| of its velocity. It is a scalar quantity:

$|\mathbf {V} |=|{\dot {\mathbf {P} }}|={\frac {ds}{dt}},$

where s is the arc-length measured along the trajectory of the particle. This arc-length traveled by a particle over time is a non-decreasing quantity. Hence, ds/dt is non-negative, which implies that speed is also non-negative.

Acceleration

The velocity vector can change in magnitude and in direction or both at once. Hence, the acceleration accounts for both the rate of change of the magnitude of the velocity vector and the rate of change of direction of that vector. The same reasoning used with respect to the position of a particle to define velocity, can be applied to the velocity to define acceleration. The acceleration of a particle is the vector defined by the rate of change of the velocity vector. The average acceleration of a particle over a time interval is defined as the ratio.

${\overline {\mathbf {A} }}={\frac {\Delta \mathbf {V} }{\Delta t}}\ ,$

where ΔV is the difference in the velocity vector and Δt is the time interval.

The acceleration of the particle is the limit of the average acceleration as the time interval approaches zero, which is the time derivative,

$\mathbf {A} =\lim _{\Delta t\rightarrow 0}{\frac {\Delta \mathbf {V} }{\Delta t}}={\frac {d\mathbf {V} }{dt}}={\dot {\mathbf {V} }}={\dot {v}}_{x}{\hat {\imath }}+{\dot {v}}_{y}{\hat {\jmath }}+{\dot {v}}_{z}{\hat {k}}$

or

$\mathbf {A} ={\ddot {\mathbf {P} }}={\ddot {x}}_{p}{\hat {\imath }}+{\ddot {y}}_{P}{\hat {\jmath }}+{\ddot {z}}_{P}{\hat {k}}$

Thus, acceleration is the first derivative of the velocity vector and the second derivative of the position vector of that particle. Note that in a non-rotating frame of reference, the derivatives of the coordinate directions are not considered as their directions and magnitudes are constants.

The magnitude of the acceleration of an object is the magnitude |A| of its acceleration vector. It is a scalar quantity:

$|\mathbf {A} |=|{\dot {\mathbf {V} }}|={\frac {dv}{dt}},$

Additional Examples for Velocity and Acceleration

Additional Examples for Velocity and Acceleration

Relative position vector

A relative position vector is a vector that defines the position of one point relative to another. It is the difference in position of the two points. The position of one point A relative to another point B is simply the difference between their positions

$\mathbf {P} _{A/B}=\mathbf {P} _{A}-\mathbf {P} _{B}$

which is the difference between the components of their position vectors.

If point A has position components $\mathbf {P} _{A}=<X_{A},Y_{A},Z_{A}>$

If point B has position components $\mathbf {P} _{B}=<X_{B},Y_{B},Z_{B}>$

then the position of point A relative to point B is the difference between their components: $\mathbf {P} _{A/B}=\mathbf {P} _{A}-\mathbf {P} _{B}=<X_{A}-X_{B},Y_{A}-Y_{B},Z_{A}-Z_{B}>$

Relative velocity

Main resource: Relative velocity

Relative velocities between two particles in classical mechanics.

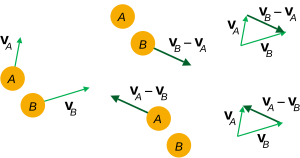
The velocity of one point relative to another is simply the difference between their velocities

$\mathbf {V} _{A/B}=\mathbf {V} _{A}-\mathbf {V} _{B}$

which is the difference between the components of their velocities.

If point A has velocity components $\mathbf {V} _{A}=<V_{A_{x}},V_{A_{y}},V_{A_{z}}>$

and point B has velocity components $\mathbf {V} _{B}=<V_{B_{x}},V_{B_{y}},V_{B_{z}}>$

then the velocity of point A relative to point B is the difference between their components: $\mathbf {V} _{A/B}=\mathbf {V} _{A}-\mathbf {V} _{B}=<V_{A_{x}}-V_{B_{x}},V_{A_{y}}-V_{B_{y}},V_{A_{z}}-V_{B_{z}}>$

Alternatively, this same result could be obtained by computing the time derivative of the relative position vector R_B/A.

In the case where the velocity is close to the speed of light c (generally within 95%), another scheme of relative velocity called rapidity, that depends on the ratio of V to c, is used in special relativity.

Relative acceleration

The acceleration of one point C relative to another point B is simply the difference between their accelerations.

$\mathbf {A} _{C/B}=\mathbf {A} _{C}-\mathbf {A} _{B}$

which is the difference between the components of their accelerations.

If point C has acceleration components $\mathbf {A} _{C}=<A_{C_{x}},A_{C_{y}},A_{C_{z}}>$

and point B has acceleration components $\mathbf {A} _{B}=<A_{B_{x}},A_{B_{y}},A_{B_{z}}>$

then the acceleration of point C relative to point B is the difference between their components: $\mathbf {A} _{C/B}=\mathbf {A} _{C}-\mathbf {A} _{B}=<A_{C_{x}}-A_{B_{x}},A_{C_{y}}-A_{B_{y}},A_{C_{z}}-A_{B_{z}}>$

Alternatively, this same result could be obtained by computing the second time derivative of the relative position vector P_B/A.

Rotation Matrix (Copied and edited from Rotation Matrix)

One of the key tools used to help in the representation of robotic pose, configuration, and orientation is the rotation matrix. In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix

$R={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}$

rotates points in the xy-plane counterclockwise through an angle θ with respect to the x axis about the origin of a two-dimensional Cartesian coordinate system. To perform the rotation on a plane point with standard coordinates v = (x,y), it should be written as column vector, and multiplied by the matrix R:

$R{\textbf {v}}\ =\ {\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}\cdot {\begin{bmatrix}x\\y\end{bmatrix}}\ =\ {\begin{bmatrix}x\cos \theta -y\sin \theta \\x\sin \theta +y\cos \theta \end{bmatrix}}.$

The examples in this article apply to active rotations of vectors counterclockwise in a right-handed coordinate system (y counterclockwise from x) by pre-multiplication (R on the left). If any one of these is changed (such as rotating axes instead of vectors, a passive transformation), then the inverse of the example matrix should be used, which coincides with its transpose.

Since matrix multiplication has no effect on the zero vector (the coordinates of the origin), rotation matrices describe rotations about the origin. Rotation matrices provide an algebraic description of such rotations, and are used extensively for computations in geometry, physics, and computer graphics. In some literature, the term rotation is generalized to include improper rotations, characterized by orthogonal matrices with determinant −1 (instead of +1). These combine proper rotations with reflections (which invert orientation). In other cases, where reflections are not being considered, the label proper may be dropped. The latter convention is followed in this article.

Rotation matrices are square matrices, with real entries. More specifically, they can be characterized as orthogonal matrices with determinant 1; that is, a square matrix R is a rotation matrix if and only if R^T = R⁻¹ and det R = 1. The set of all orthogonal matrices of size n with determinant +1 forms a group known as the special orthogonal group SO(n), one example of which is the rotation group SO(3). The set of all orthogonal matrices of size n with determinant +1 or −1 forms the (general) orthogonal group O(n).

Rotations in Two Dimensions

A counterclockwise rotation of a vector through angle θ. The vector is initially aligned with the x-axis.

In two dimensions, the standard rotation matrix has the following form,

$R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}$.

This rotates column vectors by means of the following matrix multiplication,

${\begin{bmatrix}x'\\y'\\\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}{\begin{bmatrix}x\\y\\\end{bmatrix}}$.

For example, if the vector $\mathbf {\hat {x}} ={\begin{bmatrix}1\\0\\\end{bmatrix}}$ is rotated by an angle $\theta$, its new coordinates are ${\begin{bmatrix}\cos \theta \\\sin \theta \\\end{bmatrix}}$

and if the vector $\mathbf {\hat {y}} ={\begin{bmatrix}0\\1\\\end{bmatrix}}$ is rotated by an angle $\theta$, its new coordinates are ${\begin{bmatrix}-\sin \theta \\\cos \theta \\\end{bmatrix}}$

More generally, the new coordinates (x′, y′) of the point (x, y) after rotation are

${\begin{aligned}x'&=x\cos \theta -y\sin \theta \,\\y'&=x\sin \theta +y\cos \theta \,\end{aligned}}$.

The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. −90°). Thus the clockwise rotation matrix is found as

$R(-\theta )={\begin{bmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{bmatrix}}\,$.

The two-dimensional case is the only non-trivial (i.e. not one-dimensional) case where the rotation matrices group is commutative, so that it does not matter in which order multiple rotations are performed. An alternative convention uses rotating axes, and the above matrices also represent a rotation of the axes clockwise through an angle θ.

An Example of Rotating a Vector in Two Dimensions with IPython

We will create a 2D rotation matrix to provide a rotation of $45^{o}$ to the vector $<1,0>$ at the origin.

Code

# https://matplotlib.org/gallery/images_contours_and_fields/quiver_simple_demo.html#sphx-glr-gallery-images-contours-and-fields-quiver-simple-demo-py
%reset -f
import matplotlib.pyplot as plt
import numpy as np

theta=np.pi/4
R=np.array([[np.cos(theta),-np.sin(theta)],[np.sin(theta),np.cos(theta)]])
print("Rotation Matrix R:")
print(R)

Vector=np.array([[1,0]])
Vector=Vector.T
print("Column Vector V:")
print(Vector)

RotatedVector=np.dot(R,Vector)
print("Rotated Vector:")
print(RotatedVector)

fig=plt.figure()
ax=fig.add_subplot(111)
ax.quiver(0,0,Vector[0],Vector[1],scale=4)
ax.set_xlim([-2, 2])
ax.set_ylim([-2, 2])
ax.quiver(0,0,RotatedVector[0],RotatedVector[1],scale=4,color='r')
ax.set_xlabel('X',size=20)
ax.set_ylabel('Y',size=20)
plt.savefig('2D_rotation_45_deg_vector10.png', dpi=300, bbox_inches='tight')

Counterclockwise rotation of vector $<1,0>$ by $45^{o}$ about the origin in two dimensions.

Rotations in Three Dimensions

See also: [[:Rotation Formalisms in Three Dimensions]]

Basic rotations

A basic rotation (also called elemental rotation) is a rotation about one of the axes of a coordinate system. The following three basic rotation matrices rotate vectors by an angle θ about the x-, y-, or z-axis, in three dimensions, using the right-hand rule—which codifies their alternating signs. (The same matrices can also represent a clockwise rotation of the axes.)

${\begin{alignedat}{1}R_{x}(\theta )&={\begin{bmatrix}1&0&0\\0&\cos \theta &-\sin \theta \\[3pt]0&\sin \theta &\cos \theta \\[3pt]\end{bmatrix}}\\[6pt]R_{y}(\theta )&={\begin{bmatrix}\cos \theta &0&\sin \theta \\[3pt]0&1&0\\[3pt]-\sin \theta &0&\cos \theta \\\end{bmatrix}}\\[6pt]R_{z}(\theta )&={\begin{bmatrix}\cos \theta &-\sin \theta &0\\[3pt]\sin \theta &\cos \theta &0\\[3pt]0&0&1\\\end{bmatrix}}\end{alignedat}}$

For column vectors, each of these basic vector rotations appears counterclockwise when the axis about which they occur points toward the observer, the coordinate system is right-handed, and the angle θ is positive. R_z, for instance, would rotate toward the y-axis a vector aligned with the x-axis, as can easily be checked by operating with R_z on the vector (1,0,0):

$R_{z}(90^{\circ }){\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}\cos 90^{\circ }&-\sin 90^{\circ }&0\\\sin 90^{\circ }&\quad \cos 90^{\circ }&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}0\\1\\0\\\end{bmatrix}}$

This is similar to the rotation produced by the above-mentioned two-dimensional rotation matrix. See below for alternative conventions which may apparently or actually invert the sense of the rotation produced by these matrices.

General rotations

Other rotation matrices can be obtained from these three using matrix multiplication. For example, the product

$R=R_{z}(\alpha )\,R_{y}(\beta )\,R_{x}(\gamma )$

represents a fixed-body rotation whose yaw, pitch, and roll angles are α, β and γ, respectively. More formally, it is an intrinsic rotation whose Tait–Bryan angles/Euler angles are α, β, γ, about axes z, y, x, respectively. Similarly, the product

$R=R_{z}(\gamma )\,R_{y}(\beta )\,R_{x}(\alpha )$

represents an extrinsic spaced-fixed rotation whose rotation angles are α, β, γ, about axes x, y, z.

These matrices produce the desired effect only if they are used to premultiply column vectors, and (since in general matrix multiplication is not commutative) only if they are applied in the specified order (see Ambiguities for more details).

An Example of a Single Rotation of a Vector in Three Dimensions

Create a 3D rotation matrix to provide a rotation of $45^{o}$ about the Z-axis to the vector $<1,0,0>$ at the origin.

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np


theta=np.pi/4
Rz=np.array([[np.cos(theta),-np.sin(theta),0],
            [np.sin(theta),np.cos(theta),0], 
            [0,0,1]])
print("Rotation Matrix Rz:")
print(Rz)

Vector=np.array([[1,0,0]])
Vector=Vector.T
print("Column Vector V:")
print(Vector)

Rv=np.dot(Rz,Vector)
print("Rotated Vector:")
print(Rv)

MagnVector=np.dot(Vector.T,Vector)**0.5
MagnRv=np.dot(Rv.T,Rv)**0.5
print("Magnitude of the original vector:",MagnVector[0][0])
print("Magnitude of the rotated vector:",MagnRv[0][0])

VectorOrigin=np.array([0,0,0,Vector[0],Vector[1],Vector[2]])
RvOrigin=np.array([0,0,0,Rv[0],Rv[1],Rv[2]])

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(VectorOrigin[0],VectorOrigin[1],VectorOrigin[2],
          VectorOrigin[3],VectorOrigin[4],VectorOrigin[5],
          pivot='tail',normalize=False)
ax.quiver(RvOrigin[0],RvOrigin[1],RvOrigin[2],
          RvOrigin[3],RvOrigin[4],RvOrigin[5],
          pivot='tail',color='red',normalize=False)
ax.set_xlim([0, 1])
ax.set_ylim([0, 1])
ax.set_zlim([0, 1])

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.view_init(30,-115)
plt.savefig('RotatedVector100in3D.png', bbox_inches='tight')

A vector $<1,0,0>$ rotated by $45^{o}$ about the Z-axis.

An Example of Successive XYZ Space-fixed Rotations of a Vector in Three Dimensions

Successive XYZ space-fixed rotations of vector $<1,0,0>$ at the origin of $90^{o}$ about X, then about Y, and then about Z.

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np


alpha=90*np.pi/180 #Space-fixed rotation (x)
beta=90*np.pi/180 #Space-fixed rotation (y)
gamma=90*np.pi/180 #Spac-fixed rotation (z)

Rx=np.array([[1,0,0],
             [0,np.cos(alpha),-np.sin(alpha)],
             [0,np.sin(alpha),np.cos(alpha)]])
Ry=np.array([[np.cos(beta),0,np.sin(beta)],
             [0,1,0],
             [-np.sin(beta),0,np.cos(beta)]])
Rz=np.array([[np.cos(gamma),-np.sin(gamma),0],
             [np.sin(gamma),np.cos(gamma),0], 
             [0,0,1]])

V=np.array([[1,0,0]])
V=V.T
print("Column Vector V:")
print(V)

RxV=np.dot(Rx,V)
RyxV=np.dot(Ry,RxV)
RzyxV=np.dot(Rz,RyxV)


VOrigin=np.array([0,0,0,V[0],V[1],V[2]])
RxVOrigin=np.array([0,0,0,RxV[0],RxV[1],RxV[2]])
RyxVOrigin=np.array([0,0,0,RyxV[0],RyxV[1],RyxV[2]])
RzyxVOrigin=np.array([0,0,0,RzyxV[0],RzyxV[1],RzyxV[2]])

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(VOrigin[0],VOrigin[1],VOrigin[2],
          VOrigin[3],VOrigin[4],VOrigin[5],
          pivot='tail',normalize=False)
ax.quiver(RxVOrigin[0],RxVOrigin[1],RxVOrigin[2],
          RxVOrigin[3],RxVOrigin[4],RxVOrigin[5],
          pivot='tail',color='red',normalize=False)
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.set_zlim([-1, 1])

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Original Vector and RxV(Red) Overalap')
ax.view_init(30,-115)
plt.savefig('XYZSpaceFixedRotations100X.png',bbox_inches='tight',dpi=300)

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(RxVOrigin[0],RxVOrigin[1],RxVOrigin[2],
          RxVOrigin[3],RxVOrigin[4],RxVOrigin[5],
          pivot='tail',normalize=False)
ax.quiver(RyxVOrigin[0],RyxVOrigin[1],RyxVOrigin[2],
          RyxVOrigin[3],RyxVOrigin[4],RyxVOrigin[5],
          pivot='tail',color='red',normalize=False)
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.set_zlim([-1, 1])

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('RxV(Blue) + RyxV(Red)')
ax.view_init(30,-130)
plt.savefig('XYZSpaceFixedRotations100XY.png',bbox_inches='tight',dpi=300)

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(RyxVOrigin[0],RyxVOrigin[1],RyxVOrigin[2],
          RyxVOrigin[3],RyxVOrigin[4],RyxVOrigin[5],
          pivot='tail',normalize=False)
ax.quiver(RzyxVOrigin[0],RzyxVOrigin[1],RzyxVOrigin[2],
          RzyxVOrigin[3],RzyxVOrigin[4],RzyxVOrigin[5],
          pivot='tail',color='red',normalize=False)
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.set_zlim([-1, 1])

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('RyxV(Blue) and RzyxV(Red) Overlap')
ax.view_init(30,-115)
plt.savefig('XYZSpaceFixedRotations100Final.png',bbox_inches='tight',dpi=300)

Original vector $<1,0,0>$ rotated $90^{o}$ about the X-axis has the same orientation.

Original vector $<1,0,0>$ rotated about X and then Y by $90^{o}$ each time.

Penultimate and resulting vector with space-fixed XYZ successive rotations.

An Example of Successive ZYX Body-fixed, Euler Rotations of a Vector in Three Dimensions

Successive ZYX space-fixed rotations of vector $<1,0,0>$ at the origin of $90^{o}$ about Z, then about Y', and then about X''. The final axes are given by x,y,z.

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np


alpha=90*np.pi/180 #Yaw for body-fixed rotation (z)
beta=90*np.pi/180 #Pitch for body-fixed rotation (y)
gamma=90*np.pi/180 #Roll for body-fixed rotation (x)

EulerRz=np.array([[np.cos(alpha),-np.sin(alpha),0],
             [np.sin(alpha),np.cos(alpha),0], 
             [0,0,1]])
EulerRy=np.array([[np.cos(beta),0,np.sin(beta)],
             [0,1,0],
             [-np.sin(beta),0,np.cos(beta)]])
EulerRx=np.array([[1,0,0],
             [0,np.cos(gamma),-np.sin(gamma)],
             [0,np.sin(gamma),np.cos(gamma)]])

V=np.array([[1,0,0]])
V=V.T
print("Column Vector V:")
print(V)

EulerRzyx=np.dot(np.dot(EulerRz,EulerRy),EulerRx)
EulerRzyxV=np.dot(EulerRzyx,V)

VOrigin=np.array([0,0,0,V[0],V[1],V[2]])
EulerRzyxVOrigin=np.array([0,0,0,EulerRzyxV[0],EulerRzyxV[1],EulerRzyxV[2]])

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(VOrigin[0],VOrigin[1],VOrigin[2],
          VOrigin[3],VOrigin[4],VOrigin[5],
          pivot='tail',normalize=False)
ax.quiver(EulerRzyxVOrigin[0],EulerRzyxVOrigin[1],EulerRzyxVOrigin[2],
          EulerRzyxVOrigin[3],EulerRzyxVOrigin[4],EulerRzyxVOrigin[5],
          pivot='tail',color='red',normalize=False)
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.set_zlim([-1, 1])

ax.set_xlabel('X,-z',size=14)
ax.set_ylabel('Y,-y', size=14)
ax.set_zlabel('Z,-x', size=14)
ax.set_title('Original Vector (Blue) + Euler ZYX')
ax.view_init(30,-115)
plt.savefig('ZYXBodyFixedRotations100.png',dpi=300,bbox_inches='tight')
print(VOrigin[0])

Original vector $<1,0,0>$ gone through body-fixed, Euler ZYX rotations of $90^{o}$ about each axis.

Additional Examples for Rotations

Additional Examples for Rotations

Properties

For any n-dimensional rotation matrix R acting on ℝⁿ,

• $R^{\mathrm {T} }=R^{-1}$ (The rotation is an orthogonal matrix)

It follows that:

• $\det R=\pm 1$

A rotation is termed proper if det R = 1, and improper (or a roto-reflection) if det R = –1.

Mathematical Examples

• The 2 × 2 rotation matrix

$Q={\begin{bmatrix}0&1\\-1&0\end{bmatrix}}$

corresponds to a 90° planar rotation clockwise about the origin.

• The transpose of the 2 × 2 matrix

$M={\begin{bmatrix}0.936&0.352\\0.352&-0.936\end{bmatrix}}$

is its inverse, but since its determinant is −1, this is not a proper rotation matrix; it is a reflection across the line 11y = 2x.

• The 3 × 3 rotation matrix

$Q={\begin{bmatrix}1&0&0\\0&{\frac {\sqrt {3}}{2}}&{\frac {1}{2}}\\0&-{\frac {1}{2}}&{\frac {\sqrt {3}}{2}}\end{bmatrix}}$

corresponds to a −30° rotation around the x-axis in three-dimensional space.

• The 3 × 3 rotation matrix

$Q={\begin{bmatrix}0.36&0.48&-0.8\\-0.8&0.60&0\\0.48&0.64&0.60\end{bmatrix}}$

corresponds to a rotation of approximately −74° around the axis (−1/3,2/3,2/3) in three-dimensional space.

• The 3 × 3 permutation matrix

$P={\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}}$

is a rotation matrix, as is the matrix of any even permutation, and rotates through 120° about the axis x = y = z.

• The 3 × 3 matrix

$M={\begin{bmatrix}3&-4&1\\5&3&-7\\-9&2&6\end{bmatrix}}$

has determinant +1, but is not orthogonal (its transpose is not its inverse), so it is not a rotation matrix.

• The 4 × 3 matrix

$M={\begin{bmatrix}0.5&-0.1&0.7\\0.1&0.5&-0.5\\-0.7&0.5&0.5\\-0.5&-0.7&-0.1\end{bmatrix}}$

is not square, and so cannot be a rotation matrix; yet M^TM yields a 3 × 3 identity matrix (the columns are orthonormal).

• The 4 × 4 matrix

$Q=-I={\begin{bmatrix}-1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{bmatrix}}$

describes an isoclinic rotation in four dimensions, a rotation through equal angles (180°) through two orthogonal planes.

• The 5 × 5 rotation matrix

$Q={\begin{bmatrix}0&-1&0&0&0\\1&0&0&0&0\\0&0&-1&0&0\\0&0&0&-1&0\\0&0&0&0&1\end{bmatrix}}$

rotates vectors in the plane of the first two coordinate axes 90°, rotates vectors in the plane of the next two axes 180°, and leaves the last coordinate axis unmoved.

Geometry

In Euclidean geometry, a rotation is an example of an isometry, a transformation that moves points without changing the distances between them. Rotations are distinguished from other isometries by two additional properties: they leave (at least) one point fixed, and they leave "handedness" unchanged. By contrast, a translation moves every point, a reflection exchanges left- and right-handed ordering, and a glide reflection does both.

A rotation that does not leave handedness unchanged is an improper rotation or a rotoinversion.

If a fixed point is taken as the origin of a Cartesian coordinate system, then every point can be given coordinates as a displacement from the origin. Thus one may work with the vector space of displacements instead of the points themselves. Now suppose (p₁,…,p_n) are the coordinates of the vector p from the origin O to point P. Choose an orthonormal basis for our coordinates; then the squared distance to P, by Pythagoras, is

$d^{2}(O,P)=\|\mathbf {p} \|^{2}=\sum _{r=1}^{n}p_{r}^{2}$

which can be computed using the matrix multiplication

$\|\mathbf {p} \|^{2}={\begin{bmatrix}p_{1}\cdots p_{n}\end{bmatrix}}{\begin{bmatrix}p_{1}\\\vdots \\p_{n}\end{bmatrix}}=\mathbf {p} ^{\mathrm {T} }\mathbf {p} .$

A geometric rotation transforms lines to lines, and preserves ratios of distances between points. From these properties it can be shown that a rotation is a linear transformation of the vectors, and thus can be written in matrix form, Qp. The fact that a rotation preserves, not just ratios, but distances themselves, is stated as

$\mathbf {p} ^{\mathrm {T} }\mathbf {p} =(Q\mathbf {p} )^{\mathrm {T} }(Q\mathbf {p} ),$

or

${\begin{aligned}\mathbf {p} ^{\mathrm {T} }I\mathbf {p} &{}=\left(\mathbf {p} ^{\mathrm {T} }Q^{\mathrm {T} }\right)(Q\mathbf {p} )\\&{}=\mathbf {p} ^{\mathrm {T} }\left(Q^{\mathrm {T} }Q\right)\mathbf {p} .\end{aligned}}$

Because this equation holds for all vectors, p, one concludes that every rotation matrix, Q, satisfies the orthogonality condition,

$Q^{\mathrm {T} }Q=I.$

Rotations preserve handedness because they cannot change the ordering of the axes, which implies the special matrix condition,

$\det Q=+1.$

Equally important, it can be shown that any matrix satisfying these two conditions acts as a rotation.

Multiplication

The inverse of a rotation matrix is its transpose, which is also a rotation matrix:

${\begin{aligned}\left(Q^{\mathrm {T} }\right)^{\mathrm {T} }\left(Q^{\mathrm {T} }\right)&=QQ^{\mathrm {T} }=I\\\det Q^{\mathrm {T} }&=\det Q=+1.\end{aligned}}$

The product of two rotation matrices is a rotation matrix:

${\begin{aligned}\left(Q_{1}Q_{2}\right)^{\mathrm {T} }\left(Q_{1}Q_{2}\right)&=Q_{2}^{\mathrm {T} }\left(Q_{1}^{\mathrm {T} }Q_{1}\right)Q_{2}=I\\\det \left(Q_{1}Q_{2}\right)&=\left(\det Q_{1}\right)\left(\det Q_{2}\right)=+1.\end{aligned}}$

For n > 2, multiplication of n × n rotation matrices is generally not commutative.

${\begin{aligned}Q_{1}&={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\end{bmatrix}}&Q_{2}&={\begin{bmatrix}0&0&1\\0&1&0\\-1&0&0\end{bmatrix}}\\Q_{1}Q_{2}&={\begin{bmatrix}0&-1&0\\0&0&1\\-1&0&0\end{bmatrix}}&Q_{2}Q_{1}&={\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}}.\end{aligned}}$

Noting that any identity matrix is a rotation matrix, and that matrix multiplication is associative, we may summarize all these properties by saying that the n × n rotation matrices form a group, which for n > 2 is non-abelian, called a special orthogonal group, and denoted by SO(n), SO(n,R), SO_n, or SO_n(R), the group of n × n rotation matrices is isomorphic to the group of rotations in an n-dimensional space. This means that multiplication of rotation matrices corresponds to composition of rotations, applied in left-to-right order of their corresponding matrices.

Robotic Position and Orientation (Copied and edited from Wikibooks)

In general, a rigid body in three-dimensional space has six degrees of freedom: three rotational and three translational.

The position and orientation of a rigid body can be described by attaching a frame to it.

A conventional way to describe the position and orientation of a rigid body is to attach a frame to it. After defining a reference coordinate system, the position and orientation of the rigid body are fully described by the position of the frame's origin and the orientation of its axes, relative to the reference frame.

Rotation Matrix

A rotation matrix describes the relative orientation of two such frames. The columns of this 3 × 3 matrix consist of the unit vectors along the axes of one frame, relative to the other, reference frame. Thus, the relative orientation of a frame $\{b\}$ with respect to a reference frame $\{a\}$ is given by the rotation matrix $_{a}^{b}R\,$:

$_{a}^{b}R={\begin{bmatrix}_{a}x^{b}&_{a}y^{b}&_{a}z^{b}\end{bmatrix}}={\begin{bmatrix}x^{b}\cdot x^{a}&y^{b}\cdot x^{a}&z^{b}\cdot x^{a}\\x^{b}\cdot y^{a}&y^{b}\cdot y^{a}&z^{b}\cdot y^{a}\\x^{b}\cdot z^{a}&y^{b}\cdot z^{a}&z^{b}\cdot z^{a}\end{bmatrix}}$

Rotation matrices can be interpreted in two ways:

1. As the representation of the rotation of the first frame into the second (active interpretation).
2. As the representation of the mutual orientation between two coordinate systems (passive interpretation).

The coordinates, relative to the reference frame $\{a\}$, of a point $p$, of which the coordinates are known with respect to a frame $\{b\}$ with the same origin, can then be calculated as follows: $_{a}p=\,_{a}^{b}R\,_{b}p$.

Representation of Reference Frame Using 3x3 Matrix of Direct Cosines (Dot Products)

Code

%reset -f
import numpy as np

alpha=45*np.pi/180 #Yaw for body-fixed rotation (z)
beta=45*np.pi/180 #Pitch for body-fixed rotation (y)
gamma=45*np.pi/180 #Roll for body-fixed rotation (x)

EulerRz=np.array([[np.cos(alpha),-np.sin(alpha),0],
             [np.sin(alpha),np.cos(alpha),0], 
             [0,0,1]])
EulerRy=np.array([[np.cos(beta),0,np.sin(beta)],
             [0,1,0],
             [-np.sin(beta),0,np.cos(beta)]])
EulerRx=np.array([[1,0,0],
             [0,np.cos(gamma),-np.sin(gamma)],
             [0,np.sin(gamma),np.cos(gamma)]])

EulerRzyx=np.dot(np.dot(EulerRz,EulerRy),EulerRx)
b_a_R=EulerRzyx
print('b_a_R or rotation matrix R for {b} respect to ref {a}')
print(np.round(b_a_R,2))

x_a=np.array([[1,0,0]])
x_a=x_a.T
y_a=np.array([[0,1,0]])
y_a=y_a.T
z_a=np.array([[0,0,1]])
z_a=z_a.T

x_b=np.dot(b_a_R,x_a)
y_b=np.dot(b_a_R,y_a)
z_b=np.dot(b_a_R,z_a)

b_a_R2=np.array([[np.vdot(x_b,x_a), np.vdot(y_b,x_a),np.vdot(z_b,x_a)],
                [np.vdot(x_b,y_a),np.vdot(y_b,y_a),np.vdot(z_b,y_a)],
                [np.vdot(x_b,z_a),np.vdot(y_b,z_a),np.vdot(z_b,z_a)]])

print('b_a_R or rotation matrix R for {b} respect to ref {a} using other definition')
print(np.round(b_a_R2,2))

print('Are the rotation matrices the same?')
print(b_a_R==b_a_R2)

Graphical Representation of Rotated Reference Frame about Origin

Reference reference frame A at origin

Rotated frame B at origin. Euler, body-fixed rotations (ZYX) each of 45 degrees.

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

alpha=45*np.pi/180 #Yaw for body-fixed rotation (z)
beta=45*np.pi/180 #Pitch for body-fixed rotation (y)
gamma=45*np.pi/180 #Roll for body-fixed rotation (x)

EulerRz=np.array([[np.cos(alpha),-np.sin(alpha),0],
             [np.sin(alpha),np.cos(alpha),0], 
             [0,0,1]])
EulerRy=np.array([[np.cos(beta),0,np.sin(beta)],
             [0,1,0],
             [-np.sin(beta),0,np.cos(beta)]])
EulerRx=np.array([[1,0,0],
             [0,np.cos(gamma),-np.sin(gamma)],
             [0,np.sin(gamma),np.cos(gamma)]])

EulerRzyx=np.dot(np.dot(EulerRz,EulerRy),EulerRx)
b_a_R=EulerRzyx

print('b_a_R or rotation matrix R for {b} respect to ref {a}')
print(np.round(b_a_R,2))

x_a=np.array([[1,0,0]])
x_a=x_a.T
y_a=np.array([[0,1,0]])
y_a=y_a.T
z_a=np.array([[0,0,1]])
z_a=z_a.T

x_b=np.dot(b_a_R,x_a)
y_b=np.dot(b_a_R,y_a)
z_b=np.dot(b_a_R,z_a)

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(0,0,0,x_a[0],x_a[1],x_a[2],pivot='tail',normalize=False,color='blue')
ax.quiver(0,0,0,y_a[0],y_a[1],y_a[2],pivot='tail',normalize=False,color='red')
ax.quiver(0,0,0,z_a[0],z_a[1],z_a[2],pivot='tail',normalize=False,color='green')
ax.text(x_a[0][0],x_a[1][0],x_a[2][0],'$x_a$',None,size=20)
ax.text(y_a[0][0],y_a[1][0],y_a[2][0],'$y_a$',None,size=20)
ax.text(z_a[0][0],z_a[1][0],z_a[2][0],'$z_a$',None,size=20)
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.set_zlim([-1, 1])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.xticks(np.linspace(-1,1,num=5))
plt.yticks(np.linspace(-1,1,num=5))
ax.set_zticks(np.linspace(-1,1,num=5))
ax.view_init(30,-115)
plt.savefig('ReferenceFrame_a_at_origin.png',dpi=300,bbox_inches='tight')

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(0,0,0,x_b[0],x_b[1],x_b[2],pivot='tail',normalize=False,color='blue')
ax.quiver(0,0,0,y_b[0],y_b[1],y_b[2],pivot='tail',normalize=False,color='red')
ax.quiver(0,0,0,z_b[0],z_b[1],z_b[2],pivot='tail',normalize=False,color='green')
ax.text(x_b[0][0],x_b[1][0],x_b[2][0],'$x_b$',None,size=20)
ax.text(y_b[0][0],y_b[1][0],y_b[2][0],'$y_b$',None,size=20)
ax.text(z_b[0][0],z_b[1][0],z_b[2][0],'$z_b$',None,size=20)
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.set_zlim([-1, 1])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.xticks(np.linspace(-1,1,num=5))
plt.yticks(np.linspace(-1,1,num=5))
ax.set_zticks(np.linspace(-1,1,num=5))
ax.view_init(30,-115)
plt.savefig('Rotated_frame_b_at_origin.png',dpi=300,bbox_inches='tight')

Graphical Representation of Point in Rotated Frame about Origin

If we have $_{a}p=<0.5,0.5,0.5>$ in reference frame $\{a\}$. What is $_{b}p$ in frame $\{b\}$ after Euler sequence ZYX by $45^{o}$ about each axis?

Point $p$ in reference frame $\{a\}$.

Point $p$ in rotated frame $\{b\}$.

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

alpha=45*np.pi/180 #Yaw for body-fixed rotation (z)
beta=45*np.pi/180 #Pitch for body-fixed rotation (y)
gamma=45*np.pi/180 #Roll for body-fixed rotation (x)

EulerRz=np.array([[np.cos(alpha),-np.sin(alpha),0],
             [np.sin(alpha),np.cos(alpha),0], 
             [0,0,1]])
EulerRy=np.array([[np.cos(beta),0,np.sin(beta)],
             [0,1,0],
             [-np.sin(beta),0,np.cos(beta)]])
EulerRx=np.array([[1,0,0],
             [0,np.cos(gamma),-np.sin(gamma)],
             [0,np.sin(gamma),np.cos(gamma)]])

EulerRzyx=np.dot(np.dot(EulerRz,EulerRy),EulerRx)

b_a_R=EulerRzyx
a_p=np.array([[0.5,0.5,0.5]])
a_p=a_p.T
a_b_R=b_a_R.T

#or

a_b_R=np.linalg.inv(b_a_R) #Simpler to use transpose, but...

b_p=np.dot(a_b_R,a_p)
print('The resulting b_p is')
print(np.round(b_p,2))

x_a=np.array([[1,0,0]])
x_a=x_a.T
y_a=np.array([[0,1,0]])
y_a=y_a.T
z_a=np.array([[0,0,1]])
z_a=z_a.T

x_b=np.dot(b_a_R,x_a)
y_b=np.dot(b_a_R,y_a)
z_b=np.dot(b_a_R,z_a)

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(0,0,0,x_a[0],x_a[1],x_a[2],pivot='tail',normalize=False,color='blue')
ax.quiver(0,0,0,y_a[0],y_a[1],y_a[2],pivot='tail',normalize=False,color='red')
ax.quiver(0,0,0,z_a[0],z_a[1],z_a[2],pivot='tail',normalize=False,color='green')
ax.text(x_a[0][0],x_a[1][0],x_a[2][0],'$x_a$',None,size=20)
ax.text(y_a[0][0],y_a[1][0],y_a[2][0],'$y_a$',None,size=20)
ax.text(z_a[0][0],z_a[1][0],z_a[2][0],'$z_a$',None,size=20)
ax.scatter(a_p[0],a_p[1],a_p[2],s=60,marker='x')
ax.text(a_p[0][0]+0.1,a_p[1][0],a_p[2][0],'$_a p$',None,size=20)
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.set_zlim([-1, 1])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.xticks(np.linspace(-1,1,num=5))
plt.yticks(np.linspace(-1,1,num=5))
ax.set_zticks(np.linspace(-1,1,num=5))
ax.view_init(30,-115)
plt.savefig('Ref_a_with_point.png',dpi=300,bbox_inches='tight')

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(0,0,0,x_b[0],x_b[1],x_b[2],pivot='tail',normalize=False,color='blue')
ax.quiver(0,0,0,y_b[0],y_b[1],y_b[2],pivot='tail',normalize=False,color='red')
ax.quiver(0,0,0,z_b[0],z_b[1],z_b[2],pivot='tail',normalize=False,color='green')
ax.text(x_b[0][0],x_b[1][0],x_b[2][0],'$x_b$',None,size=20)
ax.text(y_b[0][0],y_b[1][0],y_b[2][0],'$y_b$',None,size=20)
ax.text(z_b[0][0],z_b[1][0],z_b[2][0],'$z_b$',None,size=20)
ax.scatter(a_p[0],a_p[1],a_p[2],s=60,marker='x')
ax.text(a_p[0][0]+0.1,a_p[1][0],a_p[2][0],'$_b p$',None,size=20)
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.set_zlim([-1, 1])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.xticks(np.linspace(-1,1,num=5))
plt.yticks(np.linspace(-1,1,num=5))
ax.set_zticks(np.linspace(-1,1,num=5))
ax.view_init(30,-115)
plt.savefig('Rotated_Frame_b_with_point_at_origin.png',dpi=300,bbox_inches='tight')

Additional Examples for Rotations and Coordinates

Additional Examples for Rotations and Coordinates

Properties

Some of the properties of the rotation matrix that may be of practical value, are:

1. The column vectors of $_{a}^{b}R\,$ are normal to each other.
2. The length of the column vectors of $_{a}^{b}R\,$ equals 1.
3. A rotation matrix is a non-minimal description of a rigid body's orientation. That is, it uses nine numbers to represent an orientation instead of just three. (The two above properties correspond to six relations between the nine matrix elements. Hence, only three of them are independent.) Non-minimal representations often have some numerical advantages, though, as they do not exhibit coordinate singularities.
4. Since $_{a}^{b}R\,$ is orthonormal, $_{b}^{a}R=\,_{a}^{b}R^{-1}=\,_{a}^{b}R^{T}$.

Elementary Rotations about Frame Axes

Rotation by an angle $\gamma$ about the z-axis.

The expressions for elementary rotations about frame axes can easily be derived. From the figure on the right, it can be seen that the rotation of a frame by an angle $\gamma$ about the z-axis, is described by:

$R_{z}(\gamma )={\begin{bmatrix}\cos(\gamma )&-\sin(\gamma )&0\\\sin(\gamma )&\cos(\gamma )&0\\0&0&1\end{bmatrix}}$

Similarly, it can be shown that the rotation of a frame by an angle $\alpha$ about the x-axis, is given by:

$R_{x}(\alpha )={\begin{bmatrix}1&0&0\\0&\cos(\alpha )&-\sin(\alpha )\\0&\sin(\alpha )&\cos(\alpha )\end{bmatrix}}$

Derived in exactly the same manner, the rotation of a frame by an angle $\beta$ about the y-axis, is described by:

$R_{y}(\beta )={\begin{bmatrix}\cos(\beta )&0&\sin(\beta )\\0&1&0\\-\sin(\beta )&0&\cos(\beta )\end{bmatrix}}$

Compound Rotations

Compound rotations are found by multiplication of the different elementary rotation matrices.

The matrix corresponding to a set of rotations about moving axes can be found by postmultiplying the rotation matrices, thus multiplying them in the same order in which the rotations take place. The rotation matrix formed by a rotation by an angle $\alpha$ about the z-axis followed by a rotation by an angle $-\beta$ about the moved y-axis, is then given by:

$R(zy,\alpha ,-\beta )=R(z,\alpha )R(y,-\beta )$

The composition of rotations about fixed axes, on the other hand, is found by premultiplying the different elementary rotation matrices.

Inverse Rotations

The inverse of a single rotation about a frame axis is a rotation by the negative of the rotation angle about the same axis:

$R^{-1}(z,\alpha )=R(z,-\alpha )$

The inverse of a compound rotation follows from the inverse of the matrix product:

$R^{-1}(zy,\alpha ,-\beta )=R^{-1}(y,-\beta )R^{-1}(z,\alpha )$

Euler Angles

Contrary to the rotation matrix, Euler angles are a minimal representation (a set of just three numbers, that is) of relative orientation. This set of three angles describes a sequence of rotations about the axes of a moving reference frame. There are, however, many (12, to be exact) sets that describe the same orientation: different combinations of axes (e.g. ZXZ, ZYZ, and so on) lead to different Euler angles. Euler angles are often used for the description of the orientation of the wrist-like end-effectors of many serial manipulator robots.

Note: Identical axes should not be in consecutive places (e.g. ZZX). Also, the range of the Euler angles should be limited in order to avoid different angles for the same orientation. E.g.: for the case of ZYZ Euler angles, the first rotation about the z-axis should be within $[-\pi ,\pi ]$. The second rotation, about the moved y-axis, has a range of $[-\pi /2,\pi /2]$. The last rotation, about the moved z-axis, has a range of $[-\pi ,\pi ]$.

Forward Mapping

Forward mapping, or finding the orientation of the end-effector with respect to the base frame, follows from the composition of rotations about moving axes. For a rotation by an angle $\alpha$ about the z-axis, followed by a rotation by an angle $\beta$ about the moved x-axis, and a final rotation by an angle $\gamma$ about the moved z-axis, the resulting rotation matrix is:

$_{bs}^{ee}R\,=R(zxz,\alpha ,\beta ,\gamma )=R(z,\alpha )R(x,\beta )R(z,\gamma )$

After writing out:

$R(zxz,\alpha ,\beta ,\gamma )={\begin{bmatrix}c_{\gamma }c_{\alpha }-s_{\gamma }c_{\beta }s_{\alpha }&-s_{\gamma }c_{\alpha }-c_{\gamma }c_{\beta }s_{\alpha }&s_{\beta }s_{\alpha }\\c_{\gamma }s_{\alpha }+s_{\gamma }c_{\beta }c_{\alpha }&-s_{\gamma }s_{\alpha }+c_{\gamma }c_{\beta }c_{\alpha }&-s_{\beta }c_{\alpha }\\s_{\gamma }s_{\beta }&c_{\gamma }s_{\beta }&c_{\beta }\end{bmatrix}}$

Note: Notice the shorthand notation: $s_{\alpha }$ stands for $\sin \alpha$, $c_{\alpha }$ stands for $\cos \alpha$, and so on.

Inverse Mapping

In order to drive the end-effector, the inverse problem must be solved: given a certain orientation matrix, which are the Euler angles that accomplish this orientation?

For the above case, the Euler angles $\alpha$, $\beta$ and $\gamma$ are found by inspection of the rotation matrix:

$\alpha ={\textrm {atan2}}(R_{13},-R_{23})$

$\beta ={\textrm {atan2}}(-R_{23}c_{\alpha }+R_{13}s_{\alpha },R_{33})$

$\gamma ={\textrm {atan2}}(R_{31},R_{32})$

Example of Forward Mapping and Inverse Mapping by Inspection

Code

%reset -f
import numpy as np
import sympy as sp

alpha, beta, gamma = sp.symbols('alpha beta gamma')

EulerRz_alpha=np.array([[sp.cos(alpha),-sp.sin(alpha),0],
             [sp.sin(alpha),sp.cos(alpha),0], 
             [0,0,1]])
EulerRx_beta=np.array([[1,0,0],
             [0,sp.cos(beta),-sp.sin(beta)],
             [0,sp.sin(beta),sp.cos(beta)]])
EulerRz_gamma=np.array([[sp.cos(gamma),-sp.sin(gamma),0],
             [sp.sin(gamma),sp.cos(gamma),0], 
             [0,0,1]])

Rzxz=np.dot(np.dot(EulerRz_alpha,EulerRx_beta),
                           EulerRz_gamma)
print("Rzxz:")
print(Rzxz)

alpha_inspected=sp.atan(Rzxz[0,2]/-(Rzxz[1,2]))
alpha_inspected=sp.simplify(alpha_inspected)
print("alpha:")
print(alpha_inspected)

beta_inspected=sp.atan((-Rzxz[1][2]*sp.cos(alpha)+
                       Rzxz[0][2]*sp.sin(alpha))/Rzxz[2][2])
beta_inspected=sp.simplify(beta_inspected)
print("beta:")
print(beta_inspected)

gamma_inspected=sp.atan(Rzxz[2][0]/Rzxz[2][1])
gamma_inspected=sp.simplify(gamma_inspected)
print("gamma:")
print(gamma_inspected)

Coordinate Singularities

In the above example, a coordinate singularity exists for $\beta =0$. The above equations are badly numerically conditioned for small values of $\beta$: the first and last equaton become undefined. This corresponds with an alignment of the first and last axes of the end-effector. The occurrence of a coordinate singularity involves the loss of a degree of freedom: in the case of the above example, small rotations about the y-axis require impossibly large rotations about the x- and z-axes.

No minimal representation of orientation can globally describe all orientations without coordinate singularities occurring.

Roll-Pitch-Yaw Angles

The orientation of a rigid body can equally well be described by three consecutive rotations about fixed axes. This leads to a notation with Roll-Pitch-Yaw (RPY) angles.

Forward Mapping

The forward mapping of RPY angles to a rotation matrix similar to that of Euler angles. Since the frame now rotates about fixed axes instead of moving axes, the order in which the different rotation matrices are multiplied is inversed:

$R(RPY,r,p,y)=R(z,y)R(y,p)R(x,r)$

After writing out:

$R(RPY,r,p,y)={\begin{bmatrix}c_{y}c_{p}&c_{y}s_{p}s_{r}-s_{y}c_{r}&c_{y}s_{p}c_{r}+s_{y}s_{r}\\s_{y}c_{p}&s_{y}s_{p}s_{r}+c_{y}c_{r}&s_{y}s_{p}c_{r}-c_{y}s_{r}\\-s_{p}&c_{p}s_{r}&c_{p}c_{r}\end{bmatrix}}$

Inverse Mapping

The inverse relationships are found from inspection of the rotation matrix above:

$r={\textrm {atan2}}(R_{32},R_{33})$

$y={\textrm {atan2}}(R_{21},R_{11})$

$p={\textrm {atan2}}(-R_{31},c_{y}R_{11}+s_{y}R_{21})$

Note: The above equations are badly numerically conditioned for values of $p$ near $\pi /2$ and $-\pi /2$.

Unit Quaternions

Unit quaternions (quaternions of which the absolute value equals 1) are another representation of orientation. They can be seen as a compromise between the advantages and disadvantages of rotation matrices and Euler angle sets.

Homogeneous Transform

The notations above describe only relative orientation. The coordinates of a point $_{a}p$ with $_{b}p$ relative to a frame $\{b\}$, rotated and translated with respect to a reference frame $\{a\}$, are given by:

$_{a}p=\,_{a}^{b}R\,_{b}p+_{a}p^{a,b}$

This can be compacted into the form of a homogeneous transformation matrix or pose (matrix). It is defined as follows:

$_{a}^{b}T={\begin{bmatrix}^{b}_{a}R&_{a}p^{a,b}\\0_{1\times 3}&1\end{bmatrix}}$

This matrix represents the position and orientation of a frame $\{b\}$ whose origin, relative to a reference frame $\{a\}$, is described by $_{a}p^{a,b}$, and whose orientation, relative to the same reference frame $\{a\}$, is described by the rotation matrix $_{a}^{b}R\,$.

$_{a}^{b}T\,$ is, thus, the representation of a frame in three-dimensional space. If the coordinates of a point $p$ are known with respect to a frame $\{b\}$, then its coordinates, relative to $\{a\}$ are found by:

${\begin{bmatrix}_{a}p\\1\end{bmatrix}}=\,_{a}^{b}T{\begin{bmatrix}_{b}p\\1\end{bmatrix}}$

This is the same as writing:

$_{a}p=\,_{a}^{b}R\,_{b}p+_{a}p^{a,b}$

Note that the above vectors are extended with a fourth coordinate equal to one: they're made homogeneous.

As was the case with rotation matrices, homogeneous transformation matrices can be interpreted in an active ("displacement"), and a passive ("pose") manner. It is also a non-minimal representation of a pose, that does not suffer from coordinate singularities.

Graphical Representation of Point in Rotated and Translated Frame (Not Using T)

Point $p$ in rotated and translated frame $\{b\}$.

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

a_p=np.array([[1,1,1]])
a_p=a_p.T

a_p_ab=np.array([[0.8, 0.8, 0.8]])
a_p_ab=a_p_ab.T

alpha=45*np.pi/180 #Yaw for body-fixed rotation (z)
beta=45*np.pi/180 #Pitch for body-fixed rotation (y)
gamma=45*np.pi/180 #Roll for body-fixed rotation (x)

EulerRz=np.array([[np.cos(alpha),-np.sin(alpha),0],
             [np.sin(alpha),np.cos(alpha),0], 
             [0,0,1]])
EulerRy=np.array([[np.cos(beta),0,np.sin(beta)],
             [0,1,0],
             [-np.sin(beta),0,np.cos(beta)]])
EulerRx=np.array([[1,0,0],
             [0,np.cos(gamma),-np.sin(gamma)],
             [0,np.sin(gamma),np.cos(gamma)]])

EulerRzyx=np.dot(np.dot(EulerRz,EulerRy),EulerRx)

b_a_R=EulerRzyx
a_b_R=b_a_R.T


b_p=np.dot(a_b_R,a_p-a_p_ab)

print('The resulting b_p is')
print(np.round(b_p,2))

x_a=np.array([[1,0,0]])
x_a=x_a.T
y_a=np.array([[0,1,0]])
y_a=y_a.T
z_a=np.array([[0,0,1]])
z_a=z_a.T

x_b=np.dot(b_a_R,x_a)
y_b=np.dot(b_a_R,y_a)
z_b=np.dot(b_a_R,z_a)

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(0,0,0,x_a[0],x_a[1],x_a[2],pivot='tail',normalize=False,color='blue')
ax.quiver(0,0,0,y_a[0],y_a[1],y_a[2],pivot='tail',normalize=False,color='red')
ax.quiver(0,0,0,z_a[0],z_a[1],z_a[2],pivot='tail',normalize=False,color='green')
ax.text(x_a[0][0],x_a[1][0],x_a[2][0],'$x_a$',None,size=20)
ax.text(y_a[0][0],y_a[1][0],y_a[2][0],'$y_a$',None,size=20)
ax.text(z_a[0][0],z_a[1][0],z_a[2][0],'$z_a$',None,size=20)
ax.scatter(a_p[0],a_p[1],a_p[2],s=60,marker='x')
ax.text(a_p[0][0]+0.1,a_p[1][0],a_p[2][0],'$_a p$',None,size=20)

#fig=plt.figure()
#ax=fig.add_subplot(111,projection='3d')
ax.quiver(a_p_ab[0],a_p_ab[1],a_p_ab[2],
          x_b[0],x_b[1],x_b[2],pivot='tail',normalize=False,color='blue')
ax.quiver(a_p_ab[0],a_p_ab[1],a_p_ab[2],
          y_b[0],y_b[1],y_b[2],pivot='tail',normalize=False,color='red')
ax.quiver(a_p_ab[0],a_p_ab[1],a_p_ab[2],
          z_b[0],z_b[1],z_b[2],pivot='tail',normalize=False,color='green')
ax.text(a_p_ab[0][0]+x_b[0][0],a_p_ab[1][0]+x_b[1][0],
        a_p_ab[2][0]+x_b[2][0],'$x_b$',None,size=20)
ax.text(a_p_ab[0][0]+y_b[0][0],a_p_ab[1][0]+y_b[1][0],
        a_p_ab[2][0]+y_b[2][0],'$y_b$',None,size=20)
ax.text(a_p_ab[0][0]+z_b[0][0],a_p_ab[1][0]+z_b[1][0],
        a_p_ab[2][0]+z_b[2][0],'$z_b$',None,size=20)
ax.scatter(a_p[0],a_p[1],a_p[2],s=60,marker='x')
ax.set_xlim([-0.5, 1.5])
ax.set_ylim([-0.5, 1.5])
ax.set_zlim([-0.5, 1.5])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.xticks(np.linspace(-0.5,1.5,num=5))
plt.yticks(np.linspace(-0.5,1.5,num=5))
ax.set_zticks(np.linspace(-0.5,1.5,num=5))
ax.view_init(30,-115)
plt.savefig('a_P_Frameb_translation_rotation.png',dpi=300,bbox_inches='tight')

Representation of Point in Rotated and Translated Frame (Using T)

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

a_p=np.array([[1,1,1]])
a_p=a_p.T

a_p_ab=np.array([[0.8, 0.8, 0.8]])
a_p_ab=a_p_ab.T

alpha=45*np.pi/180 #Yaw for body-fixed rotation (z)
beta=45*np.pi/180 #Pitch for body-fixed rotation (y)
gamma=45*np.pi/180 #Roll for body-fixed rotation (x)

EulerRz=np.array([[np.cos(alpha),-np.sin(alpha),0],
             [np.sin(alpha),np.cos(alpha),0], 
             [0,0,1]])
EulerRy=np.array([[np.cos(beta),0,np.sin(beta)],
             [0,1,0],
             [-np.sin(beta),0,np.cos(beta)]])
EulerRx=np.array([[1,0,0],
             [0,np.cos(gamma),-np.sin(gamma)],
             [0,np.sin(gamma),np.cos(gamma)]])

EulerRzyx=np.dot(np.dot(EulerRz,EulerRy),EulerRx)

b_a_R=EulerRzyx

print("b_a_R (Rotation of frame b with respect to frame a):")
print(np.round(b_a_R,2))
print("a_p_ab (Translation of frame b from frame a in frame a):")
print(np.round(a_p_ab,2))

b_a_T=np.append(b_a_R,np.zeros([1,3]),axis=0)
b_a_T=np.append(b_a_T,np.append(a_p_ab,[[1]],axis=0),axis=1)

print("Homogeneous Transform b_a_T:")
print(np.round(b_a_T,2))


a_b_T=np.linalg.inv(b_a_T)
# or
a_b_T=np.append(b_a_R.T,np.zeros([1,3]),axis=0)
a_b_T=np.append(a_b_T,np.append(-np.dot(b_a_R.T,a_p_ab),
                                [[1]],axis=0),axis=1)

print("Inverse of b_a_T or a_b_T:")
print(np.round(a_b_T,2))

a_p_1=np.append(a_p,[[1]],axis=0)
b_p_1=np.dot(a_b_T,a_p_1)
b_p=np.delete(b_p_1,3,axis=0)

print("Resulting b_p")
print(np.round(b_p,2))

Compound Poses

If the pose of a frame $\{c\}$ is known, relative to $\{b\}$, whose pose is known with respect to a third frame $\{a\}$, the resulting pose $_{a}^{c}T\,$ is found as follows:

$_{a}^{c}T=\,_{a}^{b}T\,_{b}^{c}T$

Graphical Representation of Compound Poses

If we know the transformation $_{a}^{b}T$ from frame $\{b\}$ relative to reference frame $\{a\}$ and the transformation $_{b}^{c}T$ from frame $\{c\}$ to $\{b\}$, we can describe the transformation from $_{a}^{c}T$ from frame $\{c\}$ to reference frame $\{a\}$.

$_{a}^{c}T=\,_{a}^{b}T\,_{b}^{c}T$

Plotted frames for compound poses going from reference frame $\{a\}$ to $\{b\}$ to $\{c\}$.

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

a_p_ab=np.array([[0.8, 0.8, 0.8]])
a_p_ab=a_p_ab.T

alpha=45*np.pi/180 #Yaw for body-fixed rotation (z)
beta=45*np.pi/180 #Pitch for body-fixed rotation (y)
gamma=45*np.pi/180 #Roll for body-fixed rotation (x)

EulerRz=np.array([[np.cos(alpha),-np.sin(alpha),0],
             [np.sin(alpha),np.cos(alpha),0], 
             [0,0,1]])
EulerRy=np.array([[np.cos(beta),0,np.sin(beta)],
             [0,1,0],
             [-np.sin(beta),0,np.cos(beta)]])
EulerRx=np.array([[1,0,0],
             [0,np.cos(gamma),-np.sin(gamma)],
             [0,np.sin(gamma),np.cos(gamma)]])

EulerRzyx=np.dot(np.dot(EulerRz,EulerRy),EulerRx)

b_a_R=EulerRzyx

b_a_T=np.append(b_a_R,np.zeros([1,3]),axis=0)
b_a_T=np.append(b_a_T,np.append(a_p_ab,[[1]],axis=0),axis=1)

print("Homogeneous Transform b_a_T:")
print(np.round(b_a_T,2))

c_b_T=b_a_T;

print("Homogeneous Transform c_b_T:")
print(np.round(c_b_T,2))

c_a_T=np.dot(b_a_T,c_b_T)

print("Homogeneous Transform c_a_T:")
print(np.round(c_a_T,2))

x_a=np.array([[1,0,0]])
x_a=x_a.T
y_a=np.array([[0,1,0]])
y_a=y_a.T
z_a=np.array([[0,0,1]])
z_a=z_a.T

#Extract rotation matrix from homogeneous transform
b_a_R=np.delete(b_a_T,3,axis=0);
b_a_R=np.delete(b_a_R,3,axis=1);

#Extract translation from homogenous transform
a_p_ab=np.array([[b_a_T[0][3]],[b_a_T[1][3]],[b_a_T[2][3]]])

#Calculate coordinate axes for {b} in {a}
x_b=np.dot(b_a_R,x_a)
y_b=np.dot(b_a_R,y_a)
z_b=np.dot(b_a_R,z_a)

#Extract rotation matrix from homogeneous transform
c_a_R=np.delete(c_a_T,3,axis=0);
c_a_R=np.delete(c_a_R,3,axis=1);

#Extract translation from homogeneous transform
a_p_ac=np.array([[c_a_T[0][3]],[c_a_T[1][3]],[c_a_T[2][3]]])

#Calculate coordinate axes for {c} in {a}
x_c=np.dot(c_a_R,x_a)
y_c=np.dot(c_a_R,y_a)
z_c=np.dot(c_a_R,z_a)

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.quiver(0,0,0,x_a[0],x_a[1],x_a[2],pivot='tail',normalize=False,color='blue')
ax.quiver(0,0,0,y_a[0],y_a[1],y_a[2],pivot='tail',normalize=False,color='red')
ax.quiver(0,0,0,z_a[0],z_a[1],z_a[2],pivot='tail',normalize=False,color='green')
ax.text(x_a[0][0],x_a[1][0],x_a[2][0],'$x_a$',None,size=20)
ax.text(y_a[0][0],y_a[1][0],y_a[2][0],'$y_a$',None,size=20)
ax.text(z_a[0][0],z_a[1][0],z_a[2][0],'$z_a$',None,size=20)

#fig=plt.figure()
#ax=fig.add_subplot(111,projection='3d')
ax.quiver(a_p_ab[0],a_p_ab[1],a_p_ab[2],
          x_b[0],x_b[1],x_b[2],pivot='tail',normalize=False,color='blue')
ax.quiver(a_p_ab[0],a_p_ab[1],a_p_ab[2],
          y_b[0],y_b[1],y_b[2],pivot='tail',normalize=False,color='red')
ax.quiver(a_p_ab[0],a_p_ab[1],a_p_ab[2],
          z_b[0],z_b[1],z_b[2],pivot='tail',normalize=False,color='green')
ax.text(a_p_ab[0][0]+x_b[0][0],a_p_ab[1][0]+x_b[1][0],
        a_p_ab[2][0]+x_b[2][0],'$x_b$',None,size=20)
ax.text(a_p_ab[0][0]+y_b[0][0],a_p_ab[1][0]+y_b[1][0],
        a_p_ab[2][0]+y_b[2][0],'$y_b$',None,size=20)
ax.text(a_p_ab[0][0]+z_b[0][0],a_p_ab[1][0]+z_b[1][0],
        a_p_ab[2][0]+z_b[2][0],'$z_b$',None,size=20)

#fig=plt.figure()
#ax=fig.add_subplot(111,projection='3d')
ax.quiver(a_p_ac[0],a_p_ac[1],a_p_ac[2],
          x_c[0],x_c[1],x_c[2],pivot='tail',normalize=False,color='blue')
ax.quiver(a_p_ac[0],a_p_ac[1],a_p_ac[2],
          y_c[0],y_c[1],y_c[2],pivot='tail',normalize=False,color='red')
ax.quiver(a_p_ac[0],a_p_ac[1],a_p_ac[2],
          z_c[0],z_c[1],z_c[2],pivot='tail',normalize=False,color='green')
ax.text(a_p_ac[0][0]+x_c[0][0],a_p_ac[1][0]+x_c[1][0],
        a_p_ac[2][0]+x_c[2][0],'$x_c$',None,size=20)
ax.text(a_p_ac[0][0]+y_c[0][0],a_p_ac[1][0]+y_c[1][0],
        a_p_ac[2][0]+y_c[2][0],'$y_c$',None,size=20)
ax.text(a_p_ac[0][0]+z_c[0][0],a_p_ac[1][0]+z_c[1][0],
        a_p_ac[2][0]+z_c[2][0],'$z_c$',None,size=20)

ax.set_xlim([0, 2])
ax.set_ylim([0, 2])
ax.set_zlim([0, 2])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.xticks(np.linspace(0,2,num=5))
plt.yticks(np.linspace(0,2,num=5))
ax.set_zticks(np.linspace(0,2,num=5))
ax.view_init(30,-115)
plt.savefig('CompoundPoses_c_b_a.png',dpi=300,bbox_inches='tight')

Additional Examples of Homogeneous Transforms

Additional Examples of Homogeneous Transforms

Finite Displacement Twist

A pose matrix is a non-minimal way of describing a pose. A frequently used minimal alternative is the finite displacement twist:

$t={\begin{bmatrix}\alpha \\\beta \\\gamma \\x\\y\\z\end{bmatrix}}$

Here, $\alpha$, $\beta$ and $\gamma$ are a valid set (any) of Euler angles, while $x$, $y$ and $z$ are the coordinates of a reference point on the rigid body.

Forward Kinematics (Copied and Edited from Link and Link)

An articulated six DOF robotic arm uses forward kinematics to position the gripper.

The forward kinematics equations define the trajectory of the end-effector of a PUMA robot reaching for parts.

Forward kinematics refers to the use of the kinematic equations of a robot to compute the position of the end effector from specified values for the joint parameters.

The kinematics equations of the robot are used in robotics, computer games, and animation. The reverse process that computes the joint parameters that achieve a specified position of the end effector is known as inverse kinematics.

Forward vs Backwards Kinematics

Forward Position Kinematics

The forward position kinematics problem is: given the different joint angles, what is the position of the end-effector? With the previous sections in mind, the answer is: construct the different transformation matrices and combine them in the right way, the result being $_{bs}^{ee}T\,$, where $\{bs\}$ is the base frame of the robot manipulator.

Solution

Suppose the mutual orientation matrices between adjacent links are known. (As the fixed parameters of each link are known, and the joint angles are a given to the problem, these can be calculated. One possible way to do this would be to make use of the Denavit-Hartenberg convention.) The transformation that relates the last and first frames in a serial manipulator arm, and thus, the solution to the forward kinematics problem, is then represented by the compound homogeneous transformation matrix. The axes are moving, thus, the compound homogeneous transformation matrix is found by multiplying the individual transformation matrices:

$_{bs}^{ee}T=\,_{0}^{N}T=\,_{0}^{1}T\,_{1}^{2}T\ldots \,_{N-2}^{N-1}T\,_{N-1}^{N}T$

Examples

The Planar Three-Link Manipulator

A planar three link manipulator. Each $X_{i}$-axis lies along the $i$th link. Each $Y_{i}$-axis lies perpendicular to the corresponding $X_{i}$-axis in such a way that a positive $\theta _{i}$ corresponds with a rotation from $X_{i}$ to $Y_{i}$.

The equations below use 3 × 3 pose matrices (homogeneous transformations), as this is just a 2-dimensional case (cf. the figure on the right).

The pose of the first link, relative to the reference frame, is given by (recall the elementary rotation about the z-axis from the previous section):

$T_{1}(\theta _{1})={\begin{bmatrix}\cos(\theta _{1})&-\sin(\theta _{1})&0\\\sin(\theta _{1})&\cos(\theta _{1})&0\\0&0&1\end{bmatrix}}$

The pose of the second link, relative to the first link, is given by:

$T_{2}(\theta _{2})={\begin{bmatrix}\cos(\theta _{2})&-\sin(\theta _{2})&l_{1}\\\sin(\theta _{2})&\cos(\theta _{2})&0\\0&0&1\end{bmatrix}}$

This corresponds to a rotation by an angle $\theta _{2}$ and a translation by a distance $l_{1}$, where $l_{1}$ is the length of the first link.

The pose of the third link, relative to the second link, is given by:

$T_{3}(\theta _{3})={\begin{bmatrix}\cos(\theta _{3})&-\sin(\theta _{3})&l_{2}\\\sin(\theta _{3})&\cos(\theta _{3})&0\\0&0&1\end{bmatrix}}$

The pose of the end effector, relative to the third link, is given by:

$T_{4}={\begin{bmatrix}1&0&l_{3}\\0&1&0\\0&0&1\end{bmatrix}}$

The solution to the forward kinematics problem is then:

$_{bs}^{ee}T=\,_{0}^{4}T(\theta _{1},\theta _{2},\theta _{3})={\begin{bmatrix}c_{123}&-s_{123}&l_{1}c_{1}+l_{2}c_{12}+l_{3}c_{123}\\s_{123}&c_{123}&l_{1}s_{1}+l_{2}s_{12}+l_{3}s_{123}\\0&0&1\end{bmatrix}}$

Hence:

${\begin{bmatrix}x\\y\\1\end{bmatrix}}=T{\begin{bmatrix}0\\0\\1\end{bmatrix}}$

The resulting kinematic equations are:

${\begin{array}{l}x=l_{1}\cos \theta _{1}+l_{2}\cos(\theta _{1}+\theta _{2})+l_{3}\cos(\theta _{1}+\theta _{2}+\theta _{3})\\y=l_{1}\sin \theta _{1}+l_{2}\sin(\theta _{1}+\theta _{2})+l_{3}\sin(\theta _{1}+\theta _{2}+\theta _{3})\end{array}}$

Graphical Example of Planar, Three-link Manipulator using Compound Transformations

Planar, three-link manipulator with all three angles set to $30^{o}$.

Code

%reset -f
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt

theta1, theta2, theta3=sp.symbols('theta1 theta2 theta3')
l1, l2, l3 = sp.symbols('l1 l2 l3')

f1_f0_T=np.array([[sp.cos(theta1), -sp.sin(theta1), 0],
             [sp.sin(theta1), sp.cos(theta1), 0],
             [0, 0, 1]])
f2_f1_T=np.array([[sp.cos(theta2), -sp.sin(theta2), l1],
            [sp.sin(theta2), sp.cos(theta2),0],
            [0, 0, 1]])
f3_f2_T=np.array([[sp.cos(theta3), -sp.sin(theta3), l2],
            [sp.sin(theta3), sp.cos(theta3),0],
            [0, 0, 1]])
f4_f3_T=np.array([[sp.cos(0), -sp.sin(0), l3],
            [sp.sin(0), sp.cos(0),0],
            [0, 0, 1]])
ee_bs_T=np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,f4_f3_T)))
ee_bs_T=sp.simplify(ee_bs_T) # Unfortunately, we do not get the simple
# expression on the wiki.
#print("ee_bs_T")
#display(ee_bs_T)

#For substituting in the following: 30 degree increments
#print("ee_bs_T after substitutions")
replacements=[(theta1,30*np.pi/180),(theta2,30*np.pi/180), 
              (theta3,30*np.pi/180), (l1,1), (l2,1), (l3,1)]

#display(ee_bs_T.subs(replacements))

End_Coord=np.array([[0,0,1]])
End_Coord=End_Coord.T

#print("f1_f0_T")
f1_f0_T=sp.simplify(f1_f0_T)
#display(f1_f0_T.subs(replacements))
f1_f0_T=np.array(f1_f0_T.subs(replacements)).astype(np.float64)
f1_f0_T=np.reshape(f1_f0_T,(3,3))
print("f1_f0_T dot End_Coord")
display(np.dot(f1_f0_T,End_Coord))
Joint0=np.dot(f1_f0_T,End_Coord)

#print("\nf2_f1_T")
f2_f1_T=sp.simplify(f2_f1_T)
#display(f2_f1_T.subs(replacements))
f2_f1_T=np.array(f2_f1_T.subs(replacements)).astype(np.float64)
f2_f1_T=np.reshape(f2_f1_T,(3,3))
print("f2_f0_T dot End_Coord")
display(np.dot(f1_f0_T,np.dot(f2_f1_T,End_Coord)))
Joint1=np.dot(f1_f0_T,np.dot(f2_f1_T,End_Coord))

#print("\nf3_f2_T")
f3_f2_T=sp.simplify(f3_f2_T)
#display(f3_f2_T.subs(replacements))
f3_f2_T=np.array(f3_f2_T.subs(replacements)).astype(np.float64)
f3_f2_T=np.reshape(f3_f2_T,(3,3))
print("f3_f0_T dot End_Coord")
display(np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,End_Coord))))
Joint2=np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,End_Coord)))

#print("\nf4_f3_T")
f4_f3_T=sp.simplify(f4_f3_T)
#display(f4_f3_T.subs(replacements))
f4_f3_T=np.array(f4_f3_T.subs(replacements)).astype(np.float64)
f4_f3_T=np.reshape(f4_f3_T,(3,3))
print("f4_f0_T dot End_Coord")
display(np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,np.dot(f4_f3_T,End_Coord)))))
EndEffector=np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,np.dot(f4_f3_T,End_Coord))))

fig=plt.figure()
ax=fig.add_subplot(111)
plt.plot([Joint0[0][0], Joint1[0][0]],[Joint0[1][0],Joint1[1][0]],'bo-')
plt.plot([Joint1[0][0], Joint2[0][0]],[Joint1[1][0],Joint2[1][0]],'ro-')
plt.plot([Joint2[0][0], EndEffector[0][0]],
         [Joint2[1][0],EndEffector[1][0]],'go-')

ax.set_xlim([0, 1])
plt.axis('equal')
ax.set_xlabel('X',size=20)
ax.set_ylabel('Y',size=20)
plt.savefig('2D_30_30_30_rotations_200212.png', dpi=300, bbox_inches='tight')

Two Configurations for the Same Resulting Location of the End Effector

An example of two different solutions for the inverse kinematics problem leading to the same end-effector position and orientation.

We can demonstrate how to have the same position of an end effector with two different configurations of the planar serial manipulator.

Example for a Different Configuration for the Same Resulting Location of the End Effector

Code

%reset -f
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt

theta1, theta2, theta3=sp.symbols('theta1 theta2 theta3')
l1, l2, l3 = sp.symbols('l1 l2 l3')

f1_f0_T=np.array([[sp.cos(theta1), -sp.sin(theta1), 0],
             [sp.sin(theta1), sp.cos(theta1), 0],
             [0, 0, 1]])
f2_f1_T=np.array([[sp.cos(theta2), -sp.sin(theta2), l1],
            [sp.sin(theta2), sp.cos(theta2),0],
            [0, 0, 1]])
f3_f2_T=np.array([[sp.cos(theta3), -sp.sin(theta3), l2],
            [sp.sin(theta3), sp.cos(theta3),0],
            [0, 0, 1]])
f4_f3_T=np.array([[sp.cos(0), -sp.sin(0), l3],
            [sp.sin(0), sp.cos(0),0],
            [0, 0, 1]])
ee_bs_T=np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,f4_f3_T)))
ee_bs_T=sp.simplify(ee_bs_T) # Unfortunately, we do not get the simple
# expression on the wiki.
#print("ee_bs_T")
#display(ee_bs_T)

#For substituting in the following: 60,-30, 60 degree increments
#print("ee_bs_T after substitutions")
replacements=[(theta1,60*np.pi/180),(theta2,-30*np.pi/180), 
              (theta3,60*np.pi/180), (l1,1), (l2,1), (l3,1)]

#display(ee_bs_T.subs(replacements))

End_Coord=np.array([[0,0,1]])
End_Coord=End_Coord.T

#print("f1_f0_T")
f1_f0_T=sp.simplify(f1_f0_T)
#display(f1_f0_T.subs(replacements))
f1_f0_T=np.array(f1_f0_T.subs(replacements)).astype(np.float64)
f1_f0_T=np.reshape(f1_f0_T,(3,3))
print("f1_f0_T dot End_Coord")
display(np.dot(f1_f0_T,End_Coord))
Joint0=np.dot(f1_f0_T,End_Coord)

#print("\nf2_f1_T")
f2_f1_T=sp.simplify(f2_f1_T)
#display(f2_f1_T.subs(replacements))
f2_f1_T=np.array(f2_f1_T.subs(replacements)).astype(np.float64)
f2_f1_T=np.reshape(f2_f1_T,(3,3))
print("f2_f0_T dot End_Coord")
display(np.dot(f1_f0_T,np.dot(f2_f1_T,End_Coord)))
Joint1=np.dot(f1_f0_T,np.dot(f2_f1_T,End_Coord))

#print("\nf3_f2_T")
f3_f2_T=sp.simplify(f3_f2_T)
#display(f3_f2_T.subs(replacements))
f3_f2_T=np.array(f3_f2_T.subs(replacements)).astype(np.float64)
f3_f2_T=np.reshape(f3_f2_T,(3,3))
print("f3_f0_T dot End_Coord")
display(np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,End_Coord))))
Joint2=np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,End_Coord)))

#print("\nf4_f3_T")
f4_f3_T=sp.simplify(f4_f3_T)
#display(f4_f3_T.subs(replacements))
f4_f3_T=np.array(f4_f3_T.subs(replacements)).astype(np.float64)
f4_f3_T=np.reshape(f4_f3_T,(3,3))
print("f4_f0_T dot End_Coord")
display(np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,np.dot(f4_f3_T,End_Coord)))))
EndEffector=np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,np.dot(f4_f3_T,End_Coord))))

fig=plt.figure()
ax=fig.add_subplot(111)
plt.plot([Joint0[0][0], Joint1[0][0]],[Joint0[1][0],Joint1[1][0]],'bo-')
plt.plot([Joint1[0][0], Joint2[0][0]],[Joint1[1][0],Joint2[1][0]],'ro-')
plt.plot([Joint2[0][0], EndEffector[0][0]],
         [Joint2[1][0],EndEffector[1][0]],'go-')

ax.set_xlim([0, 1])
plt.axis('equal')
ax.set_xlabel('X',size=20)
ax.set_ylabel('Y',size=20)
plt.savefig('2D 60 neg30 60 rotations 200212.png', dpi=300, bbox_inches='tight')

Planar, three-link manipulator with $\theta _{1}=60^{o}$, $\theta _{2}=-30^{o}$, and $\theta _{3}=60^{o}$.

Kinematic Equations for a Serial Manipulating Robotic Arm

The kinematic equations for the series chain of a robot are obtained using a rigid transformation [Z] to characterize the relative movement allowed at each joint and separate rigid transformation [X] to define the dimensions of each link. The result is a sequence of rigid transformations alternating joint and link transformations from the base of the chain to its end link, which is equated to the specified position for the end link,

$[T]=[Z_{1}][X_{1}][Z_{2}][X_{2}]\ldots [X_{n-1}][Z_{n}][X_{n}],\!$

where [T] is the transformation locating the end-link. These equations are called the kinematics equations of the serial chain.

Denavit-Hartenberg Notation (Copied from Link and Link)

In 1955, Jacques Denavit and Richard Hartenberg introduced a convention for the definition of the joint matrices [Z] and link matrices [X] to standardize the coordinate frame for spatial linkages. This convention positions the joint frame so that it consists of a screw displacement along the Z-axis

$[Z_{i}]=\operatorname {Trans} _{Z_{i}}(d_{i})\operatorname {Rot} _{Z_{i}}(\theta _{i}),$

and it positions the link frame so it consists of a screw displacement along the X-axis,

$[X_{i}]=\operatorname {Trans} _{X_{i}}(a_{i,i+1})\operatorname {Rot} _{X_{i}}(\alpha _{i,i+1}).$

Using this notation, each transformation-link goes along a serial chain robot, and can be described by the coordinate transformation,

$_{i-1}^{i}T=[Z_{i}][X_{i}]=\operatorname {Trans} _{Z_{i}}(d_{i})\operatorname {Rot} _{Z_{i}}(\theta _{i})\operatorname {Trans} _{X_{i}}(a_{i,i+1})\operatorname {Rot} _{X_{i}}(\alpha _{i,i+1}),$

where θ_i, d_i, α_i,i+1 and a_i,i+1 are known as the Denavit-Hartenberg parameters.

Kinematics equations revisited

The kinematics equations of a serial chain of n links, with joint parameters θ_i are given by

$[T]=_{0}^{n}T=\prod _{i=1}^{n}{^{i}_{i-1}T(\theta _{i})},$

where $_{i-1}^{i}T(\theta _{i})$ is the transformation matrix from the frame of link $i$ to link $i-1$. In robotics, these are conventionally described by Denavit–Hartenberg parameters.

Denavit-Hartenberg matrix

The matrices associated with these operations are:

$\operatorname {Trans} _{Z_{i}}(d_{i})={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&d_{i}\\0&0&0&1\end{bmatrix}},\quad \operatorname {Rot} _{Z_{i}}(\theta _{i})={\begin{bmatrix}\cos \theta _{i}&-\sin \theta _{i}&0&0\\\sin \theta _{i}&\cos \theta _{i}&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}.$

Similarly,

$\operatorname {Trans} _{X_{i}}(a_{i,i+1})={\begin{bmatrix}1&0&0&a_{i,i+1}\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}},\quad \operatorname {Rot} _{X_{i}}(\alpha _{i,i+1})={\begin{bmatrix}1&0&0&0\\0&\cos \alpha _{i,i+1}&-\sin \alpha _{i,i+1}&0\\0&\sin \alpha _{i,i+1}&\cos \alpha _{i,i+1}&0\\0&0&0&1\end{bmatrix}}.$

The use of the Denavit-Hartenberg convention yields the link transformation matrix, [ⁱ_i-1T] as

${^{i}}_{i-1}T={\begin{bmatrix}\cos \theta _{i}&-\sin \theta _{i}\cos \alpha _{i,i+1}&\sin \theta _{i}\sin \alpha _{i,i+1}&a_{i,i+1}\cos \theta _{i}\\\sin \theta _{i}&\cos \theta _{i}\cos \alpha _{i,i+1}&-\cos \theta _{i}\sin \alpha _{i,i+1}&a_{i,i+1}\sin \theta _{i}\\0&\sin \alpha _{i,i+1}&\cos \alpha _{i,i+1}&d_{i}\\0&0&0&1\end{bmatrix}},$

known as the Denavit-Hartenberg matrix.

Denavit-Hartenberg Notation Re-visited

In mechanical engineering, the Denavit–Hartenberg parameters (also called DH parameters) are the four parameters associated with a particular convention for attaching reference frames to the links of a spatial kinematic chain, or robot manipulator.

Jacques Denavit and Richard Hartenberg introduced this convention in 1955 in order to standardize the coordinate frames for spatial linkages.

Richard Paul demonstrated its value for the kinematic analysis of robotic systems in 1981. While many conventions for attaching reference frames have been developed, the Denavit–Hartenberg convention remains a popular approach.

Denavit–Hartenberg Convention and Transformations

A commonly used convention for selecting frames of reference in robotics applications is the Denavit and Hartenberg (D–H) convention which was introduced by Jacques Denavit and Richard S. Hartenberg. In this convention, coordinate frames are attached to the joints between two links such that one transformation is associated with the joint, [Z], and the second is associated with the link [X]. The coordinate transformations along a serial robot consisting of n links form the kinematics equations of the robot,

$[T]=[Z_{1}][X_{1}][Z_{2}][X_{2}]\ldots [X_{n-1}][Z_{n}][X_{n}],\!$

where [T] is the transformation locating the end-link.

In order to determine the coordinate transformations [Z] and [X], the joints connecting the links are modeled as either hinged or sliding joints, each of which have a unique line S in space that forms the joint axis and define the relative movement of the two links. A typical serial robot is characterized by a sequence of six lines S_i, i = 1,...,6, one for each joint in the robot. For each sequence of lines S_i and S_i+1, there is a common normal line A_i,i+1. The system of six joint axes S_i and five common normal lines A_i,i+1 form the kinematic skeleton of the typical six degree of freedom serial robot. Denavit and Hartenberg introduced the convention that Z coordinate axes are assigned to the joint axes S_i and X coordinate axes are assigned to the common normals A_i,i+1.

This convention allows the definition of the movement of links around a common joint axis S_i by the screw displacement,

$[Z_{i}]={\begin{bmatrix}\cos \theta _{i}&-\sin \theta _{i}&0&0\\\sin \theta _{i}&\cos \theta _{i}&0&0\\0&0&1&d_{i}\\0&0&0&1\end{bmatrix}},$

where θ_i is the rotation around and d_i is the slide along the Z axis—either of the parameters can be constants depending on the structure of the robot. Under this convention the dimensions of each link in the serial chain are defined by the screw displacement around the common normal A_i,i+1 from the joint S_i to S_i+1, which is given by

$[X_{i}]={\begin{bmatrix}1&0&0&a_{i,i+1}\\0&\cos \alpha _{i,i+1}&-\sin \alpha _{i,i+1}&0\\0&\sin \alpha _{i,i+1}&\cos \alpha _{i,i+1}&0\\0&0&0&1\end{bmatrix}},$

where α_i,i+1 and r_i,i+1 define the physical dimensions of the link in terms of the angle measured around and distance measured along the X axis.

In summary, the reference frames are laid out as follows:

1. the $z$-axis is in the direction of the joint axis
2. the $x$-axis is parallel to the common normal: $x_{n}=z_{n}\times z_{n-1}$ (or away from zn-1)
   If there is no unique common normal (parallel $z$ axes), then $d$ (below) is a free parameter. The direction of $x_{n}$ is from $z_{n-1}$ to $z_{n}$, as shown in the video below.
3. the $y$-axis follows from the $x$- and $z$-axis by choosing it to be a right-handed coordinate system.

Four parameters

The four parameters of classic DH convention are shown in red text, which are $\theta _{i},d_{i},a_{i},\alpha _{i}$. With those four parameters, we can translate the coordinates from $O_{i-1}X_{i-1}Y_{i-1}Z_{i-1}$ to $O_{i}X_{i}Y_{i}Z_{i}$.

The following four transformation parameters are known as D–H parameters:.

• $d\,$: offset along previous $z$ to the common normal
• $\theta \,$: angle about previous $z$, from old $x$ to new $x$
• $a\,$: length of the common normal (do not confuse with $\alpha$). Assuming a revolute joint, this is the radius about previous $z$.
• $\alpha \,$: angle about common normal, from old $z$ axis to new $z$ axis

A visualization of D–H parameterization is available: YouTube

There is some choice in frame layout as to whether the previous $x$ axis or the next $x$ points along the common normal. The latter system allows branching chains more efficiently, as multiple frames can all point away from their common ancestor, but in the alternative layout the ancestor can only point toward one successor. Thus the commonly used notation places each down-chain $x$ axis collinear with the common normal, yielding the transformation calculations shown below.

We can note constraints on the relationships between the axes:

• the $x_{n}$-axis is perpendicular to both the $z_{n-1}$ and $z_{n}$ axes
• the $x_{n}$-axis intersects both $z_{n-1}$ and $z_{n}$ axes
• the origin of joint $n$ is at the intersection of $x_{n}$ and $z_{n}$
• $y_{n}$ completes a right-handed reference frame based on $x_{n}$ and $z_{n}$

Denavit–Hartenberg matrix

It is common to separate a screw displacement into the product of a pure translation along a line and a pure rotation about the line, so that

$[Z_{i}]=\operatorname {Trans} _{Z_{i}}(d_{i})\operatorname {Rot} _{Z_{i}}(\theta _{i}),$

and

$[X_{i}]=\operatorname {Trans} _{X_{i}}(a_{i,i+1})\operatorname {Rot} _{X_{i}}(\alpha _{i,i+1}).$

Using this notation, each link can be described by a coordinate transformation from the concurrent coordinate system to the previous coordinate system.

${^{n}}_{n-1}T=\operatorname {Trans} _{z_{n-1}}(d_{n})\cdot \operatorname {Rot} _{z_{n-1}}(\theta _{n})\cdot \operatorname {Trans} _{x_{n}}(r_{n})\cdot \operatorname {Rot} _{x_{n}}(\alpha _{n})$

Note that this is the product of two screw displacements, The matrices associated with these operations are:

$\operatorname {Trans} _{z_{n-1}}(d_{n})=\left[{\begin{array}{ccc|c}1&0&0&0\\0&1&0&0\\0&0&1&d_{n}\\\hline 0&0&0&1\end{array}}\right]$

$\operatorname {Rot} _{z_{n-1}}(\theta _{n})=\left[{\begin{array}{ccc|c}\cos \theta _{n}&-\sin \theta _{n}&0&0\\\sin \theta _{n}&\cos \theta _{n}&0&0\\0&0&1&0\\\hline 0&0&0&1\end{array}}\right]$

$\operatorname {Trans} _{x_{n}}(a_{n})=\left[{\begin{array}{ccc|c}1&0&0&a_{n}\\0&1&0&0\\0&0&1&0\\\hline 0&0&0&1\end{array}}\right]$

$\operatorname {Rot} _{x_{n}}(\alpha _{n})=\left[{\begin{array}{ccc|c}1&0&0&0\\0&\cos \alpha _{n}&-\sin \alpha _{n}&0\\0&\sin \alpha _{n}&\cos \alpha _{n}&0\\\hline 0&0&0&1\end{array}}\right]$

This gives:

$\operatorname {^{n}} _{n-1}T=\left[{\begin{array}{ccc|c}\cos \theta _{n}&-\sin \theta _{n}\cos \alpha _{n}&\sin \theta _{n}\sin \alpha _{n}&a_{n}\cos \theta _{n}\\\sin \theta _{n}&\cos \theta _{n}\cos \alpha _{n}&-\cos \theta _{n}\sin \alpha _{n}&a_{n}\sin \theta _{n}\\0&\sin \alpha _{n}&\cos \alpha _{n}&d_{n}\\\hline 0&0&0&1\end{array}}\right]=\left[{\begin{array}{ccc|c}&&&\\&R&&T\\&&&\\\hline 0&0&0&1\end{array}}\right]$

where R is the 3×3 submatrix describing rotation and T is the 3×1 submatrix describing translation.

In some books, the order of transformation for a pair of consecutive rotation and translation (such as $d_{n}$and $\theta _{n}$) is replaced. However, because matrix multiplication order for such pair does not matter, the result is the same. For example: $\operatorname {Trans} _{z_{n-1}}(d_{n})\cdot \operatorname {Rot} _{z_{n-1}}(\theta _{n})=\operatorname {Rot} _{z_{n-1}}(\theta _{n})\cdot \operatorname {Trans} _{z_{n-1}}(d_{n})$.

Use of Denavit and Hartenberg matrices

The Denavit and Hartenberg notation gives a standard methodology to write the kinematic equations of a manipulator. This is especially useful for serial manipulators where a matrix is used to represent the pose (position and orientation) of one body with respect to another.

The position of body $n$ with respect to $n-1$ may be represented by a position matrix indicated with the symbol $T$ or $M$

$\operatorname {^{n}} _{n-1}T=M_{n-1,n}$

This matrix is also used to transform a point from frame $n$ to $n-1$

$M_{n-1,n}=\left[{\begin{array}{ccc|c}R_{xx}&R_{xy}&R_{xz}&T_{x}\\R_{yx}&R_{yy}&R_{yz}&T_{y}\\R_{zx}&R_{zy}&R_{zz}&T_{z}\\\hline 0&0&0&1\end{array}}\right]$

Where the upper left $3\times 3$ submatrix of $M$ represents the relative orientation of the two bodies, and the upper right $3\times 1$ represents their relative position or more specifically the body position in frame n − 1 represented with element of frame n.

The position of body $k$ with respect to body $i$ can be obtained as the product of the matrices representing the pose of $j$ with respect of $i$ and that of $k$ with respect of $j$

$M_{i,k}=M_{i,j}M_{j,k}$

An important property of Denavit and Hartenberg matrices is that the inverse is

$M^{-1}=\left[{\begin{array}{ccc|c}&&&\\&R^{T}&&-R^{T}T\\&&&\\\hline 0&0&0&1\end{array}}\right]$

where $R^{T}$ is both the transpose and the inverse of the orthogonal matrix $R$, i.e. $R_{ij}^{-1}=R_{ij}^{T}=R_{ji}$.

Example of Planar, Three-link Manipulator with D-H Parameters

Planar, three-link manipulator with described D-H Parameters.

D-H Parameters for planar manipulator with three links

Link 1: $d_{1}=0$, $\theta _{1}=\theta _{1}$, $a_{1}=l_{1}$, and $\alpha _{1}=0$

Link 2: $d_{2}=0$, $\theta _{2}=\theta _{2}$, $a_{2}=l_{2}$, and $\alpha _{2}=0$

Link 3: $d_{3}=0$, $\theta _{3}=\theta _{3}$, $a_{3}=l_{3}$, and $\alpha _{3}=0$

Code

%reset -f
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt

#All the joints set to angles of 45 degrees.
#Link 1
d1=0; theta1=45*np.pi/180; a1=1; alpha1=0
#Link 2
d2=0; theta2=0*np.pi/180; a2=1; alpha2=0
#Link 3
d3=0; theta3=45*np.pi/180; a3=1; alpha3=0

Link2_1_T=np.array([[np.cos(theta1), -np.sin(theta1)*np.cos(alpha1), np.sin(theta1)*np.sin(alpha1), a1*np.cos(theta1)],
                [np.sin(theta1), np.cos(theta1)*np.cos(alpha1), -np.cos(theta1)*np.sin(alpha1), a1*np.sin(theta1)],
                [0, np.sin(alpha1), np.cos(alpha1), d1],
                [0, 0, 0, 1]])
Link3_2_T=np.array([[np.cos(theta2), -np.sin(theta2)*np.cos(alpha2), np.sin(theta2)*np.sin(alpha2), a2*np.cos(theta2)],
                [np.sin(theta2), np.cos(theta2)*np.cos(alpha2), -np.cos(theta2)*np.sin(alpha2), a2*np.sin(theta2)],
                [0, np.sin(alpha2), np.cos(alpha2), d2],
                [0, 0, 0, 1]])
Link4_3_T=np.array([[np.cos(theta3), -np.sin(theta3)*np.cos(alpha3), np.sin(theta3)*np.sin(alpha3), a3*np.cos(theta3)],
                [np.sin(theta3), np.cos(theta3)*np.cos(alpha3), -np.cos(theta3)*np.sin(alpha3), a3*np.sin(theta3)],
                [0, np.sin(alpha3), np.cos(alpha3), d3],
                [0, 0, 0, 1]])

End_Coord=np.array([[0,0,0,1]])
End_Coord=End_Coord.T

Joint1Link0=End_Coord
Joint2Link1=np.dot(Link2_1_T,End_Coord)
Joint3Link2=np.dot(Link2_1_T,np.dot(Link3_2_T,End_Coord))
Joint4Link3=np.dot(Link2_1_T,np.dot(Link3_2_T,np.dot(Link4_3_T,End_Coord)))

fig=plt.figure()
ax=fig.add_subplot(111)
plt.plot([Joint1Link0[0][0], Joint2Link1[0][0]],
         [Joint1Link0[1][0], Joint2Link1[1][0]],'bo-')
plt.plot([Joint2Link1[0][0], Joint3Link2[0][0]],
         [Joint2Link1[1][0], Joint3Link2[1][0]],'ro-')
plt.plot([Joint3Link2[0][0], Joint4Link3[0][0]],
         [Joint3Link2[1][0], Joint4Link3[1][0]],'go-')

ax.set_xlim([0, 1])
plt.axis('equal')
ax.set_xlabel('X',size=20)
ax.set_ylabel('Y',size=20)
plt.savefig('PlanarThreeLinkManipulatorDH.png',dpi=300,bbox_inches='tight')

Animated Example of the Top-Down Perspective of a Three-link Manipulator with D-H Parameters

Animation of a three-link, serial manipulator described with D-H notation.

D-H Parameters for serial manipulator with three links

Link 1: $d_{1}=0.1$, $\theta _{1}=\theta _{1}$, $a_{1}=l_{1}$, and $\alpha _{1}=0$

Link 2: $d_{2}=0.1$, $\theta _{2}=\theta _{2}$, $a_{2}=l_{2}$, and $\alpha _{2}=0$

Link 3: $d_{3}=0.1$, $\theta _{3}=\theta _{3}$, $a_{3}=l_{3}$, and $\alpha _{3}=0$

We vary $\theta _{1}$ from 0 to 45 degrees over 10 frames while the other joint angles remain constant with $\theta _{2}=0$ and $\theta _{3}=45^{o}$.

Code

%reset -f
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import os

#Make sure you create the ImageDirectory (mkdir) before running
ImageDirectory="Session11_Linux_Animation"
ImageName="Linux_test"
VideoName="DH_2D_animation_200302"
FrameTime=50 #100ths of a second

for ImageNum in range(0,10,1):
    #Link 1
    d1=0.1; theta1=ImageNum*5*np.pi/180; a1=1; alpha1=0
    #Link 2
    d2=0.1; theta2=0*np.pi/180; a2=1; alpha2=0
    #Link 3
    d3=0.1; theta3=45*np.pi/180; a3=1; alpha3=0
    
    Link2_1_T=np.array([[np.cos(theta1), -np.sin(theta1)*np.cos(alpha1), np.sin(theta1)*np.sin(alpha1), a1*np.cos(theta1)],
                [np.sin(theta1), np.cos(theta1)*np.cos(alpha1), -np.cos(theta1)*np.sin(alpha1), a1*np.sin(theta1)],
                [0, np.sin(alpha1), np.cos(alpha1), d1],
                [0, 0, 0, 1]])
    Link3_2_T=np.array([[np.cos(theta2), -np.sin(theta2)*np.cos(alpha2), np.sin(theta2)*np.sin(alpha2), a2*np.cos(theta2)],
                [np.sin(theta2), np.cos(theta2)*np.cos(alpha2), -np.cos(theta2)*np.sin(alpha2), a2*np.sin(theta2)],
                [0, np.sin(alpha2), np.cos(alpha2), d2],
                [0, 0, 0, 1]])
    Link4_3_T=np.array([[np.cos(theta3), -np.sin(theta3)*np.cos(alpha3), np.sin(theta3)*np.sin(alpha3), a3*np.cos(theta3)],
                [np.sin(theta3), np.cos(theta3)*np.cos(alpha3), -np.cos(theta3)*np.sin(alpha3), a3*np.sin(theta3)],
                [0, np.sin(alpha3), np.cos(alpha3), d3],
                [0, 0, 0, 1]])
    
    End_Coord=np.array([[0,0,0,1]])
    End_Coord=End_Coord.T
    
    ## Find the missing joints on the previous link
    End_Coord_for_Joint1Link1=np.transpose(np.array([[-a1,0,0,1]]))
    End_Coord_for_Joint2Link2=np.transpose(np.array([[-a2,0,0,1]]))
    End_Coord_for_Joint3Link3=np.transpose(np.array([[-a3,0,0,1]]))
    
    
    Joint1Link0=End_Coord
    Joint2Link1=np.dot(Link2_1_T,End_Coord)
    Joint3Link2=np.dot(Link2_1_T,np.dot(Link3_2_T,End_Coord))
    Joint4Link3=np.dot(Link2_1_T,np.dot(Link3_2_T,np.dot(Link4_3_T,End_Coord)))
    
    #New Joint Calculations
    Joint1Link1=np.dot(Link2_1_T,End_Coord_for_Joint1Link1)
    Joint2Link2=np.dot(Link2_1_T,np.dot(Link3_2_T,End_Coord_for_Joint2Link2))
    Joint3Link3=np.dot(Link2_1_T,np.dot(Link3_2_T,np.dot(Link4_3_T,End_Coord_for_Joint3Link3)))
    
    fig=plt.figure()
    ax=fig.add_subplot(111)
    plt.plot([Joint1Link1[0][0], Joint2Link1[0][0]],
         [Joint1Link1[1][0], Joint2Link1[1][0]],'bo-')
    plt.plot([Joint2Link2[0][0], Joint3Link2[0][0]],
         [Joint2Link2[1][0], Joint3Link2[1][0]],'ro-')
    plt.plot([Joint3Link3[0][0], Joint4Link3[0][0]],
         [Joint3Link3[1][0], Joint4Link3[1][0]],'go-')
    ax.set_xlim([-0.5, 3])
    ax.set_xbound([-0.5,3])
    ax.set_ylim([-0.5, 3])
    ax.set_ybound([-0.5, 3])
    #plt.axis('equal')
    plt.gca().set_aspect("equal", adjustable="box")
    ax.set_xlabel('X',size=20)
    ax.set_ylabel('Y',size=20)
    ax.set_autoscale_on(False)
    ax.set_title('Theta_1='+str(ImageNum*5)+' deg; Theta_3=45 deg', size=12)
    #Jae and Jess, thank you for helping improve the look of the plots.
    

    #There are automatic ways to make a directory, but go ahead and
    #make an appropriate directory instead of using some of these tricks:
    # https://stackoverflow.com/questions/11373610/save-matplotlib-file-to-a-directory
    plt.savefig(ImageDirectory+"/"+ImageName+str(ImageNum),dpi=300, bbox_inches='tight')

# If running windows, be sure to install ImageMagick before running this code.
if os.name=='nt':
    os.system("magick -delay "+str(FrameTime)+" "+ImageDirectory+"/"+ImageName+"*.png"+" "+ImageDirectory+"/"+VideoName+".gif")

if os.name=='posix':
    os.system("convert -delay "+str(FrameTime)+" "+ImageDirectory+"/"+ImageName+"*.png"+" "+ImageDirectory+"/"+VideoName+".gif")

3D Example of a Three-link Manipulator with D-H Parameters

3D representation of a pose of a three-link, serial manipulator.

D-H Parameters for serial manipulator with three links

Link 1: $d_{1}=0.1$, $\theta _{1}=45^{o}$, $a_{1}=l_{1}$, and $\alpha _{1}=0$

Link 2: $d_{2}=0.1$, $\theta _{2}=45^{o}$, $a_{2}=l_{2}$, and $\alpha _{2}=0$

Link 3: $d_{3}=0.1$, $\theta _{3}=45^{o}$, $a_{3}=l_{3}$, and $\alpha _{3}=0$

We use D-H notation, but we have to perform "extra" calculations to determine the locations of Joint 1 on Link 1 (J1L1), Joint 2 on Link 2 (J2L2), and Joint 3 on Link 3 (J3L3). One way to envision their locations (Joint $i$ on Link $i$) relative to the Joint $i+1$ on link $i$ is to remember them as being offset by $a_{i}$. Thus, we can find the location of Joint 1 on Link 1 in the global reference frame with the following D-H transformation:

$_{1}p_{1}=_{1}^{2}T{\begin{bmatrix}-a_{1}\\0\\0\\1\end{bmatrix}}$

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

#All the joints set to angles of 45 degrees.
#Link 1
d1=0.1; theta1=45*np.pi/180; a1=1; alpha1=0
#Link 2
d2=0.1; theta2=45*np.pi/180; a2=1; alpha2=0
#Link 3
d3=0.1; theta3=45*np.pi/180; a3=1; alpha3=0

Link2_1_T=np.array([[np.cos(theta1), -np.sin(theta1)*np.cos(alpha1), np.sin(theta1)*np.sin(alpha1), a1*np.cos(theta1)],
                [np.sin(theta1), np.cos(theta1)*np.cos(alpha1), -np.cos(theta1)*np.sin(alpha1), a1*np.sin(theta1)],
                [0, np.sin(alpha1), np.cos(alpha1), d1],
                [0, 0, 0, 1]])
Link3_2_T=np.array([[np.cos(theta2), -np.sin(theta2)*np.cos(alpha2), np.sin(theta2)*np.sin(alpha2), a2*np.cos(theta2)],
                [np.sin(theta2), np.cos(theta2)*np.cos(alpha2), -np.cos(theta2)*np.sin(alpha2), a2*np.sin(theta2)],
                [0, np.sin(alpha2), np.cos(alpha2), d2],
                [0, 0, 0, 1]])
Link4_3_T=np.array([[np.cos(theta3), -np.sin(theta3)*np.cos(alpha3), np.sin(theta3)*np.sin(alpha3), a3*np.cos(theta3)],
                [np.sin(theta3), np.cos(theta3)*np.cos(alpha3), -np.cos(theta3)*np.sin(alpha3), a3*np.sin(theta3)],
                [0, np.sin(alpha3), np.cos(alpha3), d3],
                [0, 0, 0, 1]])

End_Coord=np.array([[0,0,0,1]])
End_Coord=End_Coord.T

## Find the missing joints on the previous link
End_Coord_for_Joint1Link1=np.transpose(np.array([[-a1,0,0,1]]))
End_Coord_for_Joint2Link2=np.transpose(np.array([[-a2,0,0,1]]))
End_Coord_for_Joint3Link3=np.transpose(np.array([[-a3,0,0,1]]))


Joint1Link0=End_Coord
print("Joint1Link0:\n",Joint1Link0)
Joint2Link1=np.dot(Link2_1_T,End_Coord)
Joint3Link2=np.dot(Link2_1_T,np.dot(Link3_2_T,End_Coord))
Joint4Link3=np.dot(Link2_1_T,np.dot(Link3_2_T,np.dot(Link4_3_T,End_Coord)))

#New Joint Calculations
Joint1Link1=np.dot(Link2_1_T,End_Coord_for_Joint1Link1)
print("Joint1Link1:\n",Joint1Link1)
Joint2Link2=np.dot(Link2_1_T,np.dot(Link3_2_T,End_Coord_for_Joint2Link2))
Joint3Link3=np.dot(Link2_1_T,np.dot(Link3_2_T,np.dot(Link4_3_T,End_Coord_for_Joint3Link3)))


fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')

ax.plot([Joint1Link0[0][0]], [Joint1Link0[1][0]],[Joint1Link0[2][0]],'c*')
ax.plot([Joint1Link1[0][0], Joint2Link1[0][0]],
         [Joint1Link1[1][0], Joint2Link1[1][0]],
        [Joint1Link1[2][0], Joint2Link1[2][0]],'bo-')
ax.text(Joint1Link0[0][0]+0.1, Joint1Link0[1][0], Joint1Link0[2][0],
        'J1L0',None,size=12)
    
ax.plot([Joint2Link2[0][0], Joint3Link2[0][0]],
         [Joint2Link2[1][0], Joint3Link2[1][0]],
        [Joint2Link2[2][0], Joint3Link2[2][0]],'ro-')
ax.text(Joint1Link1[0][0]+0.1, Joint1Link1[1][0], Joint1Link1[2][0],
        'J1L1',None,size=12)
ax.text(Joint2Link1[0][0]+0.1, Joint2Link1[1][0], Joint2Link1[2][0],
        'J2L1',None,size=12)
    
ax.plot([Joint3Link3[0][0], Joint4Link3[0][0]],
         [Joint3Link3[1][0], Joint4Link3[1][0]],
        [Joint3Link3[2][0], Joint4Link3[2][0]],'go-')
plt.plot([Joint4Link3[0][0]],
         [Joint4Link3[1][0]],
         [Joint4Link3[2][0]],'c*')
ax.text(Joint2Link2[0][0]+0.1, Joint2Link2[1][0], Joint2Link2[2][0],
        'J2L2',None,size=12)
ax.text(Joint3Link2[0][0]+0.1, Joint3Link2[1][0], Joint3Link2[2][0],
        'J3L2',None,size=12)
ax.text(Joint3Link3[0][0]+0.1, Joint3Link3[1][0], Joint3Link3[2][0],
        'J3L3',None,size=12)
ax.text(Joint4Link3[0][0]+0.1, Joint4Link3[1][0], Joint4Link3[2][0],
        'J4L3',None,size=12)
    
ax.set_xlabel('X',size=20)
ax.set_ylabel('Y',size=20)
ax.set_zlabel('Z',size=20)
ax.set_xlim([-0.25,3])
ax.set_ylim([-0.25,3])
    
ax.view_init(30,-115)
ax.set_title('Theta_1,Theta_2,Theta_3=45 deg', size=12)

plt.savefig('Stationary_DH_200302.png',dpi=300, bbox_inches='tight')

3D Example of an Animated, Three-link Manipulator with D-H Parameters

3D animation of a three-link, serial manipulator using D-H parameters.

D-H Parameters for a serial manipulator with three links

Link 1: $d_{1}=0.1$, $\theta _{1}=\theta _{1}$, $a_{1}=l_{1}$, and $\alpha _{1}=0$

Link 2: $d_{2}=0.1$, $\theta _{2}=\theta _{2}$, $a_{2}=l_{2}$, and $\alpha _{2}=0$

Link 3: $d_{3}=0.1$, $\theta _{3}=\theta _{3}$, $a_{3}=l_{3}$, and $\alpha _{3}=0$

We vary $\theta _{1}$, $\theta _{2}$, and $\theta _{3}$ from 0 to 45 degrees over 10 frames.

Code

%reset -f
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
import os
ImageDirectory="Session11_3DAnimation"
ImageName="test"
VideoName="DH_3D_animation_200302"
FrameTime=75 #100ths of a second

for ImageNum in range(0,10,1):
    #All the joints set to angles varying from 0-45 degrees.
    #Link 1
    d1=0.1; theta1=ImageNum*5*np.pi/180; a1=1; alpha1=0
    #Link 2
    d2=0.1; theta2=ImageNum*5*np.pi/180; a2=1; alpha2=0
    #Link 3
    d3=0.1; theta3=ImageNum*5*np.pi/180; a3=1; alpha3=0
    
    Link2_1_T=np.array([[np.cos(theta1), -np.sin(theta1)*np.cos(alpha1), np.sin(theta1)*np.sin(alpha1), a1*np.cos(theta1)],
                [np.sin(theta1), np.cos(theta1)*np.cos(alpha1), -np.cos(theta1)*np.sin(alpha1), a1*np.sin(theta1)],
                [0, np.sin(alpha1), np.cos(alpha1), d1],
                [0, 0, 0, 1]])
    Link3_2_T=np.array([[np.cos(theta2), -np.sin(theta2)*np.cos(alpha2), np.sin(theta2)*np.sin(alpha2), a2*np.cos(theta2)],
                [np.sin(theta2), np.cos(theta2)*np.cos(alpha2), -np.cos(theta2)*np.sin(alpha2), a2*np.sin(theta2)],
                [0, np.sin(alpha2), np.cos(alpha2), d2],
                [0, 0, 0, 1]])
    Link4_3_T=np.array([[np.cos(theta3), -np.sin(theta3)*np.cos(alpha3), np.sin(theta3)*np.sin(alpha3), a3*np.cos(theta3)],
                [np.sin(theta3), np.cos(theta3)*np.cos(alpha3), -np.cos(theta3)*np.sin(alpha3), a3*np.sin(theta3)],
                [0, np.sin(alpha3), np.cos(alpha3), d3],
                [0, 0, 0, 1]])
    
    End_Coord=np.array([[0,0,0,1]])
    End_Coord=End_Coord.T
    
    ## Find the missing joints on the previous link
    End_Coord_for_Joint1Link1=np.transpose(np.array([[-a1,0,0,1]]))
    End_Coord_for_Joint2Link2=np.transpose(np.array([[-a2,0,0,1]]))
    End_Coord_for_Joint3Link3=np.transpose(np.array([[-a3,0,0,1]]))
    
    
    Joint1Link0=End_Coord
    # print("Joint1Link0:\n",Joint1Link0)
    Joint2Link1=np.dot(Link2_1_T,End_Coord)
    Joint3Link2=np.dot(Link2_1_T,np.dot(Link3_2_T,End_Coord))
    Joint4Link3=np.dot(Link2_1_T,np.dot(Link3_2_T,np.dot(Link4_3_T,End_Coord)))
    
    #New Joint Calculations
    Joint1Link1=np.dot(Link2_1_T,End_Coord_for_Joint1Link1)
    #print("Joint1Link1:\n",Joint1Link1)
    Joint2Link2=np.dot(Link2_1_T,np.dot(Link3_2_T,End_Coord_for_Joint2Link2))
    Joint3Link3=np.dot(Link2_1_T,np.dot(Link3_2_T,np.dot(Link4_3_T,End_Coord_for_Joint3Link3)))
    
    
    fig=plt.figure()
    ax=fig.add_subplot(111,projection='3d')
    
    ax.plot([Joint1Link0[0][0]], [Joint1Link0[1][0]],[Joint1Link0[2][0]],'c*')
    ax.plot([Joint1Link1[0][0], Joint2Link1[0][0]],
         [Joint1Link1[1][0], Joint2Link1[1][0]],
        [Joint1Link1[2][0], Joint2Link1[2][0]],'bo-')
    ax.text(Joint1Link0[0][0]+0.1, Joint1Link0[1][0], Joint1Link0[2][0],
        'J1L0',None,size=12)
    
    ax.plot([Joint2Link2[0][0], Joint3Link2[0][0]],
         [Joint2Link2[1][0], Joint3Link2[1][0]],
        [Joint2Link2[2][0], Joint3Link2[2][0]],'ro-')
    ax.text(Joint1Link1[0][0]+0.1, Joint1Link1[1][0], Joint1Link1[2][0],
        'J1L1',None,size=12)
    ax.text(Joint2Link1[0][0]+0.1, Joint2Link1[1][0], Joint2Link1[2][0],
        'J2L1',None,size=12)
    
    ax.plot([Joint3Link3[0][0], Joint4Link3[0][0]],
         [Joint3Link3[1][0], Joint4Link3[1][0]],
        [Joint3Link3[2][0], Joint4Link3[2][0]],'go-')
    plt.plot([Joint4Link3[0][0]],
         [Joint4Link3[1][0]],
         [Joint4Link3[2][0]],'c*')
    ax.text(Joint2Link2[0][0]+0.1, Joint2Link2[1][0], Joint2Link2[2][0],
        'J2L2',None,size=12)
    ax.text(Joint3Link2[0][0]+0.1, Joint3Link2[1][0], Joint3Link2[2][0],
        'J3L2',None,size=12)
    ax.text(Joint3Link3[0][0]+0.1, Joint3Link3[1][0], Joint3Link3[2][0],
        'J3L3',None,size=12)
    ax.text(Joint4Link3[0][0]+0.1, Joint4Link3[1][0], Joint4Link3[2][0],
        'J4L3',None,size=12)
    
    ax.set_xlabel('X',size=20)
    ax.set_ylabel('Y',size=20)
    ax.set_zlabel('Z',size=20)
    ax.set_xlim([-0.25,3])
    ax.set_ylim([-0.25,3])
    
    ax.view_init(30,-115)
    ax.set_title('Theta_1,Theta_2,Theta_3='+str(ImageNum*5)+' deg', size=12)

    plt.savefig(ImageDirectory+"/"+ImageName+str(ImageNum),dpi=300, bbox_inches='tight')


# If running windows, be sure to install ImageMagick before running this code.    
if os.name=='nt':
    os.system("magick -delay "+str(FrameTime)+" "+ImageDirectory+"/"+ImageName+"*.png"+" "+ImageDirectory+"/"+VideoName+".gif")

if os.name=='posix':
    os.system("convert -delay "+str(FrameTime)+" "+ImageDirectory+"/"+ImageName+"*.png"+" "+ImageDirectory+"/"+VideoName+".gif")

Addtional Examples for Denavit-Hartenberg Parameters

Additional Examples for Denavit-Hartenberg Parameters

Modified DH parameters

Some books such as Introduction to Robotics: Mechanics and Control (3rd Edition) use modified DH parameters. The difference between the classic DH parameters and the modified DH parameters are the locations of the coordinates system attachment to the links and the order of the performed transformations.

Modified DH parameters

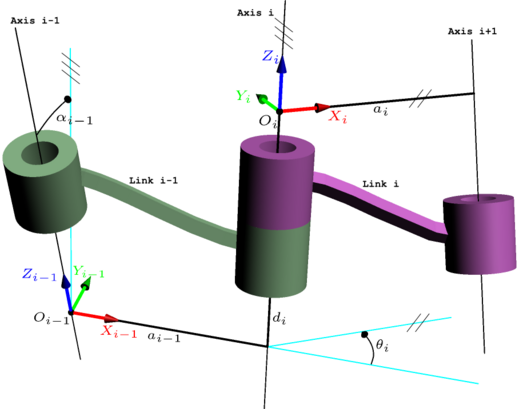
Compared with the classic DH parameters, the coordinates of frame $O_{i-1}$ is put on axis i − 1, not the axis i in classic DH convention. The coordinates of $O_{i}$ is put on the axis i, not the axis i + 1 in classic DH convention.

Another difference is that according to the modified convention, the transform matrix is given by the following order of operations:

${^{n}}_{n-1}T=\operatorname {Rot} _{x_{n-1}}(\alpha _{n-1})\cdot \operatorname {Trans} _{x_{n-1}}(a_{n-1})\cdot \operatorname {Rot} _{z_{n}}(\theta _{n})\cdot \operatorname {Trans} _{z_{n}}(d_{n})$

Thus, the matrix of the modified DH parameters becomes

$\operatorname {^{n}} _{n-1}T=\left[{\begin{array}{ccc|c}\cos \theta _{n}&-\sin \theta _{n}&0&a_{n-1}\\\sin \theta _{n}\cos \alpha _{n-1}&\cos \theta _{n}\cos \alpha _{n-1}&-\sin \alpha _{n-1}&-d_{n}\sin \alpha _{n-1}\\\sin \theta _{n}\sin \alpha _{n-1}&\cos \theta _{n}\sin \alpha _{n-1}&\cos \alpha _{n-1}&d_{n}\cos \alpha _{n-1}\\\hline 0&0&0&1\end{array}}\right]$

Note that some books (e.g.:) use $a_{n}$ and $\alpha _{n}$ to indicate the length and twist of link n − 1 rather than link n. As a consequence, ${}^{n-1}T_{n}$ is formed only with parameters using the same subscript.

In some books, the order of transformation for a pair of consecutive rotation and translation (such as $d_{n}$and $\theta _{n}$) is replaced. However, because matrix multiplication order for such pair does not matter, the result is the same. For example: $\operatorname {Trans} _{z_{n}}(d_{n})\cdot \operatorname {Rot} _{z_{n}}(\theta _{n})=\operatorname {Rot} _{z_{n}}(\theta _{n})\cdot \operatorname {Trans} _{z_{n}}(d_{n})$.

Surveys of DH conventions and its differences have been published.

Velocity and Acceleration in Kinematics

Further matrices can be defined to represent velocity and acceleration of bodies. The velocity of body $i$ with respect to body $j$ can be represented in frame $k$ by the matrix

$W_{i,j(k)}=\left[{\begin{array}{ccc|c}0&-\omega _{z}&\omega _{y}&v_{x}\\\omega _{z}&0&-\omega _{x}&v_{y}\\-\omega _{y}&\omega _{x}&0&v_{z}\\\hline 0&0&0&0\end{array}}\right]$

where $\omega$ is the angular velocity of body $j$ with respect to body $i$ and all the components are expressed in frame $k$; $v$ is the velocity of one point of body $j$ with respect to body $i$ (the pole). The pole is the point of $j$ passing through the origin of frame $i$.

The acceleration matrix can be defined as the sum of the time derivative of the velocity plus the velocity squared

$H_{i,j(k)}={\dot {W}}_{i,j(k)}+W_{i,j(k)}^{2}$

The velocity and the acceleration in frame $i$ of a point of body $j$ can be evaluated as

${\dot {P}}=W_{i,j}P$

${\ddot {P}}=H_{i,j}P$

It is also possible to prove that

${\dot {M}}_{i,j}=W_{i,j(i)}M_{i,j}$

${\ddot {M}}_{i,j}=H_{i,j(i)}M_{i,j}$

Velocity and acceleration matrices add up according to the following rules

$W_{i,k}=W_{i,j}+W_{j,k}$

$H_{i,k}=H_{i,j}+H_{j,k}+2W_{i,j}W_{j,k}$

in other words the absolute velocity is the sum of the parent velocity plus the relative velocity; for the acceleration the Coriolis' term is also present.

The components of velocity and acceleration matrices are expressed in an arbitrary frame $k$ and transform from one frame to another by the following rule

$W_{(h)}=M_{h,k}W_{(k)}M_{k,h}$

$H_{(h)}=M_{h,k}H_{(k)}M_{k,h}$

Jacobian Matrix (Portions Copied from Link, Link, and Link)

The time derivative of the kinematics equations yields the Jacobian of the robot, which relates the joint rates to the linear and angular velocity of the end-effector. The principle of virtual work shows that the Jacobian also provides a relationship between joint torques and the resultant force and torque applied by the end-effector. Singular configurations of the robot are identified by studying its Jacobian.

Velocity kinematics

The robot Jacobian results in a set of linear equations that relate the joint rates to the six-vector formed from the angular and linear velocity of the end-effector, known as a twist. Specifying the joint rates yields the end-effector twist directly.

Twists

A popular, and minimal way to represent the time derivative of a pose is a twist. A twist consists of two 3 × 1 vectors: $\omega$ and $v$, where $\omega$ is the angular velocity of the moving rigid body (manipulator link), and $v$ is the linear velocity of the point on the moving rigid body that instantaneously coincides with the origin of the reference frame.

$t={\begin{bmatrix}{\begin{array}{c}\omega \\v\end{array}}\end{bmatrix}}$

Propagation of Velocity

Rotational velocities that are written with respect to the same frame can simply be added. Hence:

$_{i+1}\omega _{i+1}=\,_{i+1}^{i}R\,_{i}\omega _{i}+{\begin{bmatrix}0\\0\\{\dot {\theta }}_{i+1}\end{bmatrix}}$

The linear velocity of the origin of a link is that of the origin of the preceding link plus a rotational component:

$_{i+1}v_{i+1}=\,_{i+1}^{i}R\left(_{i}v_{i}+_{i}\omega _{i}\times \,_{i}P_{i+1}\right)$

Note: In the above equations the resulting velocities are expressed relative to the frame of the current link. $_{i}P_{i+1}$ is the vector pointing from the origin of frame ${i}$ to that of frame ${i+1}$.

Example: The Two-Link Planar Manipulator

The two-link planar manipulator.

The link transformations that come with this manipulator can be easily derived graphically from looking at the figure on the right:

$_{0}^{1}T={\begin{bmatrix}c_{1}&-s_{1}&0&0\\s_{1}&c_{1}&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}$

$_{1}^{2}T={\begin{bmatrix}c_{2}&-s_{2}&0&l_{1}\\s_{2}&c_{2}&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}$

$_{2}^{3}T={\begin{bmatrix}1&0&0&l_{2}\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}$

Here, $l_{1}$ and $l_{2}$ are the lengths link 1 and 2, respectively.

Note: Notice again the use of $s_{i}$ and $c_{i}$ as shorthand notations for $sin(\theta _{i})$ and $cos(\theta _{i})$, respectively.

Hence, from the above equations:

$_{2}\omega _{2}={\begin{bmatrix}0\\0\\{\dot {\theta _{1}}}+{\dot {\theta _{2}}}\end{bmatrix}}$

and:

$_{3}\omega _{3}=_{2}\omega _{2}$

Also:

$_{2}v_{2}={\begin{bmatrix}c_{2}&s_{2}&0\\-s_{2}&c_{2}&0\\0&0&1\end{bmatrix}}\left[{\begin{bmatrix}0\\0\\{\dot {\theta _{1}}}\end{bmatrix}}\times {\begin{bmatrix}l_{1}\\0\\0\end{bmatrix}}\right]={\begin{bmatrix}l_{1}s_{2}{\dot {\theta _{1}}}\\l_{1}c_{2}{\dot {\theta _{1}}}\\0\end{bmatrix}}$

and:

$_{3}v_{3}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}\left[{\begin{bmatrix}l_{1}s_{2}{\dot {\theta _{1}}}\\l_{1}c_{2}{\dot {\theta _{1}}}\\0\end{bmatrix}}+{\begin{bmatrix}0\\0\\{\dot {\theta _{1}}}+{\dot {\theta _{2}}}\end{bmatrix}}\times {\begin{bmatrix}l_{2}\\0\\0\end{bmatrix}}\right]={\begin{bmatrix}l_{1}s_{2}{\dot {\theta _{1}}}\\l_{1}c_{2}{\dot {\theta _{1}}}+l_{2}({\dot {\theta _{1}}}+{\dot {\theta _{2}}})\\0\end{bmatrix}}$

With respect to the base frame, the end-effector velocity becomes:

$_{0}v_{3}=\,_{0}^{3}R\,_{3}v_{3}=\,_{0}^{1}R\,_{1}^{2}R\,_{2}^{3}R\,_{3}v_{3}={\begin{bmatrix}-l_{1}s_{1}{\dot {\theta _{1}}}-l_{2}s_{12}({\dot {\theta _{1}}}+{\dot {\theta _{2}}})\\l_{1}c_{1}{\dot {\theta _{1}}}+l_{2}c_{12}({\dot {\theta _{1}}}+{\dot {\theta _{2}}})\\0\end{bmatrix}}$

Code

%reset -f
import numpy as np
import sympy as sp

theta1, theta2 = sp.symbols('theta1 theta2')
l1, l2 = sp.symbols('l1 l2')
theta1dot, theta2dot = sp.symbols('theta1dot theta2dot')

f1_f0_T=np.array([[sp.cos(theta1), -sp.sin(theta1), 0, 0],
             [sp.sin(theta1), sp.cos(theta1), 0, 0],
             [0, 0, 1, 0],
             [0, 0, 1, 0]])
f2_f1_T=np.array([[sp.cos(theta2), -sp.sin(theta2), 0, l1],
            [sp.sin(theta2), sp.cos(theta2),0, 0],
            [0, 0, 1, 0],
            [0, 0, 1, 0]])

f3_f2_T=np.array([[1, 0, 0, l2],
            [0, 1, 0, 0],
            [0, 0, 1, 0],
            [0, 0, 0, 1]])

#Extract rotation matrices from homogeneous transforms
f1_f0_R=np.delete(f1_f0_T,3,axis=0)
f1_f0_R=np.delete(f1_f0_R,3,axis=1)

f2_f1_R=np.delete(f2_f1_T,3,axis=0)
f2_f1_R=np.delete(f2_f1_R,3,axis=1)

f3_f2_R=np.delete(f3_f2_T,3,axis=0)
f3_f2_R=np.delete(f3_f2_R,3,axis=1)

f1_P_2=np.transpose(np.array([[f2_f1_T[0][3],f2_f1_T[1][3],f2_f1_T[2][3]]]))
f2_P_3=np.transpose(np.array([[f3_f2_T[0][3],f3_f2_T[1][3],f3_f2_T[2][3]]]))


f1_omega_1=np.array([[0,0,theta1dot]])
f1_omega_1=f1_omega_1.T

f0_f1_R=f1_f0_R.T
f1_f2_R=f2_f1_R.T
f2_f3_R=f3_f2_R.T

#Calculate f2_omega_2
f2_omega_2=np.dot(f1_f2_R,f1_omega_1)+np.transpose(np.array([[0,0,theta2dot]]))
print("f2_omega_2:\n", f2_omega_2)

#Calculate f3_omega_3
f3_omega_3=np.dot(f2_f3_R,f2_omega_2)+np.transpose(np.array([[0,0,0]]))
print("f3_omega_3:\n", f3_omega_3)

#Calculate f1_v_1
f1_v_1=np.transpose(np.array([[0,0,0]]))

#Calculate f2_v_2
#Note: Taking the cross product of two column vectors requires taking the transpose of
#the cross of the transposed column vectors
f2_v_2=np.dot(f1_f2_R,(f1_v_1+np.transpose(np.cross(f1_omega_1.T,f1_P_2.T))))
print("f2_v_2:\n",f2_v_2)

#Calculate f3_v_3
f3_v_3=np.dot(f2_f3_R,(f2_v_2+np.transpose(np.cross(f2_omega_2.T,f2_P_3.T))))
f3_v_3=sp.simplify(f3_v_3)
print("f3_v_3:\n",f3_v_3)

#Calculate f0_v_3
f0_v_3=np.dot(f1_f0_R,np.dot(f2_f1_R,np.dot(f3_f2_R,f3_v_3)))
f0_v_3=sp.simplify(f0_v_3)
print("f0_v_3:\n",f0_v_3)

Jacobian

Suppose $m$ kinematic (end-effector) equations. Each is a function of $n$ degrees of freedom:

${\begin{array}{ccc}x_{1}&=&x_{1}(\theta _{1},\ldots ,\theta _{n})\\\vdots &&\vdots \\x_{m}&=&x_{m}(\theta _{1},\ldots ,\theta _{n})\\\end{array}}$

Note that in the case of a non-redundant manipulator, $m=n$.

The time derivate of the above equations is found as follows:

${\begin{array}{ccc}{\dfrac {dx_{1}}{dt}}&=&{\dfrac {\partial x_{1}}{\partial \theta _{1}}}{\dfrac {d\theta _{1}}{dt}}+\cdots +{\dfrac {\partial x_{1}}{\partial \theta _{n}}}{\dfrac {d\theta _{n}}{dt}}\\\vdots &&\vdots \\{\dfrac {dx_{m}}{dt}}&=&{\dfrac {\partial x_{m}}{\partial \theta _{1}}}{\dfrac {d\theta _{1}}{dt}}+\cdots +{\dfrac {\partial x_{m}}{\partial \theta _{n}}}{\dfrac {d\theta _{n}}{dt}}\end{array}}$

This can be written in vector form:

$v=J{\frac {d\theta }{dt}}$

The matrix $J$ is called the Jacobian, the matrix of which the elements are the partial derivatives of the kinematics equations. The relationship between the end-effector velocity and the (known) joint velocities is thus fully described by the Jacobian. The end-effector velocity is a linear function of the joint velocities.

$J={\begin{bmatrix}{\frac {\partial x_{1}}{\partial \theta _{1}}}&\cdots &{\frac {\partial x_{1}}{\partial \theta _{n}}}\\\vdots &\ddots &\vdots \\{\frac {\partial x_{m}}{\partial \theta _{1}}}&\cdots &{\frac {\partial x_{m}}{\partial \theta _{n}}}\end{bmatrix}}$

Example: The Two-Link Planar Manipulator

This example presents a slightly other way of solving the above problem. The position kinematics equations of this manipulator can be easily derived using the technique presented in the Serial Manipulator Position Kinematics section, or graphically from looking at the figure above:

${\begin{array}{l}x=l_{1}\cos(\theta _{1})+l_{2}\cos(\theta _{1}+\theta _{2})\\y=l_{1}\sin(\theta _{1})+l_{2}\sin(\theta _{1}+\theta _{2})\end{array}}$

Here, the Jacobian is:

$J={\begin{bmatrix}-l_{1}\sin(\theta _{1})-l_{2}\sin(\theta _{1}+\theta _{2})&-l_{2}\sin(\theta _{1}+\theta _{2})\\l_{1}\cos(\theta _{1})+l_{2}\cos(\theta _{1}+\theta _{2})&l_{2}\cos(\theta _{1}+\theta _{2})\\\end{bmatrix}}$

Hence, the end-effector velocity is:

${\begin{array}{ccc}{\dfrac {dx}{dt}}&=&\left[-l_{1}\sin(\theta _{1})-l_{2}\sin(\theta _{1}+\theta _{2})\right]{\dfrac {d\theta _{1}}{dt}}-l_{2}\sin(\theta _{1}+\theta _{2}){\dfrac {d\theta _{2}}{dt}}\\{\dfrac {dy}{dt}}&=&\left[l_{1}\cos(\theta _{1})+l_{2}\cos(\theta _{1}+\theta _{2})\right]{\dfrac {d\theta _{1}}{dt}}+l_{2}\cos(\theta _{1}+\theta _{2}){\dfrac {d\theta _{2}}{dt}}\\\end{array}}$

Note that the end-effector's angular velocity is, of course, the sum of the joint velocities. Another possibility that yields exactly the same result would be to explicitly include the equation for angular velocity and then calculate the Jacobian accordingly. This result is, as could already be expected, the same as the one in the above example, where the link transformation matrices were used to achieve the result.

Code

%reset -f
import numpy as np
import sympy as sp

theta1, theta2 = sp.symbols('theta1 theta2')
l1, l2 = sp.symbols('l1 l2')

f1_f0_T=np.array([[sp.cos(theta1), -sp.sin(theta1), 0, 0],
             [sp.sin(theta1), sp.cos(theta1), 0, 0],
             [0, 0, 1, 0],
             [0, 0, 0, 1]])

f2_f1_T=np.array([[sp.cos(theta2), -sp.sin(theta2), 0, l1],
            [sp.sin(theta2), sp.cos(theta2),0, 0],
            [0, 0, 1, 0],
            [0, 0, 0, 1]])

f3_f2_T=np.array([[1, 0, 0, l2],
            [0, 1, 0, 0],
            [0, 0, 1, 0],
            [0, 0, 0, 1]])

End_Coord=np.transpose(np.array([[0,0,0,1]]))
X=np.dot(f1_f0_T,np.dot(f2_f1_T,np.dot(f3_f2_T,End_Coord)))
X=sp.simplify(X)
print("X:\n",X)

J=np.array([[sp.diff(X[0],theta1),sp.diff(X[0],theta2)],
           [sp.diff(X[1],theta1),sp.diff(X[1],theta2)]])
print("J:\n",J)

theta1dot, theta2dot = sp.symbols('theta1dot theta2dot')
thetadot=np.transpose(np.array([[theta1dot, theta2dot]]))

f0_v_3=np.dot(J,thetadot)
print("f0_v_3:\n",f0_v_3)

Additional Examples for Jacobian Matrices in Robotics

Additional Examples for Jacobian Matrices for Robotics