Physics equations/Sheet/Astronomy
Appearance
Astronomy dimensions
[edit | edit source]- Earth's Radius: R⊕ ≈ 6.37x106m
- Earth's Mass: M⊕ ≈ 5.97×1024kg
- Solar and Lunar radius and mass:
- Solar radius and mass: R☉≈110R⊕ and M☉ ≈ 330,000M⊕.
- Lunar radius and mass: RL ≈ 0.273R⊕ and ML ≈ 0.0123M⊕
- Earth-moon distance ≈ 60R⊕
- Earth-Sun distance = 1AU ≈ 1.496x1011m ≈ 23481R⊕
- One light-year ≈ 9.5×1015 m = 63240 AU
- One parsec ≈ 3.26 light-years
Kepler-Newton Mass,Period,Distance (normalized units)
[edit | edit source]- , where P is the period of orbit in years, and a is the semi-major axis measured in AU. The net mass, , is the sum of the mass of both bodies, and is normalized to the mass of the Sun. For a planet of mass, , orbiting a star of much larger mass, , the normalized net mass is . The mass of the Sun, , is 1.99×1030 kilograms. If for some object, then that object is twice as massive as the Sun. One year is 3.15×107 seconds.
Parallax
[edit | edit source]- , where D is the distance to the object in parsecs, θ is the parallax angle in arcseconds, and b is the baseline in AU; b=1 for observations taken from Earth. One degree is 60 arcminutes and one arcminute is 60 arseconds. One AU ≈ 1.5x1011 meters, and one parsec ≈ 3.26 light-years, and one light-year ≈ 9.5×1015 meters.
Inverse square
[edit | edit source]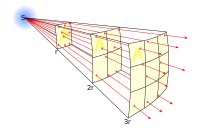
- is a "normalized intensity", closely related to relative magnitude, that allows students to combine equations and solve problems without resorting to the logarithmic magnitude scale. If the distance to the stellar object, D, is measured in parsecs, it is the power per square parsec that enters a telescope on Earth. The luminosity, , (in solar units) is a measure of the absolute magnitude. In general, is the inverse-square law.
Photons, waves, and particles
[edit | edit source]
- is the energy of a photon, where f is frequency and h ≈6.6×10-34m2kg/s is Plank's constant, and c ≈3×108m/s is the speed of light. Also, E=ℏ ω where ℏ ≈1.05×10m2kg/s and ω =2π f.
- relates frequency, wavelength, and the speed (or phase velocity). Using wavenumber, k =2π/λ, this can also be represented as ω =ck.
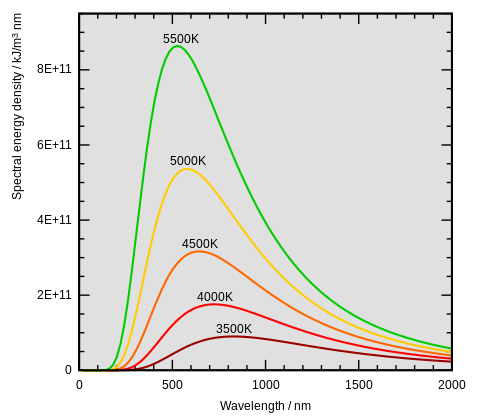
Blackbody radiation
[edit | edit source]

- is Wein's law that relates the peak emission wavelength, λmax, of a black body to temperature, T measured in Kelvins. Peak wavelength, λmax, is measured in nanometers (1nm=10-9m). If temperature is measured in units normalized to the Sun's temperature, , then
- where is the temperature normalized to the Sun's temperature.
The Stefan-Boltzmann law is usually written as P=σAT4, where A is surface area, T is temperature (in Kelvins), and σ is the Stefan-Boltzmann constant. The power, P, can be written as normalized luminosity, , where L☉ =3.85×1026W is the power output (or luminosity) of the Sun. In these normalized units, the Stefan-Boltzmann law is:
- , where is the radius and temperature normalized to the Sun's radius and is the temperature normalized to the Sun's temperature.