Physics equations/Relative Velocity

Relative velocity in one dimension

Relative motion man on train

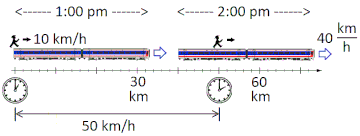
We begin with relative motion in the classical, (or non-relativistic, or the Newtonian approximation) that all speeds are much less than the speed of light. This limit is associated with the w:Galilean transformation. The figure shows a man on top of a train, at the back edge. At 1:00 pm he begins to walk forward at a walking speed of 10 km/hr (kilometers per hour). The train is moving at 40 km/hr. The figure depicts the man and train at two different times: first, when the journey began, and also one hour later at 2:00 pm. The figure suggests that the man is 50 km from the starting point after having traveled (by walking and by train) for one hour. This, by definition, is 50 km/hour, which suggests that the prescription for calculating relative velocity in this fashion is to add the two velocities.

The figure displays clocks and rulers to remind the reader that while the logic behind this calculation seem flawless, it makes false assumptions about how clocks and rulers behave. (See The train-and-platform thought experiment.) To recognize that this classical model of relative motion violates w:special relativity, we generalize the example into an equation:

$\underbrace {{\vec {v}}_{M|E}} _{50\;km/hr}=\underbrace {{\vec {v}}_{M|T}} _{10\;km/hr}+\underbrace {{\vec {v}}_{T|E}} _{40\;km/hr}\,,$

where:

${\vec {v}}_{M|E}$ is the velocity of the Man relative to Earth.

${\vec {v}}_{M|T}$ is the velocity of the Man relative to the Train.

${\vec {v}}_{T|E}$ is the velocity of the Train relative to Earth.

Fully legitimate expressions for "the velocity of A relative to B" include "the velocity of A with respect to B" and "the velocity of A in the coordinate system where B is always at rest". The violation of special relativity occurs because this equation for relative velocity falsely predicts that different observers will measure different speeds when observing the motion of light.

Relative velocity in two dimensions

Vector addition (A+B=C) and subtraction (B=C-A)

A displacement is a 'step' or jump from one place to the other. It can be represented as an arrow (vector) with the convention that the tail represents the initial location, and the head (arrow) represents the final destination.

Let $(\ell _{A},\ell _{B},\ell _{C})$ represent the lengths of the three vectors shown in the figure. In the language of vector algebra, $\ell _{A}=|{\vec {A}}|\,...)$, where the arrow above denotes that the entity has both magnitude and direction (i.e., is a vector). The figure caption shows an alternative notation in which vectors are bold faced. It is also common to write the length (called magnitude) by the same letter without bold face or arrow: A=|A|, or $A=|{\vec {A}}|,$.

Suppose two objects, A and C, begin at the same place at time $t_{0}=0$, and each arrives at its destination (at the head of the vector) at time, $t$. Later in the course we will learn about vector addition and subtraction. Just for giggles, lets state the previous equation in the new variables and see what happens. Here "Earth" is the stationary point where both objects began their journeys:

In a problem like this, it is helpful to change variables. If A is the train and C is the man we have $T\rightarrow A\quad M\rightarrow C$. We also multiply by $\Delta t$. After changing the subscripts the above equation looks like:

$\underbrace {{\vec {v}}_{C|E}\Delta t} _{\vec {C}}=\underbrace {{\vec {v}}_{C|A}\Delta t} _{\vec {B}}+\underbrace {{\vec {v}}_{A|E}\Delta t} _{\vec {A}}\,,$.

where:

${\vec {v}}_{C|E}$ is the velocity of the C relative to Earth.

${\vec {v}}_{C|A}$ is the velocity of the C relative to the A.

${\vec {v}}_{A|E}$ is the velocity of the C relative to Earth.

You should have arrived at this equation through 'mindless' substitution of one variable for the other from the linear train equation. Now look at the figure and convince yourself that this is correct vector addition.

Relativistic Motion

Now let the bullet and the gun be relativistic.

$v_{O'|O}$ is the speed of the train w.r.t. Earth.

$v_{A|O'}$ is the speed of the bullet w.r.t. the train.

$v_{A|O}$ is the speed of the bullet w.r.t. Earth.

Define u=v/c where c = 2.998x10⁸m/s is the speed of light. The relativistic velocity addition formula is:

$u_{A|O}={\frac {u_{A|O'}+u_{O'|O}}{1+(u_{A|O\,'})(u_{O\,'|O})}}$

Example: Consider the case where $v_{O'|O}=v_{A|O'}=.9c$. The non-relativistic formula would have predicted:

$v_{A|O}=.9c+.9c=1.8c$

Instead, the relativistic formula predicts:

$v_{A|O}={\frac {1.8}{1.81}}c<c$

It is also easy to verify that:

$v_{A|O}=c$ if either $v_{O'|O}=c$ or $v_{A|O'}=c$

In other words, if something is going at the speed of light, then all observers will measure it to be going at the same speed, which is known as the 'speed of light', c.

Faster-than-light signals are impossible

It is generally agreed that no object and no information can travel faster than light. Suppose you had a telephone that sends signals along a wire at a speed that exceeds that of light. You could put that wire on a train and send a signal to the past. Oddly, it is necessary to have the train go in the opposite direction to which the message is being sent. Arrange for the train to be traveling in the negative direction, at a speed of $v_{T|O}=-.9c$. Let the Message replace the 'man' in the figure that begins this section, and let $v_{M|T}=+1.1c$. This is how fast the message is moving in the train's reference frame. (The train is where this hypothetical faster-than-light telephone is situated.) To calculate the speed of this message in your (Earth) reference frame:

$v_{M|E}={\frac {(-.9)+(1.1)}{1+(-.9)(1.1)}}c=-20c$

Curiously, this message seems to be traveling in the wrong direction. A detailed analysis shows that the speed of the Message relative to Earth is negative because:

$v_{M|E}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}<0$, where

$x_{f}-x_{i}>0$ because the message is being sent to a person to the right.

$t_{f}-i_{i}<0$ because the message is received before it was sent.

A pair of such superluminal telephones mounted on subluminal trains traveling in opposite directions could be used to send a message to your own past. Wikipedia refers to this as the grandfather paradox, since the boss of a crime syndicate could order the murder of his own grandfather. This might be possible if there are an infinite number of parallel universes, so that the universe with the murdered grandfather would never contain the crime syndicate boss.

But it is simpler to assume that superluminal communication is impossible (Occam's razor).

Having said that, this issue of superluminal speeds does arise within the context of physics and is orten referred to as the issue of causality. One example is Bell's theorem (See Bell’s Theorem and Psychic Phenomena). In this case, the prospect of superluminal communication is not claimed. Instead it is used to demonstrate how surprising Bell's theorem is. Also, it is possible to observe objects in deep space that appear to be traveling faster than light, but in reality they are not (see superluminal motion. Occasionally a scientist or group will claim that something important is observed to travel faster than the speed of light. But historically such speculative claims have always been proven false. (See faster-than-light)