Physics equations/Paraxial approximation

The paraxial approximation

from https://en.wikipedia.org/w/index.php?title=Lens_(optics)&oldid=581829952

The paraxial approximation can be used to derive simple equations involving lenses. A statement of the approximation involves the optical axis, which is a line that passes through the center of each lens and is oriented in a direction normal to the surface of the lens (at the center). The paraxial approximation approximation is valid for rays that make a small angle to the optical axis of the system, and also lie close to the optical axis, throughout the system.

Thin lens approximation

Further simplification occurs when we assume that the lenses are sufficiently thin; this is known as the thin lens approximation. In this approximation, two points, called focal points, are situated at equal lengths to the left and right of the lens. Focal points are denoted with the capital letter F, while the distance from the focal point to the center of a then lens is called the focal length, denoted by the lower case f.

Warning: The point where all the ray coming from a given point on an object is called the image, which is generally not the same as the focal point of a lens.

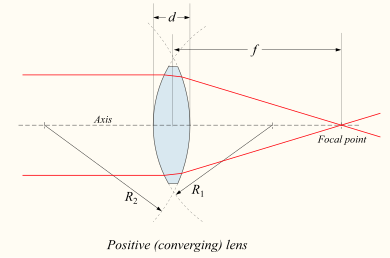
Focal length of a converging (positive) lens

If a lens is converging, or positive, a collimated beam of light passing through the lens will converged to a point behind the lens. The distance from the lens to the spot is the focal length of the lens, which is commonly abbreviated f in diagrams and equations. By convention, f is always positive for a converging lens. The plane perpendicular to the lens axis situated at a distance f from the lens is called the focal plane.

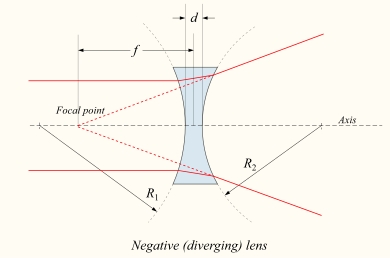
Focal length of a diverging (negative) lens

If a lens is diverging, or negative, a collimated| beam of light passing through the lens will diverge after passing through the lens. As they diverge, they appear to be emanating from a particular point on the axis in front of the lens. The the distance from this point to the lens is also known as the focal length. By convention, f is always negative for a diverging lens. , although it is negative with respect to the focal length of a converging lens.

Object and image distance

Real image by a converging lens. By the sign convention, *(S₁, S₂, f)* are all represented by positive values.

The detailed prediction of how images are produced by these lenses can be made using either ray-tracing methods or equations. Thin lenses follow a simple equation that determines the location of the images given a particular focal length ( $f$ ) and object distance ( $S_{1}$ ):

{\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}={\frac {1}{f}}

where $S_{2}$ is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens. The focal length f is considered negative for concave lenses.

Real image for converging lens occurs when S₁ > f >0

It is customary with lenses to assume that the light travels from left to right, and in such cases, the convention is that the object distance S_1 is positive. If the lens is converging, f>0, and if S₁>f, the equation above yields a value of S₂ that is positive, which means that the image is to the right of the lens. Such an image is called a real image, because rays actually converge to that point.

Virtual image for converging lens occurs when S₁>0 < f

By the sign convention, S₁ and f are positive, while S₂ is negative.

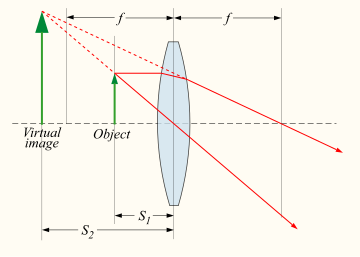
If the object is moved closer to the lens than it's own focal length, the equations predict that S₂ < 0. In this case the image is on the left of the lens. In other words, the rays on the right side of the lens are diverging as if they originated at a point to the left of the lens. Such an image is called a virtual image. When a magnifying glass is used in this way, it is impossible to converge all the light from a source to a single point. This situation does describe the use of a magnifying glass or reading glasses to better see something that is small and/or too close to the eye for comfortable viewing.

Image at infinity occurs for converging lens occurs if S₁ = f > 0

If S₁ = f , then our equation (1/S₁ + 1/S₂ = 1/f) yields what may seem like the meaningless result, S₂ = 1/0. This is a good place to mention that "infinity" has a practical value. Consider the mathematical statement:

{\frac {1}{0}}=\pm \infty

We can give meaning to this equation, by realizing that in practice one cannot put the image exactly at a given point, with 0% error. If "0" is a very small positive number, then 1/"0" is very large and positive. If "0" is very close to zero, but negative, then 1/"0" approaches negative infinity. It is customary to use superscripts to indicate the sign of a number that is approaching zero: 0^- is negative and 0⁺ is positive. Physically, the two infinities (positive and negative) are also "nearly equal" in that both represent nearly parallel rays that either slightly diverge or slightly converge.

Virtual images from a diverging lens

The formulas above may also be used for negative (diverging) lens by using a negative focal length (f), but for these lenses only virtual images can be formed.

magnification

The magnification of the lens is ratio of image to object height, and is therefore given by:

M=-{\frac {S_{2}}{S_{1}}}

,

where M is the magnification factor; if |M|>1, the image is larger than the object. Notice the sign convention here shows that, if M is negative, as it is for real images, the image is upside-down with respect to the object. For virtual images, M is positive and the image is upright.

Quiz