Physics equations/Oscillations, waves, and interference
Simple harmonic motion
[edit | edit source]Simple harmonic motion occurs when the restoring force is directly proportional to the displacement. It can serve to model many physical systems. Hooke's law states that the restoring force F of a spring obeys, , where k is the spring constant, and x is the displacement from the equilibrium position.
Since a=d2x/dt2, the equation of motion becomes a linear second order differential equation:
where we define as a (constant) parameter in the ordinary differential equation.
The general solution can be described in a variety of ways; all have exactly two arbitrary constants of motion that arise from the fact that the initial position and initial velocity must be determined in order to model the system:
where is the the angular frequency; ωT = 2π and fT= 1 are useful for relating angular frequency, frequency, and period. Horizontal motion of a pendulum is one of many examples of a system that approximately obeys simple harmonic motion, with ω2 = g/L, where L is the length of the pendulum. The velocity and acceleration as a function of time are:
Energy of simple harmonic motion
[edit | edit source]The kinetic energy K of the system at time t is
and the potential energy is
The total mechanical energy of the system therefore has the constant value
A simple travelling wave
[edit | edit source]from

Although ψ (psi) is often associated with quantum theory, Lord Rayleigh used that symbol describe sound waves. An idealized model of transverse waves on a stretched string assumes that the string propagates a signal of any shape, without distortion, in either direction.[1] The height of the wave is:
The two functions and represent two arbitrary wave forms travelling in opposite directions. For example, if , the wave has the shape, , and this shape travels to the right at velocity, . It can be shown that this wave obeys the partial differential equation:
- (where is a constant).
Travelling wave solutions to this wave equation can take on many forms; a simple but important solution is:
where (A, B, φA, φB } are arbitrary constants. A and B are called amplitudes, while (φA, φB) are phases. Another pair of constants is k and ω (wavenumber and angular frequency); they are constrained by |ω/k| = v0, which is called the phase speed. The relation between ω and is called the dispersion relation. This dispersion relation has two branches, ω(k)=±v0k. Other dispersion relations exist. For example bending waves on a long thin rod have a dispersion with four branches (not all real numbers ): ω2=v0k4.
Beats and group velocity
[edit | edit source]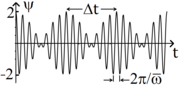
For example, consider two closely space frequencies, and :
- and (so that ).
It can be shown that for a wave with a sinusoidal time dependence:
- where is the envelope.
A 'wavetrain' is the infinite sequence of wavepackets that occurs when two 'plane waves' of equal amplitude are added. A true isolated wavepacket requires an infinite number waves the form cos(kx-ωt) but with a little algebra, one can discern a great deal by studying wavetrains. If the envelope, A(t), varies so slowly over time that it is essentially constant over many oscillations of the higher frequency. Defining Δt as the time between consecutive zeros of the envelope:
The corresponding result for a wavetrain that varies with x is also shown, as there is a one-to-one correspondence between ω and k in these equations. More rigorous definitions of Δω and Δk lead to Heisenberg's uncertainty principles, (Δω)(Δt) ≥1/2 and(Δk (Δx)≥ 1/2. In this formalism, wavepackets move with the group velocity, dx/dt=∂ω/∂k. Strict plane waves, such as cos(kx-ωt), typically occur only if the medium is homogeneous (in time and space). But if the inhomogeniety is sufficiently gentle (see eikonal approximation), then we have another equation of motion: dk/dt=-∂ω/∂x. In this approximation, wavepackets move exactly as do Newtonian particles.
The Algebra: The trigonometry is often more transparent if we use Euler's equation and take the real part, taking to be the real part of .
Using well-known properties of exponents:
It is left as an exercise to the reader to perform this calculation for a travelling wave
A simple standing wave
[edit | edit source]
The second derivative in Newton's second law of motion usually implies that two initial conditions (position and velocity) are necessary and sufficient to establish future motion. With waves it is necessary to establish these initial conditions for each of the infinitely many points along a string. For example, in the previous solutions to the wave equation, there are an infinite number of values that the angular frequency might take. We illustrate this with transverse waves on a string of length L, with both ends of the string held clamped. The general solution for this system can be written as,
where are arbitrary constants and each angular frequency obeys the dispersion relation, . (For a string of linear mass density μ, the wave speed obeys v2 = T/μ, where T is the tension in the string.) can often be used to find the arbitrary constants. Fourier analysis can be used to find the arbitrary constants, provided the initial conditions are known.
Fourier Series Example:' Suppose the initial conditions at are:
- and
(where f(x) is a known function), then:
Using Fourier analysis, it can be shown that:






































