Physics equations/Impulse, momentum, and motion about a fixed axis

Impulse and momentum

Impulse is denoted by the symbols I (which is too easily confused with moment of inertia), or Imp, or J (we shall use the latter):

${\vec {J}}=F\Delta t\rightarrow \int _{t_{1}}^{t_{2}}{\vec {F}}(t)dt$

Momentum (or linear momentum) is:

${\vec {p}}=m{\vec {v}}\rightarrow m_{1}{\vec {v_{1}}}+m_{2}{\vec {v_{2}}}\rightarrow \sum m_{j}{\vec {v_{j}}}$

Total linear momentum is an extrinsic and conserved quantity, provided the net external force is zero. It can be shown that momentum obeys (d/dt)Σp=ΣF_ext. Kinetic energy and momentum are related by,K=½mv²=p²/(2m). Linear momentum is related to linear momentum by the impulse-momentum theorem:

${\vec {J}}={\vec {p_{2}}}-{\vec {p_{1}}}=\Delta {\vec {p}}$

- click to hide or see derivation -

From Newton's second law, force is related to momentum p by

$\mathbf {F} ={\frac {d\mathbf {p} }{dt}}.$. Therefore,

${\begin{aligned}\mathbf {J} &=\int _{t_{1}}^{t_{2}}{\frac {d\mathbf {p} }{dt}}\,dt\\&=\int _{p_{1}}^{p_{2}}d\mathbf {p} \\&=\mathbf {p_{2}} -\mathbf {p_{1}} =\Delta \mathbf {p} ,\end{aligned}}$

where Δp is the change in linear momentum from time t₁ to t₂. This is often called the impulse-momentum theorem.

Torque

A particle is located at position r relative to its axis of rotation. When a force F is applied to the particle, only the perpendicular component F_⊥ produces a torque. This torque τ = r × F has magnitude τ = |r| |F_⊥| = |r| |F| sinθ and is directed outward from the page.

Showing three formulas for torque

Torque, moment or moment of force is also called moment. The symbol for torque is typically τ, the Greek letter tau. When it is called moment, it is commonly denoted M. The SI units for torque is the newton metre (N·m). It would be inadvisable to call this a Joule, even though a Joule is also a (N·m).

More generally, the torque on a particle (which has the position r in some reference frame) can be defined as the cross product:

${\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} ,$

where r is the particle's position vector relative to the fulcrum, and F is the force acting on the particle. The magnitude τ of the torque is given by

$\tau =rF\sin \theta ,\!$

where r is the distance from the axis of rotation to the particle, F is the magnitude of the force applied, and θ is the angle between the position and force vectors. Alternatively,

$\tau =rF_{\perp }=r_{\perp }F,$

where F_⊥ is the amount of force directed perpendicularly to the position of the particle and r_⊥ is called the lever arm.

Rotational motion about a fixed axis

Rotation of a rigid object P about a fixed object about a fixed axis O.

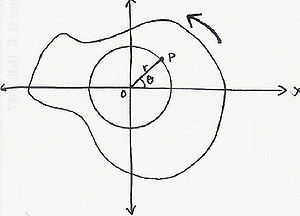
Angular displacement may be measured in radians or degrees. If using radians, it provides a very simple relationship between distance traveled around the circle and the distance r from the center.

A particle moves in a circle of radius $r$. Having moved an arc length $s$, its angular position is $\theta$ relative to its original position, where $\theta ={\frac {s}{r}}$.

In mathematics and physics it is usual to use the natural unit radians rather than degrees or revolutions. Units are converted as follows:

$1\mathrm {\ rev} =360^{\circ }=2\pi \mathrm {\ rad}$

An angular displacement is described as

$\Delta \theta =\theta _{2}-\theta _{1},\!$

Angular speed and angular velocity

Angular velocity is the change in angular displacement per unit time. The symbol for angular velocity is $\omega$ and the units are typically rad s⁻¹. Angular speed is the magnitude of angular velocity.

${\overline {\omega }}={\frac {\Delta \theta }{\Delta t}}={\frac {\theta _{2}-\theta _{1}}{t_{2}-t_{1}}}.$

The instantaneous angular velocity is related to particles speed by

$\omega (t)={\frac {d\theta }{dt}}={\frac {v}{r}},$

where $v$ is the transitional speed of the particle. A changing angular velocity indicates the presence of an angular acceleration in rigid body, typically measured in rad s⁻². The average angular acceleration ${\overline {\alpha }}$ over a time interval Δt is given by

${\overline {\alpha }}={\frac {\Delta \omega }{\Delta t}}={\frac {\omega _{2}-\omega _{1}}{t_{2}-t_{1}}}.$

The instantaneous acceleration α(t) is given by

$\alpha (t)={\frac {d\omega }{dt}}={\frac {d^{2}\theta }{dt^{2}}}={\frac {a}{r}}.$

Kinematic equations of motion

When the angular acceleration is constant, the five quantities angular displacement $\theta$, initial angular velocity $\omega _{i}$, final angular velocity $\omega _{f}$, angular acceleration $\alpha$, and time $t$ can be related by four equations of kinematics:

$\omega _{f}=\omega _{i}+\alpha t\;\!$

$\theta =\omega _{i}t+{\begin{matrix}{\frac {1}{2}}\end{matrix}}\alpha t^{2}$

$\omega _{f}^{2}=\omega _{i}^{2}+2\alpha \theta$

$\theta ={\tfrac {1}{2}}\left(\omega _{f}+\omega _{i}\right)t$

Kinetic energy

This 1906 rotary shear uses the moment of inertia of two flywheels to store kinetic energy which when released is used to cut metal stock (International Library of Technology, 1906).

The kinetic energy of a rigid system of particles moving in the plane is given by

$K=\sum _{i=1}^{N}{\frac {1}{2}}\,m_{i}\mathbf {v} _{i}\cdot \mathbf {v} _{i}=\sum _{i=1}^{N}{\frac {1}{2}}\,m_{i}(\omega r_{i})^{2}={\frac {1}{2}}\,\omega ^{2}\sum _{i=1}^{N}m_{i}r_{i}^{2}.$

Thus, $K=I\omega ^{2}$ where $I=\sum _{i=1}^{N}m_{i}r_{i}^{2}.$ is called the moment of inertia.

The moment of inertia of a continuous body rotating about a specified axis is calculated in the same way, with the summation replaced by the integral,

$I=\int _{V}\rho (\mathbf {r} )\,\mathbf {r} ^{2}\,dV\rightarrow \int _{S}\sigma (\mathbf {r} )\,\mathbf {r} ^{2}\,dS\rightarrow \int _{\ell }\lambda (x)x^{2}\,d\ell$

Here r is the distance to the axis and ρ=ρ(r) is the mass density. As shown above, this can be converted into a line, surface, or volume integral for a substance with a surface mass density ρ(x,y) or line mass density λ(x)

Torque, angular momentum, and work

The rotational equivalent of Newton's ,F = ma, linear momentum as, p = mv, and work as W = FΔx → ʃFdx, is $\tau =I\alpha$ , $L=I\omega$ , and $W=\tau \Delta \theta$, respectively.Here, L is angular momentum, which does not have the same units as linear momentum. But work, W, is measured in the same units (Joules).

Moments of inertia for simple geometries (hidden table)

- click to hide or see table-

Description	Figure	Moment(s) of inertia
Point mass m at a distance r from the axis of rotation.		$I=mr^{2}$
Two point masses, M and m, with reduced mass $\mu$ and separated by a distance, x.		$I={\frac {Mm}{M\!+\!m}}x^{2}=\mu x^{2}$
Rod of length L and mass m (Axis of rotation at the end of the rod)		$I_{\mathrm {end} }={\frac {mL^{2}}{3}}\,\!$
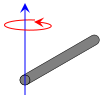
Rod of length L and mass m		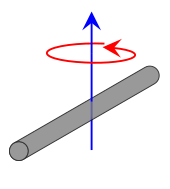$I_{\mathrm {center} }={\frac {mL^{2}}{12}}\,\!$
Thin circular hoop of radius r and mass m		$I_{z}=mr^{2}\!$ $I_{x}=I_{y}={\frac {mr^{2}}{2}}\,\!$
Thin cylindrical shell with open ends, of radius r and mass m		$I=mr^{2}\,\!$
Solid cylinder of radius r, height h and mass m		$I_{z}={\frac {mr^{2}}{2}}\,\!$ $I_{x}=I_{y}={\frac {1}{12}}m\left(3r^{2}+h^{2}\right)$
Sphere (hollow) of radius r and mass m		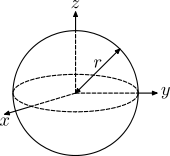$I={\frac {2mr^{2}}{3}}\,\!$
Ball (solid) of radius r and mass m		$I={\frac {2mr^{2}}{5}}\,\!$
Thin rectangular plate of height h and of width w and mass m (Axis of rotation at the end of the plate)		$I_{e}={\frac {mh^{2}}{3}}+{\frac {mw^{2}}{12}}\,\!$
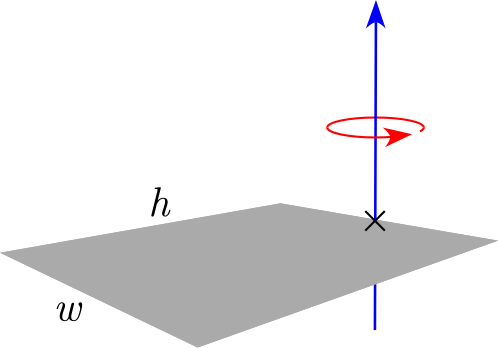
Solid cuboid of height h, width w, and depth d, and mass m		$I_{h}={\frac {1}{12}}m\left(w^{2}+d^{2}\right)$ $I_{w}={\frac {1}{12}}m\left(h^{2}+d^{2}\right)$ $I_{d}={\frac {1}{12}}m\left(h^{2}+w^{2}\right)$

references are hidden