Physics equations/Fluids

Pressure and bulk modulus

Mass density is the ratio,$\rho =m/V$ where $m$ is mass and $V$ is volume. Pressure is force per unit area $P=F/A$ The SI unit of pressure is the pascal (1 Pa =N/m² ). The the bar is defined as 100 kPa, and the atmosphere (atm) is approximately 101.325 kPA = 14.7 lb/in^{^2}. If a substance changes by increases by a small amount $\Delta P$, one would expect the volume to decrease by a small amount $\Delta V$. An intrinsic parameter is a parameter that depends only on the intrinsic properties of the substance, and not on the amount of matter present. Since $\Delta V/V$ and $\Delta P$ are both intrinsic variables, so is the ratio, $B$, which is called the bulk modulus:

$B=-{\frac {\Delta P}{\Delta V/V}}$

Pressure versus Depth

Pressure is the weight per unit area of the fluid above a point.

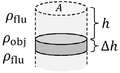
The pressure at a depth, $h$ below the surface of a stationary fluid can be found by adding the weight (per area) of the fluid above to the pressure at the top surface. Using the volume of the cylinder (see figure) to calculate this weight (mg = ρghA), we obtain:

$P=P_{0}+\rho gh$

where $P_{0}$ is (atmospheric) the pressure at the top surface, $h$ is the depth, and $\rho$ is the mass density of the fluid. In many cases, only the difference between two pressures appears in the final answer to a question, and in such cases it is permissible to set the pressure at the top surface of the fluid equal to zero. When $P_{0}$ is artificially set equal to zero in this way, the resulting pressure, $P_{gauge}=\rho gh$, is called the gauge pressure. Gauge pressure is also used to describe the deviation from atmospheric pressure in laboratory experiments involving a confined gas. Pressure in a stationary fluid depends only on depth even if the shape is not cylindrical. This is known as Pascal's Principle.

Buoyancy and Archimedes' principle

Pascal's principle does not hold if two fluids are separated by a seal that prohibits fluid flow (as in the case of the piston of an internal combustion engine). Suppose the upper and lower fluids shown in the figure are not sealed, so that a fluid of mass density $\rho _{flu}$ comes to equilibrium above and below an object. Let the object have a mass density of $\rho _{obj}$ and a volume of $A\Delta h$, as shown in the figure. The net (bottom minus top) force on the object due to the fluid is called the buoyant force:

${\rm {{buoyant}\;{\rm {{force}=(A\Delta h)(\rho _{flu})g\,}}}}$,

and is directed upward. The volume in this formula, AΔh, is called the volume of the displaced fluid, since placing the volume into a fluid at that location requires the removal of that amount of fluid. Archimedes principle states:

A body wholly or partially submerged in a fluid is buoyed up by a force equal to the weight of the displaced fluid.

Note that if $\rho _{obj}=\rho _{flu}$, the buoyant force exactly cancels the force of gravity. A fluid element within a stationary fluid will remain stationary. But if the two densities are not equal, a third force (in addition to weight and the buoyant force) is required to hold the object at that depth. If an object is floating or partially submerged, the volume of the displaced fluid equals the volume of that portion of the object which is below the waterline.

figures

Continuity Equation for Incompressible Fluids

A fluid element speeds up if the area is constricted.

Consider a pipe with cross-sectional area $A$ that varies along the pipe. If the variation is sufficiently smooth, the volume of pipe is $\Delta V=A\Delta x$ along a distance $\Delta x$. If this volume passes a point along the pipe in a time interval $\Delta t$, then the the speed of the fluid is $v=\Delta x/\Delta t$. Since the fluid is incompressible, the volume flow rate, $\left(\Delta V/\Delta t\right)_{in}$, into one end of the pipe equals the volume flow rate exiting the other end, $\left(\Delta V/\Delta t\right)_{in}$. In other words, for an incompressible fluid:

$A_{1}v_{1}=A_{2}v_{2}\rightarrow \oint {\vec {v}}\cdot {\hat {n}}dA=0\rightarrow \nabla \cdot {\vec {v}}=0\;({\rm {{for}\;{\rm {{incompressible}\;{\rm {{fluids})}}}}}}$

In the ultra powerful notation, ${\hat {n}}$ is the outward unit vector, and the integral is over the entire surface, including the sides of the pipe as well as both ends. The final result uses methods introduced at the end of this book.)

The Bernoulli Equation

Bernoulli's equation holds for any incompressible fluid when fluid viscosity can be neglected it is valid along any streamline of the fluid.

$P_{1}+\rho gh_{1}+{\frac {1}{2}}\rho v_{1}^{2}=P_{2}+\rho gh_{2}+{\frac {1}{2}}\rho v_{2}^{2}$