GeoGebra/Perspective Drawing on Mirror
This article can be used as Wiki2Reveal presentation to explain the geometrical workflow of creating a perspective drawing on a mirror. You annotate the slides in the browser by pressing the button [C]. With [F] you can show the slides in fullscreen mode. The slides are fetched from Wikiversity. Improve slides directly in Wikiversity. Improvements are visible on reload of Wiki2Reveal slides.
Introduction
[edit | edit source]This learning resource is about perpective drawing of 3D objects on a mirror and learn about geometric principles of construction. Together with this learning resource a GitHub repository with Geogebra Files[1] was created that can be opened with dynamic geometry software Geogebra. The construction is based on a german article in the journal Mathematica Didactica 26 (2003) Bd.1 43, Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Engelbert Niehaus[2]. You can download the Geogebra files as ZIP from the GitHub repository[3].
Learning Tasks
[edit | edit source]The tasks are divided into the following areas.
- Theoretical background
- Geogebra construction
- Projection of circles
- Projection of a sine curve
Theoretical background
[edit | edit source]Analyze the theoretical background[2] for perspective drawing[4], in which the non-digital environment is a mirror used as a projection surface on which, for example, the perspective image is drawn with a foil pen.
Vanishing Point Perspective
[edit | edit source]The Vanishing point perspective is a way of perspective drawing.
Perspective Drawing in Art
[edit | edit source]Geogebra construction
[edit | edit source]Starting from this situation of drawing objects in perspective on a mirror, we will now discuss constructions in Geogebra:
- Z construction for the projection of half-lines,
- X construction for the projection of points as the intersection of two half-lines. Here, the image point is generated via two Z constructions.
- I construction for the projection of a perpendicular line generated via two X constructions.
Projection of circles
[edit | edit source]Consider how to use a locus line and an X construction to create the projective image of a circle.
Projection from a sine curve
[edit | edit source]Consider how to use a locus line and an X construction to create the projective image of a sine curve in the standing plane. First, draw the graph of the figure:
for appropriate parameters . Use sliders for these parameters. Use the X-construction to the create perspective projection of a single point on the graph of
3D Construction of Projections in Geogebra
[edit | edit source]The repository contains Geogebra files for learning 3D projections on a mirror Z-, X, and I-construction of 3D point and lines. This repository has additional learning material for the Open Source software Geogebra and the file are bundled in a GitHub repositopry[1] created for this Wikiversity Learning Resource about Perspective Drawing. Keep in mind that line through the point Z in the upper paper plane of the 3D world provides the correponding vanishing point directly by the intersection with the horizon h. Parallel lines in the 3D world have the same vanishing point on the horzion. This geometric property leads to the Z-construction to find the corresponding vanishing point for half lines in the ground plane.
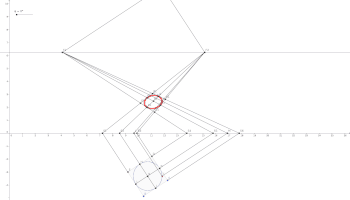
Basic Situation in Front of a Mirror
[edit | edit source]The following image shows the basic situation of a 3D projection on a mirror. The perspective image of the box is painted on the mirror.
Use a Paper as Mediator between 3D and 2D Construction
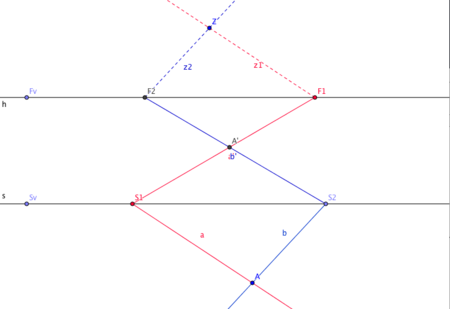
[edit | edit source]You can use a paper as mediator between the 3D world and the 2D projection on the paper. The point Z is the point where the eye is located. h is the horizon of the contruction and s is parallel to the horizon h as the intersection of the groundplane and plane of the mirror. Projected objects "stand" on the groundplane and the projection to the mirror plane is the objective of the construction.
Basic Geometry in Front of the Mirror
[edit | edit source]The perspective drawing creates an image of an object in front of a mirror. The eye observes the projective image from a point Z. We assume that the observer is painting the perspective image of a vertical line/stick on the surface of the mirror with pen. Considering the perspective construction from the side will lead to the following situation.
Z-Construction for Lines on a Surface
[edit | edit source]We unfold the paper mediator between 2D and 3D construction and transfer the folding to two parallel lines in Geogebra.
A Z-construction generates perspective image of a half-line b with ground line s. The intersection with the ground line is the point S1. Assume you want to draw the projective image of the half line b on the mirror plane. To create the projective image you need the following steps.
- draw a parallel line
dto the half linebthrough the point of the eyeZ. The intersection of that linedwith the horizon generates the vanishing pointF2for the projection of the halflinebto the mirror plane. - The line between
F1andS1is the projective image of the half-lineb.
X-Construction for Point on a Surface
[edit | edit source]The X-construction creates the perspective image of a point by using 2 Z-constructions.
I-Construction for a Vertical Line
[edit | edit source]The I-construction creates the perspective image of vertical line segment by using 2 X-constructions.
3D-Object generated with Z-,X- and I-Construction
[edit | edit source]Stereoscopy
[edit | edit source]Spatial perception is required to interact with your environment and relevant for geometric and spatial learning objectives (e.g. in chemistry[5]. The constructions mentioned above can be extended to Stereoscopy.
Learning Activity - Projection of Circle
[edit | edit source]Use trigonometric functions to move a point on a circle with a slider. Use the X-construction to create the corresponding projected point and move the a slider between the value in the plane of the stand on circular path.
Animation for the Projection of Circles
[edit | edit source]The following GIF animation shows the projection of a circle with a slider for the angle and application of the X-construction to generate the perspective trace of the projected point of the given circle in the plane of stand.
Learning Activities - Stereoscopy
[edit | edit source]
- Analyze the stereoscopic image for spatial differences in the projective mapping for the left and right eye.
- Describe the applications of Stereoscopy and history when the first applications Stereoscopy were used.
Animation - Distance of Eyes
[edit | edit source]The following animation shows the difference of the projections according to the position of left eye and right eye .
External Resources
[edit | edit source]- GitHub Resources with Geogebra Files as ZIP-File
- GitHub Repository for Wikiversity Learning Resource
- Orthogonal Projection in Schools with Geogebra - by Anna Hundertmark
See also
[edit | edit source]- 3D Modelling
- Projective Geometry
- Regard3D
- Photogrammetry
- Perspective Drawing
- Equirectangular projection
- Stereoscopy
References
[edit | edit source]- ↑ 1.0 1.1 3D Construction with Geogebra (2017-2019) Engelbert Niehaus, URL: https://github.com/niebert/3D_Construction_Geogebra (accessed 2019/06/12)
- ↑ 2.0 2.1 Niehaus, Engelbert (2003), Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Mathematica Didactica 26 (2003) Bd.1 43, http://www.mathematica-didactica.com/altejahrgaenge/md_2003/md_2003_1_Niehaus_Spiegelung.pdf
- ↑ Gegeobra Files as ZIP - 3D Construction (2017-19) URL: https://github.com/niebert/3D_Construction_Geogebra/archive/master.zip - (accessed 2020/11/27)
- ↑ D'amelio, J. (2004). Perspective drawing handbook. Courier Corporation.
- ↑ Coleman, S. L., & Gotch, A. J. (1998). Spatial perception skills of chemistry students. Journal of Chemical Education, 75(2), 206.
Page Information
[edit | edit source]You can display this page as Wiki2Reveal slides
Wiki2Reveal
[edit | edit source]The Wiki2Reveal slides were created for the GeoGebra' and the Link for the Wiki2Reveal Slides was created with the link generator.
- This page is designed as a PanDocElectron-SLIDE document type.
- Source: Wikiversity https://en.wikiversity.org/wiki/GeoGebra/Perspective%20Drawing%20on%20Mirror
- see Wiki2Reveal for the functionality of Wiki2Reveal.











![{\displaystyle t\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbc9ed8510c75442ce1d2e73f021258fc7e04c6)