Template:EduV/announcement
Equations lifted from chapter summaries in https://cnx.org/contents/1Q9uMg_a@9.7:Gofkr9Oy@10/Preface
Introduction
metric prefixes
da
h
k
M
G
T
P
E
Z
Y
deca
hecto
kilo
mega
giga
tera
peta
exa
zetta
yotta
1E+01
1E+02
1E+03
1E+06
1E+09
1E+12
1E+15
1E+18
1E+21
1E+24
d
c
m
µ
n
p
f
a
z
y
deci
centi
milli
micro
nano
pico
femto
atto
zepto
yocto
1E-01
1E-02
1E-03
1E-06
1E-09
1E-12
1E-15
1E-18
1E-21
1E-24
The base SI units are mass: kg (kilogram); length: m (meter); time: s (second). Percent error is
(
δ
A
/
A
)
×
100
%
{\displaystyle (\delta A/A)\times 100\%}
▭ If
A
→
+
B
→
=
C
→
{\displaystyle {\vec {A}}+{\vec {B}}={\vec {C}}}
x +Bx =Cx , etc , and vector subtraction is defined by
B
→
=
C
→
−
A
→
{\displaystyle {\vec {B}}={\vec {C}}-{\vec {A}}}
▭ The two-dimensional displacement from the origin is
r
→
=
x
i
^
+
y
j
^
{\displaystyle {\vec {r}}=x{\hat {i}}+y{\hat {j}}}
magnitude is
A
≡
|
A
→
|
=
A
x
2
+
A
y
2
{\displaystyle A\equiv |{\vec {A}}|={\sqrt {A_{x}^{2}+A_{y}^{2}}}}
angle (phase ) is
θ
=
tan
−
1
(
y
/
x
)
{\displaystyle \theta =\tan ^{-1}{(y/x)}}
▭ Scalar multiplication
α
A
→
=
α
A
x
i
^
+
α
A
y
j
^
+
.
.
.
{\displaystyle \alpha {\vec {A}}=\alpha A_{x}{\hat {i}}+\alpha A_{y}{\hat {j}}+...\quad }
▭ Any vector divided by its magnitude is a unit vector and has unit magnitude:
|
V
^
|
=
1
{\displaystyle |{\hat {V}}|=1}
V
^
≡
V
→
/
V
{\displaystyle {\hat {V}}\equiv {\vec {V}}/V}
▭ Dot product
A
→
⋅
B
→
=
A
B
cos
θ
=
A
x
B
x
+
A
y
B
y
+
.
.
.
{\displaystyle {\vec {A}}\cdot {\vec {B}}=AB\cos \theta =A_{x}B_{x}+A_{y}B_{y}+...\quad }
A
→
⋅
A
→
=
A
2
{\displaystyle {\vec {A}}\cdot {\vec {A}}=A^{2}}
▭ Cross product
A
→
=
B
→
×
C
→
⇒
{\displaystyle {\vec {A}}={\vec {B}}\times {\vec {C}}\Rightarrow }
A
α
=
B
β
C
γ
−
C
γ
A
β
{\displaystyle A_{\alpha }=B_{\beta }C_{\gamma }-C_{\gamma }A_{\beta }}
(
α
,
β
,
γ
)
{\displaystyle (\alpha ,\beta ,\gamma )}
cyclic permutation of
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
▭ Cross-product magnitudes obey
A
=
B
C
sin
θ
{\displaystyle A=BC\sin \theta }
θ
{\displaystyle \theta }
B
→
{\displaystyle {\vec {B}}}
C
→
{\displaystyle {\vec {C}}}
A
→
⊥
{
B
→
,
C
→
}
{\displaystyle {\vec {A}}\perp \{{\vec {B}},{\vec {C}}\}}
right hand rule .
▭ Vector identities
c
(
A
+
B
)
=
c
A
+
c
B
{\displaystyle \;c(\mathbf {A} +\mathbf {B} )=c\mathbf {A} +c\mathbf {B} \quad }
▭
A
+
B
=
B
+
A
{\displaystyle \mathbf {A} +\mathbf {B} =\mathbf {B} +\mathbf {A} \quad }
▭
A
+
(
B
+
C
)
=
(
A
+
B
)
+
C
{\displaystyle \mathbf {A} +(\mathbf {B} +\mathbf {C} )=(\mathbf {A} +\mathbf {B} )+\mathbf {C} \quad }
▭
A
⋅
B
=
B
⋅
A
{\displaystyle \mathbf {A} \cdot \mathbf {B} =\mathbf {B} \cdot \mathbf {A} \quad }
▭
A
×
B
=
−
B
×
A
{\displaystyle \mathbf {A} \times \mathbf {B} =\mathbf {-B} \times \mathbf {A} \quad }
▭
(
A
+
B
)
⋅
C
=
A
⋅
C
+
B
⋅
C
{\displaystyle \left(\mathbf {A} +\mathbf {B} \right)\cdot \mathbf {C} =\mathbf {A} \cdot \mathbf {C} +\mathbf {B} \cdot \mathbf {C} \quad }
▭
(
A
+
B
)
×
C
=
A
×
C
+
B
×
C
{\displaystyle \left(\mathbf {A} +\mathbf {B} \right)\times \mathbf {C} =\mathbf {A} \times \mathbf {C} +\mathbf {B} \times \mathbf {C} \quad }
▭
A
⋅
(
B
×
C
)
=
B
⋅
(
C
×
A
)
=
(
A
×
B
)
⋅
C
{\displaystyle \mathbf {A} \cdot \left(\mathbf {B} \times \mathbf {C} \right)=\mathbf {B} \cdot \left(\mathbf {C} \times \mathbf {A} \right)=\left(\mathbf {A} \times \mathbf {B} \right)\cdot \mathbf {C} \quad }
▭
A
×
(
B
×
C
)
=
(
A
⋅
C
)
B
−
(
A
⋅
B
)
C
{\displaystyle \mathbf {A\times } \left(\mathbf {B} \times \mathbf {C} \right)=\left(\mathbf {A} \cdot \mathbf {C} \right)\mathbf {B} -\left(\mathbf {A} \cdot \mathbf {B} \right)\mathbf {C} \quad }
▭
(
A
×
B
)
⋅
(
C
×
D
)
=
(
A
⋅
C
)
(
B
⋅
D
)
−
(
B
⋅
C
)
(
A
⋅
D
)
{\displaystyle \mathbf {\left(A\times B\right)\cdot } \left(\mathbf {C} \times \mathbf {D} \right)=\left(\mathbf {A} \cdot \mathbf {C} \right)\left(\mathbf {B} \cdot \mathbf {D} \right)-\left(\mathbf {B} \cdot \mathbf {C} \right)\left(\mathbf {A} \cdot \mathbf {D} \right)}
Delta as difference
Δ
x
=
x
f
−
x
i
→
d
x
→
0
{\displaystyle \Delta x=x_{f}-x_{i}\rightarrow dx\rightarrow 0}
▭ Average velocity
v
¯
=
Δ
x
/
Δ
t
→
v
=
d
x
/
d
t
{\displaystyle {\bar {v}}=\Delta x/\Delta t\rightarrow v=dx/dt}
▭ Acceleration
a
¯
=
Δ
v
/
Δ
t
→
a
=
d
v
/
d
t
{\displaystyle {\bar {a}}=\Delta v/\Delta t\rightarrow a=dv/dt}
▭ WLOG set
Δ
t
=
t
{\displaystyle \Delta t=t\;}
Δ
x
=
x
−
x
0
{\displaystyle \Delta x=x-x_{0}\;}
t
i
=
0
{\displaystyle t_{i}=0}
Δ
v
=
v
−
v
0
{\displaystyle \Delta v=v-v_{0}}
v
(
t
)
=
∫
0
t
a
(
t
′
)
d
t
′
+
v
0
{\displaystyle \;v(t)=\int _{0}^{t}a(t')dt'+v_{0}}
x
(
t
)
=
∫
0
t
v
(
t
′
)
d
t
′
+
x
0
=
x
0
+
v
¯
t
{\displaystyle \;x(t)=\int _{0}^{t}v(t')dt'+x_{0}=x_{0}+{\bar {v}}t}
v
¯
=
1
t
∫
0
t
v
(
t
′
)
d
t
′
{\displaystyle {\bar {v}}={\frac {1}{t}}\int _{0}^{t}v(t')dt'}
average velocity .
▭ At constant acceleration:
v
¯
=
v
0
+
v
2
,
v
=
v
0
+
a
t
,
x
=
x
0
+
v
0
t
+
1
2
a
t
2
,
{\displaystyle {\bar {v}}={\tfrac {v_{0}+v}{2}},\quad v=v_{0}+at,\quad x=x_{0}+v_{0}t+{\tfrac {1}{2}}at^{2},\,}
v
2
=
v
0
2
+
2
a
Δ
x
{\displaystyle v^{2}=v_{0}^{2}+2a\Delta x}
▭ For free fall , replace
x
→
y
{\displaystyle x\rightarrow y}
a
→
−
g
{\displaystyle a\rightarrow -g}
g
{\displaystyle g}
2 at Earth's surface ).
▭ Acceleration
a
→
=
a
x
i
^
+
a
y
j
^
+
a
z
k
^
{\displaystyle {\vec {a}}=a_{x}{\hat {i}}+a_{y}{\hat {j}}+a_{z}{\hat {k}}}
a
x
(
t
)
=
d
v
x
/
d
t
=
d
2
x
/
d
t
2
{\displaystyle a_{x}(t)=dv_{x}/dt=d^{2}x/dt^{2}}
▭ Average values :
v
→
a
v
e
=
Δ
r
→
Δ
t
=
r
→
(
t
2
)
−
r
→
(
t
2
)
t
2
−
t
1
{\displaystyle {\vec {v}}_{ave}={\tfrac {\Delta {\vec {r}}}{\Delta t}}={\tfrac {{\vec {r}}(t_{2})-{\vec {r}}(t_{2})}{t_{2}-t_{1}}}}
a
→
a
v
e
=
Δ
v
→
Δ
t
=
v
→
(
t
2
)
−
v
→
(
t
2
)
t
2
−
t
1
{\displaystyle \;{\vec {a}}_{ave}={\tfrac {\Delta {\vec {v}}}{\Delta t}}={\tfrac {{\vec {v}}(t_{2})-{\vec {v}}(t_{2})}{t_{2}-t_{1}}}}
▭ Free fall time of flight
T
o
f
=
2
(
v
0
sin
θ
0
)
g
,
{\displaystyle \,T_{of}={\tfrac {2(v_{0}\sin \theta _{0})}{g}}\,,\,}
Trajectory
y
=
(
tan
θ
0
)
x
−
[
g
2
(
v
0
cos
θ
0
)
2
]
x
2
,
{\displaystyle y=(\tan \theta _{0})x-\left[{\tfrac {g}{2(v_{0}\cos \theta _{0})^{2}}}\right]x^{2}\,,\,}
Range
R
=
v
0
2
sin
2
θ
0
g
{\displaystyle R={\tfrac {v_{0}^{2}\sin 2\theta _{0}}{g}}}
▭ Uniform circular motion :
|
a
→
|
=
a
C
=
ω
2
r
=
v
2
/
r
{\displaystyle |{\vec {a}}|=a_{C}=\omega ^{2}r=v^{2}/r}
v
≡
|
v
→
|
=
ω
r
{\displaystyle v\equiv |{\vec {v}}|=\omega r}
r
→
=
A
cos
ω
t
i
^
+
A
sin
ω
t
j
^
,
{\displaystyle {\vec {r}}=A\cos \omega t{\hat {i}}+A\sin \omega t{\hat {j}}\,,\,}
v
→
=
−
A
ω
sin
ω
t
i
^
+
A
ω
cos
ω
t
j
^
,
{\displaystyle {\vec {v}}=-A\omega \sin \omega t{\hat {i}}+A\omega \cos \omega t{\hat {j}}\,,\,}
a
→
=
−
A
ω
2
cos
ω
t
i
^
−
A
ω
2
sin
ω
t
j
^
.
{\displaystyle {\vec {a}}=-A\omega ^{2}\cos \omega t{\hat {i}}-A\omega ^{2}\sin \omega t{\hat {j}}\,.}
Tangential and centripetal acceleration
a
→
=
a
→
c
+
a
→
T
{\displaystyle {\vec {a}}={\vec {a}}_{c}+{\vec {a}}_{T}}
a
T
=
d
|
v
→
|
/
d
t
{\displaystyle a_{T}=d|{\vec {v}}|/dt}
▭ Relative motion :
r
→
P
S
=
r
→
P
S
′
+
r
→
S
′
S
{\displaystyle \,{\vec {r}}_{PS}={\vec {r}}_{PS'}+{\vec {r}}_{S'S}}
v
→
P
S
=
v
→
P
S
′
+
v
→
S
′
S
{\displaystyle \,{\vec {v}}_{PS}={\vec {v}}_{PS'}+{\vec {v}}_{S'S}}
v
→
P
C
=
v
→
P
A
+
v
→
A
B
+
v
→
B
C
{\displaystyle \,{\vec {v}}_{PC}={\vec {v}}_{PA}+{\vec {v}}_{AB}+{\vec {v}}_{BC}}
a
→
P
S
=
a
→
P
S
′
+
a
→
S
′
S
{\displaystyle \,{\vec {a}}_{PS}={\vec {a}}_{PS'}+{\vec {a}}_{S'S}}
▭ Weight
=
w
→
=
m
g
→
{\displaystyle ={\vec {w}}=m{\vec {g}}}
▭ normal force is a component of the contact force by the surface. If the only forces are contact and weight,
|
N
→
|
=
N
=
m
g
cos
θ
{\displaystyle |{\vec {N}}|=N=mg\cos \theta }
θ
{\displaystyle \theta }
incline .
▭ Hooke's law
F
=
−
k
x
{\displaystyle F=-kx}
k
{\displaystyle k}
▭ Centripetal force
F
c
=
m
v
2
/
r
=
m
r
ω
2
{\displaystyle F_{c}=mv^{2}/r=mr\omega ^{2}}
uniform circular motion . Angular velocity
ω
{\displaystyle \omega }
radians per second.
▭ Ideal angle of banked curve :
tan
θ
=
v
2
/
(
r
g
)
{\displaystyle \tan \theta =v^{2}/(rg)}
r
{\displaystyle r}
θ
{\displaystyle \theta }
▭ Drag equation
F
D
=
1
2
C
ρ
A
v
2
{\displaystyle F_{D}={\tfrac {1}{2}}C\rho Av^{2}}
C
=
{\displaystyle C=}
Drag coefficient ,
ρ
=
{\displaystyle \rho =}
mass density ,
A
=
{\displaystyle A=}
v
=
{\displaystyle v=}
Holds approximately for large Reynold's number
=
R
e
=
ρ
v
L
/
η
{\displaystyle =\mathrm {Re} =\rho vL/\eta }
η
=
{\displaystyle \eta =}
dynamic viscosity ;
L
=
{\displaystyle L=}
▭ Stokes's law models a sphere of radius
r
{\displaystyle r}
F
s
=
6
π
r
η
v
{\displaystyle F_{s}=6\pi r\eta v}
Infinitesimal work done by force:
d
W
=
F
→
⋅
d
r
→
=
|
F
→
|
|
d
r
→
|
cos
θ
{\displaystyle dW={\vec {F}}\cdot d{\vec {r}}=|{\vec {F}}|\,|d{\vec {r}}|\cos \theta }
path integral
W
A
B
=
∫
A
B
F
→
⋅
d
r
→
{\displaystyle W_{AB}=\int _{A}^{B}{\vec {F}}\cdot d{\vec {r}}}
▭ Work done from A→B by friction
−
f
k
|
ℓ
A
B
|
,
{\displaystyle -f_{k}|\ell _{AB}|,\;}
−
m
g
(
y
B
−
y
A
)
,
{\displaystyle -mg(y_{B}-y_{A}),\;}
spring
−
1
2
k
(
x
B
2
−
x
A
2
)
{\displaystyle -{\tfrac {1}{2}}k\left(x_{B}^{2}-x_{A}^{2}\right)}
▭ Work-energy theorem : The work done on a particle is
W
n
e
t
=
K
B
−
K
A
{\displaystyle W_{net}=K_{B}-K_{A}}
kinetic energy
=
K
=
1
2
m
v
2
=
p
2
2
m
{\displaystyle =K={\tfrac {1}{2}}mv^{2}={\frac {p^{2}}{2m}}}
▭ Power
=
P
=
d
W
/
d
t
=
F
→
⋅
v
→
{\displaystyle =P=dW/dt={\vec {F}}\cdot {\vec {v}}}
U
=
m
g
y
+
C
{\displaystyle U=mgy+{\mathcal {C}}}
gravitational PE Earth's surface .
U
=
1
2
k
x
2
+
C
{\displaystyle U={\tfrac {1}{2}}kx^{2}+{\mathcal {C}}}
spring )
▭ Conservative force :
∮
F
→
cons
⋅
d
r
→
=
0
{\displaystyle \oint {\vec {F}}_{\text{cons}}\cdot d{\vec {r}}=0}
2D ,
F
→
(
x
,
y
)
{\displaystyle {\vec {F}}(x,y)}
if and only if
F
→
=
−
(
∂
U
/
∂
x
)
i
^
−
(
∂
U
/
∂
y
)
j
^
⟺
∂
F
x
/
∂
y
=
∂
F
y
/
∂
x
{\displaystyle {\vec {F}}=-(\partial U/\partial x)\,{\hat {i}}-(\partial U/\partial y)\,{\hat {j}}\iff \partial F_{x}/\partial y=\partial F_{y}/\partial x}
▭ Mechanical energy is conserved if no non-conservative forces are present:
0
=
W
n
c
,
A
B
=
Δ
(
K
+
U
)
A
B
=
Δ
E
A
B
{\displaystyle 0=W_{nc,AB}=\Delta (K+U)_{AB}=\Delta E_{AB}}
F
→
(
t
)
=
d
p
→
/
d
t
, where
p
→
=
m
v
→
{\displaystyle {\vec {F}}(t)=d{\vec {p}}/dt{\text{, where }}{\vec {p}}=m{\vec {v}}}
momentum .
▭ Impulse-momentum theorem
J
→
=
F
a
v
e
Δ
t
=
∫
t
i
t
f
F
→
d
t
=
Δ
p
→
{\displaystyle {\vec {J}}=F_{ave}\Delta t=\int _{t_{i}}^{t_{f}}{\vec {F}}dt=\Delta {\vec {p}}}
▭ For 2 particles in 2D
If
F
→
e
x
t
=
0
then
∑
j
=
1
N
p
→
j
=
0
⇒
p
f
,
α
=
p
1
,
i
,
α
+
p
2
,
i
,
α
{\displaystyle {\text{If }}{\vec {F}}_{ext}=0{\text{ then }}\sum _{j=1}^{N}{\vec {p}}_{j}=0\Rightarrow p_{f,\alpha }=p_{1,i,\alpha }+p_{2,i,\alpha }}
▭ Center of mass :
r
→
C
M
=
1
M
∑
j
=
1
N
m
j
r
→
j
→
1
M
∫
r
→
d
m
,
{\displaystyle {\vec {r}}_{CM}={\tfrac {1}{M}}\sum _{j=1}^{N}m_{j}{\vec {r}}_{j}\rightarrow {\tfrac {1}{M}}\int {\vec {r}}dm,}
v
→
C
M
=
d
d
t
r
→
C
M
{\displaystyle {\vec {v}}_{CM}={\tfrac {\,d}{dt}}{\vec {r}}_{CM}}
p
→
C
M
=
∑
j
=
1
N
m
j
v
→
j
=
M
v
→
C
M
.
{\displaystyle {\vec {p}}_{CM}=\sum _{j=1}^{N}m_{j}{\vec {v}}_{j}=M{\vec {v}}_{CM}.}
▭
F
→
=
d
d
t
p
→
C
M
=
m
a
→
C
M
=
∑
j
=
1
N
m
j
a
→
j
{\displaystyle {\vec {F}}={\tfrac {\,d}{dt}}{\vec {p}}_{CM}=m{\vec {a}}_{CM}=\sum _{j=1}^{N}m_{j}{\vec {a}}_{j}}
▭ Rocket equation
m
d
v
=
−
u
d
m
⇒
Δ
v
=
u
ln
(
m
f
/
m
i
)
{\displaystyle mdv=-udm\Rightarrow \Delta v=u\ln(m_{f}/m_{i})}
WRT the rocket.
▭
v
t
=
ω
r
=
d
s
/
d
t
{\displaystyle \,v_{t}=\omega r=ds/dt\,}
tangential speed . Angular acceleration is
α
=
d
ω
/
d
t
=
d
2
θ
/
d
t
2
{\displaystyle \alpha =d\omega /dt=d^{2}\theta /dt^{2}\,}
a
t
=
α
r
=
d
2
s
/
d
t
2
{\displaystyle a_{t}=\alpha r=d^{2}s/dt^{2}\,}
▭ Constant angular acceleration
ω
¯
=
1
2
(
ω
0
+
ω
f
)
{\displaystyle {\bar {\omega }}={\tfrac {1}{2}}(\omega _{0}+\omega _{f})\,}
▭
θ
f
=
θ
0
+
ω
¯
t
=
θ
0
+
ω
0
t
+
1
2
α
t
2
.
{\displaystyle \theta _{f}=\theta _{0}+{\bar {\omega }}t=\theta _{0}+\omega _{0}t+{\tfrac {1}{2}}\alpha t^{2}\,.}
▭
ω
f
=
ω
0
+
α
t
.
{\displaystyle \omega _{f}=\omega _{0}+\alpha t.\,}
ω
f
2
=
ω
0
2
+
2
α
Δ
θ
.
{\displaystyle \omega _{f}^{2}=\omega _{0}^{2}+2\alpha \Delta \theta \,.}
▭ Total acceleration is centripetal plus tangential :
a
→
=
a
→
c
+
a
→
t
.
{\displaystyle {\vec {a}}={\vec {a}}_{c}+{\vec {a}}_{t}.\,}
▭ Rotational kinetic energy is
K
=
1
2
I
ω
2
,
{\displaystyle K={\tfrac {1}{2}}I\omega ^{2},\,}
I
=
∑
j
m
j
r
j
2
→
∫
r
2
d
m
{\displaystyle I=\sum _{j}m_{j}r_{j}^{2}\rightarrow \int r^{2}dm}
Moment of inertia .
▭ parallel axis theorem
I
p
a
r
a
l
l
e
l
−
a
x
i
s
=
I
c
e
n
t
e
r
o
f
m
a
s
s
+
m
d
2
{\displaystyle I_{parallel-axis}=I_{center\,of\,mass}+md^{2}}
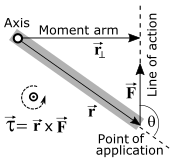
▭ Restricting ourselves to fixed axis rotation ,
r
{\displaystyle r}
torques ,
τ
→
=
r
→
×
F
→
{\displaystyle {\vec {\tau }}={\vec {r}}\times {\vec {F}}}
τ
n
e
t
=
∑
τ
j
=
∑
r
⊥
j
F
j
=
I
α
{\displaystyle \tau _{net}=\sum \tau _{j}=\sum r_{\perp _{j}}F_{j}=I\alpha }
▭ Work done by a torque is
d
W
=
(
∑
τ
j
)
d
θ
{\displaystyle dW=\left(\sum \tau _{j}\right)d\theta }
Work-energy theorem is
K
B
−
K
A
=
W
A
B
=
∫
θ
A
θ
B
(
∑
j
τ
j
)
d
θ
{\displaystyle K_{B}-K_{A}=W_{AB}=\int _{\theta _{A}}^{\theta _{B}}\left(\sum _{j}\tau _{j}\right)d\theta }
▭ Rotational power
=
P
=
τ
ω
{\displaystyle =P=\tau \omega }
I=∫r2 dm for a hoop, disk, cylinder, box, plate, rod, and spherical shell or solid can be found
▭ Total angular momentum and net torque :
d
L
→
/
d
t
=
∑
τ
→
{\displaystyle d{\vec {L}}/dt=\sum {\vec {\tau }}}
=
l
→
1
+
l
→
2
+
.
.
.
;
{\displaystyle ={\vec {l}}_{1}+{\vec {l}}_{2}+...;}
l
→
=
r
→
×
p
→
{\displaystyle {\vec {l}}={\vec {r}}\times {\vec {p}}\,}
L
t
o
t
a
l
=
I
ω
.
{\displaystyle L_{total}=I\omega .}
▭ Precession of a top
ω
P
=
m
r
g
/
(
I
ω
)
.
{\displaystyle \omega _{P}=mrg/(I\omega ).}
▭ (Young's , Bulk , Shear ) modulus:
(
F
⊥
A
=
Y
⋅
Δ
L
L
0
,
Δ
p
=
B
⋅
−
Δ
V
V
0
,
F
∥
A
=
S
⋅
Δ
x
L
0
)
{\displaystyle \left({\tfrac {F_{\perp }}{A}}=Y\cdot {\tfrac {\Delta L}{L_{0}}}\,,\;\Delta p=B\cdot {\tfrac {-\Delta V}{V_{0}}}\,,\;{\tfrac {F_{\parallel }}{A}}=S\cdot {\tfrac {\Delta x}{L_{0}}}\right)}
Newton's law of gravity
F
→
12
=
G
m
1
m
2
r
2
r
^
12
{\displaystyle {\vec {F}}_{12}=G{\tfrac {m_{1}m_{2}}{r^{2}}}{\hat {r}}_{12}}
▭ Earth's gravity
g
=
G
M
E
r
2
{\displaystyle g=G{\tfrac {M_{E}}{r^{2}}}}
▭ Gravitational PE beyond Earth
U
=
−
G
M
E
m
r
{\displaystyle U=-G{\tfrac {M_{E}m}{r}}}
▭ Energy conservation
1
2
m
v
1
2
−
G
M
m
r
1
=
1
2
m
v
2
2
−
G
M
m
r
2
{\displaystyle {\tfrac {1}{2}}mv_{1}^{2}-G{\tfrac {Mm}{r_{1}}}={\tfrac {1}{2}}mv_{2}^{2}-G{\tfrac {Mm}{r_{2}}}}
▭ Escape velocity
v
e
s
c
=
2
G
M
E
r
{\displaystyle v_{esc}={\sqrt {\tfrac {2GM_{E}}{r}}}}
▭ Orbital speed
v
o
r
b
i
t
=
G
M
E
r
{\displaystyle v_{orbit}={\sqrt {\tfrac {GM_{E}}{r}}}}
▭ Orbital period
T
=
2
π
r
3
G
M
E
{\displaystyle T=2\pi {\sqrt {\tfrac {r^{3}}{GM_{E}}}}}
▭ Energy in circular orbit
E
=
K
+
U
=
−
G
m
M
E
2
r
{\displaystyle E=K+U=-{\tfrac {GmM_{E}}{2r}}}
▭ Conic section
α
r
=
1
+
e
cos
θ
{\displaystyle {\tfrac {\alpha }{r}}=1+e\,\!\cos \theta }
▭ Kepler's third law
T
2
=
4
π
2
G
M
a
3
{\displaystyle T^{2}={\tfrac {4\pi ^{2}}{GM}}a^{3}}
▭ Schwarzschild radius
R
S
=
2
G
M
c
2
{\displaystyle R_{S}={\tfrac {2GM}{c^{2}}}}
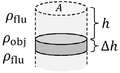
Pressure is the weight per unit area of the fluid above a point. The buoyant force
B
{\displaystyle B}
W
{\displaystyle W}
A
Δ
h
{\displaystyle A\Delta h}
▭
B
=
ρ
f
l
u
(
A
Δ
h
)
g
{\displaystyle B=\rho _{flu}(A\Delta h)g}
W
=
ρ
o
b
j
(
A
Δ
h
)
g
=
M
o
b
j
g
{\displaystyle W=\rho _{obj}(A\Delta h)g=M_{obj}g}
▭ Pressure vs depth/height (constant density)
p
=
p
o
+
ρ
g
h
⇐
d
p
/
d
y
=
−
ρ
g
{\displaystyle \,p=p_{o}+\rho gh\Leftarrow dp/dy=-\rho g}
▭ Absolute vs gauge pressure
p
a
b
s
=
p
g
+
p
a
t
m
{\displaystyle \,p_{abs}=p_{g}+p_{atm}\;}
▭ Pascal's principle :
F
/
A
{\displaystyle \,F/A\,}
A .
▭ Volume flow rate
Q
=
d
V
/
d
t
{\displaystyle Q=dV/dt\;}
▭ Continuity equation
ρ
1
A
1
v
1
=
ρ
2
A
2
v
2
{\displaystyle \rho _{1}A_{1}v_{1}=\rho _{2}A_{2}v_{2}}
⇒
A
1
v
1
=
A
2
v
2
if
ρ
=
c
o
n
s
t
.
{\displaystyle \Rightarrow A_{1}v_{1}=A_{2}v_{2}{\text{ if }}\rho =const.\;}
▭ Bernoulli's principle
p
1
+
1
2
ρ
v
1
2
+
ρ
g
y
1
=
p
2
+
1
2
ρ
v
2
2
+
ρ
g
y
2
{\displaystyle p_{1}+{\tfrac {1}{2}}\rho v_{1}^{2}+\rho gy_{1}=p_{2}+{\tfrac {1}{2}}\rho v_{2}^{2}+\rho gy_{2}}
▭ Viscosity
η
=
F
L
v
A
{\displaystyle \eta ={\tfrac {FL}{vA}}}
▭ Poiseuille equation
p
2
−
p
1
=
Q
R
{\displaystyle p_{2}-p_{1}=QR}
R
=
8
η
ℓ
π
r
4
{\displaystyle R={\tfrac {8\eta \ell }{\pi r^{4}}}}
r
{\displaystyle r}
ℓ
{\displaystyle \ell }
▭ Simple harmonic motion
x
(
t
)
=
A
cos
(
ω
t
+
ϕ
)
,
{\displaystyle x(t)=A\cos(\omega t+\phi ),\,}
v
(
t
)
=
−
A
ω
sin
(
ω
t
+
ϕ
)
,
{\displaystyle v(t)=-A\omega \sin(\omega t+\phi ),\,}
a
(
t
)
=
−
A
ω
2
cos
(
ω
t
+
ϕ
)
{\displaystyle a(t)=-A\omega ^{2}\cos(\omega t+\phi )}
models the x-component of uniform circular motion.
▭ For
(
A
,
ω
)
{\displaystyle (A,\omega )}
x
m
a
x
=
A
,
v
m
a
x
=
A
ω
,
a
m
a
x
=
A
ω
2
{\displaystyle \,x_{max}=A,\;v_{max}=A\omega ,\;a_{max}=A\omega ^{2}}
▭ Mass-spring
ω
=
2
π
/
T
=
2
π
f
=
k
/
m
;
{\displaystyle \omega =2\pi /T=2\pi f={\sqrt {k/m}};\,}
▭ Energy
E
T
o
t
=
1
2
k
x
2
+
1
2
m
v
2
=
1
2
m
v
m
a
x
2
=
1
2
k
x
m
a
x
2
⇒
{\displaystyle E_{Tot}={\tfrac {1}{2}}kx^{2}+{\tfrac {1}{2}}mv^{2}={\tfrac {1}{2}}mv_{max}^{2}={\tfrac {1}{2}}kx_{max}^{2}\Rightarrow }
v
=
±
k
m
(
A
2
−
x
2
)
{\displaystyle v=\pm {\sqrt {{\tfrac {k}{m}}\left(A^{2}-x^{2}\right)}}}
▭ Simple pendulum
ω
≈
g
/
L
{\displaystyle \omega \approx {\sqrt {g/L}}}
▭ Physical pendulum
τ
=
−
M
g
L
sin
θ
≈
−
M
g
L
θ
⇒
{\displaystyle \tau =-MgL\sin \theta \approx -MgL\theta \Rightarrow \;}
ω
=
m
g
L
/
I
{\displaystyle \omega ={\sqrt {mgL/I}}}
L
{\displaystyle L}
CM .
▭ Torsional pendulum
τ
=
−
κ
θ
{\displaystyle \tau =-\kappa \theta }
⇒
ω
=
I
/
κ
{\displaystyle \Rightarrow \omega ={\sqrt {I/\kappa }}}
▭ Damped harmonic oscillator
m
d
2
x
d
t
2
=
−
k
x
−
b
d
x
d
t
{\displaystyle m{\tfrac {d^{2}x}{dt^{2}}}=-kx-b{\tfrac {dx}{dt}}}
⇒
x
=
A
0
e
b
2
m
t
cos
(
ω
t
+
ϕ
)
{\displaystyle \Rightarrow x=A_{0}e^{{\frac {b}{2m}}t}\cos {(\omega t+\phi )}}
ω
=
ω
0
2
−
(
b
2
m
)
2
{\displaystyle \omega ={\sqrt {\omega _{0}^{2}-\left({\tfrac {b}{2m}}\right)^{2}}}}
ω
0
=
k
m
.
{\displaystyle \omega _{0}={\sqrt {\tfrac {k}{m}}}.}
▭ Forced harmonic oscillator (MIT wiki! )
m
d
2
x
d
t
2
=
−
k
x
−
b
d
x
d
t
+
F
0
sin
ω
t
{\displaystyle m{\tfrac {d^{2}x}{dt^{2}}}=-kx-b{\tfrac {dx}{dt}}+F_{0}\sin \omega t}
⇒
x
=
A
e
b
2
m
t
cos
(
ω
t
+
ϕ
)
{\displaystyle \Rightarrow x=Ae^{{\frac {b}{2m}}t}\cos {(\omega t+\phi )}}
A
=
F
0
m
2
(
ω
−
ω
0
)
2
+
b
2
ω
2
{\displaystyle A={\tfrac {F_{0}}{\sqrt {m^{2}(\omega -\omega _{0})^{2}+b^{2}\omega ^{2}}}}}
▭ Wave and pulse speed of a stretched string
=
F
T
/
μ
{\displaystyle ={\sqrt {F_{T}/\mu }}}
F
T
{\displaystyle F_{T}}
tension and
μ
{\displaystyle \mu }
linear mass density .
▭ Speed of a compression wave in a fluid
v
=
B
/
ρ
.
{\displaystyle v={\sqrt {B/\rho }}.}
▭ Periodic travelling wave
y
(
x
,
t
)
=
A
sin
(
k
x
∓
ω
t
)
{\displaystyle y(x,t)=A\sin(kx\mp \omega t)}
k
x
∓
ω
t
{\displaystyle kx\mp \omega t}
A
{\displaystyle A}
▭ The resultant of two waves with identical amplitude and frequency
y
R
(
x
,
t
)
=
[
2
A
cos
(
ϕ
2
)
]
sin
(
k
x
−
ω
t
+
ϕ
2
)
{\displaystyle y_{R}(x,t)=\left[2A\cos \left({\tfrac {\phi }{2}}\right)\right]\sin \left(kx-\omega t+{\tfrac {\phi }{2}}\right)}
ϕ
{\displaystyle \phi }
phase shift .
▭ This wave equation
∂
2
y
/
∂
t
2
=
v
w
2
∂
2
y
/
∂
x
2
{\displaystyle \partial ^{2}y/\partial t^{2}=v_{w}^{2}\,\partial ^{2}y/\partial x^{2}}
linear in
y
=
y
(
x
,
t
)
{\displaystyle y=y(x,t)}
▭ Power in a tranverse stretched string wave
P
a
v
e
=
1
2
μ
A
2
ω
2
v
{\displaystyle P_{ave}={\tfrac {1}{2}}\mu A^{2}\omega ^{2}v}
▭ Intensity of a plane wave
I
=
P
/
A
⇒
P
4
π
r
2
{\displaystyle I=P/A\Rightarrow {\tfrac {P}{4\pi r^{2}}}}
spherical wave .
▭ Standing wave
y
(
x
,
t
)
=
A
sin
(
k
x
)
cos
(
ω
t
+
ϕ
)
{\displaystyle y(x,t)=A\sin(kx)\cos(\omega t+\phi )}
boundary conditions
λ
n
=
2
π
/
k
n
=
2
π
L
{\displaystyle \lambda _{n}=2\pi /k_{n}={\tfrac {2}{\pi }}L}
n
=
1
,
2
,
3
,
.
.
.
{\displaystyle n=1,2,3,...}
f
=
n
f
1
{\displaystyle f=nf_{1}}
f
1
=
v
2
L
{\displaystyle f_{1}={\tfrac {v}{2L}}}
fundamental frequency .
Pressure and displacement fluctuations in a sound wave
P
=
Δ
P
m
a
x
sin
(
k
x
∓
ω
t
+
ϕ
)
{\displaystyle P=\Delta P_{max}\sin(kx\mp \omega t+\phi )}
s
=
s
m
a
x
cos
(
k
x
∓
ω
t
+
ϕ
)
{\displaystyle s=s_{max}\cos(kx\mp \omega t+\phi )}
▭ Speed of sound in a fluid
v
=
f
λ
=
β
/
ρ
{\displaystyle v=f\lambda ={\sqrt {\beta /\rho }}}
Y
/
ρ
{\displaystyle {\sqrt {Y/\rho }}}
γ
R
T
/
M
{\displaystyle {\sqrt {\gamma RT/M}}}
331
m
s
T
K
273
K
=
331
m
s
1
+
T
C
273
o
C
{\displaystyle 331{\tfrac {m}{s}}{\sqrt {\tfrac {T_{K}}{273\,K}}}=331{\tfrac {m}{s}}{\sqrt {1+{\tfrac {T_{C}}{273^{o}C}}}}}
▭ Decreasing intensity spherical wave
I
2
=
I
1
(
r
1
r
2
)
2
{\displaystyle I_{2}=I_{1}\left({\tfrac {r_{1}}{r_{2}}}\right)^{2}}
▭ Sound intensity
I
=
⟨
P
⟩
A
=
(
Δ
P
m
a
x
)
2
2
ρ
v
{\displaystyle I={\tfrac {\langle P\rangle }{A}}={\tfrac {\left(\Delta P_{max}\right)^{2}}{2\rho v}}}
10
log
10
I
/
I
0
{\displaystyle 10\log _{10}{I/I_{0}}}
▭ Resonance tube One end closed:
λ
n
=
4
n
L
,
{\displaystyle \lambda _{n}={\tfrac {4}{n}}L,}
f
n
=
n
v
4
L
,
{\displaystyle f_{n}=n{\tfrac {v}{4L}},}
n
=
1
,
3
,
5
,
.
.
.
{\displaystyle n=1,3,5,...}
λ
n
=
2
n
L
,
{\displaystyle \lambda _{n}={\tfrac {2}{n}}L,}
f
n
=
n
v
2
L
,
{\displaystyle f_{n}=n{\tfrac {v}{2L}},}
n
=
1
,
2
,
3
,
.
.
.
{\displaystyle n=1,2,3,...}
▭ Beat frequency
f
b
e
a
t
=
|
f
2
−
f
1
|
{\displaystyle f_{beat}=|f_{2}-f_{1}|}
nonrelativistic ) Doppler effect
f
o
=
f
s
v
±
v
o
v
∓
v
s
{\displaystyle f_{o}=f_{s}{\tfrac {v\pm v_{o}}{v\mp v_{s}}}}
v
{\displaystyle v}
v
s
{\displaystyle v_{s}}
v
o
{\displaystyle v_{o}}
▭ Angle of shock wave
sin
θ
=
v
/
v
s
=
1
/
M
{\displaystyle \sin \theta =v/v_{s}=1/M}
v
{\displaystyle v}
speed of sound ,
v
s
{\displaystyle v_{s}}
M
{\displaystyle M}
Mach number .



























































![{\displaystyle y=(\tan \theta _{0})x-\left[{\tfrac {g}{2(v_{0}\cos \theta _{0})^{2}}}\right]x^{2}\,,\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12c32b4b09920712b8d39704824b2648260bb6d4)




























































































































































![{\displaystyle y_{R}(x,t)=\left[2A\cos \left({\tfrac {\phi }{2}}\right)\right]\sin \left(kx-\omega t+{\tfrac {\phi }{2}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a6862f6831d0a0f45bd98a9b627d1fc16757308)






























