http://cnx.org/content/col12074/latest/
T
C
=
5
9
(
T
F
−
32
)
{\displaystyle T_{C}={\tfrac {5}{9}}\left(T_{F}-32\right)}
relates
Celsius to
Fahrenheit temperature scales .
T
K
=
T
C
+
273.15
{\displaystyle T_{K}=T_{C}+273.15}
relates
Kelvin to Celsius.
▭ Linear thermal expansion :
Δ
L
=
α
L
Δ
T
{\displaystyle \Delta L=\alpha L\Delta T}
L
{\displaystyle L}
α
{\displaystyle \alpha }
coefficient of linear expansion .
Δ
A
=
2
α
A
Δ
T
{\displaystyle \Delta A=2\alpha A\Delta T}
Δ
V
=
β
V
Δ
T
{\displaystyle \Delta V=\beta V\Delta T}
respectively .Heat transfer is
Q
=
m
c
Δ
T
{\displaystyle Q=mc\Delta T}
c
{\displaystyle c}
specific heat capacity . In a calorimeter ,
Q
c
o
l
d
+
Q
h
o
t
=
0
{\displaystyle Q_{cold}+Q_{hot}=0}
Latent heat due to a phase change is
Q
=
m
L
f
{\displaystyle Q=mL_{f}}
Q
=
m
L
v
{\displaystyle Q=mL_{v}}
Heat conduction (power ):
P
=
k
A
(
T
h
−
T
c
)
d
{\displaystyle P={\tfrac {kA(T_{h}-T_{c})}{d}}}
k
{\displaystyle k}
d
{\displaystyle d}
A
{\displaystyle A}
P
n
e
t
=
σ
e
A
(
T
2
4
−
T
1
4
)
{\displaystyle P_{net}=\sigma eA\left(T_{2}^{4}-T_{1}^{4}\right)}
radiative
energy transfer rate where
e
{\displaystyle e}
emissivity and
σ
{\displaystyle \sigma }
Stefan–Boltzmann constant.
▭
N
=
n
N
A
{\displaystyle N=nN_{A}}
Gas constant
R
{\displaystyle R}
8.3 J K −1 /mol Avegadro's number :
N
A
{\displaystyle N_{A}}
6.02×1023 . Boltzmann's constant :
k
B
{\displaystyle k_{B}}
1.38×10−23 J /K .Van der Waals equation
[
p
+
a
(
n
V
)
2
]
(
V
−
n
b
)
=
n
R
T
{\displaystyle \left[p+a(nV)^{2}\right](V-nb)=nRT}
RMS speed
v
r
m
s
=
v
2
¯
=
3
R
T
M
=
3
k
B
T
m
{\displaystyle v_{rms}={\sqrt {\overline {v^{2}}}}={\sqrt {\tfrac {3RT}{M}}}={\sqrt {\tfrac {3k_{B}T}{m}}}}
overline denotes mean ,
m
{\displaystyle m}
M
{\displaystyle M}
molar mass .Mean free path
λ
=
V
4
2
π
r
2
N
=
k
B
T
4
2
π
r
2
p
=
v
r
m
s
τ
{\displaystyle \lambda ={\tfrac {V}{4{\sqrt {2}}\pi r^{2}N}}={\tfrac {k_{B}T}{4{\sqrt {2}}\pi r^{2}p}}=v_{rms}\tau }
τ
{\displaystyle \tau }
mean-free-time Internal energy of an ideal monatomic gas
E
i
n
t
=
3
2
N
k
B
T
=
N
K
¯
{\displaystyle E_{int}={\tfrac {3}{2}}Nk_{B}T=N{\overline {K}}}
K
¯
=
{\displaystyle {\overline {K}}=}
kinetic energy of a particle.
Q
=
n
C
V
Δ
T
{\displaystyle Q=nC_{V}\Delta T}
molar heat capacity at constant volume .
C
V
=
d
2
R
{\displaystyle C_{V}={\tfrac {d}{2}}R}
d
{\displaystyle d}
degrees of freedom Maxwell–Boltzmann speed distribution
f
(
v
)
=
4
π
(
m
2
k
B
T
)
3
/
2
v
2
e
−
m
v
2
/
2
k
B
T
{\displaystyle f(v)={\tfrac {4}{\sqrt {\pi }}}\left({\tfrac {m}{2k_{B}T}}\right)^{3/2}v^{2}e^{-mv^{2}/2k_{B}T}}
v
¯
=
8
π
R
T
M
{\displaystyle {\bar {v}}={\sqrt {{\tfrac {8}{\pi }}{\tfrac {RT}{M}}}}}
Peak velocity
v
p
=
2
R
T
M
{\displaystyle v_{p}={\sqrt {\tfrac {2RT}{M}}}}
▭ Equation of state
f
(
p
,
V
,
T
)
=
0
{\displaystyle f(p,V,T)=0}
Work done by a system
W
=
∫
V
1
V
2
p
d
V
{\displaystyle W=\int _{V_{1}}^{V_{2}}pdV}
Internal energy
E
i
n
t
=
∑
i
(
K
¯
i
+
U
¯
i
)
{\displaystyle E_{int}=\sum _{i}\left({\overline {K}}_{i}+{\overline {U}}_{i}\right)}
First law
Δ
E
i
n
t
=
Q
−
W
{\displaystyle \Delta E_{int}=Q-W}
in and W is work done by as shown in the figure)
C
p
=
C
V
+
R
{\displaystyle C_{p}=C_{V}+R}
heat capacity at constant volume
p
V
γ
=
constant
{\displaystyle pV^{\gamma }={\text{constant}}}
heat capacity ratio
γ
=
C
p
/
C
V
{\displaystyle \gamma =C_{p}/C_{V}}
W
=
Q
h
−
Q
c
=
{\displaystyle W=Q_{h}-Q_{c}=}
heat engine cycle.
▭ Efficiency
=
e
=
W
Q
h
=
1
−
Q
c
Q
h
{\displaystyle =e={\tfrac {W}{Q_{h}}}=1-{\tfrac {Q_{c}}{Q_{h}}}}
▭ Coefficient of performance for a refrigerator
K
R
=
Q
c
W
=
Q
c
Q
h
−
Q
c
{\displaystyle K_{R}={\tfrac {Q_{c}}{W}}={\tfrac {Q_{c}}{Q_{h}-Q_{c}}}}
heat pump
K
P
=
Q
h
W
=
Q
h
Q
h
−
Q
c
{\displaystyle K_{P}={\tfrac {Q_{h}}{W}}={\tfrac {Q_{h}}{Q_{h}-Q_{c}}}}
Entropy change
Δ
S
=
Q
T
{\displaystyle \Delta S={\tfrac {Q}{T}}}
reversible process at constant temperature)
→
∫
A
B
d
Q
T
=
S
B
−
S
A
{\displaystyle \rightarrow \int _{A}^{B}{\tfrac {dQ}{T}}=S_{B}-S_{A}}
∮
d
Q
T
{\displaystyle \oint {\tfrac {dQ}{T}}}
cyclic process
→
∫
A
B
d
Q
T
=
S
B
−
S
A
{\displaystyle \rightarrow \int _{A}^{B}{\tfrac {dQ}{T}}=S_{B}-S_{A}}
path independent .
Δ
S
≥
0
{\displaystyle \Delta S\geq 0}
closed system .
lim
T
→
0
Δ
S
=
0
{\displaystyle \lim _{T\to 0}\Delta S=0}
isothermal process .
Coulomb's Law
F
→
=
1
4
π
ε
0
q
1
q
2
r
12
2
r
^
12
{\displaystyle {\vec {F}}={\tfrac {1}{4\pi \varepsilon _{0}}}{\tfrac {q_{1}q_{2}}{r_{12}^{2}}}{\hat {r}}_{12}}
vacuum permittivity
ε
0
=
{\displaystyle \varepsilon _{0}=}
−12 F /m.
Elementary charge = e = 1.602×10−19 C (electrons have charge q=−e and protons have charge q=+e.)
Dipole moment ▭ By superposition ,
F
→
=
1
4
π
ε
0
Q
∑
i
=
1
N
q
i
r
Q
i
2
r
^
Q
i
{\displaystyle {\vec {F}}={\tfrac {1}{4\pi \varepsilon _{0}}}Q\sum _{i=1}^{N}{\tfrac {q_{i}}{r_{Qi}^{2}}}{\hat {r}}_{Qi}}
r
→
Q
i
=
r
→
Q
−
r
→
i
{\displaystyle {\vec {r}}_{Qi}={\vec {r}}_{Q}-{\vec {r}}_{i}}
Electric field
F
→
=
Q
E
→
{\displaystyle {\vec {F}}=Q{\vec {E}}}
E
→
(
r
→
P
)
=
1
4
π
ε
0
∑
i
=
1
N
q
i
r
P
i
2
r
^
P
i
{\displaystyle {\vec {E}}({\vec {r}}_{P})={\tfrac {1}{4\pi \varepsilon _{0}}}\sum _{i=1}^{N}{\tfrac {q_{i}}{r_{Pi}^{2}}}{\hat {r}}_{Pi}}
r
→
P
{\displaystyle {\vec {r}}_{P}}
r
→
i
{\displaystyle {\vec {r}}_{i}}
infinite wire
E
→
(
z
)
=
1
4
π
ε
0
2
λ
z
k
^
{\displaystyle {\vec {E}}(z)={\tfrac {1}{4\pi \varepsilon _{0}}}{\tfrac {2\lambda }{z}}{\hat {k}}}
infinite plane
E
→
=
σ
2
ε
0
k
^
{\displaystyle {\vec {E}}={\tfrac {\sigma }{2\varepsilon _{0}}}{\hat {k}}}
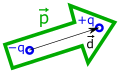
electric dipole
p
→
=
q
d
→
{\displaystyle {\vec {p}}=q{\vec {d}}}
torque
τ
=
p
→
×
E
→
{\displaystyle \tau ={\vec {p}}\times {\vec {E}}}
closed .. open
Flux for a uniform electric field
Φ
=
E
→
⋅
A
→
{\displaystyle \Phi ={\vec {E}}\cdot {\vec {A}}}
→
Φ
=
∫
E
→
⋅
d
A
→
=
∫
E
→
⋅
n
^
d
A
{\displaystyle \to \Phi =\int {\vec {E}}\cdot d{\vec {A}}=\int {\vec {E}}\cdot {\hat {n}}\,dA}
▭ Closed surface integral
Φ
=
∮
E
→
⋅
d
A
→
=
∮
E
→
⋅
n
^
d
A
{\displaystyle \Phi =\oint {\vec {E}}\cdot d{\vec {A}}=\oint {\vec {E}}\cdot {\hat {n}}\,dA}
Gauss's Law
=
q
e
n
c
=
ε
0
∮
E
→
⋅
d
A
→
{\displaystyle =q_{enc}=\varepsilon _{0}\oint {\vec {E}}\cdot d{\vec {A}}}
E
∫
d
A
=
E
A
∗
=
q
e
n
c
ε
0
{\displaystyle E\int dA=EA^{*}={\tfrac {q_{enc}}{\varepsilon _{0}}}}
E
→
=
σ
ε
0
{\displaystyle {\vec {E}}={\tfrac {\sigma }{\varepsilon _{0}}}}
Electric potential
Δ
V
A
B
=
V
A
−
V
B
=
−
∫
A
B
E
→
⋅
d
ℓ
→
{\displaystyle \Delta V_{AB}=V_{A}-V_{B}=-\int _{A}^{B}{\vec {E}}\cdot d{\vec {\ell }}}
potential energy
=
q
Δ
V
=
Δ
U
{\displaystyle =q\Delta V=\Delta U}
▭ Electron (proton) mass = 9.11×10−31 kg (1.67× 10−27 kg). Electron volt: 1 eV = 1.602×10−19 J point charge
V
(
r
)
=
k
q
r
{\displaystyle V(r)=k{\tfrac {q}{r}}}
k
=
1
4
π
ε
0
{\displaystyle k={\tfrac {1}{4\pi \varepsilon _{0}}}}
9 N ·m /C 2 is the Coulomb constant .Work done to assemble N particles
W
12...
N
=
∑
i
=
1
N
∑
j
=
1
i
−
1
q
i
q
j
r
i
j
=
k
2
∑
i
=
1
N
∑
j
=
1
N
q
i
q
j
r
i
j
for
i
≠
j
{\displaystyle W_{12...N}=\sum _{i=1}^{N}\sum _{j=1}^{i-1}{\tfrac {q_{i}q_{j}}{r_{ij}}}={\tfrac {k}{2}}\sum _{i=1}^{N}\sum _{j=1}^{N}{\tfrac {q_{i}q_{j}}{r_{ij}}}{\text{ for }}i\neq j}
V
P
=
k
∑
1
N
q
i
r
i
{\displaystyle V_{P}=k\sum _{1}^{N}{\frac {q_{i}}{r_{i}}}}
continuous charge
V
P
=
k
∫
d
q
r
{\displaystyle V_{P}=k\int {\frac {dq}{r}}}
dipole ,
V
=
k
p
→
⋅
r
^
→
r
2
{\displaystyle V=k{\tfrac {{\vec {p}}\cdot {\vec {\hat {r}}}}{r^{2}}}}
Electric field as gradient of potential
E
→
=
−
∂
V
∂
x
i
^
−
∂
V
∂
y
j
^
−
∂
V
∂
z
k
^
=
−
∇
→
V
{\displaystyle {\vec {E}}=-{\tfrac {\partial V}{\partial x}}{\hat {i}}-{\tfrac {\partial V}{\partial y}}{\hat {j}}-{\tfrac {\partial V}{\partial z}}{\hat {k}}=-{\vec {\nabla }}V}
Del operator note Cartesian
∇
→
=
i
^
∂
∂
x
+
j
^
∂
∂
y
+
k
^
∂
∂
z
;
{\displaystyle {\vec {\nabla }}={\hat {i}}{\tfrac {\partial }{\partial x}}+{\hat {j}}{\tfrac {\partial }{\partial y}}+{\hat {k}}{\tfrac {\partial }{\partial z}}{\text{; }}}
Cylindrical
∇
→
=
r
^
∂
∂
r
+
ϕ
^
∂
∂
ϕ
+
z
^
∂
∂
z
;
{\displaystyle {\vec {\nabla }}={\hat {r}}{\tfrac {\partial }{\partial r}}+{\hat {\phi }}{\tfrac {\partial }{\partial \phi }}+{\hat {z}}{\tfrac {\partial }{\partial z}}{\text{; }}}
∇
→
=
r
^
∂
∂
r
+
θ
^
∂
∂
θ
+
ϕ
^
∂
∂
ϕ
.
{\displaystyle {\vec {\nabla }}={\hat {r}}{\tfrac {\partial }{\partial r}}+{\hat {\theta }}{\tfrac {\partial }{\partial \theta }}+{\hat {\phi }}{\tfrac {\partial }{\partial \phi }}{\text{.}}}
Q
=
C
V
{\displaystyle Q=CV}
capacitance . For a parallel plate capacitor ,
C
=
ε
0
A
d
{\displaystyle C=\varepsilon _{0}{\tfrac {A}{d}}}
▭
4
π
ε
0
R
1
R
2
R
2
−
R
1
{\displaystyle 4\pi \varepsilon _{0}{\tfrac {R_{1}R_{2}}{R_{2}-R_{1}}}}
2
π
ε
0
ℓ
ln
(
R
2
/
R
1
)
{\displaystyle {\tfrac {2\pi \varepsilon _{0}\ell }{\ln(R_{2}/R_{1})}}}
respectively series (parallel)
1
C
S
=
∑
1
C
i
(
C
P
=
∑
C
i
)
{\displaystyle {\tfrac {1}{C_{S}}}=\sum {\tfrac {1}{C_{i}}}\left(C_{P}=\sum C_{i}\right)}
u
=
1
2
Q
V
=
1
2
C
V
2
=
1
2
C
Q
2
{\displaystyle u={\tfrac {1}{2}}QV={\tfrac {1}{2}}CV^{2}={\tfrac {1}{2C}}Q^{2}}
Stored energy density
u
E
=
1
2
ε
0
E
2
{\displaystyle u_{E}={\tfrac {1}{2}}\varepsilon _{0}E^{2}}
dielectric with
κ
>
1
{\displaystyle \kappa >1}
E
=
1
κ
E
0
{\displaystyle E={\tfrac {1}{\kappa }}E_{0}}
U
=
1
κ
U
0
{\displaystyle U={\tfrac {1}{\kappa }}U_{0}}
C
=
κ
C
0
{\displaystyle C=\kappa C_{0}}
E
→
i
=
(
1
κ
−
1
)
E
→
0
{\displaystyle {\vec {E}}_{i}=\left({\tfrac {1}{\kappa }}-1\right){\vec {E}}_{0}}
Current (1A =1C /s )
I
=
d
Q
/
d
t
=
n
q
v
d
A
{\displaystyle I=dQ/dt=nqv_{d}A}
(
n
,
q
,
v
d
)
=
{\displaystyle (n,q,v_{d})=}
density , charge, drift velocity ) of the carriers.
▭
I
=
J
A
→
∫
J
→
⋅
d
A
→
{\displaystyle I=JA\rightarrow \int {\vec {J}}\cdot d{\vec {A}}}
A
{\displaystyle A}
J
{\displaystyle J}
current density .
E
→
=
ρ
J
→
{\displaystyle {\vec {E}}=\rho {\vec {J}}}
electric field , where
ρ
{\displaystyle \rho }
resistivity .Resistivity varies with temperature as
ρ
=
ρ
0
[
1
+
α
(
T
−
T
0
)
]
{\displaystyle \rho =\rho _{0}\left[1+\alpha (T-T_{0})\right]}
R
=
R
0
[
1
+
α
Δ
T
]
{\displaystyle R=R_{0}\left[1+\alpha \Delta T\right]}
R
=
ρ
L
A
{\displaystyle R=\rho {\tfrac {L}{A}}}
resistance (Ω )Ohm's law
V
=
I
R
{\displaystyle V=IR}
Power
=
P
=
I
V
=
I
2
R
=
V
2
/
R
{\displaystyle =P=IV=I^{2}R=V^{2}/R}
▭
V
t
e
r
m
i
n
a
l
s
e
r
i
e
s
=
∑
i
=
1
N
ε
i
−
I
∑
i
=
1
N
r
i
{\displaystyle V_{terminal}^{series}=\sum _{i=1}^{N}\varepsilon _{i}-I\sum _{i=1}^{N}r_{i}}
V
t
e
r
m
i
n
a
l
p
a
r
a
l
l
e
l
=
ε
−
I
∑
i
=
1
N
(
1
r
i
)
−
1
{\displaystyle V_{terminal}^{parallel}=\varepsilon -I\sum _{i=1}^{N}\left({\frac {1}{r_{i}}}\right)^{-1}}
r
i
{\displaystyle r_{i}}
internal resistance of each voltage source .RC (resistor-capacitor) circuit:
q
(
t
)
=
Q
(
1
−
e
−
t
/
τ
)
{\displaystyle q(t)=Q\left(1-e^{-t/\tau }\right)}
I
=
I
0
e
−
t
/
τ
{\displaystyle I=I_{0}e^{-t/\tau }}
τ
=
R
C
{\displaystyle \tau =RC}
RC time,
Q
=
ε
C
{\displaystyle Q=\varepsilon C}
I
0
=
ε
/
R
{\displaystyle I_{0}=\varepsilon /R}
q
(
t
)
=
Q
e
−
t
/
τ
{\displaystyle q(t)=Qe^{-t/\tau }}
I
(
t
)
=
−
Q
R
C
e
−
t
/
τ
{\displaystyle I(t)=-{\tfrac {Q}{RC}}e^{-t/\tau }}
▭
F
→
=
q
v
→
×
B
→
{\displaystyle {\vec {F}}=q{\vec {v}}\times {\vec {B}}}
force due to a magnetic field on a moving charge. current element oriented along
d
ℓ
→
,
d
F
→
=
I
d
ℓ
→
×
B
→
{\displaystyle {\overrightarrow {d\ell }},\;d{\vec {F}}=I{\overrightarrow {d\ell }}\times {\vec {B}}}
▭ The SI unit for magnetic field is the Tesla : 1T=104 Gauss .Gyroradius
r
=
m
B
q
B
.
{\displaystyle r={\tfrac {mB}{qB}}.\;}
Period
T
=
2
π
m
q
B
.
{\displaystyle T={\tfrac {2\pi m}{qB}}.\;}
Torque on current loop
τ
→
=
μ
→
×
B
→
{\displaystyle {\vec {\tau }}={\vec {\mu }}\times {\vec {B}}}
μ
→
=
N
I
A
n
^
{\displaystyle {\vec {\mu }}=NIA{\hat {n}}}
dipole moment . Stored energy
U
=
μ
→
⋅
B
→
.
{\displaystyle U={\vec {\mu }}\cdot {\vec {B}}.}
Drift velocity in crossed electric and magnetic fields
v
d
=
E
B
{\displaystyle v_{d}={\tfrac {E}{B}}}
Hall voltage =
V
{\displaystyle V}
E
=
V
/
ℓ
=
B
v
d
=
I
B
n
e
A
{\displaystyle E=V/\ell =Bv_{d}={\tfrac {IB}{neA}}}
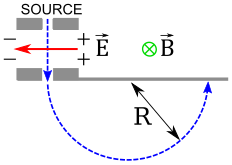
Charge-to-mass ratio
q
/
m
=
E
B
B
0
r
{\displaystyle q/m={\tfrac {E}{BB_{0}r}}}
E
{\displaystyle E}
B
{\displaystyle B}
E
=
0
{\displaystyle E=0}
B
0
{\displaystyle B_{0}}
▭ The magnetic field inside a solenoid filled with paramagnetic material is
B
=
μ
n
I
{\displaystyle B=\mu nI}
μ
=
(
1
+
χ
)
μ
0
{\displaystyle \mu =(1+\chi )\mu _{0}}
permeability
Magnetic flux
Φ
m
=
∫
S
B
→
⋅
n
^
d
A
{\displaystyle \Phi _{m}=\int _{S}{\vec {B}}\cdot {\hat {n}}dA}
Electromotive force
ε
=
−
N
d
Φ
m
d
t
,
{\displaystyle \varepsilon =-N{\tfrac {d\Phi _{m}}{dt,}}}
Faraday's law )Motional emf
ε
=
B
ℓ
v
,
{\displaystyle \varepsilon =B\ell v,}
rotating coil
N
B
A
ω
sin
ω
t
{\displaystyle NBA\omega \sin \omega t}
ε
=
∮
E
→
⋅
d
ℓ
→
=
−
d
Φ
m
d
t
{\displaystyle \varepsilon =\oint {\vec {E}}\cdot d{\vec {\ell }}=-{\tfrac {d\Phi _{m}}{dt}}}
▭ Self-inductance
N
Φ
m
=
L
I
→
ε
=
−
L
d
I
d
t
{\displaystyle N\Phi _{m}=LI\rightarrow \varepsilon =-L{\tfrac {dI}{dt}}}
L
solenoid
≈
μ
0
N
2
A
ℓ
,
{\displaystyle L_{\text{solenoid}}\approx \mu _{0}N^{2}A\ell ,\,}
L
toroid
≈
μ
0
N
2
h
2
π
ln
R
2
R
1
.
{\displaystyle L_{\text{toroid}}\approx {\tfrac {\mu _{0}N^{2}h}{2\pi }}\ln {\tfrac {R_{2}}{R_{1}}}.}
U
=
1
2
L
I
2
.
{\displaystyle U={\tfrac {1}{2}}LI^{2}.}
I
(
t
)
=
ε
R
(
1
−
e
−
t
/
τ
)
{\displaystyle I(t)={\tfrac {\varepsilon }{R}}\left(1-e^{-t/\tau }\right)}
LR circuit where
τ
=
L
/
R
{\displaystyle \tau =L/R}
LR decay time .LC circuit
q
=
q
0
cos
(
ω
t
+
ϕ
)
{\displaystyle q=q_{0}\cos(\omega t+\phi )}
ω
=
1
L
C
{\displaystyle \omega ={\sqrt {\tfrac {1}{LC}}}}
angular frequency LRC circuit
q
(
t
)
=
q
0
e
−
R
t
/
2
L
cos
(
ω
′
t
+
ϕ
)
{\displaystyle q(t)=q_{0}e^{-Rt/2L}\cos(\omega 't+\phi )}
ω
′
=
1
L
C
+
(
R
2
L
)
2
{\displaystyle \omega '={\sqrt {{\tfrac {1}{LC}}+\left({\tfrac {R}{2L}}\right)^{2}}}}
▭ Resistor
V
0
=
I
0
X
R
,
ϕ
=
0
,
{\displaystyle V_{0}=I_{0}X_{R},\;\phi =0,}
X
R
=
R
{\displaystyle X_{R}=R}
Capacitor
V
0
=
I
0
X
C
,
ϕ
=
−
π
2
,
{\displaystyle V_{0}=I_{0}X_{C},\;\phi =-{\tfrac {\pi }{2}},}
X
C
=
1
ω
C
{\displaystyle X_{C}={\tfrac {1}{\omega C}}}
Inductor
V
0
=
I
0
X
L
,
ϕ
=
+
π
2
,
{\displaystyle V_{0}=I_{0}X_{L},\;\phi =+{\tfrac {\pi }{2}},}
X
L
=
ω
L
{\displaystyle X_{L}=\omega L}
RLC series circuit
V
0
=
I
0
Z
{\displaystyle V_{0}=I_{0}Z}
Z
=
R
2
+
(
X
L
−
X
C
)
2
{\displaystyle Z={\sqrt {R^{2}+\left(X_{L}-X_{C}\right)^{2}}}}
ϕ
=
tan
−
1
X
L
−
X
C
R
{\displaystyle \phi =\tan ^{-1}{\frac {X_{L}-X_{C}}{R}}}
Resonant angular frequency
ω
0
=
1
L
C
{\displaystyle \omega _{0}={\sqrt {\tfrac {1}{LC}}}}
Quality factor
Q
=
ω
0
Δ
ω
=
ω
0
L
R
{\displaystyle Q={\tfrac {\omega _{0}}{\Delta \omega }}={\tfrac {\omega _{0}L}{R}}}
Average power
P
a
v
e
=
1
2
I
0
V
0
cos
ϕ
=
I
r
m
s
V
r
m
s
cos
ϕ
{\displaystyle P_{ave}={\frac {1}{2}}I_{0}V_{0}\cos \phi =I_{rms}V_{rms}\cos \phi }
ϕ
=
0
{\displaystyle \phi =0}
Transformer voltages and currents
V
S
V
P
=
N
S
N
P
=
I
P
I
S
{\displaystyle {\tfrac {V_{S}}{V_{P}}}={\tfrac {N_{S}}{N_{P}}}={\tfrac {I_{P}}{I_{S}}}}
Displacement current
I
d
=
ε
0
d
Φ
E
d
t
{\displaystyle I_{d}=\varepsilon _{0}{\tfrac {d\Phi _{E}}{dt}}}
Φ
E
=
∫
E
→
⋅
d
A
→
{\displaystyle \Phi _{E}=\int {\vec {E}}\cdot d{\vec {A}}}
flux .
Maxwell's equations
∮
S
E
→
⋅
d
A
→
=
1
ϵ
0
Q
i
n
∮
S
B
→
⋅
d
A
→
=
0
∮
C
E
→
⋅
d
ℓ
→
=
−
∫
S
∂
B
→
∂
t
⋅
d
A
→
∮
C
B
→
⋅
d
ℓ
→
=
μ
0
I
+
ϵ
0
μ
0
d
Φ
E
d
t
{\displaystyle {\begin{aligned}\oint _{S}{\vec {E}}\cdot \mathrm {d} {\vec {A}}&={\frac {1}{\epsilon _{0}}}Q_{in}\qquad &\oint _{S}{\vec {B}}\cdot \mathrm {d} {\vec {A}}&=0\\\oint _{C}{\vec {E}}\cdot \mathrm {d} {\vec {\ell }}&=-\int _{S}{\frac {\partial {\vec {B}}}{\partial t}}\cdot \mathrm {d} {\vec {A}}\qquad &\oint _{C}{\vec {B}}\cdot \mathrm {d} {\vec {\ell }}&=\mu _{0}I+\epsilon _{0}\mu _{0}{\frac {\mathrm {d} \Phi _{E}}{\mathrm {d} t}}\end{aligned}}}
http://ethw.org/w/index.php?title=Maxwell%27s_Equations&oldid=157445 Plane EM wave equation
∂
2
E
y
∂
x
2
=
ε
0
μ
0
∂
2
E
y
∂
t
2
{\displaystyle {\frac {\partial ^{2}E_{y}}{\partial x^{2}}}=\varepsilon _{0}\mu _{0}{\frac {\partial ^{2}E_{y}}{\partial t^{2}}}}
c
=
1
ε
0
μ
{\displaystyle c={\tfrac {1}{\sqrt {\varepsilon _{0}\mu }}}}
speed of light
E
0
B
0
=
c
{\displaystyle {\tfrac {E_{0}}{B_{0}}}=c}
Poynting vector
S
→
=
1
μ
0
E
→
×
B
→
{\displaystyle {\vec {S}}={\tfrac {1}{\mu _{0}}}{\vec {E}}\times {\vec {B}}}
energy flux
I
=
S
a
v
e
=
c
ε
0
2
E
0
2
=
c
2
μ
0
B
0
2
=
1
2
μ
0
E
0
B
0
{\displaystyle I=S_{ave}={\tfrac {c\varepsilon _{0}}{2}}E_{0}^{2}={\tfrac {c}{2\mu _{0}}}B_{0}^{2}={\tfrac {1}{2\mu _{0}}}E_{0}B_{0}}
Radiation pressure
p
=
I
/
c
{\displaystyle p=I/c}
p
=
2
I
/
c
{\displaystyle p=2I/c}
































=nRT}](https://wikimedia.org/api/rest_v1/media/math/render/svg/572e43e0899bcb5bbbe05adb502a948b501d12c5)













































































![{\displaystyle \rho =\rho _{0}\left[1+\alpha (T-T_{0})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b63fbf7f93624cb84d99cade118b295c49351ffb)
![{\displaystyle R=R_{0}\left[1+\alpha \Delta T\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f43d434660a8941a886bce1f85d9d027d30d6303)